You are given a root to a binary tree and an integer k. A node of this tree is called great enough if the followings hold:
- Its subtree has at least
knodes. - Its value is greater than the value of at least
knodes in its subtree.
Return the number of nodes in this tree that are great enough.
The node u is in the subtree of the node v, if u == v or v is an ancestor of u.
Example 1:
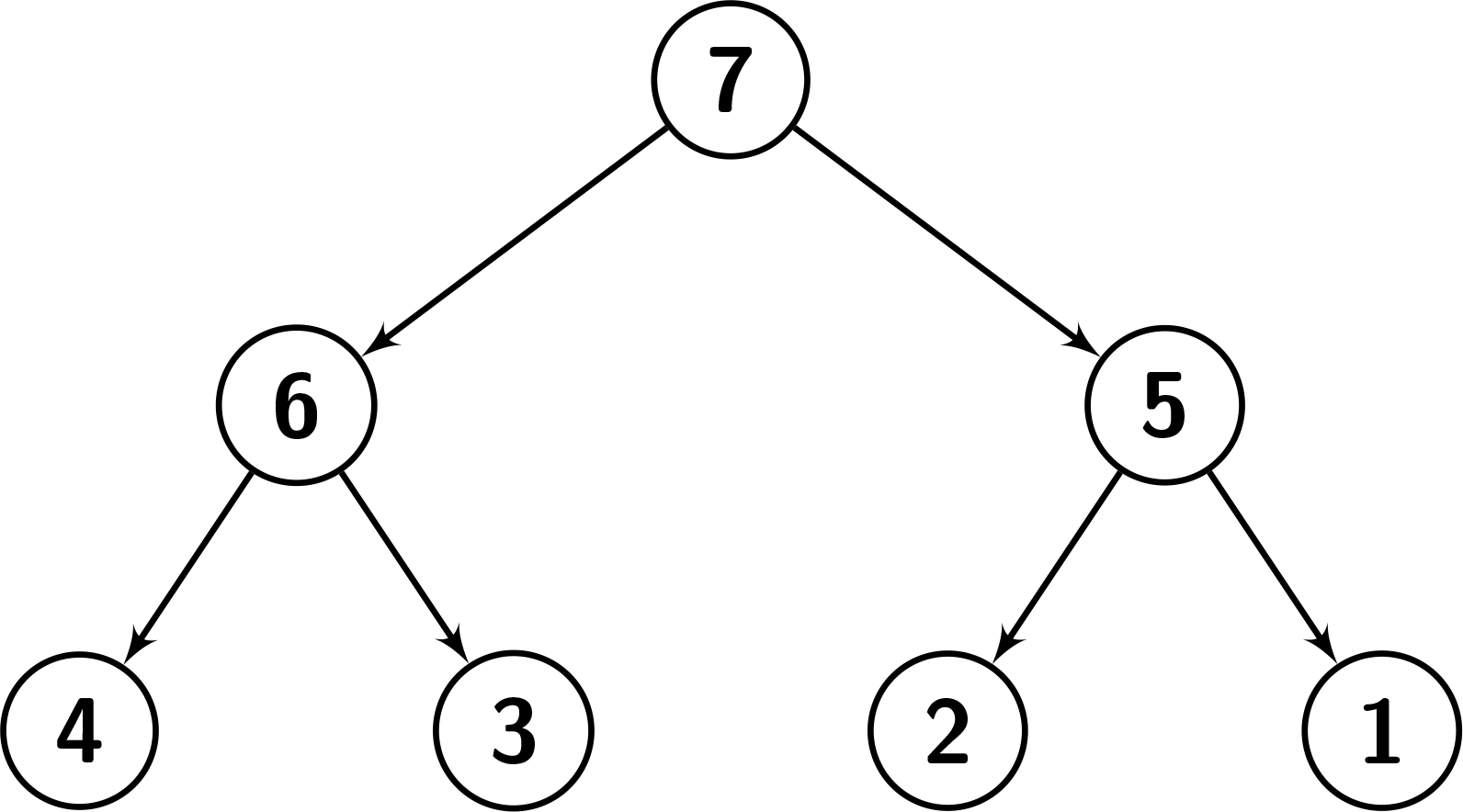
Input: root = [7,6,5,4,3,2,1], k = 2
Output: 3
Explanation: Number the nodes from 1 to 7.
The values in the subtree of node 1: {1,2,3,4,5,6,7}. Since node.val == 7, there are 6 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 2: {3,4,6}. Since node.val == 6, there are 2 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 3: {1,2,5}. Since node.val == 5, there are 2 nodes having a smaller value than its value. So it's great enough.
It can be shown that other nodes are not great enough.
See the picture below for a better understanding.
Example 2:
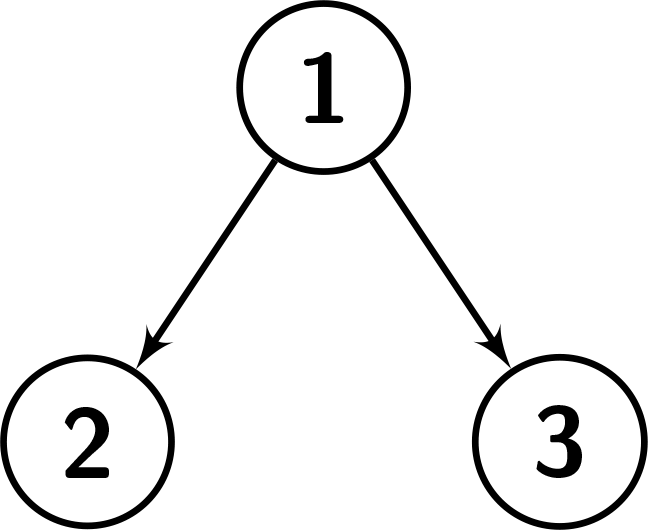
Input: root = [1,2,3], k = 1
Output: 0
Explanation: Number the nodes from 1 to 3.
The values in the subtree of node 1: {1,2,3}. Since node.val == 1, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 2: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 3: {3}. Since node.val == 3, there are no nodes having a smaller value than its value. So it's not great enough.
See the picture below for a better understanding.
Example 3:
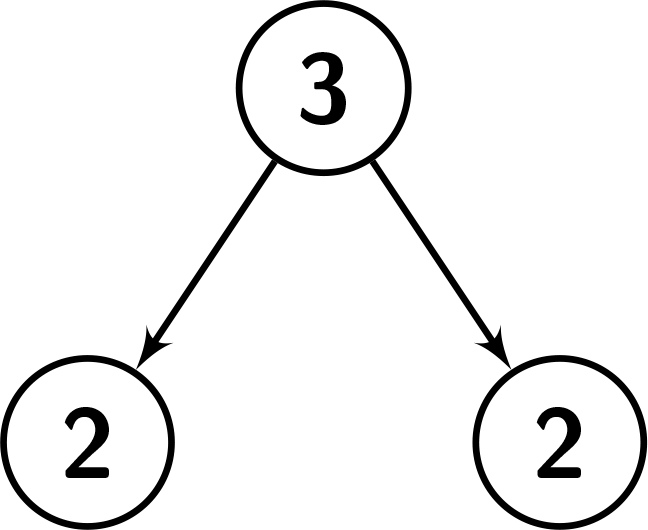
Input: root = [3,2,2], k = 2
Output: 1
Explanation: Number the nodes from 1 to 3.
The values in the subtree of node 1: {2,2,3}. Since node.val == 3, there are 2 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 2: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 3: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
See the picture below for a better understanding.
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 1 <= Node.val <= 1041 <= k <= 10
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countGreatEnoughNodes(self, root: Optional[TreeNode], k: int) -> int:
def push(pq, x):
heappush(pq, x)
if len(pq) > k:
heappop(pq)
def dfs(root):
if root is None:
return []
l, r = dfs(root.left), dfs(root.right)
for x in r:
push(l, x)
if len(l) == k and -l[0] < root.val:
nonlocal ans
ans += 1
push(l, -root.val)
return l
ans = 0
dfs(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
private int k;
public int countGreatEnoughNodes(TreeNode root, int k) {
this.k = k;
dfs(root);
return ans;
}
private PriorityQueue<Integer> dfs(TreeNode root) {
if (root == null) {
return new PriorityQueue<>(Comparator.reverseOrder());
}
var l = dfs(root.left);
var r = dfs(root.right);
for (int x : r) {
l.offer(x);
if (l.size() > k) {
l.poll();
}
}
if (l.size() == k && l.peek() < root.val) {
++ans;
}
l.offer(root.val);
if (l.size() > k) {
l.poll();
}
return l;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countGreatEnoughNodes(TreeNode* root, int k) {
int ans = 0;
function<priority_queue<int>(TreeNode*)> dfs = [&](TreeNode* root) {
if (!root) {
return priority_queue<int>();
}
auto left = dfs(root->left);
auto right = dfs(root->right);
while (right.size()) {
left.push(right.top());
right.pop();
if (left.size() > k) {
left.pop();
}
}
if (left.size() == k && left.top() < root->val) {
++ans;
}
left.push(root->val);
if (left.size() > k) {
left.pop();
}
return left;
};
dfs(root);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func countGreatEnoughNodes(root *TreeNode, k int) (ans int) {
var dfs func(*TreeNode) hp
dfs = func(root *TreeNode) hp {
if root == nil {
return hp{}
}
l, r := dfs(root.Left), dfs(root.Right)
for _, x := range r.IntSlice {
l.push(x)
if l.Len() > k {
l.pop()
}
}
if l.Len() == k && root.Val > l.IntSlice[0] {
ans++
}
l.push(root.Val)
if l.Len() > k {
l.pop()
}
return l
}
dfs(root)
return
}
type hp struct{ sort.IntSlice }
func (h hp) Less(i, j int) bool { return h.IntSlice[i] > h.IntSlice[j] }
func (h *hp) Push(v any) { h.IntSlice = append(h.IntSlice, v.(int)) }
func (h *hp) Pop() any {
a := h.IntSlice
v := a[len(a)-1]
h.IntSlice = a[:len(a)-1]
return v
}
func (h *hp) push(v int) { heap.Push(h, v) }
func (h *hp) pop() int { return heap.Pop(h).(int) }