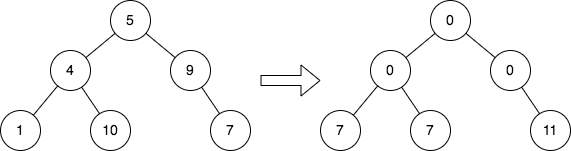
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return the root of the modified tree.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
Input: root = [5,4,9,1,10,null,7] Output: [0,0,0,7,7,null,11] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 5 does not have any cousins so its sum is 0. - Node with value 4 does not have any cousins so its sum is 0. - Node with value 9 does not have any cousins so its sum is 0. - Node with value 1 has a cousin with value 7 so its sum is 7. - Node with value 10 has a cousin with value 7 so its sum is 7. - Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:
Input: root = [3,1,2] Output: [0,0,0] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 3 does not have any cousins so its sum is 0. - Node with value 1 does not have any cousins so its sum is 0. - Node with value 2 does not have any cousins so its sum is 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 104
We create a list
Next, we perform a DFS traversal to calculate the values in the array
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def dfs1(root: Optional[TreeNode], depth: int):
if root is None:
return
if len(s) <= depth:
s.append(0)
s[depth] += root.val
dfs1(root.left, depth + 1)
dfs1(root.right, depth + 1)
def dfs2(root: Optional[TreeNode], depth: int):
sub = (root.left.val if root.left else 0) + (
root.right.val if root.right else 0
)
depth += 1
if root.left:
root.left.val = s[depth] - sub
dfs2(root.left, depth)
if root.right:
root.right.val = s[depth] - sub
dfs2(root.right, depth)
s = []
dfs1(root, 0)
root.val = 0
dfs2(root, 0)
return root/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List<Integer> s = new ArrayList<>();
public TreeNode replaceValueInTree(TreeNode root) {
dfs1(root, 0);
root.val = 0;
dfs2(root, 0);
return root;
}
private void dfs1(TreeNode root, int depth) {
if (root == null) {
return;
}
if (s.size() <= depth) {
s.add(0);
}
s.set(depth, s.get(depth) + root.val);
dfs1(root.left, depth + 1);
dfs1(root.right, depth + 1);
}
private void dfs2(TreeNode root, int depth) {
int l = root.left == null ? 0 : root.left.val;
int r = root.right == null ? 0 : root.right.val;
int sub = l + r;
++depth;
if (root.left != null) {
root.left.val = s.get(depth) - sub;
dfs2(root.left, depth);
}
if (root.right != null) {
root.right.val = s.get(depth) - sub;
dfs2(root.right, depth);
}
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* replaceValueInTree(TreeNode* root) {
memset(s, 0, sizeof(s));
dfs1(root, 0);
root->val = 0;
dfs2(root, 0);
return root;
}
private:
int s[100010];
void dfs1(TreeNode* root, int depth) {
if (!root) {
return;
}
s[depth] += root->val;
dfs1(root->left, depth + 1);
dfs1(root->right, depth + 1);
};
void dfs2(TreeNode* root, int depth) {
int l = root->left ? root->left->val : 0;
int r = root->right ? root->right->val : 0;
int sub = l + r;
++depth;
if (root->left) {
root->left->val = s[depth] - sub;
dfs2(root->left, depth);
}
if (root->right) {
root->right->val = s[depth] - sub;
dfs2(root->right, depth);
}
};
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func replaceValueInTree(root *TreeNode) *TreeNode {
s := []int{}
var dfs1 func(*TreeNode, int)
dfs1 = func(root *TreeNode, depth int) {
if root == nil {
return
}
if len(s) <= depth {
s = append(s, 0)
}
s[depth] += root.Val
dfs1(root.Left, depth+1)
dfs1(root.Right, depth+1)
}
var dfs2 func(*TreeNode, int)
dfs2 = func(root *TreeNode, depth int) {
l, r := 0, 0
if root.Left != nil {
l = root.Left.Val
}
if root.Right != nil {
r = root.Right.Val
}
sub := l + r
depth++
if root.Left != nil {
root.Left.Val = s[depth] - sub
dfs2(root.Left, depth)
}
if root.Right != nil {
root.Right.Val = s[depth] - sub
dfs2(root.Right, depth)
}
}
dfs1(root, 0)
root.Val = 0
dfs2(root, 0)
return root
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function replaceValueInTree(root: TreeNode | null): TreeNode | null {
const s: number[] = [];
const dfs1 = (root: TreeNode | null, depth: number) => {
if (!root) {
return;
}
if (s.length <= depth) {
s.push(0);
}
s[depth] += root.val;
dfs1(root.left, depth + 1);
dfs1(root.right, depth + 1);
};
const dfs2 = (root: TreeNode | null, depth: number) => {
const sub = (root.left?.val || 0) + (root.right?.val || 0);
++depth;
if (root.left) {
root.left.val = s[depth] - sub;
dfs2(root.left, depth);
}
if (root.right) {
root.right.val = s[depth] - sub;
dfs2(root.right, depth);
}
};
dfs1(root, 0);
root.val = 0;
dfs2(root, 0);
return root;
}First, we update the root node's value to
Then, we traverse the queue, calculate the sum
After the traversal ends, we return the root node.
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
root.val = 0
q = [root]
while q:
t = []
s = 0
for node in q:
if node.left:
t.append(node.left)
s += node.left.val
if node.right:
t.append(node.right)
s += node.right.val
for node in q:
sub = (node.left.val if node.left else 0) + (
node.right.val if node.right else 0
)
if node.left:
node.left.val = s - sub
if node.right:
node.right.val = s - sub
q = t
return root/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
root.val = 0;
List<TreeNode> q = List.of(root);
while (!q.isEmpty()) {
List<TreeNode> t = new ArrayList<>();
int s = 0;
for (TreeNode node : q) {
if (node.left != null) {
t.add(node.left);
s += node.left.val;
}
if (node.right != null) {
t.add(node.right);
s += node.right.val;
}
}
for (TreeNode node : q) {
int sub = (node.left == null ? 0 : node.left.val)
+ (node.right == null ? 0 : node.right.val);
if (node.left != null) {
node.left.val = s - sub;
}
if (node.right != null) {
node.right.val = s - sub;
}
}
q = t;
}
return root;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* replaceValueInTree(TreeNode* root) {
root->val = 0;
vector<TreeNode*> q = {root};
while (!q.empty()) {
vector<TreeNode*> t;
int s = 0;
for (TreeNode* node : q) {
if (node->left) {
t.emplace_back(node->left);
s += node->left->val;
}
if (node->right) {
t.emplace_back(node->right);
s += node->right->val;
}
}
for (TreeNode* node : q) {
int sub = (node->left ? node->left->val : 0) + (node->right ? node->right->val : 0);
if (node->left) {
node->left->val = s - sub;
}
if (node->right) {
node->right->val = s - sub;
}
}
q = move(t);
}
return root;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func replaceValueInTree(root *TreeNode) *TreeNode {
root.Val = 0
q := []*TreeNode{root}
for len(q) > 0 {
t := []*TreeNode{}
s := 0
for _, node := range q {
if node.Left != nil {
t = append(t, node.Left)
s += node.Left.Val
}
if node.Right != nil {
t = append(t, node.Right)
s += node.Right.Val
}
}
for _, node := range q {
sub := 0
if node.Left != nil {
sub += node.Left.Val
}
if node.Right != nil {
sub += node.Right.Val
}
if node.Left != nil {
node.Left.Val = s - sub
}
if node.Right != nil {
node.Right.Val = s - sub
}
}
q = t
}
return root
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function replaceValueInTree(root: TreeNode | null): TreeNode | null {
root.val = 0;
const q: TreeNode[] = [root];
while (q.length > 0) {
const t: TreeNode[] = [];
let s = 0;
for (const { left, right } of q) {
if (left) {
t.push(left);
s += left.val;
}
if (right) {
t.push(right);
s += right.val;
}
}
for (const { left, right } of q) {
const sub = (left?.val || 0) + (right?.val || 0);
if (left) {
left.val = s - sub;
}
if (right) {
right.val = s - sub;
}
}
q.splice(0, q.length, ...t);
}
return root;
}