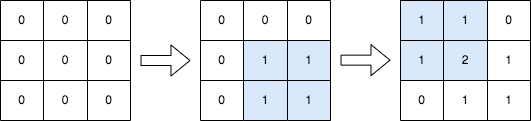
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
- 找出 左上角 为
(row1i, col1i)且 右下角 为(row2i, col2i)的子矩阵,将子矩阵中的 每个元素 加1。也就是给所有满足row1i <= x <= row2i和col1i <= y <= col2i的mat[x][y]加1。
返回执行完所有操作后得到的矩阵 mat 。
示例 1:
输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]] 输出:[[1,1,0],[1,2,1],[0,1,1]] 解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。 - 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。 - 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
示例 2:
输入:n = 2, queries = [[0,0,1,1]] 输出:[[1,1],[1,1]] 解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵。 - 第一个操作:将矩阵中的每个元素加 1 。
提示:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
二维差分模板题。
mat = [[0] * (n + 1) for _ in range(n + 1)]
def insert(x1, y1, x2, y2, c):
mat[x1][y1] += c
mat[x1][y2 + 1] -= c
mat[x2 + 1][y1] -= c
mat[x2 + 1][y2 + 1] += c
for i in range(1, n + 1):
for j in range(1, n + 1):
mat[i][j] += mat[i - 1][j] + mat[i][j - 1] - mat[i - 1][j - 1]时间复杂度 queries 的长度和给定的
class Solution:
def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
mat = [[0] * n for _ in range(n)]
for x1, y1, x2, y2 in queries:
mat[x1][y1] += 1
if x2 + 1 < n:
mat[x2 + 1][y1] -= 1
if y2 + 1 < n:
mat[x1][y2 + 1] -= 1
if x2 + 1 < n and y2 + 1 < n:
mat[x2 + 1][y2 + 1] += 1
for i in range(n):
for j in range(n):
if i:
mat[i][j] += mat[i - 1][j]
if j:
mat[i][j] += mat[i][j - 1]
if i and j:
mat[i][j] -= mat[i - 1][j - 1]
return matclass Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] mat = new int[n][n];
for (var q : queries) {
int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];
mat[x1][y1]++;
if (x2 + 1 < n) {
mat[x2 + 1][y1]--;
}
if (y2 + 1 < n) {
mat[x1][y2 + 1]--;
}
if (x2 + 1 < n && y2 + 1 < n) {
mat[x2 + 1][y2 + 1]++;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i > 0) {
mat[i][j] += mat[i - 1][j];
}
if (j > 0) {
mat[i][j] += mat[i][j - 1];
}
if (i > 0 && j > 0) {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
return mat;
}
}class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> mat(n, vector<int>(n));
for (auto& q : queries) {
int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];
mat[x1][y1]++;
if (x2 + 1 < n) {
mat[x2 + 1][y1]--;
}
if (y2 + 1 < n) {
mat[x1][y2 + 1]--;
}
if (x2 + 1 < n && y2 + 1 < n) {
mat[x2 + 1][y2 + 1]++;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i > 0) {
mat[i][j] += mat[i - 1][j];
}
if (j > 0) {
mat[i][j] += mat[i][j - 1];
}
if (i > 0 && j > 0) {
mat[i][j] -= mat[i - 1][j - 1];
}
}
}
return mat;
}
};func rangeAddQueries(n int, queries [][]int) [][]int {
mat := make([][]int, n)
for i := range mat {
mat[i] = make([]int, n)
}
for _, q := range queries {
x1, y1, x2, y2 := q[0], q[1], q[2], q[3]
mat[x1][y1]++
if x2+1 < n {
mat[x2+1][y1]--
}
if y2+1 < n {
mat[x1][y2+1]--
}
if x2+1 < n && y2+1 < n {
mat[x2+1][y2+1]++
}
}
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if i > 0 {
mat[i][j] += mat[i-1][j]
}
if j > 0 {
mat[i][j] += mat[i][j-1]
}
if i > 0 && j > 0 {
mat[i][j] -= mat[i-1][j-1]
}
}
}
return mat
}