给你一个正整数 n,表示从 1 到 n 的 n 个城市。还给你一个 二维 数组 roads,其中 roads[i] = [ai, bi, costi] 表示在城市 ai 和 bi 之间有一条双向道路,其旅行成本等于 costi。
你可以在 任何 城市买到苹果,但是有些城市买苹果的费用不同。给定数组 appleCost ,其中 appleCost[i] 是从城市 i 购买一个苹果的成本。
你从某个城市开始,穿越各种道路,最终从 任何一个 城市买 一个 苹果。在你买了那个苹果之后,你必须回到你 开始的 城市,但现在所有道路的成本将 乘以 一个给定的因子 k。
给定整数 k,返回一个大小为 n 的数组 answer,其中 answer[i] 是从城市 i 开始购买一个苹果的 最小 总成本。
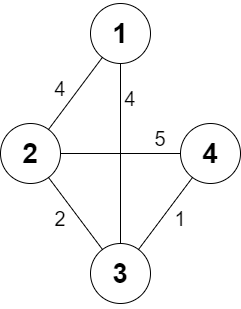
示例 1:
输入: n = 4, roads = [[1,2,4],[2,3,2],[2,4,5],[3,4,1],[1,3,4]], appleCost = [56,42,102,301], k = 2 输出: [54,42,48,51] 解释: 每个起始城市的最低费用如下: - 从城市 1 开始:你走路径 1 -> 2,在城市 2 买一个苹果,最后走路径 2 -> 1。总成本是 4 + 42 + 4 * 2 = 54。 - 从城市 2 开始:你直接在城市 2 买一个苹果。总费用是 42。 - 从城市 3 开始:你走路径 3 -> 2,在城市 2 买一个苹果,最后走路径 2 -> 3。总成本是 2 + 42 + 2 * 2 = 48。 - 从城市 4 开始:你走路径 4 -> 3 -> 2,然后你在城市 2 购买,最后走路径 2 -> 3 -> 4。总成本是 1 + 2 + 42 + 1 * 2 + 2 * 2 = 51。
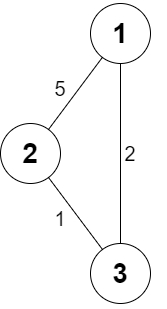
示例 2:
输入: n = 3, roads = [[1,2,5],[2,3,1],[3,1,2]], appleCost = [2,3,1], k = 3 输出: [2,3,1] 解释: 在起始城市买苹果总是最优的。
提示:
2 <= n <= 10001 <= roads.length <= 10001 <= ai, bi <= nai != bi1 <= costi <= 105appleCost.length == n1 <= appleCost[i] <= 1051 <= k <= 100-
没有重复的边。
我们枚举起点,对于每个起点,使用 Dijkstra 算法求出到其他所有点的最短距离,更新最小值即可。
时间复杂度
class Solution:
def minCost(
self, n: int, roads: List[List[int]], appleCost: List[int], k: int
) -> List[int]:
def dijkstra(i):
q = [(0, i)]
dist = [inf] * n
dist[i] = 0
ans = inf
while q:
d, u = heappop(q)
ans = min(ans, appleCost[u] + d * (k + 1))
for v, w in g[u]:
if dist[v] > dist[u] + w:
dist[v] = dist[u] + w
heappush(q, (dist[v], v))
return ans
g = defaultdict(list)
for a, b, c in roads:
a, b = a - 1, b - 1
g[a].append((b, c))
g[b].append((a, c))
return [dijkstra(i) for i in range(n)]class Solution {
private int k;
private int[] cost;
private int[] dist;
private List<int[]>[] g;
private static final int INF = 0x3f3f3f3f;
public long[] minCost(int n, int[][] roads, int[] appleCost, int k) {
cost = appleCost;
g = new List[n];
dist = new int[n];
this.k = k;
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<>();
}
for (var e : roads) {
int a = e[0] - 1, b = e[1] - 1, c = e[2];
g[a].add(new int[] {b, c});
g[b].add(new int[] {a, c});
}
long[] ans = new long[n];
for (int i = 0; i < n; ++i) {
ans[i] = dijkstra(i);
}
return ans;
}
private long dijkstra(int u) {
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
q.offer(new int[] {0, u});
Arrays.fill(dist, INF);
dist[u] = 0;
long ans = Long.MAX_VALUE;
while (!q.isEmpty()) {
var p = q.poll();
int d = p[0];
u = p[1];
ans = Math.min(ans, cost[u] + (long) (k + 1) * d);
for (var ne : g[u]) {
int v = ne[0], w = ne[1];
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.offer(new int[] {dist[v], v});
}
}
}
return ans;
}
}using ll = long long;
using pii = pair<int, int>;
class Solution {
public:
const int inf = 0x3f3f3f3f;
vector<long long> minCost(int n, vector<vector<int>>& roads, vector<int>& appleCost, int k) {
vector<vector<pii>> g(n);
for (auto& e : roads) {
int a = e[0] - 1, b = e[1] - 1, c = e[2];
g[a].push_back({b, c});
g[b].push_back({a, c});
}
int dist[n];
auto dijkstra = [&](int u) {
memset(dist, 63, sizeof dist);
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, u});
dist[u] = 0;
ll ans = LONG_MAX;
while (!q.empty()) {
auto p = q.top();
q.pop();
int d = p.first;
u = p.second;
ans = min(ans, appleCost[u] + 1ll * d * (k + 1));
for (auto& ne : g[u]) {
auto [v, w] = ne;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.push({dist[v], v});
}
}
}
return ans;
};
vector<ll> ans(n);
for (int i = 0; i < n; ++i) ans[i] = dijkstra(i);
return ans;
}
};func minCost(n int, roads [][]int, appleCost []int, k int) []int64 {
g := make([]pairs, n)
for _, e := range roads {
a, b, c := e[0]-1, e[1]-1, e[2]
g[a] = append(g[a], pair{b, c})
g[b] = append(g[b], pair{a, c})
}
const inf int = 0x3f3f3f3f
dist := make([]int, n)
dijkstra := func(u int) int64 {
var ans int64 = math.MaxInt64
for i := range dist {
dist[i] = inf
}
dist[u] = 0
q := make(pairs, 0)
heap.Push(&q, pair{0, u})
for len(q) > 0 {
p := heap.Pop(&q).(pair)
d := p.first
u = p.second
ans = min(ans, int64(appleCost[u]+d*(k+1)))
for _, ne := range g[u] {
v, w := ne.first, ne.second
if dist[v] > dist[u]+w {
dist[v] = dist[u] + w
heap.Push(&q, pair{dist[v], v})
}
}
}
return ans
}
ans := make([]int64, n)
for i := range ans {
ans[i] = dijkstra(i)
}
return ans
}
type pair struct{ first, second int }
var _ heap.Interface = (*pairs)(nil)
type pairs []pair
func (a pairs) Len() int { return len(a) }
func (a pairs) Less(i int, j int) bool {
return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second
}
func (a pairs) Swap(i int, j int) { a[i], a[j] = a[j], a[i] }
func (a *pairs) Push(x any) { *a = append(*a, x.(pair)) }
func (a *pairs) Pop() any { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }