Skip to content

Latest commit

 

History

History
268 lines (237 loc) · 9.44 KB

README.md

File metadata and controls

268 lines (237 loc) · 9.44 KB
Raw

2247. K 条高速公路的最大旅行费用

English Version

题目描述

一系列高速公路连接从 0 到 n - 1 的 n 个城市。给定一个二维整数数组 highways，其中 highways[i] = [city1i, city2i, tolli] 表示有一条高速公路连接 city1i 和city2i，允许一辆汽车从 city1i 前往 city2i，反之亦然，费用为 tolli。

给你一个整数 k，你要正好经过 k 条公路。你可以从任何一个城市出发，但在旅途中每个城市最多只能访问一次。

返回您旅行的最大费用。如果没有符合要求的行程，则返回 -1。

示例 1:

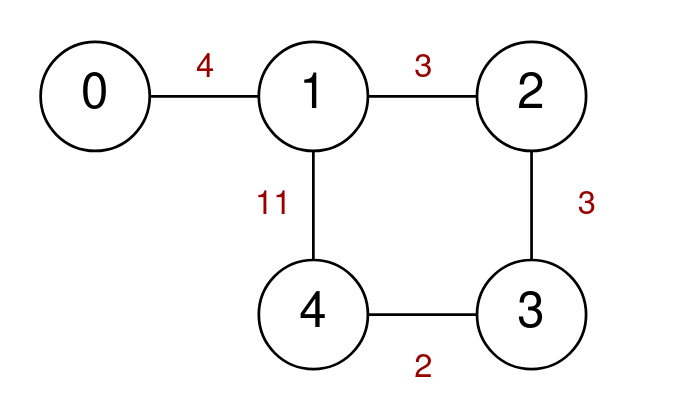
输入: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], k = 3
输出: 17
解释:
一个可能的路径是从 0 -> 1 -> 4 -> 3。这次旅行的费用是 4 + 11 + 2 = 17。
另一种可能的路径是从 4 -> 1 -> 2 -> 3。这次旅行的费用是 11 + 3 + 3 = 17。
可以证明，17 是任何有效行程的最大可能费用。
注意，旅行 4 -> 1 -> 0 -> 1 是不允许的，因为你访问了城市 1 两次。

 

示例 2:

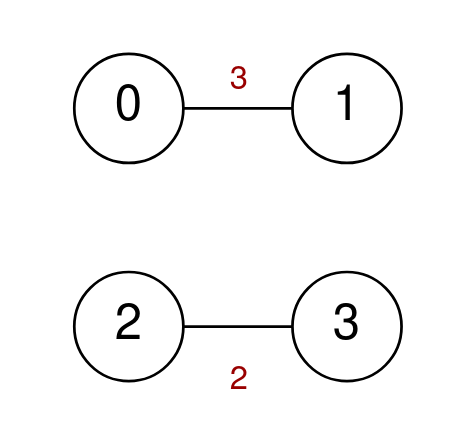
输入: n = 4, highways = [[0,1,3],[2,3,2]], k = 2
输出: -1
解释: 没有长度为 2 的有效行程，因此返回-1。

 

提示:

  • 2 <= n <= 15
  • 1 <= highways.length <= 50
  • highways[i].length == 3
  • 0 <= city1i, city2i <= n - 1
  • city1i != city2i
  • 0 <= tolli <= 100
  • 1 <= k <= 50

  • 没有重复的高速公路。

解法

方法一：状态压缩动态规划

我们注意到，题目要求正好经过 $k$ 条公路，而每个城市最多只能访问一次，城市的数量为 $n$，因此，我们最多只能经过 $n - 1$ 条公路。所以，如果 $k \ge n$，那么我们无法满足题目要求，直接返回 $-1$ 即可。

另外，我们也可以发现，城市数量 $n$ 不超过 $15$，这提示我们可以考虑使用状态压缩动态规划的方法求解本题。我们用一个长度为 $n$ 的二进制数表示当前已经经过的城市，其中第 $i$ 位为 $1$ 表示已经经过了第 $i$ 个城市，为 $0$ 表示还没有经过第 $i$ 个城市。

我们用 $f[i][j]$ 表示当前已经经过的城市为 $i$，最后一个经过的城市为 $j$ 的情况下，最大的旅行费用。初始时 $f[2^i][i]=0$，其余 $f[i][j]=-\infty$。

考虑 $f[i][j]$ 如何进行状态转移。对于 $f[i]$，我们枚举所有城市 $j$，如果 $i$ 的第 $j$ 位为 $1$，那么我们就可以从其它城市 $h$ 经过公路到达城市 $j$，此时 $f[i][j]$ 的值为 $f[i][h]+cost(h, j)$ 的最大值，其中 $cost(h, j)$ 表示从城市 $h$ 到城市 $j$ 的旅行费用。因此，我们可以得到状态转移方程：

$$ f[i][j]=\max_{h \in \text{city}}{f[i \backslash j][h]+cost(h, j)} $$

其中 $i \backslash j$ 表示将 $i$ 的第 $j$ 位变为 $0$。

求出 $f[i][j]$ 后，我们判断经过的城市数量是否为 $k+1$，即 $i$ 的二进制表示中 $1$ 的个数是否为 $k+1$，如果是，那么我们就更新答案为 $ans = \max(ans, f[i][j])$。

时间复杂度 $O(2^n \times n^2)$，空间复杂度 $O(2^n \times n)$。其中 $n$ 表示城市数量。

class Solution:
    def maximumCost(self, n: int, highways: List[List[int]], k: int) -> int:
        if k >= n:
            return -1
        g = defaultdict(list)
        for a, b, cost in highways:
            g[a].append((b, cost))
            g[b].append((a, cost))
        f = [[-inf] * n for _ in range(1 << n)]
        for i in range(n):
            f[1 << i][i] = 0
        ans = -1
        for i in range(1 << n):
            for j in range(n):
                if i >> j & 1:
                    for h, cost in g[j]:
                        if i >> h & 1:
                            f[i][j] = max(f[i][j], f[i ^ (1 << j)][h] + cost)
                if i.bit_count() == k + 1:
                    ans = max(ans, f[i][j])
        return ans
class Solution {
    public int maximumCost(int n, int[][] highways, int k) {
        if (k >= n) {
            return -1;
        }
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, h -> new ArrayList<>());
        for (int[] h : highways) {
            int a = h[0], b = h[1], cost = h[2];
            g[a].add(new int[] {b, cost});
            g[b].add(new int[] {a, cost});
        }
        int[][] f = new int[1 << n][n];
        for (int[] e : f) {
            Arrays.fill(e, -(1 << 30));
        }
        for (int i = 0; i < n; ++i) {
            f[1 << i][i] = 0;
        }
        int ans = -1;
        for (int i = 0; i < 1 << n; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i >> j & 1) == 1) {
                    for (var e : g[j]) {
                        int h = e[0], cost = e[1];
                        if ((i >> h & 1) == 1) {
                            f[i][j] = Math.max(f[i][j], f[i ^ (1 << j)][h] + cost);
                        }
                    }
                }
                if (Integer.bitCount(i) == k + 1) {
                    ans = Math.max(ans, f[i][j]);
                }
            }
        }
        return ans;
    }
}
class Solution {
public:
    int maximumCost(int n, vector<vector<int>>& highways, int k) {
        if (k >= n) {
            return -1;
        }
        vector<pair<int, int>> g[n];
        for (auto& h : highways) {
            int a = h[0], b = h[1], cost = h[2];
            g[a].emplace_back(b, cost);
            g[b].emplace_back(a, cost);
        }
        int f[1 << n][n];
        memset(f, -0x3f, sizeof(f));
        for (int i = 0; i < n; ++i) {
            f[1 << i][i] = 0;
        }
        int ans = -1;
        for (int i = 0; i < 1 << n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i >> j & 1) {
                    for (auto& [h, cost] : g[j]) {
                        if (i >> h & 1) {
                            f[i][j] = max(f[i][j], f[i ^ (1 << j)][h] + cost);
                        }
                    }
                }
                if (__builtin_popcount(i) == k + 1) {
                    ans = max(ans, f[i][j]);
                }
            }
        }
        return ans;
    }
};
func maximumCost(n int, highways [][]int, k int) int {
	if k >= n {
		return -1
	}
	g := make([][][2]int, n)
	for _, h := range highways {
		a, b, cost := h[0], h[1], h[2]
		g[a] = append(g[a], [2]int{b, cost})
		g[b] = append(g[b], [2]int{a, cost})
	}
	f := make([][]int, 1<<n)
	for i := range f {
		f[i] = make([]int, n)
		for j := range f[i] {
			f[i][j] = -(1 << 30)
		}
	}
	for i := 0; i < n; i++ {
		f[1<<i][i] = 0
	}
	ans := -1
	for i := 0; i < 1<<n; i++ {
		for j := 0; j < n; j++ {
			if i>>j&1 == 1 {
				for _, e := range g[j] {
					h, cost := e[0], e[1]
					if i>>h&1 == 1 {
						f[i][j] = max(f[i][j], f[i^(1<<j)][h]+cost)
					}
				}
			}
			if bits.OnesCount(uint(i)) == k+1 {
				ans = max(ans, f[i][j])
			}
		}
	}
	return ans
}
function maximumCost(n: number, highways: number[][], k: number): number {
    if (k >= n) {
        return -1;
    }
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [a, b, cost] of highways) {
        g[a].push([b, cost]);
        g[b].push([a, cost]);
    }
    const f: number[][] = Array(1 << n)
        .fill(0)
        .map(() => Array(n).fill(-(1 << 30)));
    for (let i = 0; i < n; ++i) {
        f[1 << i][i] = 0;
    }
    let ans = -1;
    for (let i = 0; i < 1 << n; ++i) {
        for (let j = 0; j < n; ++j) {
            if ((i >> j) & 1) {
                for (const [h, cost] of g[j]) {
                    if ((i >> h) & 1) {
                        f[i][j] = Math.max(f[i][j], f[i ^ (1 << j)][h] + cost);
                    }
                }
            }
            if (bitCount(i) === k + 1) {
                ans = Math.max(ans, f[i][j]);
            }
        }
    }
    return ans;
}

function bitCount(i: number): number {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}