You are given a 0-indexed m x n binary matrix grid.
In one operation, you can choose any i and j that meet the following conditions:
0 <= i < m0 <= j < ngrid[i][j] == 1
and change the values of all cells in row i and column j to zero.
Return the minimum number of operations needed to remove all 1's from grid.
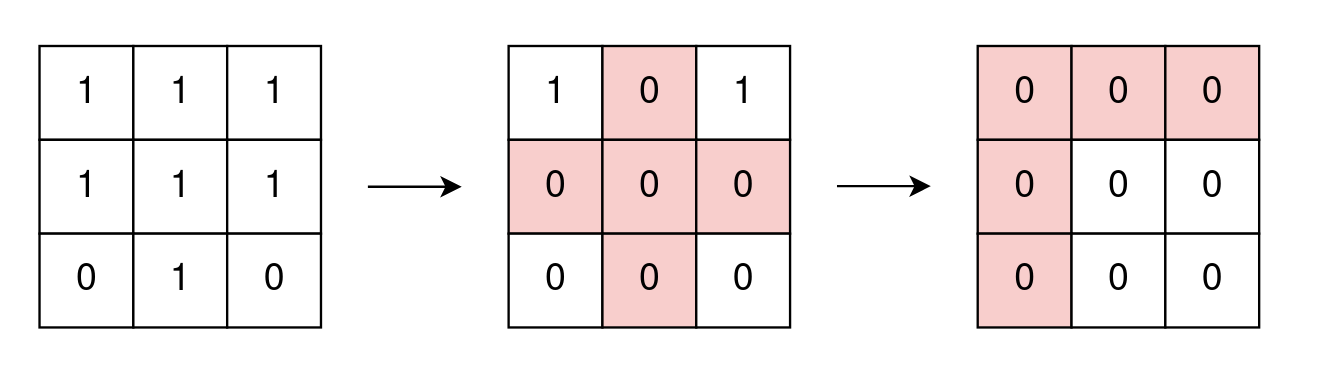
Example 1:
Input: grid = [[1,1,1],[1,1,1],[0,1,0]] Output: 2 Explanation: In the first operation, change all cell values of row 1 and column 1 to zero. In the second operation, change all cell values of row 0 and column 0 to zero.
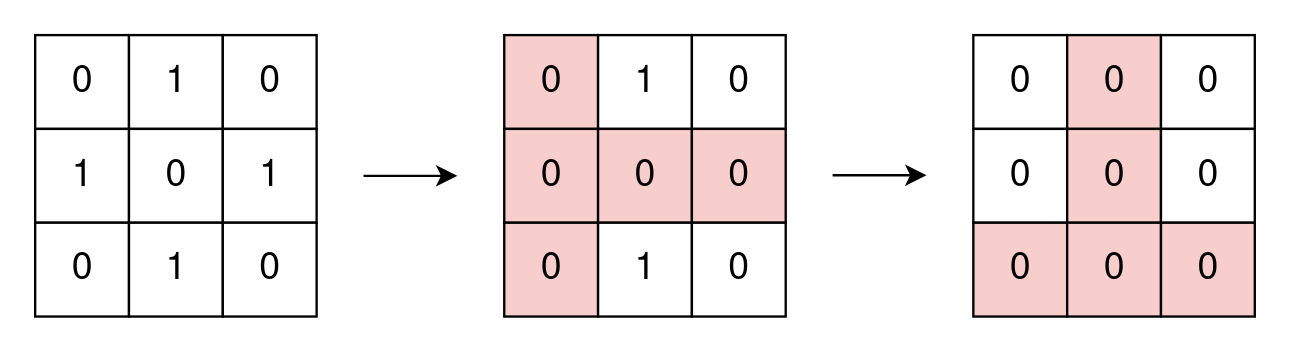
Example 2:
Input: grid = [[0,1,0],[1,0,1],[0,1,0]] Output: 2 Explanation: In the first operation, change all cell values of row 1 and column 0 to zero. In the second operation, change all cell values of row 2 and column 1 to zero. Note that we cannot perform an operation using row 1 and column 1 because grid[1][1] != 1.
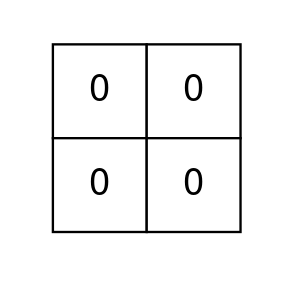
Example 3:
Input: grid = [[0,0],[0,0]] Output: 0 Explanation: There are no 1's to remove so return 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 151 <= m * n <= 15grid[i][j]is either0or1.
class Solution:
def removeOnes(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
state = sum(1 << (i * n + j) for i in range(m) for j in range(n) if grid[i][j])
q = deque([state])
vis = {state}
ans = 0
while q:
for _ in range(len(q)):
state = q.popleft()
if state == 0:
return ans
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
continue
nxt = state
for r in range(m):
nxt &= ~(1 << (r * n + j))
for c in range(n):
nxt &= ~(1 << (i * n + c))
if nxt not in vis:
vis.add(nxt)
q.append(nxt)
ans += 1
return -1class Solution {
public int removeOnes(int[][] grid) {
int m = grid.length, n = grid[0].length;
int state = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
state |= 1 << (i * n + j);
}
}
}
Deque<Integer> q = new ArrayDeque<>();
q.offer(state);
Set<Integer> vis = new HashSet<>();
vis.add(state);
int ans = 0;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
state = q.poll();
if (state == 0) {
return ans;
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
continue;
}
int nxt = state;
for (int r = 0; r < m; ++r) {
nxt &= ~(1 << (r * n + j));
}
for (int c = 0; c < n; ++c) {
nxt &= ~(1 << (i * n + c));
}
if (!vis.contains(nxt)) {
vis.add(nxt);
q.offer(nxt);
}
}
}
}
++ans;
}
return -1;
}
}class Solution {
public:
int removeOnes(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int state = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j])
state |= (1 << (i * n + j));
queue<int> q{{state}};
unordered_set<int> vis{{state}};
int ans = 0;
while (!q.empty()) {
for (int k = q.size(); k > 0; --k) {
state = q.front();
q.pop();
if (state == 0) return ans;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) continue;
int nxt = state;
for (int r = 0; r < m; ++r) nxt &= ~(1 << (r * n + j));
for (int c = 0; c < n; ++c) nxt &= ~(1 << (i * n + c));
if (!vis.count(nxt)) {
vis.insert(nxt);
q.push(nxt);
}
}
}
}
++ans;
}
return -1;
}
};func removeOnes(grid [][]int) int {
m, n := len(grid), len(grid[0])
state := 0
for i, row := range grid {
for j, v := range row {
if v == 1 {
state |= 1 << (i*n + j)
}
}
}
q := []int{state}
vis := map[int]bool{state: true}
ans := 0
for len(q) > 0 {
for k := len(q); k > 0; k-- {
state = q[0]
if state == 0 {
return ans
}
q = q[1:]
for i, row := range grid {
for j, v := range row {
if v == 0 {
continue
}
nxt := state
for r := 0; r < m; r++ {
nxt &= ^(1 << (r*n + j))
}
for c := 0; c < n; c++ {
nxt &= ^(1 << (i*n + c))
}
if !vis[nxt] {
vis[nxt] = true
q = append(q, nxt)
}
}
}
}
ans++
}
return -1
}