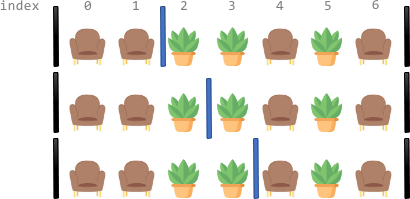
在一个图书馆的长廊里,有一些座位和装饰植物排成一列。给你一个下标从 0 开始,长度为 n 的字符串 corridor ,它包含字母 'S' 和 'P' ,其中每个 'S' 表示一个座位,每个 'P' 表示一株植物。
在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i 之间(1 <= i <= n - 1),至多能放一个屏风。
请你将走廊用屏风划分为若干段,且每一段内都 恰好有两个座位 ,而每一段内植物的数目没有要求。可能有多种划分方案,如果两个方案中有任何一个屏风的位置不同,那么它们被视为 不同 方案。
请你返回划分走廊的方案数。由于答案可能很大,请你返回它对 109 + 7 取余 的结果。如果没有任何方案,请返回 0 。
示例 1:
输入:corridor = "SSPPSPS" 输出:3 解释:总共有 3 种不同分隔走廊的方案。 上图中黑色的竖线表示已经放置好的屏风。 上图每种方案中,每一段都恰好有 两个 座位。
示例 2:
输入:corridor = "PPSPSP" 输出:1 解释:只有 1 种分隔走廊的方案,就是不放置任何屏风。 放置任何的屏风都会导致有一段无法恰好有 2 个座位。
示例 3:
输入:corridor = "S" 输出:0 解释:没有任何方案,因为总是有一段无法恰好有 2 个座位。
提示:
n == corridor.length1 <= n <= 105corridor[i]要么是'S',要么是'P'。
设计函数 dfs(i, cnt) 表示从下标 i 开始,且当前已经分配了 cnt 个座位的方案数。
对于下标 i 处的字符,如果是 S,那么 cnt 加 1,如果此时 cnt 超过 2,那么直接返回 0。
否则我们可以选择不放置屏风,此时的方案数为 dfs(i + 1, cnt);如果此时 cnt 为 2,我们还可以选择放置屏风,此时的方案数为 dfs(i + 1, 0)。
最终返回方案数,记忆化搜索即可。
时间复杂度 corridor 的长度。
class Solution:
def numberOfWays(self, corridor: str) -> int:
@cache
def dfs(i, cnt):
if i == n:
return int(cnt == 2)
cnt += corridor[i] == 'S'
if cnt > 2:
return 0
ans = dfs(i + 1, cnt)
if cnt == 2:
ans += dfs(i + 1, 0)
ans %= mod
return ans
n = len(corridor)
mod = 10**9 + 7
ans = dfs(0, 0)
dfs.cache_clear()
return ansclass Solution {
private String s;
private int n;
private int[][] f;
private static final int MOD = (int) 1e9 + 7;
public int numberOfWays(String corridor) {
s = corridor;
n = s.length();
f = new int[n][3];
for (var e : f) {
Arrays.fill(e, -1);
}
return dfs(0, 0);
}
private int dfs(int i, int cnt) {
if (i == n) {
return cnt == 2 ? 1 : 0;
}
cnt += s.charAt(i) == 'S' ? 1 : 0;
if (cnt > 2) {
return 0;
}
if (f[i][cnt] != -1) {
return f[i][cnt];
}
int ans = dfs(i + 1, cnt);
if (cnt == 2) {
ans += dfs(i + 1, 0);
ans %= MOD;
}
f[i][cnt] = ans;
return ans;
}
}class Solution {
public:
const int mod = 1e9 + 7;
int numberOfWays(string corridor) {
int n = corridor.size();
vector<vector<int>> f(n, vector<int>(3, -1));
function<int(int, int)> dfs;
dfs = [&](int i, int cnt) {
if (i == n) return cnt == 2 ? 1 : 0;
cnt += corridor[i] == 'S';
if (cnt > 2) return 0;
if (f[i][cnt] != -1) return f[i][cnt];
int ans = dfs(i + 1, cnt);
if (cnt == 2) {
ans += dfs(i + 1, 0);
ans %= mod;
}
f[i][cnt] = ans;
return ans;
};
return dfs(0, 0);
}
};func numberOfWays(corridor string) int {
n := len(corridor)
var mod int = 1e9 + 7
f := make([][]int, n)
for i := range f {
f[i] = make([]int, 3)
for j := range f[i] {
f[i][j] = -1
}
}
var dfs func(i, cnt int) int
dfs = func(i, cnt int) int {
if i == n {
if cnt == 2 {
return 1
}
return 0
}
if corridor[i] == 'S' {
cnt++
}
if cnt > 2 {
return 0
}
if f[i][cnt] != -1 {
return f[i][cnt]
}
ans := dfs(i+1, cnt)
if cnt == 2 {
ans += dfs(i+1, 0)
ans %= mod
}
f[i][cnt] = ans
return ans
}
return dfs(0, 0)
}function numberOfWays(corridor: string): number {
const M: number = 1e9 + 7;
const seatNumbers: number[] = [];
for (let i = 0; i < corridor.length; i++) {
if (corridor.charAt(i) === 'S') {
seatNumbers.push(i);
}
}
if (seatNumbers.length % 2 !== 0 || seatNumbers.length === 0) {
return 0;
}
let result: number = 1;
for (let i = 2; i < seatNumbers.length; i += 2) {
result = (result * (seatNumbers[i] - seatNumbers[i - 1])) % M;
}
return result;
}