一个 k x k 的 幻方 指的是一个 k x k 填满整数的方格阵,且每一行、每一列以及两条对角线的和 全部相等 。幻方中的整数 不需要互不相同 。显然,每个 1 x 1 的方格都是一个幻方。
给你一个 m x n 的整数矩阵 grid ,请你返回矩阵中 最大幻方 的 尺寸 (即边长 k)。
示例 1:
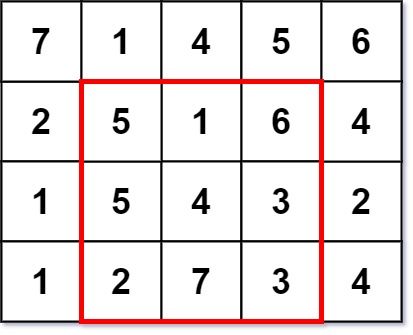
输入:grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]] 输出:3 解释:最大幻方尺寸为 3 。 每一行,每一列以及两条对角线的和都等于 12 。 - 每一行的和:5+1+6 = 5+4+3 = 2+7+3 = 12 - 每一列的和:5+5+2 = 1+4+7 = 6+3+3 = 12 - 对角线的和:5+4+3 = 6+4+2 = 12
示例 2:
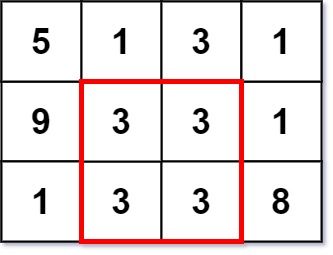
输入:grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]] 输出:2
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 106
class Solution:
def largestMagicSquare(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
rowsum = [[0] * (n + 1) for _ in range(m + 1)]
colsum = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1]
colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1]
def check(x1, y1, x2, y2):
val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1]
for i in range(x1 + 1, x2 + 1):
if rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val:
return False
for j in range(y1, y2 + 1):
if colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val:
return False
s, i, j = 0, x1, y1
while i <= x2:
s += grid[i][j]
i += 1
j += 1
if s != val:
return False
s, i, j = 0, x1, y2
while i <= x2:
s += grid[i][j]
i += 1
j -= 1
if s != val:
return False
return True
for k in range(min(m, n), 1, -1):
i = 0
while i + k - 1 < m:
j = 0
while j + k - 1 < n:
i2, j2 = i + k - 1, j + k - 1
if check(i, j, i2, j2):
return k
j += 1
i += 1
return 1class Solution {
private int[][] rowsum;
private int[][] colsum;
public int largestMagicSquare(int[][] grid) {
int m = grid.length, n = grid[0].length;
rowsum = new int[m + 1][n + 1];
colsum = new int[m + 1][n + 1];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1];
colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1];
}
}
for (int k = Math.min(m, n); k > 1; --k) {
for (int i = 0; i + k - 1 < m; ++i) {
for (int j = 0; j + k - 1 < n; ++j) {
int i2 = i + k - 1, j2 = j + k - 1;
if (check(grid, i, j, i2, j2)) {
return k;
}
}
}
}
return 1;
}
private boolean check(int[][] grid, int x1, int y1, int x2, int y2) {
int val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1];
for (int i = x1 + 1; i <= x2; ++i) {
if (rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val) {
return false;
}
}
for (int j = y1; j <= y2; ++j) {
if (colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val) {
return false;
}
}
int s = 0;
for (int i = x1, j = y1; i <= x2; ++i, ++j) {
s += grid[i][j];
}
if (s != val) {
return false;
}
s = 0;
for (int i = x1, j = y2; i <= x2; ++i, --j) {
s += grid[i][j];
}
if (s != val) {
return false;
}
return true;
}
}class Solution {
public:
int largestMagicSquare(vector<vector<int>>& grid) {
int m = grid.size(), n = grid.size();
vector<vector<int>> rowsum(m + 1, vector<int>(n + 1));
vector<vector<int>> colsum(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1];
colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1];
}
}
for (int k = min(m, n); k > 1; --k) {
for (int i = 0; i + k - 1 < m; ++i) {
for (int j = 0; j + k - 1 < n; ++j) {
int i2 = i + k - 1, j2 = j + k - 1;
if (check(grid, rowsum, colsum, i, j, i2, j2))
return k;
}
}
}
return 1;
}
bool check(vector<vector<int>>& grid, vector<vector<int>>& rowsum, vector<vector<int>>& colsum, int x1, int y1, int x2, int y2) {
int val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1];
for (int i = x1 + 1; i <= x2; ++i)
if (rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val)
return false;
for (int j = y1; j <= y2; ++j)
if (colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val)
return false;
int s = 0;
for (int i = x1, j = y1; i <= x2; ++i, ++j)
s += grid[i][j];
if (s != val)
return false;
s = 0;
for (int i = x1, j = y2; i <= x2; ++i, --j)
s += grid[i][j];
if (s != val)
return false;
return true;
}
};func largestMagicSquare(grid [][]int) int {
m, n := len(grid), len(grid[0])
rowsum := make([][]int, m+1)
colsum := make([][]int, m+1)
for i := 0; i <= m; i++ {
rowsum[i] = make([]int, n+1)
colsum[i] = make([]int, n+1)
}
for i := 1; i < m+1; i++ {
for j := 1; j < n+1; j++ {
rowsum[i][j] = rowsum[i][j-1] + grid[i-1][j-1]
colsum[i][j] = colsum[i-1][j] + grid[i-1][j-1]
}
}
for k := min(m, n); k > 1; k-- {
for i := 0; i+k-1 < m; i++ {
for j := 0; j+k-1 < n; j++ {
i2, j2 := i+k-1, j+k-1
if check(grid, rowsum, colsum, i, j, i2, j2) {
return k
}
}
}
}
return 1
}
func check(grid, rowsum, colsum [][]int, x1, y1, x2, y2 int) bool {
val := rowsum[x1+1][y2+1] - rowsum[x1+1][y1]
for i := x1 + 1; i < x2+1; i++ {
if rowsum[i+1][y2+1]-rowsum[i+1][y1] != val {
return false
}
}
for j := y1; j < y2+1; j++ {
if colsum[x2+1][j+1]-colsum[x1][j+1] != val {
return false
}
}
s := 0
for i, j := x1, y1; i <= x2; i, j = i+1, j+1 {
s += grid[i][j]
}
if s != val {
return false
}
s = 0
for i, j := x1, y2; i <= x2; i, j = i+1, j-1 {
s += grid[i][j]
}
if s != val {
return false
}
return true
}function largestMagicSquare(grid: number[][]): number {
let m = grid.length,
n = grid[0].length;
// 前缀和
let rowSum = Array.from({ length: m + 1 }, (v, i) => new Array(n + 1).fill(0)),
colSum = Array.from({ length: m + 1 }, v => new Array(n + 1).fill(0));
for (let i = 0; i < m; i++) {
rowSum[i + 1][1] = grid[i][0];
for (let j = 1; j < n; j++) {
rowSum[i + 1][j + 1] = rowSum[i + 1][j] + grid[i][j];
}
}
for (let j = 0; j < n; j++) {
colSum[1][j + 1] = grid[0][j];
for (let i = 1; i < m; i++) {
colSum[i + 1][j + 1] = colSum[i][j + 1] + grid[i][j];
}
}
// console.log(rowSum, colSum)
// 寻找最大k
for (let k = Math.min(m, n); k > 1; k--) {
for (let i = 0; i + k - 1 < m; i++) {
for (let j = 0; j + k - 1 < n; j++) {
let x2 = i + k - 1,
y2 = j + k - 1;
if (valid(grid, rowSum, colSum, i, j, x2, y2)) {
return k;
}
}
}
}
return 1;
}
function valid(
grid: number[][],
rowSum: number[][],
colSum: number[][],
x1: number,
y1: number,
x2: number,
y2: number,
): boolean {
let diff = rowSum[x1 + 1][y2 + 1] - rowSum[x1 + 1][y1];
// 行
for (let i = x1 + 1; i <= x2; i++) {
if (diff != rowSum[i + 1][y2 + 1] - rowSum[i + 1][y1]) {
return false;
}
}
// 列
for (let j = y1; j <= y2; j++) {
if (diff != colSum[x2 + 1][j + 1] - colSum[x1][j + 1]) {
return false;
}
}
// 主队对角线
let mainSum = diff;
for (let i = x1, j = y1; i <= x2; i++, j++) {
mainSum -= grid[i][j];
}
if (mainSum != 0) return false;
// 副对角线
let subSum = diff;
for (let i = x1, j = y2; i <= x2; i++, j--) {
subSum -= grid[i][j];
}
if (subSum != 0) return false;
return true;
}