README_EN.md

1824. Minimum Sideway Jumps

中文文档

Description

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

• For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

• For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

 

Example 1:

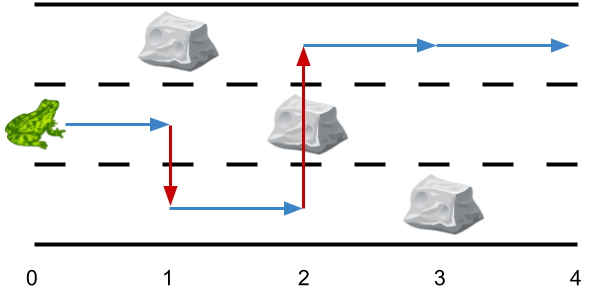
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2:

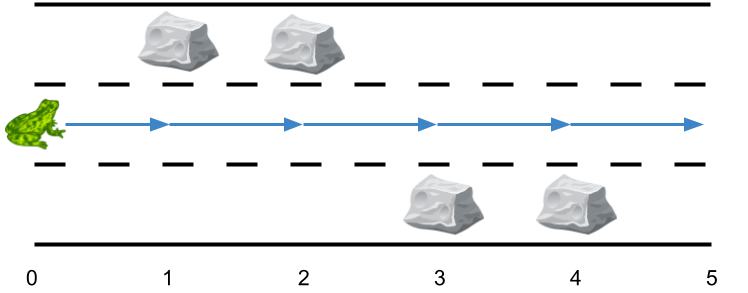
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3:

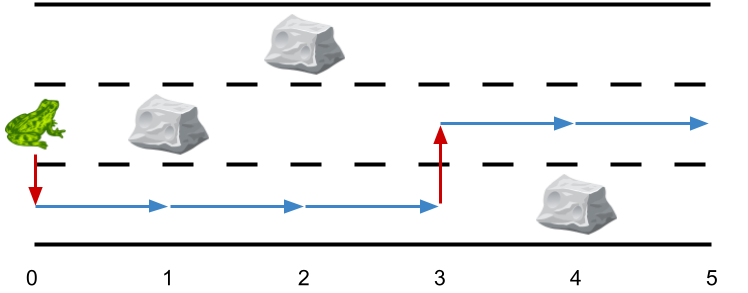
Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

 

Constraints:

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

Solutions

Solution 1: Dynamic Programming

We define $f[i][j]$ as the minimum number of sidesteps for the frog to reach the $i$-th point and be on the $j$-th lane (index starts from $0$).

Note that the frog starts on the second lane (the problem index starts from $1$), so the value of $f[0][1]$ is $0$, and the values of $f[0][0]$ and $f[0][2]$ are both $1$. The answer is $min(f[n][0], f[n][1], f[n][2])$.

For each position $i$ from $1$ to $n$, we can enumerate the current lane $j$ of the frog. If $obstacles[i] = j + 1$, it means that there is an obstacle on the $j$-th lane, and the value of $f[i][j]$ is infinity. Otherwise, the frog can choose not to jump, in which case the value of $f[i][j]$ is $f[i - 1][j]$, or the frog can sidestep from other lanes, in which case $f[i][j] = min(f[i][j], min(f[i][0], f[i][1], f[i][2]) + 1)$.

In the code implementation, we can optimize the first dimension of space and only use an array $f$ of length $3$ for maintenance.

The time complexity is $O(n)$, where $n$ is the length of the array $obstacles$. The space complexity is $O(1)$.

class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        f = [1, 0, 1]
        for v in obstacles[1:]:
            for j in range(3):
                if v == j + 1:
                    f[j] = inf
                    break
            x = min(f) + 1
            for j in range(3):
                if v != j + 1:
                    f[j] = min(f[j], x)
        return min(f)

class Solution {
    public int minSideJumps(int[] obstacles) {
        final int inf = 1 << 30;
        int[] f = {1, 0, 1};
        for (int i = 1; i < obstacles.length; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = Math.min(f[0], Math.min(f[1], f[2])) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = Math.min(f[j], x);
                }
            }
        }
        return Math.min(f[0], Math.min(f[1], f[2]));
    }
}

class Solution {
public:
    int minSideJumps(vector<int>& obstacles) {
        const int inf = 1 << 30;
        int f[3] = {1, 0, 1};
        for (int i = 1; i < obstacles.size(); ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = min({f[0], f[1], f[2]}) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = min(f[j], x);
                }
            }
        }
        return min({f[0], f[1], f[2]});
    }
};

func minSideJumps(obstacles []int) int {
	f := [3]int{1, 0, 1}
	const inf = 1 << 30
	for _, v := range obstacles[1:] {
		for j := 0; j < 3; j++ {
			if v == j+1 {
				f[j] = inf
				break
			}
		}
		x := min(f[0], min(f[1], f[2])) + 1
		for j := 0; j < 3; j++ {
			if v != j+1 {
				f[j] = min(f[j], x)
			}
		}
	}
	return min(f[0], min(f[1], f[2]))
}

function minSideJumps(obstacles: number[]): number {
    const inf = 1 << 30;
    const f = [1, 0, 1];
    for (let i = 1; i < obstacles.length; ++i) {
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] == j + 1) {
                f[j] = inf;
                break;
            }
        }
        const x = Math.min(...f) + 1;
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] != j + 1) {
                f[j] = Math.min(f[j], x);
            }
        }
    }
    return Math.min(...f);
}