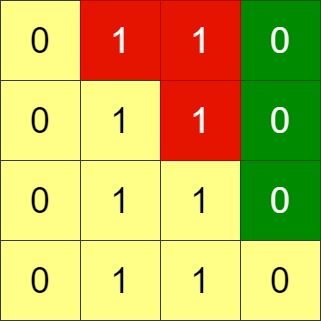
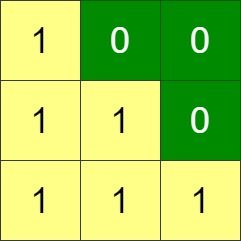
给你一个 n x n 的二进制网格 grid,每一次操作中,你可以选择网格的 相邻两行 进行交换。
一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。
请你返回使网格满足要求的最少操作次数,如果无法使网格符合要求,请你返回 -1 。
主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。
示例 1:
输入:grid = [[0,0,1],[1,1,0],[1,0,0]] 输出:3
示例 2:
输入:grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]] 输出:-1 解释:所有行都是一样的,交换相邻行无法使网格符合要求。
示例 3:
输入:grid = [[1,0,0],[1,1,0],[1,1,1]] 输出:0
提示:
n == grid.lengthn == grid[i].length1 <= n <= 200grid[i][j]要么是0要么是1。
我们逐行处理,对于第
时间复杂度
class Solution:
def minSwaps(self, grid: List[List[int]]) -> int:
n = len(grid)
pos = [-1] * n
for i in range(n):
for j in range(n - 1, -1, -1):
if grid[i][j] == 1:
pos[i] = j
break
ans = 0
for i in range(n):
k = -1
for j in range(i, n):
if pos[j] <= i:
ans += j - i
k = j
break
if k == -1:
return -1
while k > i:
pos[k], pos[k - 1] = pos[k - 1], pos[k]
k -= 1
return ansclass Solution {
public int minSwaps(int[][] grid) {
int n = grid.length;
int[] pos = new int[n];
Arrays.fill(pos, -1);
for (int i = 0; i < n; ++i) {
for (int j = n - 1; j >= 0; --j) {
if (grid[i][j] == 1) {
pos[i] = j;
break;
}
}
}
int ans = 0;
for (int i = 0; i < n; ++i) {
int k = -1;
for (int j = i; j < n; ++j) {
if (pos[j] <= i) {
ans += j - i;
k = j;
break;
}
}
if (k == -1) {
return -1;
}
for (; k > i; --k) {
int t = pos[k];
pos[k] = pos[k - 1];
pos[k - 1] = t;
}
}
return ans;
}
}class Solution {
public:
int minSwaps(vector<vector<int>>& grid) {
int n = grid.size();
vector<int> pos(n, -1);
for (int i = 0; i < n; ++i) {
for (int j = n - 1; j >= 0; --j) {
if (grid[i][j] == 1) {
pos[i] = j;
break;
}
}
}
int ans = 0;
for (int i = 0; i < n; ++i) {
int k = -1;
for (int j = i; j < n; ++j) {
if (pos[j] <= i) {
ans += j - i;
k = j;
break;
}
}
if (k == -1) {
return -1;
}
for (; k > i; --k) {
swap(pos[k], pos[k - 1]);
}
}
return ans;
}
};func minSwaps(grid [][]int) (ans int) {
n := len(grid)
pos := make([]int, n)
for i := range pos {
pos[i] = -1
}
for i := 0; i < n; i++ {
for j := n - 1; j >= 0; j-- {
if grid[i][j] == 1 {
pos[i] = j
break
}
}
}
for i := 0; i < n; i++ {
k := -1
for j := i; j < n; j++ {
if pos[j] <= i {
ans += j - i
k = j
break
}
}
if k == -1 {
return -1
}
for ; k > i; k-- {
pos[k], pos[k-1] = pos[k-1], pos[k]
}
}
return
}function minSwaps(grid: number[][]): number {
const n = grid.length;
const pos: number[] = Array(n).fill(-1);
for (let i = 0; i < n; ++i) {
for (let j = n - 1; ~j; --j) {
if (grid[i][j] === 1) {
pos[i] = j;
break;
}
}
}
let ans = 0;
for (let i = 0; i < n; ++i) {
let k = -1;
for (let j = i; j < n; ++j) {
if (pos[j] <= i) {
ans += j - i;
k = j;
break;
}
}
if (k === -1) {
return -1;
}
for (; k > i; --k) {
[pos[k], pos[k - 1]] = [pos[k - 1], pos[k]];
}
}
return ans;
}