(这是一个交互题)
我们称只包含元素 0 或 1 的矩阵为二进制矩阵。矩阵中每个单独的行都按非递减顺序排序。
给定一个这样的二进制矩阵,返回至少包含一个 1 的最左端列的索引(从 0 开始)。如果这样的列不存在,返回 -1。
您不能直接访问该二进制矩阵。你只可以通过 BinaryMatrix 接口来访问。
BinaryMatrix.get(row, col)返回位于索引(row, col)(从 0 开始)的元素。BinaryMatrix.dimensions()返回含有 2 个元素的列表[rows, cols],表示这是一个rows * cols的矩阵。
如果提交的答案调用 BinaryMatrix.get 超过 1000 次,则该答案会被判定为错误答案。提交任何试图规避判定机制的答案将会被取消资格。
下列示例中, mat 为给定的二进制矩阵。您不能直接访问该矩阵。
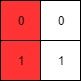
示例 1:
输入: mat = [[0,0],[1,1]] 输出: 0
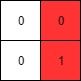
示例 2:
输入: mat = [[0,0],[0,1]] 输出: 1
示例 3:
输入: mat = [[0,0],[0,0]] 输出: -1
示例 4:
输入: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]] 输出: 1
提示:
rows == mat.lengthcols == mat[i].length1 <= rows, cols <= 100mat[i][j]只会是0或1。mat[i]已按非递减顺序排序。
我们先调用 BinaryMatrix.dimensions() 得到矩阵的行数
时间复杂度
# """
# This is BinaryMatrix's API interface.
# You should not implement it, or speculate about its implementation
# """
# class BinaryMatrix(object):
# def get(self, row: int, col: int) -> int:
# def dimensions(self) -> list[]:
class Solution:
def leftMostColumnWithOne(self, binaryMatrix: "BinaryMatrix") -> int:
m, n = binaryMatrix.dimensions()
ans = n
for i in range(m):
j = bisect_left(range(n), 1, key=lambda k: binaryMatrix.get(i, k))
ans = min(ans, j)
return -1 if ans >= n else ans/**
* // This is the BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* interface BinaryMatrix {
* public int get(int row, int col) {}
* public List<Integer> dimensions {}
* };
*/
class Solution {
public int leftMostColumnWithOne(BinaryMatrix binaryMatrix) {
List<Integer> e = binaryMatrix.dimensions();
int m = e.get(0), n = e.get(1);
int ans = n;
for (int i = 0; i < m; ++i) {
int l = 0, r = n;
while (l < r) {
int mid = (l + r) >> 1;
if (binaryMatrix.get(i, mid) == 1) {
r = mid;
} else {
l = mid + 1;
}
}
ans = Math.min(ans, l);
}
return ans >= n ? -1 : ans;
}
}/**
* // This is the BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* class BinaryMatrix {
* public:
* int get(int row, int col);
* vector<int> dimensions();
* };
*/
class Solution {
public:
int leftMostColumnWithOne(BinaryMatrix& binaryMatrix) {
auto e = binaryMatrix.dimensions();
int m = e[0], n = e[1];
int ans = n;
for (int i = 0; i < m; ++i) {
int l = 0, r = n;
while (l < r) {
int mid = (l + r) >> 1;
if (binaryMatrix.get(i, mid)) {
r = mid;
} else {
l = mid + 1;
}
}
ans = min(ans, l);
}
return ans >= n ? -1 : ans;
}
};/**
* // This is the BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* type BinaryMatrix struct {
* Get func(int, int) int
* Dimensions func() []int
* }
*/
func leftMostColumnWithOne(binaryMatrix BinaryMatrix) int {
e := binaryMatrix.Dimensions()
m, n := e[0], e[1]
ans := n
for i := 0; i < m; i++ {
l, r := 0, n
for l < r {
mid := (l + r) >> 1
if binaryMatrix.Get(i, mid) == 1 {
r = mid
} else {
l = mid + 1
}
}
ans = min(ans, l)
}
if ans >= n {
return -1
}
return ans
}/**
* // This is the BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* class BinaryMatrix {
* get(row: number, col: number): number {}
*
* dimensions(): number[] {}
* }
*/
function leftMostColumnWithOne(binaryMatrix: BinaryMatrix) {
const [m, n] = binaryMatrix.dimensions();
let ans = n;
for (let i = 0; i < m; ++i) {
let [l, r] = [0, n];
while (l < r) {
const mid = (l + r) >> 1;
if (binaryMatrix.get(i, mid) === 1) {
r = mid;
} else {
l = mid + 1;
}
}
ans = Math.min(ans, l);
}
return ans >= n ? -1 : ans;
}/**
* // This is the BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* struct BinaryMatrix;
* impl BinaryMatrix {
* fn get(row: i32, col: i32) -> i32;
* fn dimensions() -> Vec<i32>;
* };
*/
impl Solution {
pub fn left_most_column_with_one(binaryMatrix: &BinaryMatrix) -> i32 {
let e = binaryMatrix.dimensions();
let m = e[0] as usize;
let n = e[1] as usize;
let mut ans = n;
for i in 0..m {
let (mut l, mut r) = (0, n);
while l < r {
let mid = (l + r) / 2;
if binaryMatrix.get(i as i32, mid as i32) == 1 {
r = mid;
} else {
l = mid + 1;
}
}
ans = ans.min(l);
}
if ans >= n {
-1
} else {
ans as i32
}
}
}/**
* // This is BinaryMatrix's API interface.
* // You should not implement it, or speculate about its implementation
* class BinaryMatrix {
* public int Get(int row, int col) {}
* public IList<int> Dimensions() {}
* }
*/
class Solution {
public int LeftMostColumnWithOne(BinaryMatrix binaryMatrix) {
var e = binaryMatrix.Dimensions();
int m = e[0], n = e[1];
int ans = n;
for (int i = 0; i < m; ++i) {
int l = 0, r = n;
while (l < r) {
int mid = (l + r) >> 1;
if (binaryMatrix.Get(i, mid) == 1) {
r = mid;
} else {
l = mid + 1;
}
}
ans = Math.Min(ans, l);
}
return ans >= n ? -1 : ans;
}
}