你还记得那条风靡全球的贪吃蛇吗?
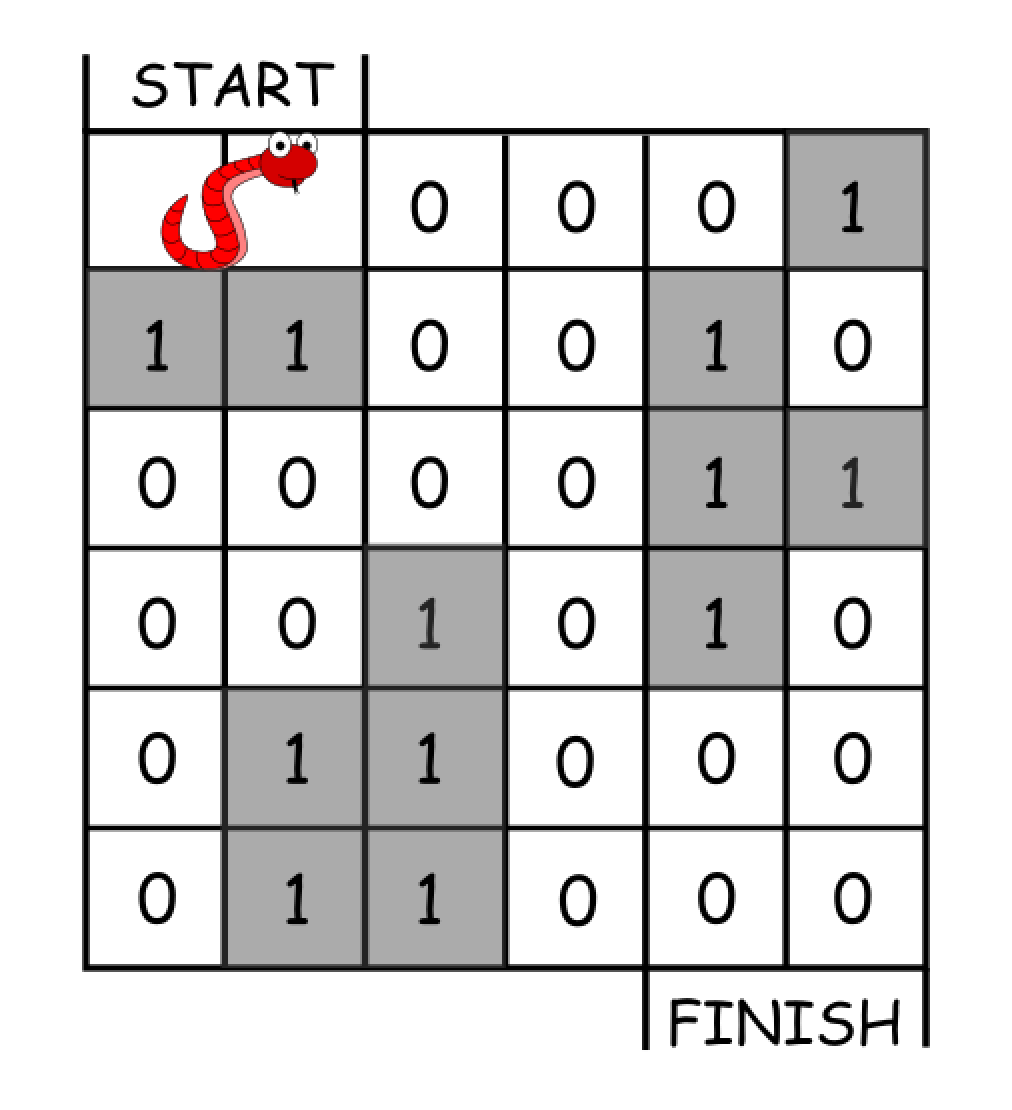
我们在一个 n*n 的网格上构建了新的迷宫地图,蛇的长度为 2,也就是说它会占去两个单元格。蛇会从左上角((0, 0) 和 (0, 1))开始移动。我们用 0 表示空单元格,用 1 表示障碍物。蛇需要移动到迷宫的右下角((n-1, n-2) 和 (n-1, n-1))。
每次移动,蛇可以这样走:
- 如果没有障碍,则向右移动一个单元格。并仍然保持身体的水平/竖直状态。
- 如果没有障碍,则向下移动一个单元格。并仍然保持身体的水平/竖直状态。
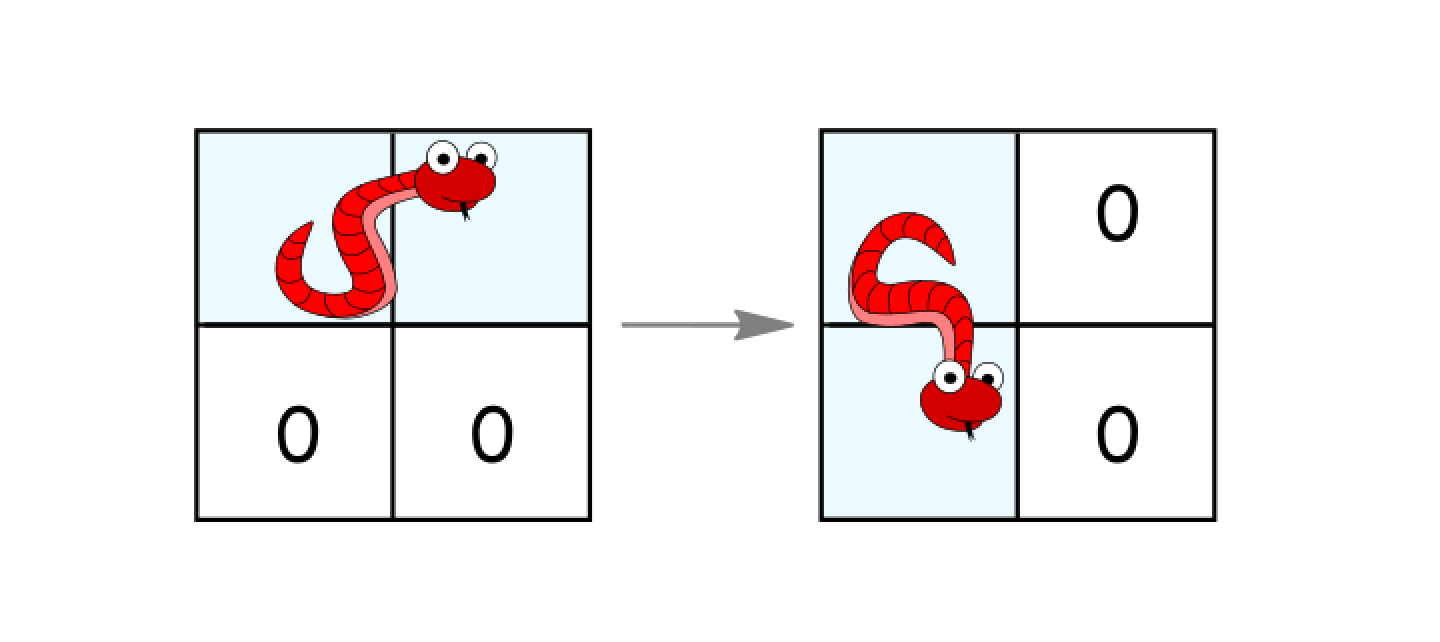
- 如果它处于水平状态并且其下面的两个单元都是空的,就顺时针旋转 90 度。蛇从(
(r, c)、(r, c+1))移动到 ((r, c)、(r+1, c))。
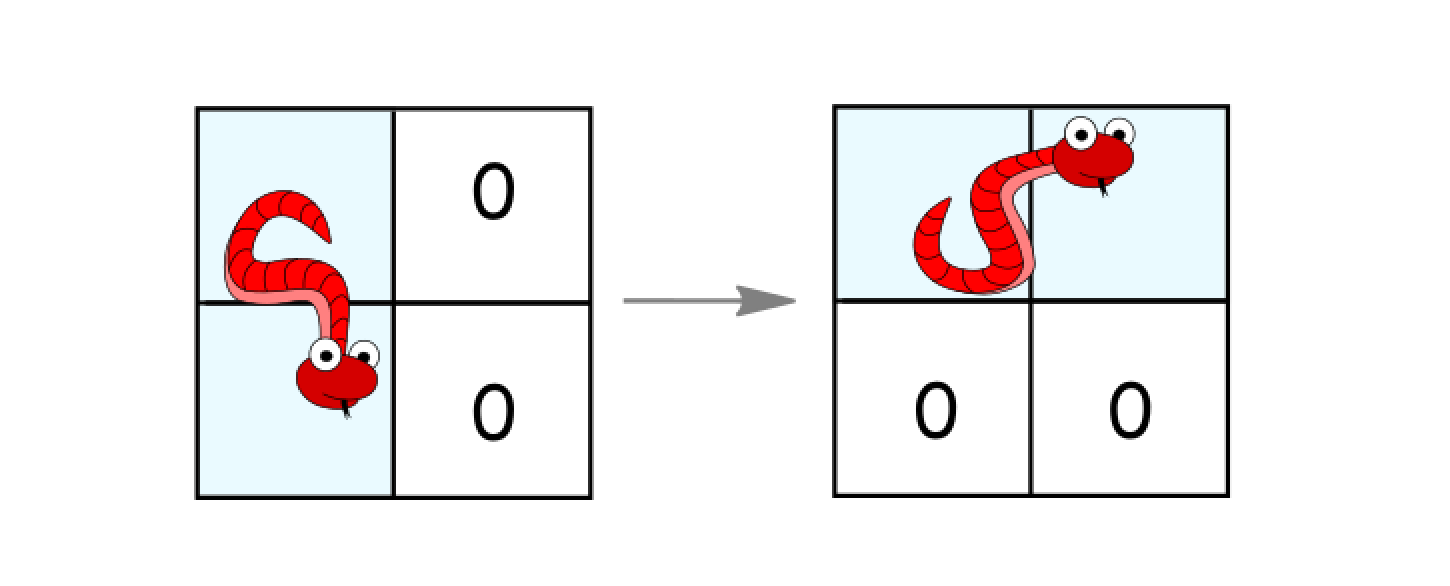
- 如果它处于竖直状态并且其右面的两个单元都是空的,就逆时针旋转 90 度。蛇从(
(r, c)、(r+1, c))移动到((r, c)、(r, c+1))。
返回蛇抵达目的地所需的最少移动次数。
如果无法到达目的地,请返回 -1。
示例 1:
输入:grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
输出:11
解释:
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。
示例 2:
输入:grid = [[0,0,1,1,1,1], [0,0,0,0,1,1], [1,1,0,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,0]] 输出:9
提示:
2 <= n <= 1000 <= grid[i][j] <= 1- 蛇保证从空单元格开始出发。
题目求的是蛇从起始位置到达目标位置的最少移动次数,我们考虑使用广度优先搜索
我们定义以下数据结构或变量:
- 队列
$q$ :存储蛇的当前位置,每个位置是一个二元组$(a, b)$ ,其中$a$ 表示蛇的尾部位置,而$b$ 表示蛇的头部位置。初始时,我们将位置$(0, 1)$ 加入队列$q$ 中。如果我们将二维迷宫扁平化成一个一维数组,那么位置$(0, 1)$ 就表示一维数组下标为$0$ 和$1$ 的两个单元格。 - 目标位置
$target$ :值固定为$(n^2 - 2, n^2 - 1)$ ,即二维迷宫的最后一行的最后两个单元格。 - 数组或集合
$vis$ :存储蛇的当前位置状态是否已经被访问过,每个状态是一个二元组$(a, status)$ ,其中$a$ 表示蛇的尾部位置;而$status$ 表示蛇当前所处的状态,取值为$0$ 或$1$ ,分别表示蛇的水平状态和垂直状态。初始时将起始位置$(0, 1)$ 的状态加入集合$vis$ 中。 - 答案变量
$ans$ :存储蛇从起始位置到达目标位置的移动次数,初始时为$0$ 。
我们使用广度优先搜索来求解,每次从队列
最后,如果队列
时间复杂度
class Solution:
def minimumMoves(self, grid: List[List[int]]) -> int:
def move(i1, j1, i2, j2):
if 0 <= i1 < n and 0 <= j1 < n and 0 <= i2 < n and 0 <= j2 < n:
a, b = i1 * n + j1, i2 * n + j2
status = 0 if i1 == i2 else 1
if (a, status) not in vis and grid[i1][j1] == 0 and grid[i2][j2] == 0:
q.append((a, b))
vis.add((a, status))
n = len(grid)
target = (n * n - 2, n * n - 1)
q = deque([(0, 1)])
vis = {(0, 0)}
ans = 0
while q:
for _ in range(len(q)):
a, b = q.popleft()
if (a, b) == target:
return ans
i1, j1 = a // n, a % n
i2, j2 = b // n, b % n
# 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1)
# 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2)
# 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if i1 == i2 and i1 + 1 < n and grid[i1 + 1][j2] == 0:
move(i1, j1, i1 + 1, j1)
# 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if j1 == j2 and j1 + 1 < n and grid[i2][j1 + 1] == 0:
move(i1, j1, i1, j1 + 1)
ans += 1
return -1class Solution {
private int n;
private int[][] grid;
private boolean[][] vis;
private Deque<int[]> q = new ArrayDeque<>();
public int minimumMoves(int[][] grid) {
this.grid = grid;
n = grid.length;
vis = new boolean[n * n][2];
int[] target = {n * n - 2, n * n - 1};
q.offer(new int[] {0, 1});
vis[0][0] = true;
int ans = 0;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
var p = q.poll();
if (p[0] == target[0] && p[1] == target[1]) {
return ans;
}
int i1 = p[0] / n, j1 = p[0] % n;
int i2 = p[1] / n, j2 = p[1] % n;
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}
private void move(int i1, int j1, int i2, int j2) {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
int a = i1 * n + j1, b = i2 * n + j2;
int status = i1 == i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.offer(new int[] {a, b});
vis[a][status] = true;
}
}
}
}class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int n = grid.size();
auto target = make_pair(n * n - 2, n * n - 1);
queue<pair<int, int>> q;
q.emplace(0, 1);
bool vis[n * n][2];
memset(vis, 0, sizeof vis);
vis[0][0] = true;
auto move = [&](int i1, int j1, int i2, int j2) {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
int a = i1 * n + j1, b = i2 * n + j2;
int status = i1 == i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.emplace(a, b);
vis[a][status] = true;
}
}
};
int ans = 0;
while (!q.empty()) {
for (int k = q.size(); k; --k) {
auto p = q.front();
q.pop();
if (p == target) {
return ans;
}
auto [a, b] = p;
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}
};func minimumMoves(grid [][]int) int {
n := len(grid)
type pair struct{ a, b int }
target := pair{n*n - 2, n*n - 1}
q := []pair{pair{0, 1}}
vis := make([][2]bool, n*n)
vis[0][0] = true
move := func(i1, j1, i2, j2 int) {
if i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n {
a, b := i1*n+j1, i2*n+j2
status := 1
if i1 == i2 {
status = 0
}
if !vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0 {
q = append(q, pair{a, b})
vis[a][status] = true
}
}
}
ans := 0
for len(q) > 0 {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
if p == target {
return ans
}
a, b := p.a, p.b
i1, j1 := a/n, a%n
i2, j2 := b/n, b%n
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1+1, i2, j2+1)
// 尝试向下平移(保持身体水平/垂直状态)
move(i1+1, j1, i2+1, j2)
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if i1 == i2 && i1+1 < n && grid[i1+1][j2] == 0 {
move(i1, j1, i1+1, j1)
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if j1 == j2 && j1+1 < n && grid[i2][j1+1] == 0 {
move(i1, j1, i1, j1+1)
}
}
ans++
}
return -1
}function minimumMoves(grid: number[][]): number {
const n = grid.length;
const target: number[] = [n * n - 2, n * n - 1];
const q: number[][] = [[0, 1]];
const vis = Array.from({ length: n * n }, () => Array(2).fill(false));
vis[0][0] = true;
const move = (i1: number, j1: number, i2: number, j2: number) => {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
const a = i1 * n + j1;
const b = i2 * n + j2;
const status = i1 === i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.push([a, b]);
vis[a][status] = true;
}
}
};
let ans = 0;
while (q.length) {
for (let k = q.length; k; --k) {
const p: number[] = q.shift();
if (p[0] === target[0] && p[1] === target[1]) {
return ans;
}
const [i1, j1] = [~~(p[0] / n), p[0] % n];
const [i2, j2] = [~~(p[1] / n), p[1] % n];
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
}/**
* @param {number[][]} grid
* @return {number}
*/
var minimumMoves = function (grid) {
const n = grid.length;
const target = [n * n - 2, n * n - 1];
const q = [[0, 1]];
const vis = Array.from({ length: n * n }, () => Array(2).fill(false));
vis[0][0] = true;
const move = (i1, j1, i2, j2) => {
if (i1 >= 0 && i1 < n && j1 >= 0 && j1 < n && i2 >= 0 && i2 < n && j2 >= 0 && j2 < n) {
const a = i1 * n + j1;
const b = i2 * n + j2;
const status = i1 === i2 ? 0 : 1;
if (!vis[a][status] && grid[i1][j1] == 0 && grid[i2][j2] == 0) {
q.push([a, b]);
vis[a][status] = true;
}
}
};
let ans = 0;
while (q.length) {
for (let k = q.length; k; --k) {
const p = q.shift();
if (p[0] === target[0] && p[1] === target[1]) {
return ans;
}
const [i1, j1] = [~~(p[0] / n), p[0] % n];
const [i2, j2] = [~~(p[1] / n), p[1] % n];
// 尝试向右平移(保持身体水平/垂直状态)
move(i1, j1 + 1, i2, j2 + 1);
// 尝试向下平移(保持身体水平/垂直状态)
move(i1 + 1, j1, i2 + 1, j2);
// 当前处于水平状态,且 grid[i1 + 1][j2] 无障碍,尝试顺时针旋转90°
if (i1 == i2 && i1 + 1 < n && grid[i1 + 1][j2] == 0) {
move(i1, j1, i1 + 1, j1);
}
// 当前处于垂直状态,且 grid[i2][j1 + 1] 无障碍,尝试逆时针旋转90°
if (j1 == j2 && j1 + 1 < n && grid[i2][j1 + 1] == 0) {
move(i1, j1, i1, j1 + 1);
}
}
++ans;
}
return -1;
};