有 n 个项目,每个项目或者不属于任何小组,或者属于 m 个小组之一。group[i] 表示第 i 个项目所属的小组,如果第 i 个项目不属于任何小组,则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目,即没有任何项目属于这个小组。
请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表:
- 同一小组的项目,排序后在列表中彼此相邻。
- 项目之间存在一定的依赖关系,我们用一个列表
beforeItems来表示,其中beforeItems[i]表示在进行第i个项目前(位于第i个项目左侧)应该完成的所有项目。
如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。
示例 1:
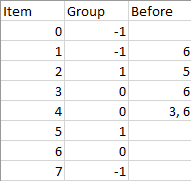
输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]] 输出:[6,3,4,1,5,2,0,7]
示例 2:
输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]] 输出:[] 解释:与示例 1 大致相同,但是在排序后的列表中,4 必须放在 6 的前面。
提示:
1 <= m <= n <= 3 * 104group.length == beforeItems.length == n-1 <= group[i] <= m - 10 <= beforeItems[i].length <= n - 10 <= beforeItems[i][j] <= n - 1i != beforeItems[i][j]beforeItems[i]不含重复元素
我们先遍历数组
接下来,我们需要建图。对于每个项目,我们需要建立两种图,一种是项目间的图,一种是小组间的图。我们遍历数组
接下来,我们先对小组间的图进行拓扑排序,得到排序后的小组列表
时间复杂度
class Solution:
def sortItems(
self, n: int, m: int, group: List[int], beforeItems: List[List[int]]
) -> List[int]:
def topo_sort(degree, graph, items):
q = deque(i for _, i in enumerate(items) if degree[i] == 0)
res = []
while q:
i = q.popleft()
res.append(i)
for j in graph[i]:
degree[j] -= 1
if degree[j] == 0:
q.append(j)
return res if len(res) == len(items) else []
idx = m
group_items = [[] for _ in range(n + m)]
for i, g in enumerate(group):
if g == -1:
group[i] = idx
idx += 1
group_items[group[i]].append(i)
item_degree = [0] * n
group_degree = [0] * (n + m)
item_graph = [[] for _ in range(n)]
group_graph = [[] for _ in range(n + m)]
for i, gi in enumerate(group):
for j in beforeItems[i]:
gj = group[j]
if gi == gj:
item_degree[i] += 1
item_graph[j].append(i)
else:
group_degree[gi] += 1
group_graph[gj].append(gi)
group_order = topo_sort(group_degree, group_graph, range(n + m))
if not group_order:
return []
ans = []
for gi in group_order:
items = group_items[gi]
item_order = topo_sort(item_degree, item_graph, items)
if len(items) != len(item_order):
return []
ans.extend(item_order)
return ansclass Solution {
public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
int idx = m;
List<Integer>[] groupItems = new List[n + m];
int[] itemDegree = new int[n];
int[] groupDegree = new int[n + m];
List<Integer>[] itemGraph = new List[n];
List<Integer>[] groupGraph = new List[n + m];
Arrays.setAll(groupItems, k -> new ArrayList<>());
Arrays.setAll(itemGraph, k -> new ArrayList<>());
Arrays.setAll(groupGraph, k -> new ArrayList<>());
for (int i = 0; i < n; ++i) {
if (group[i] == -1) {
group[i] = idx++;
}
groupItems[group[i]].add(i);
}
for (int i = 0; i < n; ++i) {
for (int j : beforeItems.get(i)) {
if (group[i] == group[j]) {
++itemDegree[i];
itemGraph[j].add(i);
} else {
++groupDegree[group[i]];
groupGraph[group[j]].add(group[i]);
}
}
}
List<Integer> items = new ArrayList<>();
for (int i = 0; i < n + m; ++i) {
items.add(i);
}
var groupOrder = topoSort(groupDegree, groupGraph, items);
if (groupOrder.isEmpty()) {
return new int[0];
}
List<Integer> ans = new ArrayList<>();
for (int gi : groupOrder) {
items = groupItems[gi];
var itemOrder = topoSort(itemDegree, itemGraph, items);
if (itemOrder.size() != items.size()) {
return new int[0];
}
ans.addAll(itemOrder);
}
return ans.stream().mapToInt(Integer::intValue).toArray();
}
private List<Integer> topoSort(int[] degree, List<Integer>[] graph, List<Integer> items) {
Deque<Integer> q = new ArrayDeque<>();
for (int i : items) {
if (degree[i] == 0) {
q.offer(i);
}
}
List<Integer> ans = new ArrayList<>();
while (!q.isEmpty()) {
int i = q.poll();
ans.add(i);
for (int j : graph[i]) {
if (--degree[j] == 0) {
q.offer(j);
}
}
}
return ans.size() == items.size() ? ans : List.of();
}
}class Solution {
public:
vector<int> sortItems(int n, int m, vector<int>& group, vector<vector<int>>& beforeItems) {
int idx = m;
vector<vector<int>> groupItems(n + m);
vector<int> itemDegree(n);
vector<int> groupDegree(n + m);
vector<vector<int>> itemGraph(n);
vector<vector<int>> groupGraph(n + m);
for (int i = 0; i < n; ++i) {
if (group[i] == -1) {
group[i] = idx++;
}
groupItems[group[i]].push_back(i);
}
for (int i = 0; i < n; ++i) {
for (int j : beforeItems[i]) {
if (group[i] == group[j]) {
++itemDegree[i];
itemGraph[j].push_back(i);
} else {
++groupDegree[group[i]];
groupGraph[group[j]].push_back(group[i]);
}
}
}
vector<int> items(n + m);
iota(items.begin(), items.end(), 0);
auto topoSort = [](vector<vector<int>>& graph, vector<int>& degree, vector<int>& items) -> vector<int> {
queue<int> q;
for (int& i : items) {
if (degree[i] == 0) {
q.push(i);
}
}
vector<int> ans;
while (!q.empty()) {
int i = q.front();
q.pop();
ans.push_back(i);
for (int& j : graph[i]) {
if (--degree[j] == 0) {
q.push(j);
}
}
}
return ans.size() == items.size() ? ans : vector<int>();
};
auto groupOrder = topoSort(groupGraph, groupDegree, items);
if (groupOrder.empty()) {
return vector<int>();
}
vector<int> ans;
for (int& gi : groupOrder) {
items = groupItems[gi];
auto itemOrder = topoSort(itemGraph, itemDegree, items);
if (items.size() != itemOrder.size()) {
return vector<int>();
}
ans.insert(ans.end(), itemOrder.begin(), itemOrder.end());
}
return ans;
}
};func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
idx := m
groupItems := make([][]int, n+m)
itemDegree := make([]int, n)
groupDegree := make([]int, n+m)
itemGraph := make([][]int, n)
groupGraph := make([][]int, n+m)
for i, g := range group {
if g == -1 {
group[i] = idx
idx++
}
groupItems[group[i]] = append(groupItems[group[i]], i)
}
for i, gi := range group {
for _, j := range beforeItems[i] {
gj := group[j]
if gi == gj {
itemDegree[i]++
itemGraph[j] = append(itemGraph[j], i)
} else {
groupDegree[gi]++
groupGraph[gj] = append(groupGraph[gj], gi)
}
}
}
items := make([]int, n+m)
for i := range items {
items[i] = i
}
topoSort := func(degree []int, graph [][]int, items []int) []int {
q := []int{}
for _, i := range items {
if degree[i] == 0 {
q = append(q, i)
}
}
ans := []int{}
for len(q) > 0 {
i := q[0]
q = q[1:]
ans = append(ans, i)
for _, j := range graph[i] {
degree[j]--
if degree[j] == 0 {
q = append(q, j)
}
}
}
return ans
}
groupOrder := topoSort(groupDegree, groupGraph, items)
if len(groupOrder) != len(items) {
return nil
}
ans := []int{}
for _, gi := range groupOrder {
items = groupItems[gi]
itemOrder := topoSort(itemDegree, itemGraph, items)
if len(items) != len(itemOrder) {
return nil
}
ans = append(ans, itemOrder...)
}
return ans
}function sortItems(n: number, m: number, group: number[], beforeItems: number[][]): number[] {
let idx = m;
const groupItems: number[][] = new Array(n + m).fill(0).map(() => []);
const itemDegree: number[] = new Array(n).fill(0);
const gorupDegree: number[] = new Array(n + m).fill(0);
const itemGraph: number[][] = new Array(n).fill(0).map(() => []);
const groupGraph: number[][] = new Array(n + m).fill(0).map(() => []);
for (let i = 0; i < n; ++i) {
if (group[i] === -1) {
group[i] = idx++;
}
groupItems[group[i]].push(i);
}
for (let i = 0; i < n; ++i) {
for (const j of beforeItems[i]) {
if (group[i] === group[j]) {
++itemDegree[i];
itemGraph[j].push(i);
} else {
++gorupDegree[group[i]];
groupGraph[group[j]].push(group[i]);
}
}
}
let items = new Array(n + m).fill(0).map((_, i) => i);
const topoSort = (graph: number[][], degree: number[], items: number[]): number[] => {
const q: number[] = [];
for (const i of items) {
if (degree[i] === 0) {
q.push(i);
}
}
const ans: number[] = [];
while (q.length) {
const i = q.pop()!;
ans.push(i);
for (const j of graph[i]) {
if (--degree[j] === 0) {
q.push(j);
}
}
}
return ans.length === items.length ? ans : [];
};
const groupOrder = topoSort(groupGraph, gorupDegree, items);
if (groupOrder.length === 0) {
return [];
}
const ans: number[] = [];
for (const gi of groupOrder) {
items = groupItems[gi];
const itemOrder = topoSort(itemGraph, itemDegree, items);
if (itemOrder.length !== items.length) {
return [];
}
ans.push(...itemOrder);
}
return ans;
}