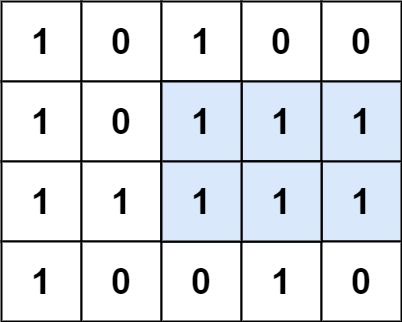
Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
Example 1:
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 6 Explanation: The maximal rectangle is shown in the above picture.
Example 2:
Input: matrix = [["0"]] Output: 0
Example 3:
Input: matrix = [["1"]] Output: 1
Constraints:
rows == matrix.lengthcols == matrix[i].length1 <= row, cols <= 200matrix[i][j]is'0'or'1'.
We treat each row as the base of the histogram, and calculate the maximum area of the histogram for each row.
The time complexity is
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
heights = [0] * len(matrix[0])
ans = 0
for row in matrix:
for j, v in enumerate(row):
if v == "1":
heights[j] += 1
else:
heights[j] = 0
ans = max(ans, self.largestRectangleArea(heights))
return ans
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
stk = []
left = [-1] * n
right = [n] * n
for i, h in enumerate(heights):
while stk and heights[stk[-1]] >= h:
stk.pop()
if stk:
left[i] = stk[-1]
stk.append(i)
stk = []
for i in range(n - 1, -1, -1):
h = heights[i]
while stk and heights[stk[-1]] >= h:
stk.pop()
if stk:
right[i] = stk[-1]
stk.append(i)
return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))class Solution {
public int maximalRectangle(char[][] matrix) {
int n = matrix[0].length;
int[] heights = new int[n];
int ans = 0;
for (var row : matrix) {
for (int j = 0; j < n; ++j) {
if (row[j] == '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
ans = Math.max(ans, largestRectangleArea(heights));
}
return ans;
}
private int largestRectangleArea(int[] heights) {
int res = 0, n = heights.length;
Deque<Integer> stk = new ArrayDeque<>();
int[] left = new int[n];
int[] right = new int[n];
Arrays.fill(right, n);
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
right[stk.pop()] = i;
}
left[i] = stk.isEmpty() ? -1 : stk.peek();
stk.push(i);
}
for (int i = 0; i < n; ++i) {
res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
}
return res;
}
}class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int n = matrix[0].size();
vector<int> heights(n);
int ans = 0;
for (auto& row : matrix) {
for (int j = 0; j < n; ++j) {
if (row[j] == '1')
++heights[j];
else
heights[j] = 0;
}
ans = max(ans, largestRectangleArea(heights));
}
return ans;
}
int largestRectangleArea(vector<int>& heights) {
int res = 0, n = heights.size();
stack<int> stk;
vector<int> left(n, -1);
vector<int> right(n, n);
for (int i = 0; i < n; ++i) {
while (!stk.empty() && heights[stk.top()] >= heights[i]) {
right[stk.top()] = i;
stk.pop();
}
if (!stk.empty()) left[i] = stk.top();
stk.push(i);
}
for (int i = 0; i < n; ++i)
res = max(res, heights[i] * (right[i] - left[i] - 1));
return res;
}
};func maximalRectangle(matrix [][]byte) int {
n := len(matrix[0])
heights := make([]int, n)
ans := 0
for _, row := range matrix {
for j, v := range row {
if v == '1' {
heights[j]++
} else {
heights[j] = 0
}
}
ans = max(ans, largestRectangleArea(heights))
}
return ans
}
func largestRectangleArea(heights []int) int {
res, n := 0, len(heights)
var stk []int
left, right := make([]int, n), make([]int, n)
for i := range right {
right[i] = n
}
for i, h := range heights {
for len(stk) > 0 && heights[stk[len(stk)-1]] >= h {
right[stk[len(stk)-1]] = i
stk = stk[:len(stk)-1]
}
if len(stk) > 0 {
left[i] = stk[len(stk)-1]
} else {
left[i] = -1
}
stk = append(stk, i)
}
for i, h := range heights {
res = max(res, h*(right[i]-left[i]-1))
}
return res
}impl Solution {
#[allow(dead_code)]
pub fn maximal_rectangle(matrix: Vec<Vec<char>>) -> i32 {
let n = matrix[0].len();
let mut heights = vec![0; n];
let mut ret = -1;
for row in &matrix {
Self::array_builder(row, &mut heights);
ret = std::cmp::max(ret, Self::largest_rectangle_area(heights.clone()));
}
ret
}
/// Helper function, build the heights array according to the input
#[allow(dead_code)]
fn array_builder(input: &Vec<char>, heights: &mut Vec<i32>) {
for (i, &c) in input.iter().enumerate() {
heights[i] += match c {
'1' => 1,
'0' => {
heights[i] = 0;
0
}
_ => panic!("This is impossible"),
};
}
}
/// Helper function, see: https://leetcode.com/problems/largest-rectangle-in-histogram/ for details
#[allow(dead_code)]
fn largest_rectangle_area(heights: Vec<i32>) -> i32 {
let n = heights.len();
let mut left = vec![-1; n];
let mut right = vec![-1; n];
let mut stack: Vec<(usize, i32)> = Vec::new();
let mut ret = -1;
// Build left vector
for (i, h) in heights.iter().enumerate() {
while !stack.is_empty() && stack.last().unwrap().1 >= *h {
stack.pop();
}
if stack.is_empty() {
left[i] = -1;
} else {
left[i] = stack.last().unwrap().0 as i32;
}
stack.push((i, *h));
}
stack.clear();
// Build right vector
for (i, h) in heights.iter().enumerate().rev() {
while !stack.is_empty() && stack.last().unwrap().1 >= *h {
stack.pop();
}
if stack.is_empty() {
right[i] = n as i32;
} else {
right[i] = stack.last().unwrap().0 as i32;
}
stack.push((i, *h));
}
// Calculate the max area
for (i, h) in heights.iter().enumerate() {
ret = std::cmp::max(ret, (right[i] - left[i] - 1) * *h);
}
ret
}
}using System;
using System.Collections.Generic;
using System.Linq;
public class Solution {
private int MaximalRectangleHistagram(int[] height) {
var stack = new Stack<int>();
var result = 0;
var i = 0;
while (i < height.Length || stack.Any())
{
if (!stack.Any() || (i < height.Length && height[stack.Peek()] < height[i]))
{
stack.Push(i);
++i;
}
else
{
var previousIndex = stack.Pop();
var area = height[previousIndex] * (stack.Any() ? (i - stack.Peek() - 1) : i);
result = Math.Max(result, area);
}
}
return result;
}
public int MaximalRectangle(char[][] matrix) {
var lenI = matrix.Length;
var lenJ = lenI == 0 ? 0 : matrix[0].Length;
var height = new int[lenJ];
var result = 0;
for (var i = 0; i < lenI; ++i)
{
for (var j = 0; j < lenJ; ++j)
{
if (matrix[i][j] == '1')
{
++height[j];
}
else
{
height[j] = 0;
}
}
result = Math.Max(result, MaximalRectangleHistagram(height));
}
return result;
}
}