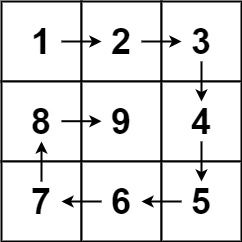
Given a positive integer n, generate an n x n matrix filled with elements from 1 to n2 in spiral order.
Example 1:
Input: n = 3 Output: [[1,2,3],[8,9,4],[7,6,5]]
Example 2:
Input: n = 1 Output: [[1]]
Constraints:
1 <= n <= 20
Directly simulate the generation process of the spiral matrix.
Define a two-dimensional array ans to store the spiral matrix. Use i and j to represent the row number and column number of the current position, use k to represent the current direction number, and dirs to represent the correspondence between the direction number and the direction.
Starting from 1, fill in each position of the matrix in turn. After filling in a position each time, calculate the row number and column number of the next position. If the next position is not in the matrix or has been filled, change the direction, and then calculate the row number and column number of the next position.
The time complexity is
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
ans = [[0] * n for _ in range(n)]
dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))
i = j = k = 0
for v in range(1, n * n + 1):
ans[i][j] = v
x, y = i + dirs[k][0], j + dirs[k][1]
if x < 0 or y < 0 or x >= n or y >= n or ans[x][y]:
k = (k + 1) % 4
x, y = i + dirs[k][0], j + dirs[k][1]
i, j = x, y
return ansclass Solution {
public int[][] generateMatrix(int n) {
int[][] ans = new int[n][n];
int i = 0, j = 0, k = 0;
int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
for (int v = 1; v <= n * n; ++v) {
ans[i][j] = v;
int x = i + dirs[k][0], y = j + dirs[k][1];
if (x < 0 || y < 0 || x >= n || y >= n || ans[x][y] > 0) {
k = (k + 1) % 4;
x = i + dirs[k][0];
y = j + dirs[k][1];
}
i = x;
j = y;
}
return ans;
}
}class Solution {
public:
const int dirs[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> ans(n, vector<int>(n));
int i = 0, j = 0, k = 0;
for (int v = 1; v <= n * n; ++v) {
ans[i][j] = v;
int x = i + dirs[k][0], y = j + dirs[k][1];
if (x < 0 || y < 0 || x >= n || y >= n || ans[x][y]) {
k = (k + 1) % 4;
x = i + dirs[k][0], y = j + dirs[k][1];
}
i = x, j = y;
}
return ans;
}
};func generateMatrix(n int) [][]int {
ans := make([][]int, n)
for i := range ans {
ans[i] = make([]int, n)
}
dirs := [4][2]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
var i, j, k int
for v := 1; v <= n*n; v++ {
ans[i][j] = v
x, y := i+dirs[k][0], j+dirs[k][1]
if x < 0 || y < 0 || x >= n || y >= n || ans[x][y] > 0 {
k = (k + 1) % 4
x, y = i+dirs[k][0], j+dirs[k][1]
}
i, j = x, y
}
return ans
}function generateMatrix(n: number): number[][] {
let ans = Array.from({ length: n }, v => new Array(n));
let dir = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0],
];
let i = 0,
j = 0;
for (let cnt = 1, k = 0; cnt <= n * n; cnt++) {
ans[i][j] = cnt;
let x = i + dir[k][0],
y = j + dir[k][1];
if (x < 0 || x == n || y < 0 || y == n || ans[x][y]) {
k = (k + 1) % 4;
(x = i + dir[k][0]), (y = j + dir[k][1]);
}
(i = x), (j = y);
}
return ans;
}impl Solution {
pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
let n = n as usize;
let mut res = vec![vec![0; n]; n];
let mut num = 1;
for i in 0..n / 2 {
for j in i..n - i - 1 {
res[i][j] = num;
num += 1;
}
for j in i..n - i - 1 {
res[j][n - i - 1] = num;
num += 1;
}
for j in i..n - i - 1 {
res[n - i - 1][n - j - 1] = num;
num += 1;
}
for j in i..n - i - 1 {
res[n - j - 1][i] = num;
num += 1;
}
}
if n % 2 == 1 {
res[n >> 1][n >> 1] = num;
}
res
}
}/**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function (n) {
const ans = new Array(n).fill(0).map(() => new Array(n).fill(0));
let [i, j, k] = [0, 0, 0];
const dirs = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0],
];
for (let v = 1; v <= n * n; ++v) {
ans[i][j] = v;
let [x, y] = [i + dirs[k][0], j + dirs[k][1]];
if (x < 0 || y < 0 || x >= n || y >= n || ans[x][y] > 0) {
k = (k + 1) % 4;
[x, y] = [i + dirs[k][0], j + dirs[k][1]];
}
[i, j] = [x, y];
}
return ans;
};function generateMatrix(n: number): number[][] {
const res = new Array(n).fill(0).map(() => new Array(n).fill(0));
let num = 1;
for (let i = 0; i < Math.floor(n / 2); i++) {
for (let j = i; j < n - i - 1; j++) {
res[i][j] = num++;
}
for (let j = i; j < n - i - 1; j++) {
res[j][n - i - 1] = num++;
}
for (let j = i; j < n - i - 1; j++) {
res[n - i - 1][n - j - 1] = num++;
}
for (let j = i; j < n - i - 1; j++) {
res[n - j - 1][i] = num++;
}
}
if (n % 2 === 1) {
res[n >> 1][n >> 1] = num;
}
return res;
}