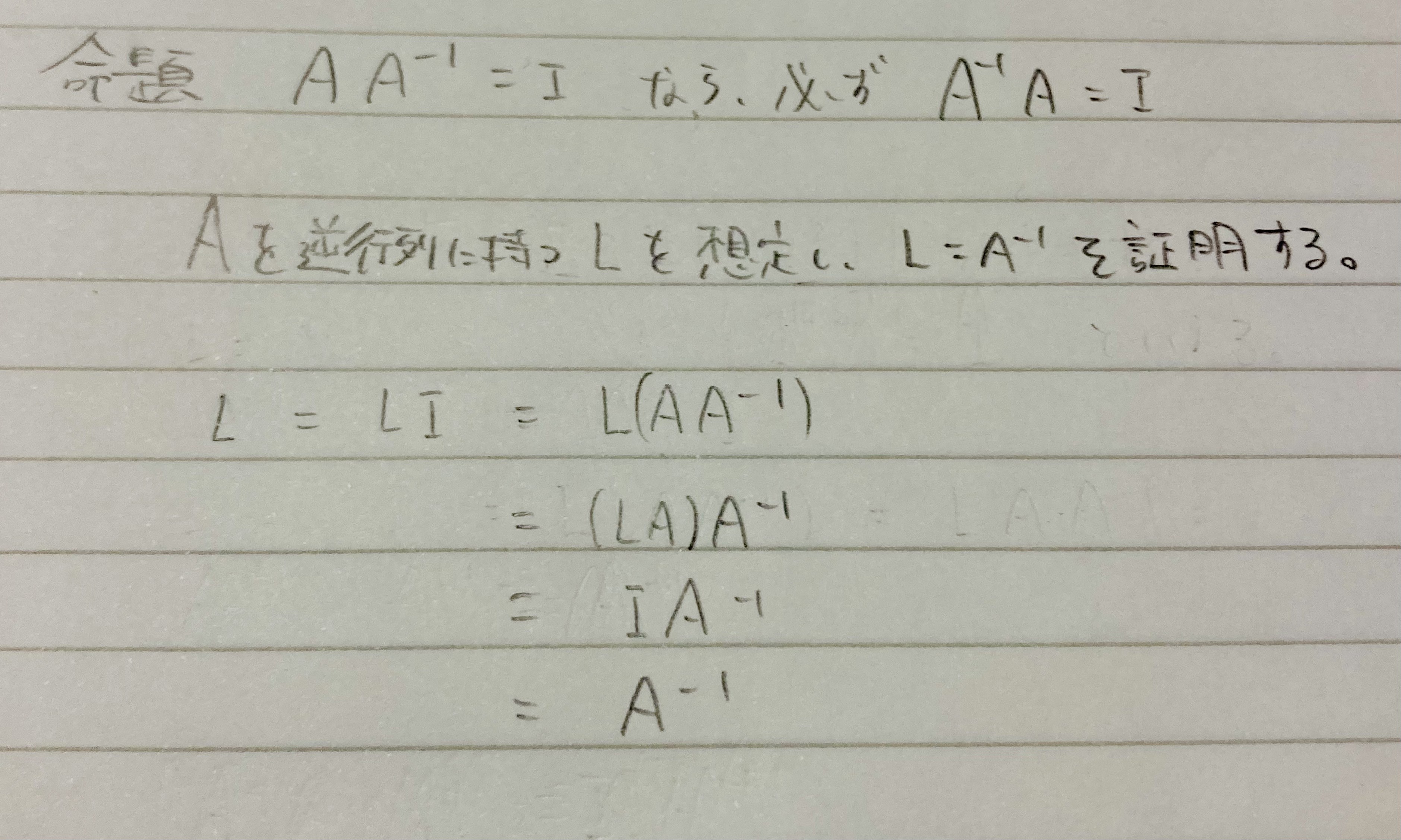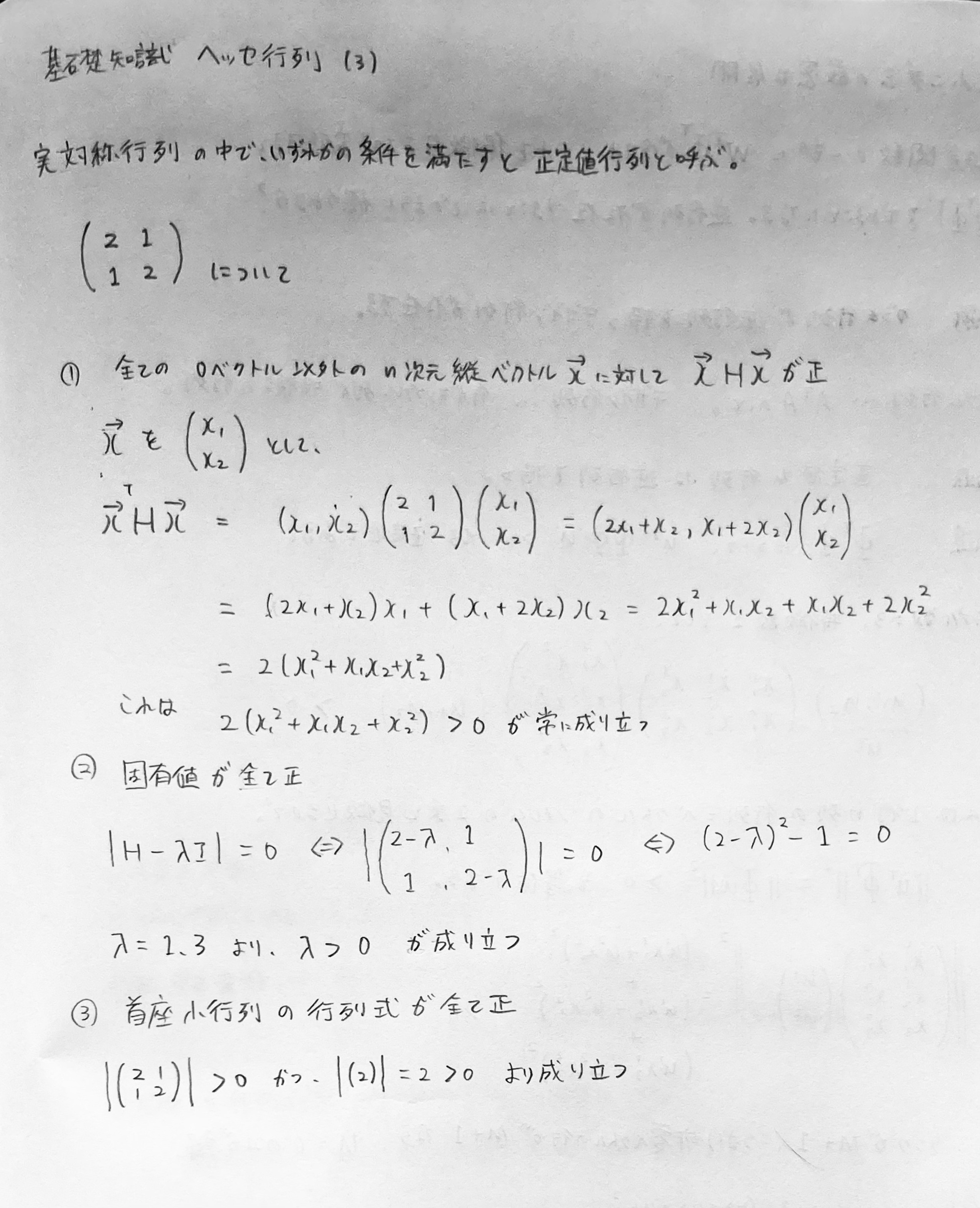README.md

代数学 (algebra)

ページ構成の際、次の情報源を参考にした。

• 実例で学ぶゲーム3D数学
• ゲーム開発のための数学・物理学入門 改訂版
• 線形代数キャンパス・ゼミ 改訂11

ベクトル (vector)

ベクトル。19世紀に様々な数学者が独自の定義を発表する中で、ポーランドの高校の数学教師だったグラスマンの理論が現在に続いている。¹

ベクトルの演算

ノルム (norm)

ベクトルの長さ。ピタゴラスの定理を用いて、各次元の2乗の和のルート2で求める。

内積 (dot product)

2つのベクトルの向きと大きさを反映する量を考える。ベクトルの向きが揃っているほど量が大きくなるようにしたい。直交座標系でベクトルを表す値として座標がある。座標において向きが揃うとは、大まかに言えばX軸,Y軸の各軸で正負の符号が揃っていることだから、2つのベクトルの各軸の成分の積和がちょうど良い量になりそうだ。前述の直感から納得できる、そのような量を内積(dot product, inner product)またはスカラー積(scalar product)という。

$$ \begin{align} a \cdot b = \sum_{i=1}^n a_i b_i \end{align} $$

内積は向きと大きさを反映した量だから、それらに分解することもできそうだ。向きは角度によって表せる。内積はベクトルの向きが揃っているほど大きく、直交すると0になり、逆を向くとマイナスになる。これは角というより余角に連動しているように見える。つまり、余弦が使えそうだ。²前述の直感から納得できる、極座標系における内積の定義は次の通り。

$$ \begin{align} a \cdot b = |a||b|\cos\theta \end{align} $$

ここまで、2つのベクトルの向きと大きさを反映した量を内積と呼んでいるが、改めて適切な名前を考えたい。内積を定義した、ポーランドの高校の数学教師であったグラスマンは、最初はベクトルを線形積と呼んでいた。（演算が）線形というのは、足し算や掛け算を演算の前後どちらでしても、計算結果が変わらないことをいう。内積についてどちらも言えるので、線形積という名前も良さそうだ。

グラスマンが内積という名前をつけたのは、内積が2つのベクトルに対する基本的な演算であること、外積との比較を受けてと思われる。グラスマンは次のように述べている。³

「内積の値は $\vec{a}$ と $\vec{b}$ が垂直ならば 0 で、その値が正になるためには、$\vec{b}$が少し $\vec{a}$ の『内側』の方に入らないといけないから、これを『内積』と呼ぶ。」

物理学的には、力と移動距離から仕事量を求める際に用いる。図（内積と仕事）では、50mの間200Nが水平方向に変換されただけの力を発揮した、ということになる。内積は交換法則が成り立つが、図の例で言えば200Mを50N（が水平方向に変換されただけ）の力も同じ仕事量、ということになる。

射影, 残差

ベクトルの作る影や、ベクトルどうしの垂直距離を考える。ベクトルの影は、2つのべクトルの角度が近いほど長く、垂直に近づくほど短くなる。つまり余角に連動している。ベクトルが他のベクトルになす影を射影といい、次の式で表す。

$$ \begin{align} proj_a b = |b| \cos\theta \frac{a}{|a|} = \frac{a \cdot b}{|a|^2}a \end{align} $$

Tip

2つのべクトル $c=(c_x, c_y)$ と $d=(d_x, d_y)$ が与えられている。$c$ が $d$ になす射影べクトルを求めよ。ただし、すでに $d$ に平行な単位ベクトル $e=(e_x, e_y)$ が分かっているので、それを用いること。

解答

射影のノルムが光の当たるベクトルのノルムと余弦の積である一方、内積は両方のべクトルのノルムと余弦の席である。したがって、影ができるべクトルのノルムが1なら、内積は射影のノルムに等しい。よって、内積と単位ベクトルの積が答えとなる。

次に、べクトルからベクトルへの垂直距離を考える。ベクトルから射影の成分を引いた残りの成分として表され、残差という。

コサイン類似度

ベクトルの内積をノルムの積で割ったもの。つまり、2つのベクトルのなす角Θに対するcosの値である。

Desmos(🔐)も参照。

外積

行列 (matrix)

行列の種類

次のような包含関係になっている。

行列 ⊇ 正方行列 ⊇ 対称行列 ⊇ 対角行列 ⊇ 単位行列 ⊇ 零行列

それぞれの性質は次の通り。行列を$A$とする。

• 行列
  • 転置（$A^T$）ができる
• 正方行列
  • 行列式（$|A|$）が定義できる
  • 正則行列であるとき、逆行列（$A^{-1}$）が存在する
  • ケーリー・ハミルトンの定理が成り立つ
  • 変換行列によって対角化できる
  • 乗算（$A^n$）が定義できる
• 対称行列 (symmetric matrix)
  • 転置した行列がもとの行列と等しい
• 対角行列 (diagonal matrix)
  • 対角要素以外が全て0である
• 非正方行列
  • 擬似逆行列（$A^+）が定義できる

正則行列, 逆行列 (regular matrix, inverse matrix)

$AA^{-1} = A^{-1}A = I$ が成り立つ時、$A$を正則行列または可逆行列、$A^{-1}$を逆行列と呼ぶ。

逆行列を考えるにあたって、まずは数学に登場する「逆」がつく概念を見直す。

• 逆数: $a$ の逆数は $1/a$。aを掛けた数にaの逆数を掛けると元の数に戻る。
• 逆関数: $f(x)$ の逆関数は $f^{-1}(x)$。関数の返り値を逆関数に渡すと、その返り値は元の値になる。

つまり、数学で「逆」がつく数・操作は、元の数に戻す性質があると言えそうだ。

[!NOTE] A^{-1}A = I なら、必ずAA^{-1} = I は成り立つ？ 次の通り成り立つ。

直交行列 (orthogonal matrix)

$R^TR = RR^T = I$ となる正方行列を、直交行列と呼ぶ。言い換えると、自身を転置した行列が逆行列の場合、直交行列である。

行列の演算

行列の積

行列の積は、次の図のように計算する。

1つ目の行の要素数と2つ目の列の要素数を一致させることに、身近な例から意味を見出したい。例えば、1つ目の行列を何世帯かの家族構成、2つ目の行列を行楽施設ごとの入場料とする。家族・行楽施設ごとの入場料金を計算する場合、家族構成が大人・子どもの人数なら、行楽施設ごとの入場料金も大人・子ども別の料金である必要がある。これはm行2列の行列と2行n列の行列の積として表せる。

行列のn乗

離散的な時刻単位の状態遷移を考える時、その変化を一般化して考えられると便利である。

例えば、2つの町の人口の変化を考える。町Aから町Bに毎年20%が引っ越し、逆に町Bから町Aに30%が引っ越すとする。このような、状態が直前の状態にだけ依存するものをマルコフ過程 (Markov process)という。1年後や2年後の計算は簡単である。定常状態、つまり無限年後についても、$人口 = 確率推移行列 \cdot 人口$のような方程式で解ける。しかし、100年後やn年後を計算するにはどうしたらいいか。

別の例として、隣接行列で表現された重み無し有向グラフを考える。頂点Aから頂点Bに1ステップで移動できるかは、A行B列の値が0か1かを見ればよい。ちょうど2ステップの場合は、隣接行列を2乗すればよい。しかしnステップの場合はどうか。

行列をn乗することで、n単位時間後の状態が分かる。行列のn乗を計算する方法は次の通り。⁴

1. 対角行列の場合、要素をそれぞれn乗する
2. 行列が対角化可能である場合、$P^{-1} A P$で挟んで対角化し、要素をそれぞれn乗した後、左辺と右辺にそれぞれ$P$と$P^{-1}$を掛けて相殺する
3. 行列が対角化できない場合、ケーリー・ハミルトンの定理 (C-H定理, Cayley–Hamilton theorem)を用いる

ケーリー・ハミルトンの定理は次の通り。

1. 固有多項式を展開した上で、ベクトル$x$ではなく行列を代入し、また右辺を零行列とする。この方程式をケーリー・ハミルトンの恒等式という。
2. 行列の累乗を固有多項式の積と、固有多項式の行列をスカラー値として解いた値を含む式の和として表し、その値から累乗を計算する

行列式

関数としての行列の可逆性をどのように知るのがよいか。例えば、ペイントソフトで図形を変形させた後、逆の操作で元に戻せるかが知りたいとする。これは、逆行列が存在するかを知りたい、と言い換えることができる。

別の例として、3つのベクトルから成る平行六面体の体積の計算を考える。立体では、2つ以上のベクトルが同じ直線上にあったり、3つのベクトルが同じ平面上にある場合は体積が0になる。言い換えると、3つのベクトルがお互いに他の2つのベクトルの線形結合では表せない場合に、非ゼロの体積を計算することができる。ここで、ベクトルの実数倍の和を線形結合といい、あるベクトルが他のベクトルの線形結合で表せる場合を線形従属、表せない場合を線形独立という。

関数の可逆性とベクトルの線形独立性は、どちらも行列の次元を保存できるかを問うている。つまり、行基本変形によってゼロベクトルの行または列が作られないことを確かめたい。ここで、n×n行列において、各行と各列から1つずつ要素を選び、それらの積を作る。このような積をn!通り作り、それらの符号付きの和を行列式と呼ぶ。行列式が0でない場合は、ゼロベクトルの行や列が無いことが言え、行列によって次元が落ちることがない。

3次以下の行列式の求め方として、サラスの公式がある。要素を列ごとに逆袈裟に総積した総和から、袈裟斬りに総積した総和を引いた値を行列式とする。ただし、左右端はトーラス状に繋がっていると考える。

行列$A$から、対角要素が全て同じ値の対角行列$\lambda I$を引いた行列を求めるその行列式が0となる方程式を固有方程式と呼び、$\lambda$の値を固有値という。

行列式などの概念を次の通り表にまとめた。

行列の線形変換

行列の基本変形, 簡約化, ランク

行列において、行の定数倍を任意の行に足す操作を基本変形と呼ぶ。（行の入れ替えは、行Aに-A+Bを、行Bに-B+Aを行う操作と見做せる）

また、基本変形によって簡約行列を作ることを簡約化と呼ぶ。簡約行列において、零ベクトル以外の行の数をランクと呼ぶ。

行列の対角化

固有値が全て正である行列を正定値行列と呼ぶ。次の条件を満たす行列を正定値行列と呼ぶ。条件は同値なので、実際には計算しやすい値を使って判定すればよい。

1. 任意の非零ベクトル $(x)$ に対して、$( x^T A x > 0 )$ が成り立つ。
2. 行列 $(A)$ の固有値が全て正である。
3. 行列 $(A)$ のすべての主要小行列の行列式が正である。

正定値行列であれば逆行列を持つ。また、多変数関数の二階偏導関数から導かれるヘッセ行列が正定値行列のとき、極値を持つ条件が分かる。

次の手順で正方行列から対角行列を作れる。

1. 固有多項式の右辺を0として固有方程式とし、それも解いて固有値を求める
2. 固有方程式に固有値を代入し、固有ベクトルを求める
3. 固有ベクトルを連結して変換行列$P$を求める
4. $P^{-1}AP$を計算し、対角行列になっていることを確かめる

対角行列のn乗は簡単に計算できるため、正方行列が行列の次元数と同じ数の固有ベクトルを持っていれば、対角行列を作ってからn乗を計算するのが良さそうだ。

なお、固有方程式で登場する$A - \lambda I$を特性行列 (characteristic matrix)という。

その他の参考文献

• 🔐数学B 改訂版 - 数研出版
• 線形代数キャンパス・ゼミ 改訂11
• 仕事と運動エネルギーとの関係 - 理数系学習サイト kori

Footnotes

1. 地球惑星数理演習 ベクトルとテンソル - 吉田茂生 ↩

2. 数学記号の由来について（7）－三角関数（sin、cos、tan等）－ の図解が分かりやすい。 ↩

3. 数学に関する質問とその背景の数学 - 竹野茂治 ↩

4. 行列のn乗計算 ↩