We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
对于一元 N 次方程,当 N 大于 2 时没有固定的求根公式,为了求方程的根,可以使用牛顿迭代法。
牛顿迭代法的思想是在曲线上任意取一个点,然后求这一点的切线,使用切线的解来逼近多项式的解。
然后在 处继续做切线:
不断的逼近,可以看到上图中切斜的解 已经接近真实的解 了一些。
这个过切点的直线的方程为:
令 可以求得 ,这里 与 的关系如下:
其中 表示 在 处的斜率。
求某个数(如 N)的平方根,可以理解为求如下函数的解:
其中 的导数为:
牛顿迭代式为:
利用以上原理可以写出下面代码:
def sqrt(n): if n < 0: return float('nan') # 因为牛顿迭代法只是逼近真实值,所以需要设置一个误差范围 e = 1e-15 x = n x_next = (x + n / x) / 2 # 两次迭代得到的解之间相差小于误差允许范围后跳出 while abs(x_next - x) > e: x = x_next # 计算下一个近似解 x_next = (x + n / x) / 2 return x
The text was updated successfully, but these errors were encountered:
No branches or pull requests
牛顿迭代法
对于一元 N 次方程,当 N 大于 2 时没有固定的求根公式,为了求方程的根,可以使用牛顿迭代法。
牛顿迭代法的思想是在曲线上任意取一个点,然后求这一点的切线,使用切线的解来逼近多项式的解。
然后在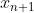 处继续做切线:
处继续做切线:
不断的逼近,可以看到上图中切斜的解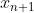 已经接近真实的解
已经接近真实的解 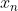 了一些。
了一些。
这个过切点的直线的方程为:
令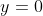 可以求得
可以求得 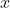 ,这里
,这里 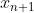 与
与 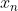 的关系如下:
的关系如下:
其中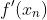 表示
表示 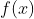 在
在 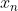 处的斜率。
处的斜率。
使用牛顿迭代法求平方根
求某个数(如 N)的平方根,可以理解为求如下函数的解:
其中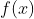 的导数为:
的导数为:
牛顿迭代式为:
利用以上原理可以写出下面代码:
The text was updated successfully, but these errors were encountered: