diff --git "a/content/posts/algorithm/trick/\346\232\264\345\212\233\351\200\222\345\275\222-\345\233\236\346\272\257.md" "b/content/posts/algorithm/trick/\346\232\264\345\212\233\351\200\222\345\275\222-\345\233\236\346\272\257.md" index 0e23c9d..6127ec7 100644 --- "a/content/posts/algorithm/trick/\346\232\264\345\212\233\351\200\222\345\275\222-\345\233\236\346\272\257.md" +++ "b/content/posts/algorithm/trick/\346\232\264\345\212\233\351\200\222\345\275\222-\345\233\236\346\272\257.md" @@ -1,14 +1,69 @@ --- -title: '暴力递归-回溯' +title: '暴力递归-dfs&回溯' date: 2022-10-09T20:49:13+08:00 -lastmod: 2024-03-07 +lastmod: 2024-03-27 series: [trick] categories: [algorithm] --- -## 排列组合(permutation and combination) +## 概念 -一些经验： +刚开始学习算法的时候，看了某大佬讲解回溯算法和 dfs 的区别： + +- **dfs** 关注点在 「节点」 +- **回溯** 关注点在 「树枝」 + +对应的代码如下： + +```js +// DFS 算法把「做选择」「撤销选择」的逻辑放在 for 循环外面 +var dfs = function (root) { + if (root == null) return + // 做选择 + console.log('我已经进入节点 ' + root + ' 啦') + for (var i in root.children) { + dfs(root.children[i]) + } + // 撤销选择 + console.log('我将要离开节点 ' + root + ' 啦') +} + +// 回溯算法把「做选择」「撤销选择」的逻辑放在 for 循环里面 +var backtrack = function (root) { + if (root == null) return + for (var i in root.children) { + // 做选择 + console.log('我站在节点 ' + root + ' 到节点 ' + root.children[i] + ' 的树枝上') + backtrack(root.children[i]) + // 撤销选择 + console.log('我将要离开节点 ' + root.children[i] + ' 到节点 ' + root + ' 的树枝上') + } +} +``` + +以上代码不要死记硬背，更不要被唬到了，想想一下二叉树的递归序，一切就都了然了 --- **不过是多叉树没明着写出来所有分支，改用了一个 for 循环罢了**。 + +--- + +后面在 B 站看了左神的算法课，左神说过这么一句话：国外根本就不存在什么回溯的说法，就是暴力递归。不知道此话的真假，抱着怀疑的态度，我问了下 chatGPT： + +> 本质区别 +> +> - dfs 就是沿着树的深度尽可能远的搜索，直到到达叶节点 +> - 回溯则是一种搜索策略，发现路径不符合条件或者找到解则返回上一步继续尝试其他路径，直到遍历完所有可能的路径或者找到解 + + + +dfs 在遍历树、图等等场景应用非常广泛，而回溯算法则更善于解决「排列组合」类的问题（排列有序，组合无序），本文主要练习一下回溯算法。 + +--- + +### 回溯练习-排列组合 + + -> 其实这种回溯，与 dfs 很相像，只不过回溯是遍历树枝，而 dfs 是遍历节点。 -> backtrack 中 for 循环以外都是节点操作位置，for 循环内是树枝的操作位置 - -另外涉及到递归都需要注意终止条件哦 👻。 - -### [39.组合总和](https://leetcode.cn/problems/combination-sum/) - -关键点： - -1. 无重复元素 -2. 元素可以重复选。 +#### lc.39 组合总和 ```js /** @@ -38,22 +84,35 @@ categories: [algorithm] * @return {number[][]} */ var combinationSum = function (candidates, target) { + /** + * 无重复元素，所以不用剪枝 + * 可以被重复选取，那么就是类似这么个树 + * 1 2 3 + * 1 2 3 1 2 3 1 2 3 + * ..... ..... .... + */ const res = [] const track = [] let sum = 0 - const backtrack = start => { + /** + * 仍然不要忘记定义递归 + * 输入：层级 level，输出 void; 在递归过程中把可行解塞入 res + * 结束条件，这道题比较明显 sum === target + */ + const backtrack = level => { if (sum === target) { - res.push([...track]) + res.push([...track]) // 注意拷贝一下 return } - if (sum > target) return - for (let i = start; i < candidates.length; ++i) { - const v = candidates[i] - sum += v - track.push(v) - backtrack(i) - sum -= v + if (sum > target) return // 结束条件不要忘了~ + // level 在这里的含义是1.在 level 层， 2.在候选数据 [level...end] 区间内做选择，通过保证元素的相对顺序，来避免重复的组合 + // 如果每次都从 0 开始，那么 可能会产生 [1,2] [2,1] 这样重复的组合，不过这对排列来说，是有用的 + for (let i = level; i < candidates.length; ++i) { + track.push(candidates[i]) + sum += candidates[i] + backtrack(i) // 可重复使用，i + 1 则是在下一层排除了自己 track.pop() + sum -= candidates[i] } } backtrack(0) @@ -61,39 +120,38 @@ var combinationSum = function (candidates, target) { } ``` -### [40.组合总和 II](https://leetcode.cn/problems/combination-sum-ii/) +此题完全弄懂之后，排列组合就都是纸老虎了。 -关键点： +#### lc.40 组合总和 II -1. 有重复元素 -2. 不可以重复选择 -3. 要求 不能包含重复的组合 + ```js /** + * 与 lc.39 唯二不同，1.有重复元素，2.不能复用元素 * @param {number[]} candidates * @param {number} target * @return {number[][]} */ var combinationSum2 = function (candidates, target) { - candidates.sort((a, b) => a - b) const res = [] const track = [] let sum = 0 - const backtrack = start => { + candidates.sort((a, b) => a - b) + const backtrack = level => { if (sum === target) { res.push([...track]) return } - for (let i = start; i < candidates.length; ++i) { - if (sum + candidates[i] > target) continue - if (i > start && candidates[i] === candidates[i - 1]) continue - const v = candidates[i] - track.push(v) - sum += v - backtrack(i + 1) + if (sum > target) return + for (let i = level; i < candidates.length; ++i) { + // 因为元素有重复的，所以需要先进行 「排序」，然后进行剪枝 + if (i > level && candidates[i] === candidates[i - 1]) continue + track.push(candidates[i]) + sum += candidates[i] + backtrack(i + 1) // 不能复用元素，下一层 level 不能包扩 i 自身 + sum -= candidates[i] track.pop() - sum -= v } } backtrack(0) @@ -101,14 +159,41 @@ var combinationSum2 = function (candidates, target) { } ``` -### [77.组合](https://leetcode.cn/problems/combinations/) +#### lc.216 组合总和 III -这道题没有直接说出是否有重复元素，是否可以复选需要我们自己审题提炼。 +```js +/** + * @param {number} k + * @param {number} n + * @return {number[][]} + */ +var combinationSum3 = function (k, n) { + const res = [] + const track = [] + let sum = 0 + const backtrack = level => { + if (sum === n && track.length === k) { + res.push([...track]) + return + } + if (sum > n) return + for (let i = level; i < 10; ++i) { + if (track.length > k) continue + track.push(i) + sum += i + backtrack(i + 1) + track.pop() + sum -= i + } + } + backtrack(1) + return res +} +``` -关键点： +#### lc.77 组合 -1. 无重复元素 -2. 不可以复选 + ```js /** @@ -119,12 +204,12 @@ var combinationSum2 = function (candidates, target) { var combine = function (n, k) { const res = [] const track = [] - const backtrack = start => { + const backtrack = level => { if (track.length === k) { res.push([...track]) return } - for (let i = start; i <= n; ++i) { + for (let i = level; i <= n; ++i) { track.push(i) backtrack(i + 1) track.pop() @@ -135,12 +220,13 @@ var combine = function (n, k) { } ``` -### [78.子集](https://leetcode.cn/problems/subsets/) +索然无味的一题~ -关键点： +--- + +#### lc.78 子集 -1. 无重复元素 -2. 不可复选 + ```js /** @@ -148,13 +234,21 @@ var combine = function (n, k) { * @return {number[][]} */ var subsets = function (nums) { - const res = [] + // root + // 1 2 3 + // 2 3 3 + // 3 + const res = [[]] const track = [] - const backtrack = start => { - res.push([...track]) + const backtrack = level => { + // res.push([...track]) 在这里加入 是另一种无需 res 提前 [[]] + // 此处是在「节点」操作区 if (track.length === nums.length) return - for (let i = start; i < nums.length; ++i) { + for (let i = level; i < nums.length; ++i) { track.push(nums[i]) + // 在这里加入 需要 res 需要提前加一个空 [] + // 此处是 「树枝」操作区 + res.push([...track]) backtrack(i + 1) track.pop() } @@ -164,14 +258,9 @@ var subsets = function (nums) { } ``` -> 这道题的递归结束条件，看似没有设置，其实是通过 `start` 来控制的，若 `start >= nums.length` 是不会进入 `for` 循环的，也就结束的递归 - -### [90.子集 II](https://leetcode.cn/problems/subsets-ii/) +#### lc.90 子集 II -关键点： - -1. 有重复元素 -2. 不可重复选择 + ```js /** @@ -179,14 +268,14 @@ var subsets = function (nums) { * @return {number[][]} */ var subsetsWithDup = function (nums) { - nums.sort((a, b) => a - b) const res = [] const track = [] - const backtrack = start => { + nums.sort((a, b) => a - b) + const backtrack = level => { res.push([...track]) - if (track.length === nums.length) return - for (let i = start; i < nums.length; ++i) { - if (i > start && nums[i] === nums[i - 1]) continue + if (level === nums.length) return + for (let i = level; i < nums.length; ++i) { + if (i > level && nums[i] === nums[i - 1]) continue track.push(nums[i]) backtrack(i + 1) track.pop() @@ -197,12 +286,16 @@ var subsetsWithDup = function (nums) { } ``` -### [46.全排列](https://leetcode.cn/problems/permutations/) +--- -关键点： +#### lc.46 全排列 -1. 无重复元素 -2. 不可复选 + + +排列和组合最大的区别是： + +- 组合无序，[1,2]和 [2,1] 是同一个组合，所以需要 level 来控制 +- 排序有序，所以每次都是从 level-0 开始，但是不能重复使用元素，就需要一个 「used」(可以为一个简单的 boolean[]数组，也可以为一个栈) 来进行剪枝操作 ```js /** @@ -212,20 +305,19 @@ var subsetsWithDup = function (nums) { var permute = function (nums) { const res = [] const track = [] - const uesd = [] + const used = [] const backtrack = () => { if (track.length === nums.length) { res.push([...track]) return } for (let i = 0; i < nums.length; ++i) { - const v = nums[i] - if (uesd.includes(v)) continue - track.push(v) - uesd.push(v) + if (used[i]) continue // 剪枝 + track.push(nums[i]) + used[i] = true backtrack() track.pop() - uesd.pop() + used[i] = false } } backtrack() @@ -233,12 +325,9 @@ var permute = function (nums) { } ``` -### [47.全排列 II](https://leetcode.cn/problems/permutations-ii/) +#### lc.47 全排列 II -关键点： - -1. 有重复元素 -2. 不可复选 + ```js /** @@ -246,18 +335,18 @@ var permute = function (nums) { * @return {number[][]} */ var permuteUnique = function (nums) { - nums.sort((a, b) => a - b) const res = [] const track = [] const used = [] + nums.sort((a, b) => a - b) const backtrack = () => { if (track.length === nums.length) { res.push([...track]) return } for (let i = 0; i < nums.length; ++i) { - if (used[i]) continue - if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue // 新的剪枝逻辑 就是 保证相同元素的顺序固定不变 + if (used[i]) continue // 去除自身剪枝 + if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue // 关键 track.push(nums[i]) used[i] = true backtrack() @@ -269,3 +358,534 @@ var permuteUnique = function (nums) { return res } ``` + +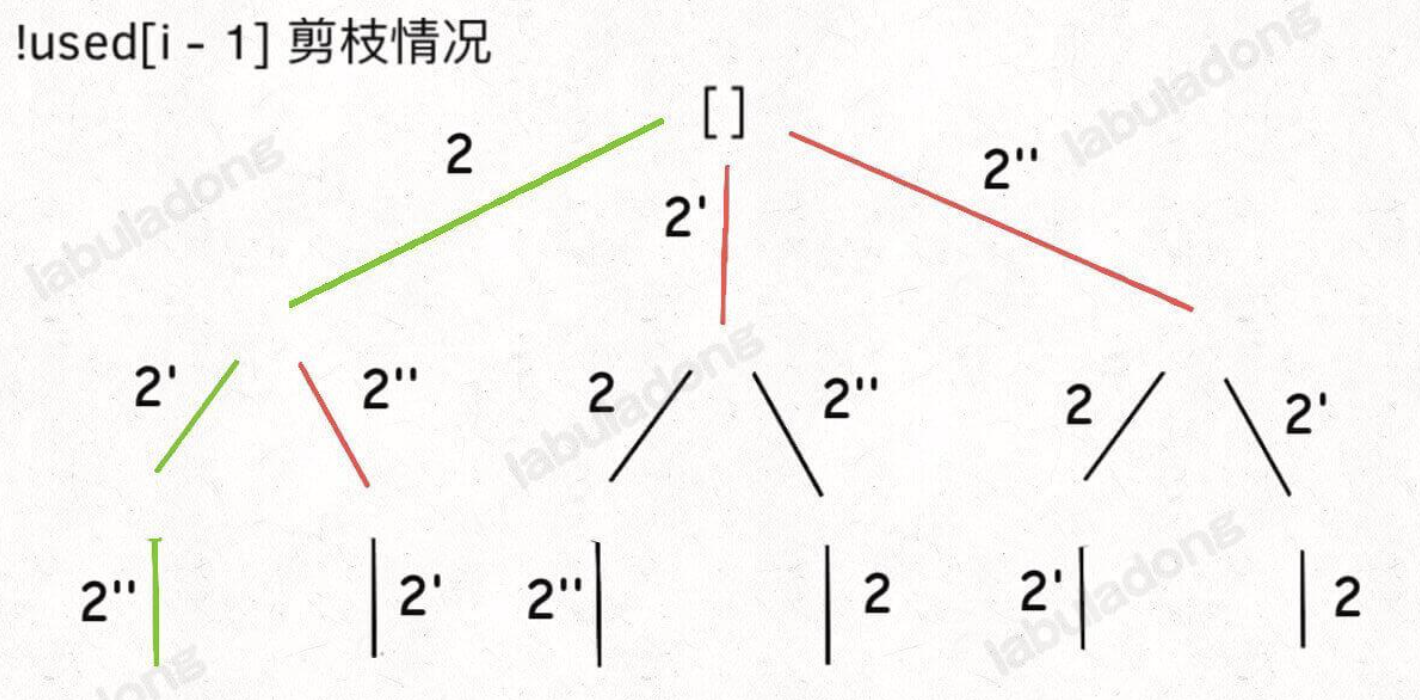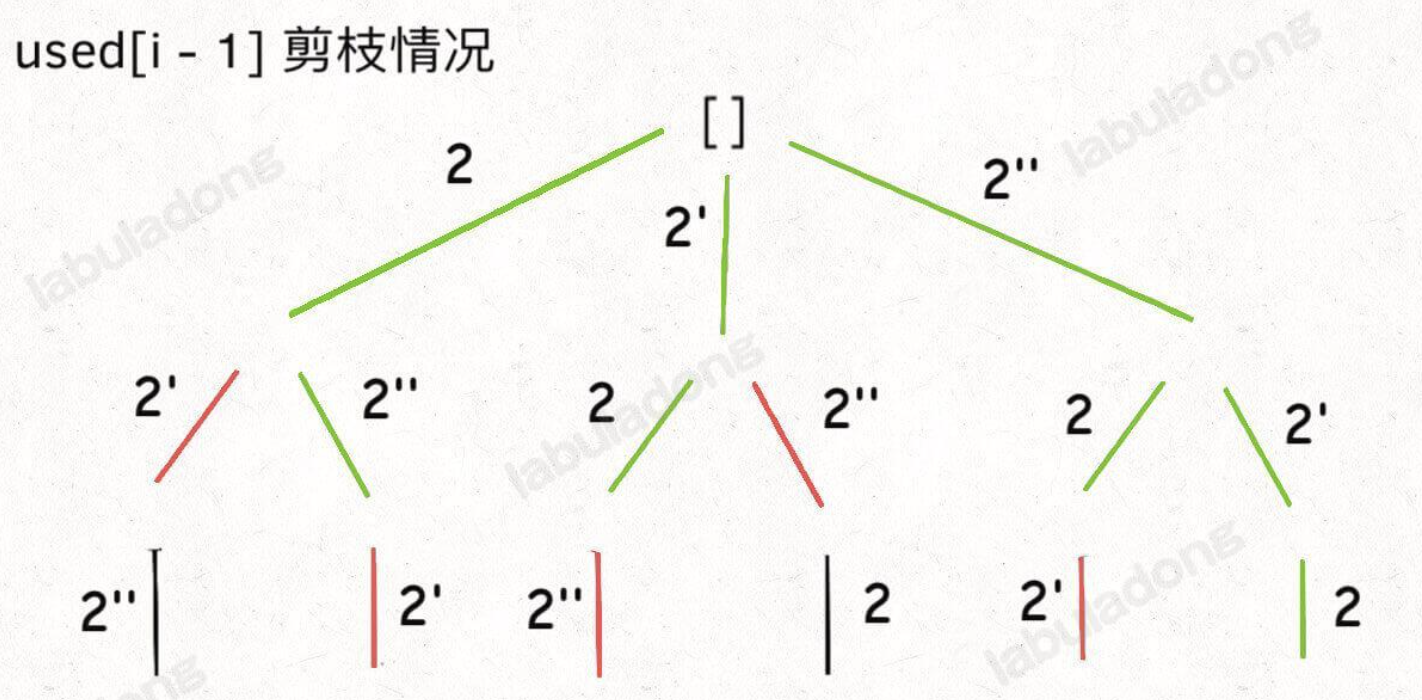上方 `!used[i-1]` 是为了去除重复的排列，当同一层前后两个元素相同时，如果前一个元素没有使用，那么就 continue，这样做的结果就是会让 `[2,2',2'']` 这样的数组保持固定的顺序，即 2 一定在 2' 前，2' 一定在 2'' 前。如果改为 `used[i-1]` 也能得到去重的效果，就是固定顺序为 2'' -> 2' -> 2，但是剪枝的效率会大大折扣，可以参考 labuladong 大佬的示意图理解。 + +
+ + +
+ +### 经典题 + +#### lc.51 N 皇后 + +```js +/** + * @param {number} n + * @return {string[][]} + */ +var solveNQueens = function (n) { + // 这道题是二维的 track，所以得先初始化一个二维棋盘再说 + // 同时类似组合，需要 level 来控制深度；又似排列，需要每次都遍历每一行的每一个 + const res = [] + const board = Array.from(Array(n), () => Array(n).fill('.')) + const backtrack = level => { + if (level === n) { + res.push([...board.map(item => item.join(''))]) + return + } + for (let i = 0; i < n; ++i) { + //剪枝操作 + if (!isValid(board, level, i)) continue + board[level][i] = 'Q' + backtrack(level + 1) + board[level][i] = '.' + } + } + backtrack(0) + return res +} +/** + * 判断是否合格，因为是从上往下铺的，所以只判断左上，上，右上即可 + */ +function isValid(board, row, col) { + for (let i = 0; i < row; ++i) { + if (board[i][col] === 'Q') return false + } + for (let i = row - 1, j = col - 1; i >= 0; --i, --j) { + if (board[i][j] === 'Q') return false + } + for (let i = row - 1, j = col + 1; i >= 0; --i, ++j) { + if (board[i][j] === 'Q') return false + } + return true +} +``` + + + +#### lc.698 划分为 k 个相等的子集 + +给你输入一个数组 nums 和一个正整数 k，请你判断 nums 是否能够被平分为元素和相同的 k 个子集。 + +典中典，也是深入理解回溯的绝佳好题，必会必懂。 + +```js +// lc.416 分割两个等和子集，可以用动态规划去做，本文是 k 个子集，得上 dfs +// lc.78 是求出所有子集，这道题是固定了子集的数量，去分配 +/** + * @param {number[]} nums + * @param {number} k + * @return {boolean} + */ +var canPartitionKSubsets = function (nums, k) { + if (k > nums.length) return false + const sum = nums.reduce((a, b) => a + b) + if (sum % k !== 0) return false + + const bucketTarget = sum / k + const used = [] + // 定义递归：输入 k 号桶, 每个数字不能重复使用，所以从 level 层开始选择 + // 输出：k 号桶，是否应该把 nums[level] 加入进来 + const backtrack = (k, level, bucketSum) => { + if (k === 0) return true // 所有桶装满了 + // 一个桶装满了，继续下一个桶 + if (bucketSum === bucketTarget) { + return backtrack(k - 1, 0, 0) // 从 0 层 0 sum 重新开始累加和 + } + for (let i = level; i < nums.length; ++i) { + if (used[i]) continue // 剪枝，被用过啦 + if (nums[i] + bucketSum > bucketTarget) continue // 这个数装不得，装了就超载~ + used[i] = true + bucketSum += nums[i] + if (backtrack(k, level + 1, bucketSum)) return true // 递归下一个数字是否加入桶 + used[i] = false + bucketSum -= nums[i] + } + return false + } + return backtrack(k, 0, 0) +} +/** + * 上方代码，逻辑上是没有问题的，但是效率低下，跑力扣的测试用例会超时 + * + * 优化自然是可以想到 memo 缓存，再就是我没想到的 used 改为位运算[捂脸]。。。 + */ +var canPartitionKSubsets = function (nums, k) { + if (k > nums.length) return false + const sum = nums.reduce((a, b) => a + b) + if (sum % k !== 0) return false + + const bucketTarget = sum / k + let used = 0 // 使用位图技巧 + const backtrack = (k, level, bucketSum, memo) => { + if (k === 0) return true + if (bucketSum === bucketTarget) { + const nextBucket = backtrack(k - 1, 0, 0, memo) + memo.set(used, nextBucket) + return nextBucket + } + if (memo.has(used)) { + // 避免冗余计算 + return memo.get(used) + } + for (let i = level; i < nums.length; ++i) { + // 判断第 i 位是否是 1 + if (((used >> i) & 1) === 1) { + continue // nums[i] 已经被装入别的桶中 + } + if (nums[i] + bucketSum > bucketTarget) continue + used |= 1 << i // 将第 i 位置为 1 + bucketSum += nums[i] + if (backtrack(k, level + 1, bucketSum, memo)) return true + used ^= 1 << i // 使用异或运算将第 i 位恢复 0 + bucketSum -= nums[i] + } + return false + } + return backtrack(k, 0, 0, new Map()) +} +``` + +这道题，我是觉得挺有难度的。。。位运算俺着实没想到啊 😭 + + + +> 推荐阅读：[「labuladong 球盒模型」](https://labuladong.online/algo/practice-in-action/two-views-of-backtrack-2/) + +#### lc.22 括号生成 + +```js +/** + * @param {number} n + * @return {string[]} + */ +var generateParenthesis = function (n) { + // 当出现右括号数量 > 左括号数量时，无效 + const res = [] + const track = [] + const backtrack = (l, r) => { + if (l > r) return + if (l < 0 || r < 0) return + if (l === 0 && r === 0) { + res.push([...track].join('')) + return + } + /** 之前可选择的是很多个，这里就两个直接摊开写方便 */ + track.push('(') + backtrack(l - 1, r) + track.pop() + track.push(')') + backtrack(l, r - 1) + track.pop() + } + backtrack(n, n) + return res +} +``` + +#### lc.37 解数独 hard + +建议先做岛屿类问题，再做此题。 + +```js +/** + * 根据题意，一开始很容易写出这样子的代码，但是此刻 dfs 是什么意思呢？应该是一个探测的过程 + * 也就是说 -- 此处有回溯！与岛屿类问题 flood fill 算法不同的是：flood fill 它直接就 flush 掉了找到的陆地 + * 而此处的 dfs 是在不断探测的，是要走回头路的，所以这两个 for 循环是在 dfs 之内的，即： + * dfs() {for(for(选择 dfs 撤销选择))} + */ +var solveSudoku = function (board) { + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (board[i][j] === '.') { + for (let k = 1; k <= 9; ++k) { + dfs(grid, i, j, k.toString()) + } + } + } + } +} +/** 开奖 */ +/** + * @param {character[][]} board + * @return {void} Do not return anything, modify board in-place instead. + */ +var solveSudoku = function (board) { + dfs(board) +} +function dfs(grid) { + for (let i = 0; i < 9; ++i) { + for (let j = 0; j < 9; ++j) { + if (grid[i][j] === '.') { + for (let k = 1; k <= 9; ++k) { + // 重点是剪枝 + if (!isValid(grid, i, j, k.toString())) continue + grid[i][j] = k.toString() + if (dfs(grid)) return true // 找到一种可行解 直接结束 + grid[i][j] = '.' + } + return false // 9 个数字都不行 + } + } + } + return true // 遍历完没有返回 false，说明找到了一组合适棋盘位置了 +} +function isValid(grid, row, col, tryVal) { + for (let i = 0; i < 9; ++i) { + if (grid[row][i] === tryVal) return false + if (grid[i][col] === tryVal) return false + } + + const startRow = Math.floor(row / 3) * 3 + const startCol = Math.floor(col / 3) * 3 + for (let i = startRow; i < startRow + 3; ++i) { + for (let j = startCol; j < startCol + 3; ++j) { + if (grid[i][j] === tryVal) return false + } + } + + return true +} +``` + +#### lc.200 岛屿的数量 + +首先考验的是 dfs 遍历二维数组的能力。 + +```js +/** + * 在二维矩阵中的 dfs --- for{for{dfs}} + */ +function dfs(matrix, i, j, visited) { + if (i < 0 || j < 0 || i >= m || j >= n) return + /** 进节点 */ + if (visited[i][j]) return + visited[i][j] = true + /** 上下左右遍历 */ + dfs(matrix, i - 1, j) + dfs(matrix, i + 1, j) + dfs(matrix, i, j - 1) + dfs(matrix, i, j + 1) + /** 出节点 */ +} + +/** 此外有方向数组的技巧 */ +const dirs = [ + [-1, 0], + [1, 0], + [0, -1], + [0, 1] +] +// 把上方的四个 dfs 配合 dirs 改为 for 循环即可 +for (var d of dirs) { + const next_i = i + d[0] + const next_j = j + d[1] + dfs(matrix, next_i, next_j, visited) +} +``` + +```js +/** + * @param {character[][]} grid + * @return {number} + */ +var numIslands = function (grid) { + let res = 0 + const m = grid.length + const n = grid[0].length + const visited = Array.from(Array(m), () => Array(n).fill(false)) + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + // 从某个陆地节点开始 detect + if (grid[i][j] === '1') { + res++ + dfs(grid, i, j, visited) + } + } + } + return res +} +function dfs(grid, i, j, visited) { + const m = grid.length + const n = grid[0].length + if (i < 0 || j < 0 || i >= m || j >= n) return + if (grid[i][j] === '0') return + grid[i][j] = '0' // 淹没土地 + dfs(grid, i - 1, j, visited) + dfs(grid, i + 1, j, visited) + dfs(grid, i, j - 1, visited) + dfs(grid, i, j + 1, visited) +} +``` + +> 这种“淹掉岛屿”的 dfs 算法有自己的名字 --- [「经典的 Flood fill 算法」](https://zh.wikipedia.org/wiki/Flood_fill)，这样可以不用维护 visited 数组。如果题目要求不能修改原数组，那么还是用 visited 去做，就此题而言具体就是多两步操作，一个是在 res++ 前判断是否 visit 过，另一个就是在每次 dfs 前判断是否 visit 过。 + +_另外此题还可以使用 BFS 和 并查集 解决_ + + + +#### lc.695 岛屿的最大面积 + +```js +/** + * @param {number[][]} grid + * @return {number} + */ +var maxAreaOfIsland = function (grid) { + let maxArea = 0 + const m = grid.length + const n = grid[0].length + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (grid[i][j] === 1) { + maxArea = Math.max(maxArea, dfs(grid, i, j)) + } + } + } + return maxArea +} +// 继续 flood fill +function dfs(grid, i, j) { + const m = grid.length + const n = grid[0].length + if (i < 0 || j < 0 || i >= m || j >= n) return 0 + if (grid[i][j] === 0) return 0 + grid[i][j] = 0 + return dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1) + 1 +} +``` + + + +#### lc.1020 飞地的数量 + +```js +/** + * @param {number[][]} grid + * @return {number} + */ +var numEnclaves = function (grid) { + let res = 0 + const m = grid.length + const n = grid[0].length + // 先把四个边界的淹没掉 + for (let i = 0; i < m; ++i) { + dfs(grid, i, 0) + dfs(grid, i, n - 1) + } + for (let i = 0; i < n; ++i) { + dfs(grid, 0, i) + dfs(grid, m - 1, i) + } + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (grid[i][j] === 1) { + res++ + } + } + } + return res +} +function dfs(grid, i, j) { + const m = grid.length + const n = grid[0].length + if (i < 0 || j < 0 || i >= m || j >= n) return + if (grid[i][j] === 0) return + grid[i][j] = 0 + dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1) +} +``` + +#### lc.1254 统计封闭岛屿的数目 + +```js +/** + * @param {number[][]} grid + * @return {number} + */ +var closedIsland = function (grid) { + let res = 0 + const m = grid.length + const n = grid[0].length + for (let i = 0; i < m; ++i) { + dfs(grid, i, 0) + dfs(grid, i, n - 1) + } + for (let j = 0; j < n; ++j) { + dfs(grid, 0, j) + dfs(grid, m - 1, j) + } + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (grid[i][j] === 0) { + res++ + dfs(grid, i, j) + } + } + } + return res +} +function dfs(grid, i, j) { + const m = grid.length + const n = grid[0].length + if (i < 0 || j < 0 || i >= m || j >= n) return + if (grid[i][j] === 1) return + grid[i][j] = 1 + dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1) +} +``` + +#### lc.1905 统计子岛屿 + +这道题需要稍微思考一下，同样大小的 grid，统计 grid2 中的子岛屿，直接遍历是不太好操作的，得先排除掉非子岛屿，然后再统计。什么是非子岛屿，那就是在 grid 中是陆地，但是在 grid1 中是海洋，直接淹掉，这样最后再遍历的时候剩下的就都是子岛屿啦。 + +```js +/** + * @param {number[][]} grid1 + * @param {number[][]} grid2 + * @return {number} + */ +var countSubIslands = function (grid1, grid2) { + let res = 0 + const m = grid2.length + const n = grid2[0].length + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (grid2[i][j] === 1 && grid2[i][j] !== grid1[i][j]) { + dfs(grid2, i, j) + } + } + } + for (let i = 0; i < m; ++i) { + for (let j = 0; j < n; ++j) { + if (grid2[i][j] === 1) { + res++ + dfs(grid2, i, j) + } + } + } + return res +} +function dfs(grid, i, j) { + const m = grid.length + const n = grid[0].length + if (i < 0 || j < 0 || i >= m || j >= n) return + if (grid[i][j] === 0) return + grid[i][j] = 0 + dfs(grid, i - 1, j) + dfs(grid, i + 1, j) + dfs(grid, i, j - 1) + dfs(grid, i, j + 1) +} +``` + +这道题自然也是可以使用 「并查集」来解决，后序并查集章节会详细使用。 + +--- + +> 请注意，本文所有的回溯函数，都使用了闭包的特性，如果不使用闭包，把需要的参数变为回溯函数的入参即可。 + +我亦无他，唯手熟尔！peace~ diff --git "a/content/posts/algorithm/z-others/\344\275\215\350\277\220\347\256\227.md" "b/content/posts/algorithm/z-others/\344\275\215\350\277\220\347\256\227.md" index ff63740..301adfc 100644 --- "a/content/posts/algorithm/z-others/\344\275\215\350\277\220\347\256\227.md" +++ "b/content/posts/algorithm/z-others/\344\275\215\350\277\220\347\256\227.md" @@ -100,6 +100,8 @@ public static int findOdd(int[] arr) { ### 进阶：一组数，只有 2 个数出现了一次，其他都是偶数次，找出这 2 个数 +lc.260 + ```java /** * 根据上一题可以很容易得到 a^b 的值，问题在于怎么找到这两个数字