-
Notifications
You must be signed in to change notification settings - Fork 634
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
腾讯&leetcode611:有效三角形的个数 #93
Comments
|
本题可结合: 一起练习 解法:排序+双指针我们知道三角形的任意两边之和大于第三边,任意两边之差小于第三边,如果这三条边长从小到大为 解题思路: 先数组排序,排序完后,固定最长的边,利用双指针法判断其余边 以 以 判断
代码实现: let triangleNumber = function(nums) {
if(!nums || nums.length < 3) return 0
let count = 0
// 排序
nums.sort((a, b) => a - b)
for(let k = nums.length - 1; k > 1; k--){
let i = 0, j = k - 1
while(i < j){
if(nums[i] + nums[j] > nums[k]){
count += j - i
j--
} else {
i++
}
}
}
return count
}复杂度分析:
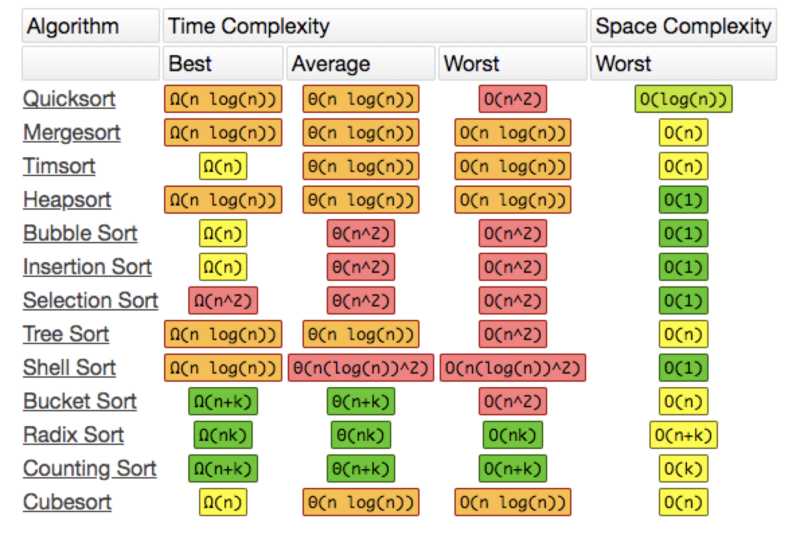
注意: 关于 在 V8 引擎 7.0 版本之后就舍弃了快速排序,因为它不是稳定的排序算法,在最坏情况下,时间复杂度会降级到 O(n2)。 而是采用了一种混合排序的算法:TimSort 。 这种功能算法最初用于Python语言中,严格地说它不属于以上10种排序算法中的任何一种,属于一种混合排序算法: 在数据量小的子数组中使用插入排序,然后再使用归并排序将有序的子数组进行合并排序,时间复杂度为 |
|
这个题目和三数之和雷同吧,只是将 a + b = c 的判定公式改成 a² + b² = c²。 |
判定公式是 任意两边之和大于第三边 |
|
count+=1 吧 怎么会是count += j-1 |
就是 |
感谢, 确实如此 之前看错了 |
给定一个包含非负整数的数组,你的任务是统计其中可以组成三角形三条边的三元组个数。
示例 1:
注意:
附赠leetcode地址:leetcode
The text was updated successfully, but these errors were encountered: