$ python3 main.py --block "basic" --epoch 75NOTE: on Colab Notebook use following command:
!git clone link-to-repo
%run main.py --block "basic" --epoch 75- He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. arXiv:1512.03385
The above paper focuses on improving the depth of deep neural networks while not compromising on accuracy.Vanilla Deep networks suffer from a problem which is named as degradation (completely different from over fitting) in this paper.Degradation causes vanilla networks to have increased training losses (as opposed to overfitting which causes lower training error) when the number of layers is increased.The authors of the paper have credited this to the inability of optimizing the the network effeciently.
I am writing this summary to help my understanding,as well as anyone who might read this,along with my implementation too.The link to the implementation can be found here
| (Fig.1) the degradation problem. |
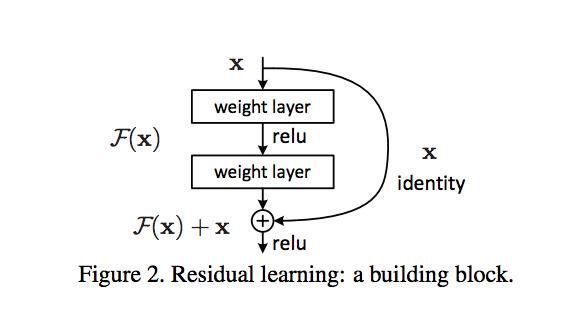
This paper aims to solve this issue by introducing a framework called "residual" framework which uses shortcuts to add input from previous layers to the current layer.This solves the problem of optimizing easily as it gives the gradients ability to "hop" over the layers.This,along with batch normalization can solve the problems of vanishing/exploding gradients effortlessly.
The inputs from the previous layers are added through either an identity mapping,if the input and output sizes are the same(thus requiring no extra parameters),or by padding the input with zeros(also not requiring extra parameters),or by using projections to match sizes with the ouptut.Sure enough,the paper quotes the same:
The dimensions of x and F must be equal in Eqn.(1). If this is not the case (e.g., when changing the input/output channels), we can perform a linear projection W s by the shortcut connections to match the dimensions:
The mathematical reasoning behind why this works is provided by the Universal approximator theorem which states,that given sufficient data and/or time,a neural network can approximate any function (under some assumptions).Another reason why this works is because it makes the layers approximate the zero function(as we go deeper) so that optimization can become easier(Compared to approxiamting identity functions).The paper quotes :
If one hypothesizes that multiple nonlinear layers can asymptoti cally approximate complicated functions(such as our hypothesis function H(X) , then it is equivalent to hypothesize that they can asymptotically approxi- mate the residual functions, i.e.,H(x) − x(assuming that the input and output are of the same dimensions). So rather than expect stacked layers to approximate H(x), we explicitly let these layers approximate a residual function F(x) := H(x) − x. The original function thus becomes F(x)+x. Although both forms should be able to asymptot- ically approximate the desired functions (as hypothesized), the ease of learning might be different.
 |
|---|
| (Fig.3) The architecture of a standard VGG network (bottom), a plain 34 layer network (middle) and a residual network (top). |
Both the plain and residual networks have lower flops (multiply-add) than VGG,though they are deeper.The method we'll be using in our implementation is to apply projections,whenever there is a mismatch of sizes(named as option B in paper),as opposed to identity mappings with zeros padded(option A),or using projections on all shortcuts(option C) As you can see in the residual network, individual "Basic Blocks" (named so because we have different block structures) make up the architecture, made up of two 3x3 convolution layers with BN applied after each layer.The down-sampling(Reduction in image-size) in between two layers is acheived through using a stride of 2 in the first layer of the block.
The paper also mentions of an architecture using the repetitve element as a "bottleneck block" as shown in the figure below.This can be implemented by simply replacing every basic block with a bottleneck block. The main advantage of bottleneck block is that it leads to lesser parameters and hence faster training and convergence.
| (Fig. 4) The two blocks in the model |
In our implementation of the residual network we will be using both the bottleneck and basic blocks and comparing results from both of them.We will be using the same architecture in the paper.Let's see what the paper has to say on this.
Note : One main difference(Might be a cause for un-SOTA-ish behavior) between our network and the paper's is that we dont have separate convolutional layers in between blocks to Down-Sample inputs.
The plain/residual architectures follow the form in Fig. 3 (middle/top). The network inputs are 32×32 images, with the per-pixel mean subtracted. The first layer is 3×3 convo- lutions. Then we use a stack of 6n layers with 3×3 convo- lutions on the feature maps(output size of image) of sizes {32, 16, 8} respectively, with 2n layers for each feature map size. The numbers of filters are {16, 32, 64} respectively. The subsampling is per- formed by convolutions with a stride of 2. The network ends with a global average pooling, a 10-way fully-connected layer, and softmax. There are totally 6n+2 stacked weighted layers. The following table summarizes the architecture:
| output map size | 32x32 | 16x16 | 8x8 |
|---|---|---|---|
| #filters | 16 | 32 | 64 |
| #layers | 2n+1 | 2n | 2n |
We'll be trying to implement the models in two ways :
- ResNet-32.
- No Dropout layers.
- Use Softmax in last layer
- use relu activation
- No learning rate schedulers .
- Basic Model trained for 90 epochs,Bottleneck Model for 80 epochs.
- ResNet-32.
- Softmax not used.
- Image Augmentation done.(Because model suffered from over-fitting)
- 2d-Droupout used with p=0.25 before last block.
- Use Celu activation with alpha=0.075 (had read here that celu,being differentiable has faster optimization).
- implemented learning rate decay with gamma=0.0025 applied after 50 and 70 epochs.
- Trained both Basic Model and Bottleneck model for 80 and 70 epochs.
A comparison in the number of parameters in both types of architecture gives us the following results(Taken from the torchsummary module) :
Total params: 468,826
Trainable params: 468,826
Non-trainable params: 0
Total params: 302,266
Trainable params: 302,266
Non-trainable params: 0
Bottle neck model has about 36% lesser parameters!! (This applies for both the implementations because a dropout layer requires no parameters)
- Training time for both of the models were about 1 hour $5 minutes.
- No percievable over-fitting was detected as test losses went down with train losses.
- this table sums up the results of Implmentation 1.
| Model type | Test Accuracy | Train Accuracy |
|---|---|---|
| Basic | 79.90% | 86% |
| Bottleneck | 77.010% | 85% |
(those $10$ epochs really made a difference!).
- Training time for both of the models were about 35 minutes (that's a whopper!)
- This decrease in execution time was mainly due the fact that I didn't use SoftMax,and used Celu.
- Over-fitting was detected,so dropout was neccessary to prevent it
- This table sums up the results of Implementation
$2$ :
| Model type | Test Accuracy | Train Accuracy |
|---|---|---|
| Basic | 85.530% | 95% |
| Bottleneck | 81.2% | 85.93% |
Clearly,The model accuracies weren't even close to SOTA (lol).I feel that this can be attributed to several reasons :
- Dropout functions can be implemented to further decrease overfitting on both the networks.
- Increasing the depth could provide more accuracy(That was the point of the paper,facepalm!) (Also,Gathering information from my peers showed this to be true indeed;ResNet-50's got you an accuracy of about 89%(No Dropout implemented,trained for only 60 epochs!)).
- Some of my peers had left the network to over-fit the data,thereby getting training accuracy of 99% and a test accuracy of 84%.(seems counter intuitive,but works!)(No Droupout,No Regularization,No Data-Augmentation)
- I still felt that increasing the epochs could lead to some improvement on the train-test accuracy.