A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.
When compared with a flat array of numbers, the Fenwick tree achieves a
much better balance between two operations: element update and prefix sum
calculation. In a flat array of n numbers, you can either store the elements,
or the prefix sums. In the first case, computing prefix sums requires linear
time; in the second case, updating the array elements requires linear time
(in both cases, the other operation can be performed in constant time).
Fenwick trees allow both operations to be performed in O(log n) time.
This is achieved by representing the numbers as a tree, where the value of
each node is the sum of the numbers in that subtree. The tree structure allows
operations to be performed using only O(log n) node accesses.
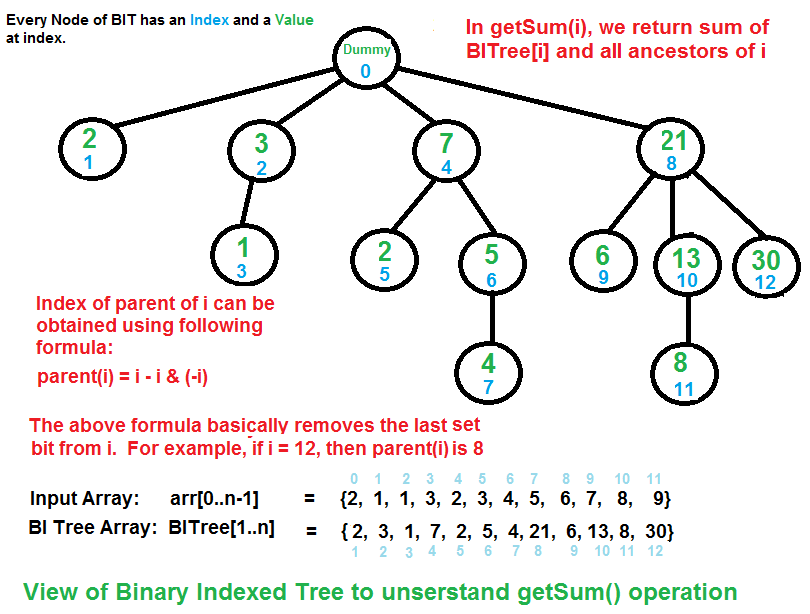
Binary Indexed Tree is represented as an array. Each node of Binary Indexed Tree
stores sum of some elements of given array. Size of Binary Indexed Tree is equal
to n where n is size of input array. In current implementation we have used
size as n+1 for ease of implementation. All the indexes are 1-based.
On the picture below you may see animated example of
creation of binary indexed tree for the
array [1, 2, 3, 4, 5] by inserting one by one.