LeetCode 53最大子序列和.md

LeetCode 53最大子序列和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

使用dp的方法就是O(n)的方法。如果dp[i]表示以第i个结尾的最大序列和，而这个dp的状态方程为：

dp[0]=a[0]
dp[i]=max(dp[i-1]+a[i],a[i])

也不难解释，如果以前一个为截至的最大子序列和大于0，那么就连接本个元素，否则本个元素就自立门户。

实现代码为：

public int maxSubArray(int[] nums) {
        int dp[]=new int[nums.length];
        int max=nums[0];
        dp[0]=nums[0];
        for(int i=1;i<nums.length;i++)
        {
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            if(dp[i]>max)
                max=dp[i];
        }
        return max;
    }

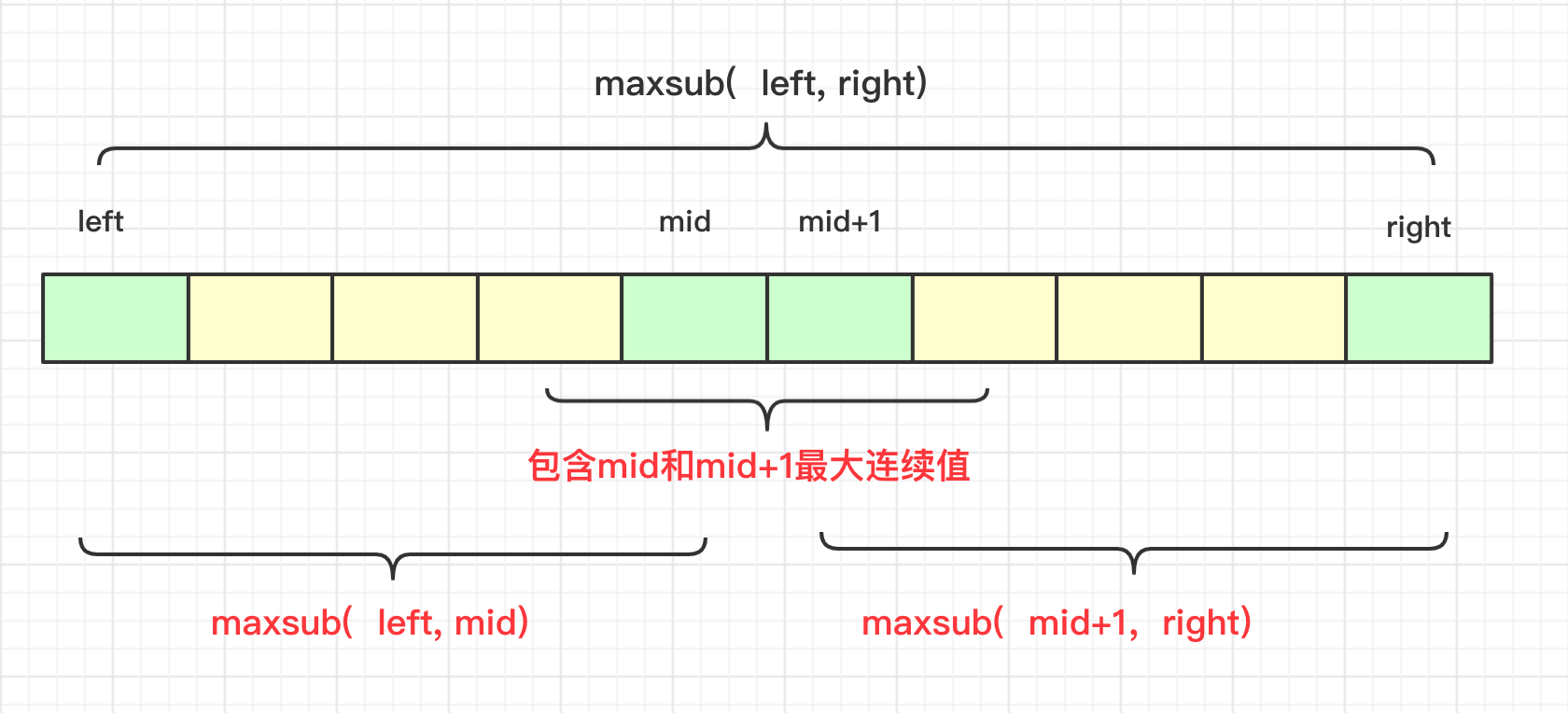
至于分治算法，这题复杂度dp为O(n),分治为O(nlogn).并不算快，而分治主要运用递归的过程先分再和，如果当然函数为maxsub(int nums[],int left,int right)最大的可能在以下三种情况产生： 其中中间部分就是分别向左向右进行拓展取最大了。ac代码为(2ms)：

public int maxSubArray(int[] nums) {

    int max=maxsub(nums,0,nums.length-1);
    return max;
}
int maxsub(int nums[],int left,int right)
{
    if(left==right)
        return  nums[left];
    int mid=(left+right)/2;
    int leftmax=maxsub(nums,left,mid);
    int rightmax=maxsub(nums,mid+1,right);

    int midleft=nums[mid];
    int midright=nums[mid+1];
    int team=0;
    for(int i=mid;i>=left;i--)
    {
        team+=nums[i];
        if(team>midleft)
            midleft=team;
    }
    team=0;
    for(int i=mid+1;i<=right;i++)
    {
        team+=nums[i];
        if(team>midright)
            midright=team;
    }
    int max=midleft+midright;//中间的最大值
    if(max<leftmax)
        max=leftmax;
    if(max<rightmax)
        max=rightmax;
    return  max;
}

结语

原创不易，bigsai请你帮两件事帮忙一下:

1. star支持一下， 您的肯定是我在平台创作的源源动力。

2. 微信搜索「bigsai」，关注我的公众号，不仅免费送你电子书，我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。

记得关注、咱们下次再见！