大家好,我是bigsai。
拓扑排序,很多人都可能听说但是不了解的一种算法。不知者大多会提出这样的疑问:
这是某种排序算法?这好像是一种图论算法?图也能排序?
非线性结构在传统意义上确实不太好排序,而拓扑排序它是对有向图的顶点排成一个线性序列。并且不一定唯一。
什么是拓扑排序?
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
拓扑排序有何作用?
拓扑排序的应用其实还是蛮多的,拓扑排序在一些工程有多道工序时候可以获取一个有效的加工顺序、还有些游戏里的任务成就必须满足一个符合的拓扑排序才能解锁下一关、还有一些项目或者环境的依赖关系集……
当然上面的例子可能不够具体,离我们稍微近一点的就是课程学习上,比如你学习数据结构之前基本要学习C或者C++这门课,因为数据结构中需要懂和会用C++的代码;学习操作系统、计算机网络之前要学习数据结构这门课,因为里面涉及到很多数据结构和算法;学习Java Web开发前要学习JavaSE和HTML这两门课;不同院校课程安排截然不同但均能很好的连接起来,就是因为安排的课程满足一个拓扑排序。
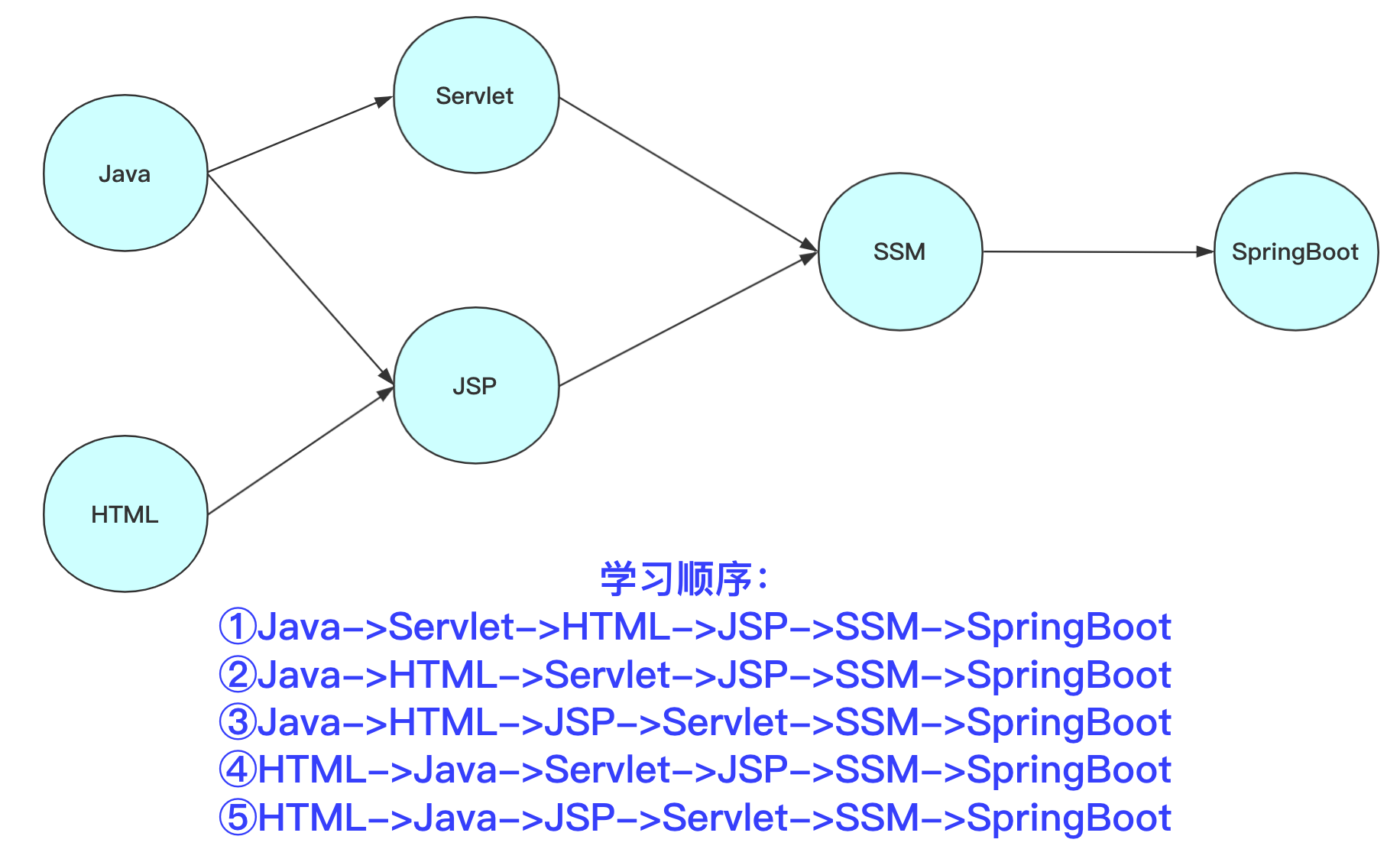
拓扑排序还是不能理解?我举个更详细的例子,学习Java系列的教程部分,可能有下面这个顺序:
| 代号 | 科目 | 学前需掌握 |
|---|---|---|
| A1 | JavaSE | |
| A2 | HTML | |
| A3 | JSP | A1,A2 |
| A4 | Servlet | A1 |
| A5 | SSM | A3,A4 |
| A6 | SpringBoot | A5 |
| 就比如学习Java系类(部分)从Java基础,到JSP/Servlet,到SSM,到SpringBoot,SpringCloud等是个循序渐进、且有前提依赖的过程。在JSP学习要首先掌握Java基础和HTML基础。学习框架要掌握JSP/Servlet和JDBC之类才行。那么,这个学习过程即构成一个拓扑序列。当然这个序列也不唯一,你可以对不关联的学科随意选择顺序(比如Html和Java可以随便先开始哪一个)。 |
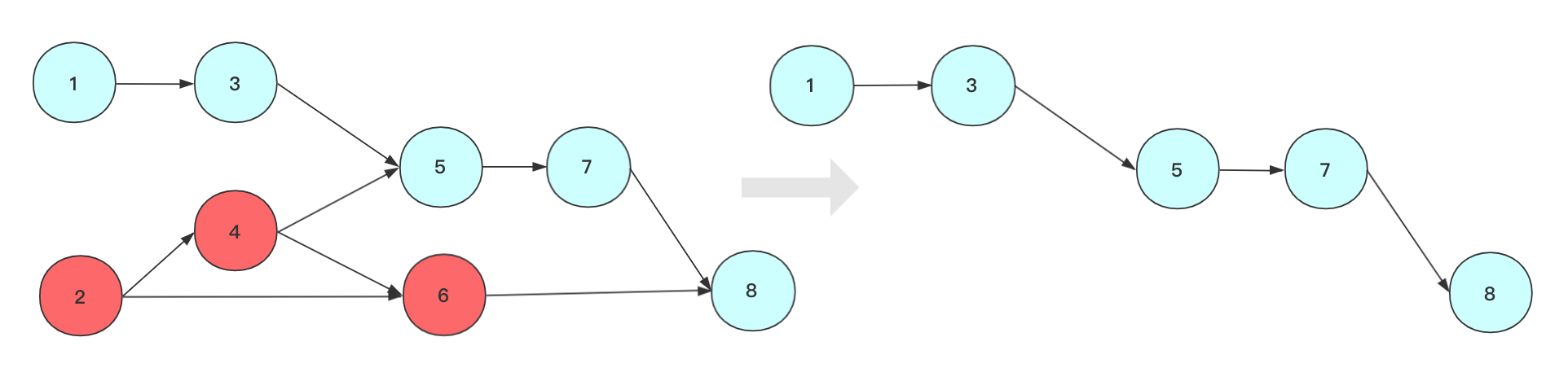
那上述序列可以简单表示为:
这五种均为可以选择的学习方案,对课程安排可以有参考作用,这五个都是上面有向无环图(DAG)的拓扑序列,只是小的选择的策略不同(先学Java或者先学HTML不要紧,但是要满足整个顺序要求),不影响满足规则顺序!
对于拓扑排序,还有一些比较专业的名词需要铭记:
DAG:有向无环图 AOV网:数据在顶点,顶点表示活动,边表示活动的先后关系,可以理解为一种面向对象。 AOE网:数据在边上,顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间,可以理解为面向过程。
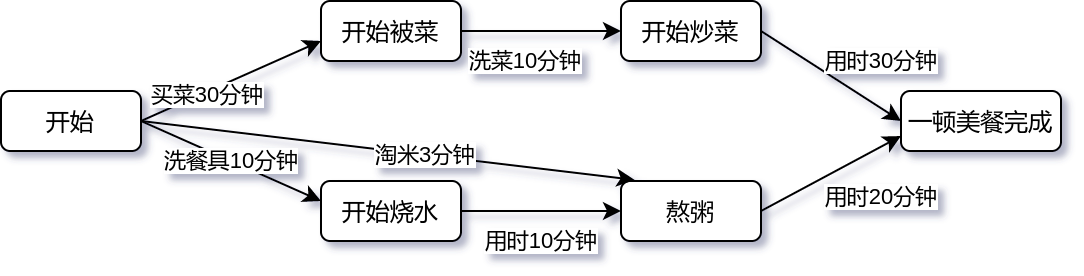
很多人不知道AOE网干啥用的,拓扑排序是解决一个工程能否顺序进行的问题,但有时还需解决工程完成需要的最短时间。而AOE经常使用在求关键路径中(这里就先不进行详细介绍内容和算法了),图片来源https://www.cnblogs.com/svod5306/p/14723338.html)。
我们今天讲的拓扑排序就是在AOV中找到不破坏图结构的序列,对于有向无环图,需要注意一下图中:若A在B前面,则不存在B在A前面的路径(不能成环)。图中两个相邻节点在拓扑序列中只需要满足前后关系而不一定需要相邻(节点只需满足相对的前后关系,所以拓扑排序并不一定唯一)。
上面简单的介绍了拓扑排序,下面详细讲讲拓扑排序的求法。
1.从DAG图中找到一个没有前驱的顶点输出。可以遍历入度为0的节点,也可以用优先队列维护。
2.删除以这个点为起点的边。删除一条边,其指向节点的入度减1,这样为了找到下个没有前驱节点的顶点。
3.重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环!
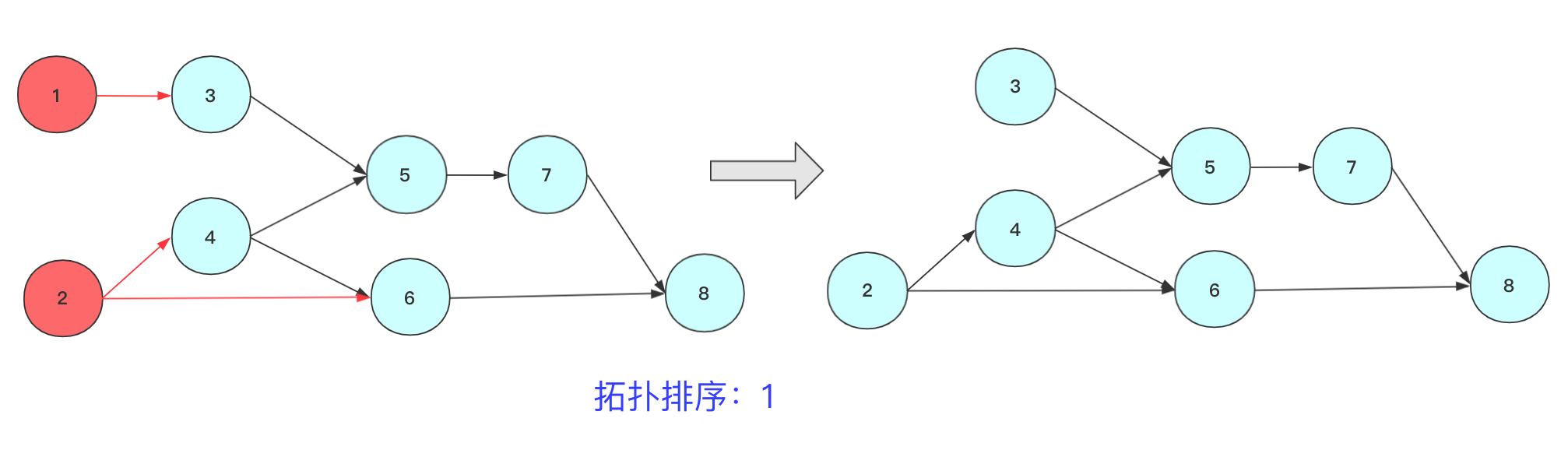
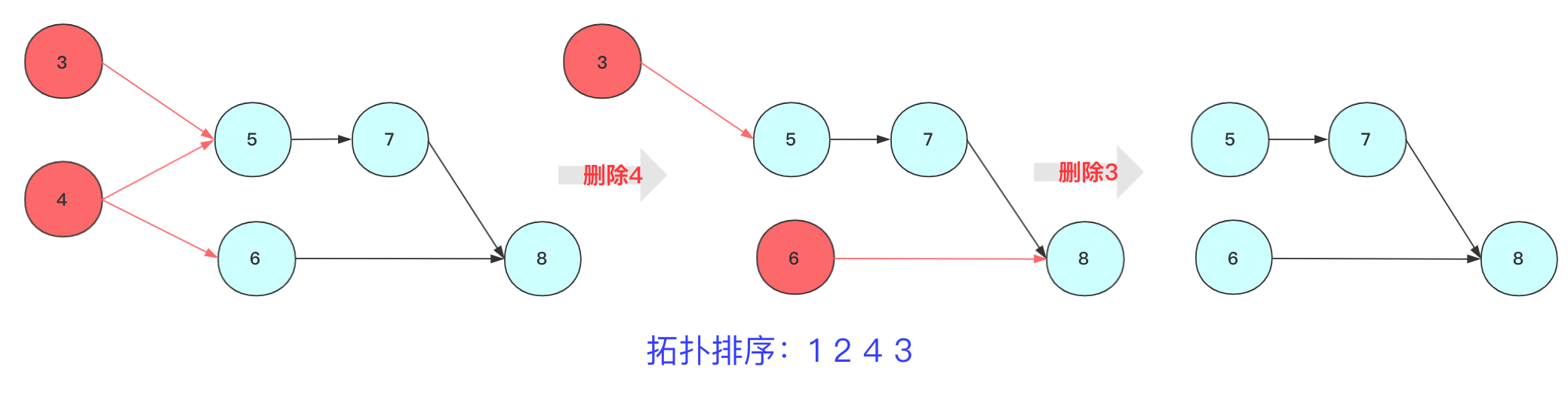
对于上图的简单序列,可以简单描述步骤为:
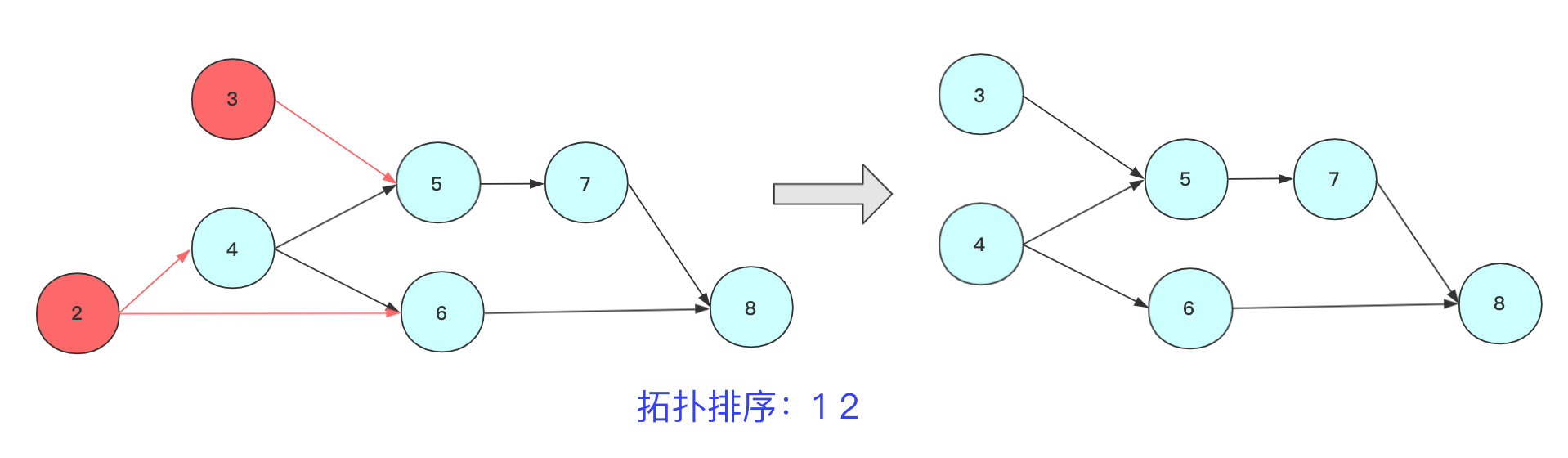
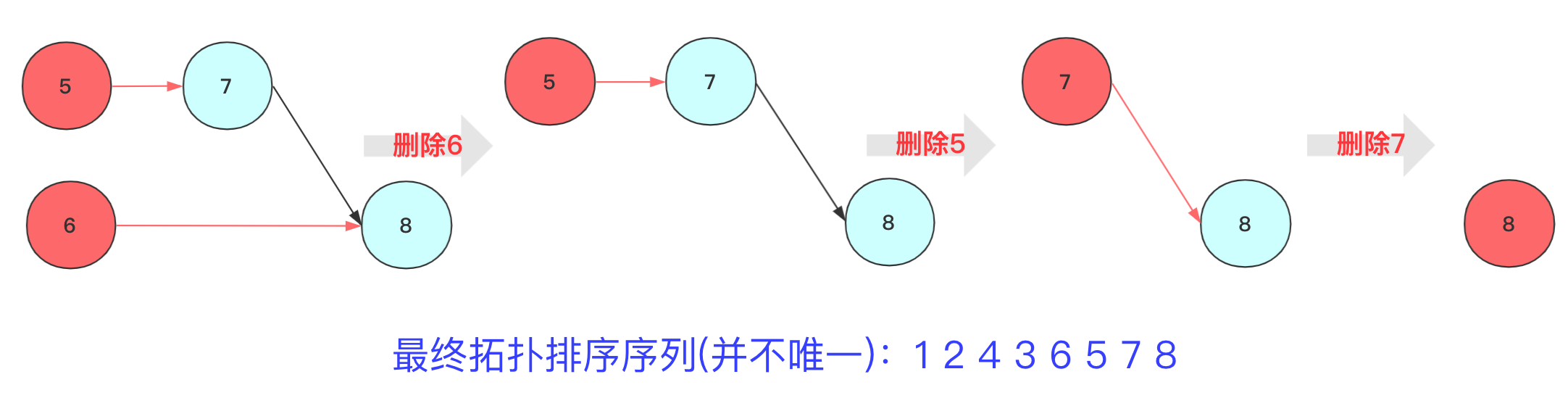
step2(这里进行两步):删除节点3(或者4)及其指向的边,将节点输出,紧接着删除节点3(或者6)其指向的边,将节点输出。
这样就完成一次拓扑排序流程,得到一个拓扑序列,但是这个序列并不唯一,从算法执行过程中也看到有很多选择方案,具体得到结果看你算法的设计了,但只要满足DAG图中前后相对关系。
另外观察 1 2 4 3 6 5 7 8 这个序列满足我们所说的有关系的节点指向的在前面,被指向的在后面。如果完全没关系那不一定前后(例如1,2)
对于拓扑排序,如何用代码实现呢?
虽然在上面详细介绍了思路和流程,也很通俗易懂,但是实际上代码的实现还是很需要斟酌的,如何在空间和时间上能够得到较好的平衡且取得较好的效率?
首先要考虑存储,对于节点,是用邻接矩阵还是邻接表存储呢,通常拓扑排序如果使用矩阵存储都是比较稀疏的,比较浪费内存空间,这里还是使用邻接表来存储节点。
另外,如果图中节点是1,2,3,4,5,6这样的有序编号,我们可以直接用数组,但是如果遇到1,2,88,9999类似不连续跨度很大编号节点,也可以考虑用Map存储映射一下位置。
那么我们具体的代码思想为:
①新建node类,包含节点数值和它的指向节点集合(这里直接用List集合)
②初始化一个人node数组,输入/枚举节点之间关系,被指向的节点入度+1!(例如A—>C)那么C的入度+1;
③扫描所有node(这里扫描数组)。将所有入度为0的点加入一个容器栈(队列)中。
④当栈(队列)不空的时候,抛出其中任意一个node(只要入度为零可以随便选择顺序)。将node输出,并且node指向的所有节点入度减1。如果某个点的入度被减为0,那么就将它加入栈(队列)。
⑤重复上述操作,直到栈(队列)为空。
这里主要是利用栈或者队列储存入度只为0的节点,只需要初次扫描表将入度为0的放入栈(队列)中。
因为节点之间是有相关性的,一个节点若想入度为零,那么它的前驱节点点肯定在它前入度为0,拆除关联箭头将自己入度减1,在一个有向无环图中总会有大于等于1个入度为0的节点。
在具体实现上,方式是有多样的,我的这个只是一个简单的演示,效率不一定很高,大家参考一下即可。
具体实现代码为:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
public class tuopu {
static class node
{
int value;
List<Integer> next;
public node(int value) {
this.value=value;
next=new ArrayList<Integer>();
}
public void setnext(List<Integer>list) {
this.next=list;
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
node []nodes=new node[9];//储存节点
int a[]=new int[9];//储存入度
List<Integer>list[]=new ArrayList[10];//临时空间,为了存储指向的集合
for(int i=1;i<9;i++)
{
nodes[i]=new node(i);
list[i]=new ArrayList<Integer>();
}
initmap(nodes,list,a);
//主要流程
//Queue<node>q1=new ArrayDeque<node>();
Stack<node>s1=new Stack<node>();
for(int i=1;i<9;i++)
{
//System.out.print(nodes[i].next.size()+" 55 ");
//System.out.println(a[i]);
if(a[i]==0) {s1.add(nodes[i]);}
}
while(!s1.isEmpty())
{
node n1=s1.pop();//抛出输出
System.out.print(n1.value+" ");
List<Integer>next=n1.next;
for(int i=0;i<next.size();i++)
{
a[next.get(i)]--;//入度减一
if(a[next.get(i)]==0)//如果入度为0
{
s1.add(nodes[next.get(i)]);
}
}
}
}
private static void initmap(node[] nodes, List<Integer>[] list, int[] a) {
list[1].add(3);
nodes[1].setnext(list[1]);
a[3]++;
list[2].add(4);list[2].add(6);
nodes[2].setnext(list[2]);
a[4]++;a[6]++;
list[3].add(5);
nodes[3].setnext(list[3]);
a[5]++;
list[4].add(5);list[4].add(6);
nodes[4].setnext(list[4]);
a[5]++;a[6]++;
list[5].add(7);
nodes[5].setnext(list[5]);
a[7]++;
list[6].add(8);
nodes[6].setnext(list[6]);
a[8]++;
list[7].add(8);
nodes[7].setnext(list[7]);
a[8]++;
}
}输出结果
2 4 6 1 3 5 7 8
至于图的构造,因为没有条件可能效率并不高,算法也可能不太完美,如有优化错误还请大佬指正!
前面说到,拓扑排序需要在有向无环图中才能得到一个拓扑序列,但是如果给定一个有向图,怎么知道它是否可以形成一个拓扑序列呢?
当然是在拓扑排序算法上进行改动,我们在进行拓扑排序会删除所有入度为0的节点,但是如有有环那么删除节点个数就小于所有节点个数,在具体实现上,我们只需要在栈或者队列抛出时候通过一个计数器统计数字即可。
当然这个问题力扣207有原题可以看看自己代码是否能够ac,问题描述:
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
分析上面已经给出,不过在具体实现代码的时候比较灵活,不一定非得创建node类,思路上理的清即可。
实现代码:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int indegree[]=new int[numCourses];
List<Integer> next[]=new ArrayList[numCourses];
for(int i=0;i<numCourses;i++){
next[i]=new ArrayList();
}
for(int i=0;i<prerequisites.length;i++) {
int preid=prerequisites[i][1];
int courseid=prerequisites[i][0];
indegree[courseid]++;//入度加一
next[preid].add(courseid);//next指向
}
Queue<Integer>queue=new ArrayDeque<>();
for(int i=0;i<numCourses;i++) {//加入入度为0的节点
if(indegree[i]==0){
queue.add(i);
}
}
int nodeNum=0;//判断删除节点数量 入度为0删除 如果删除所有那么返回true
while (!queue.isEmpty())
{
nodeNum++;
int nodeId=queue.poll();
for(int i=0;i<next[nodeId].size();i++)
{
int nodeIndex=next[nodeId].get(i);
indegree[nodeIndex]--;
if(indegree[nodeIndex]==0) {
queue.add(nodeIndex);
}
}
}
if(nodeNum==numCourses)
return true;
return false;
}
}好了,到这里拓扑排序内容讲解完毕,如果有帮助还请大家关注、点赞、在看分享一波,谢谢!