输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
提示:
- 1.二叉搜索树是指父亲节点大于左子树中的全部节点,但是小于右子树中的全部节点的树。
- 2.该题我们约定空树不是二叉搜索树
- 3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历
- 4.参考下面的二叉搜索树,示例 1
示例1
输入:[1,3,2]
返回值:true
说明:是上图的后序遍历 ,返回true注意是二叉搜索树,如果是后续遍历的话,那么应该最后一个元素是中间元素 mid,前面的元素可以分为两部分,一部分比 mid 小,另一部分全部比 mid 大。如果破坏这个原则,那么就应该输出No。
采取分而治之的方法,分别递归检查左子树以及右子树:
Java 代码如下:
public boolean VerifySquenceOfBST(int[] sequence) {
if (sequence == null || sequence.length == 0) {
return false;
}
if (sequence.length == 1) {
return true;
}
return verifySection(sequence, 0, sequence.length - 1);
}
private boolean verifySection(int[] sequence, int strat, int end) {
if (strat >= end) {
return true;
}
int mid = sequence[end];
int midIndex = end;
for (int i = strat; i < end; i++) {
if (sequence[i] > mid) {
midIndex = i;
break;
}
}
for (int i = midIndex; i < end; i++) {
if (sequence[i] < mid) {
return false;
}
}
return verifySection(sequence, strat, midIndex - 1) && verifySection(sequence, midIndex, end - 1);
}C++ 代码实现如下:
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if (sequence.size() == 0) {
return false;
}
if (sequence.size() == 1) {
return true;
}
return verifySection(sequence, 0, sequence.size() - 1);
}
bool verifySection(vector<int> sequence, int strat, int end) {
if (strat >= end) {
return true;
}
int mid = sequence[end];
int midIndex = end;
for (int i = strat; i < end; i++) {
if (sequence[i] > mid) {
midIndex = i;
break;
}
}
for (int i = midIndex; i < end; i++) {
if (sequence[i] < mid) {
return false;
}
}
return verifySection(sequence, strat, midIndex - 1) && verifySection(sequence, midIndex, end - 1);
}
};- 时间复杂度:O(n^2^), n 为二叉树节点的个数, 当树为链式时时间复杂度最坏为O(n^2^)
- 空间复杂度:O(n), 当树为链式结构时, 递归深度为 n
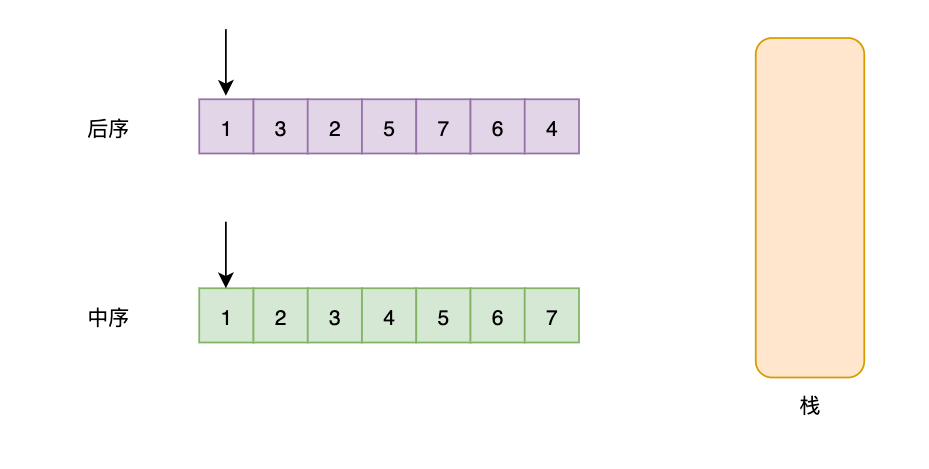
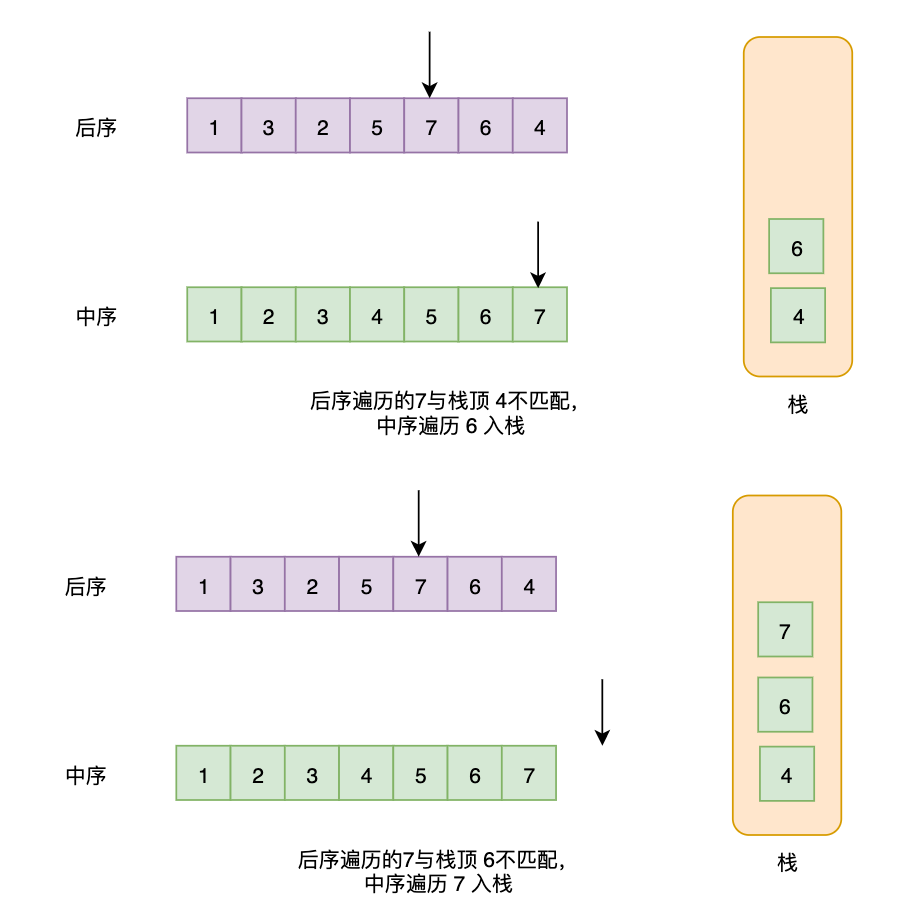
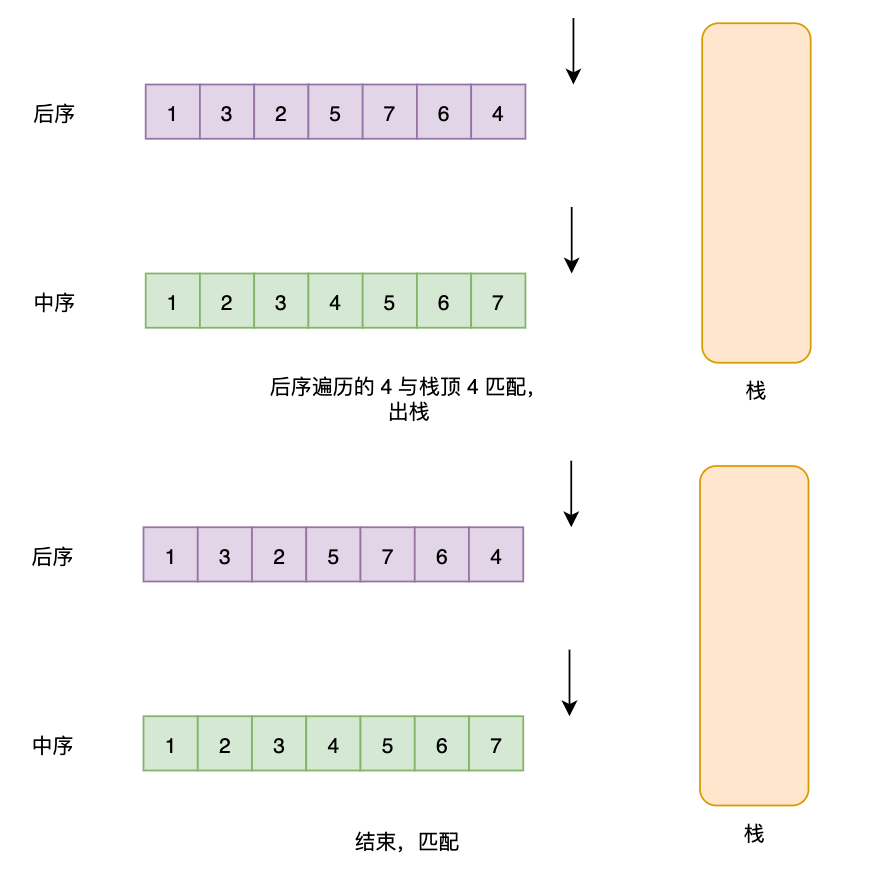
其实这道题还有一种非递归解法,那就是利用后序遍历以及中序遍历进行匹配:
- 首先由于是二叉搜索数,只要我们对输入进行排序,就可以得到中序遍历。
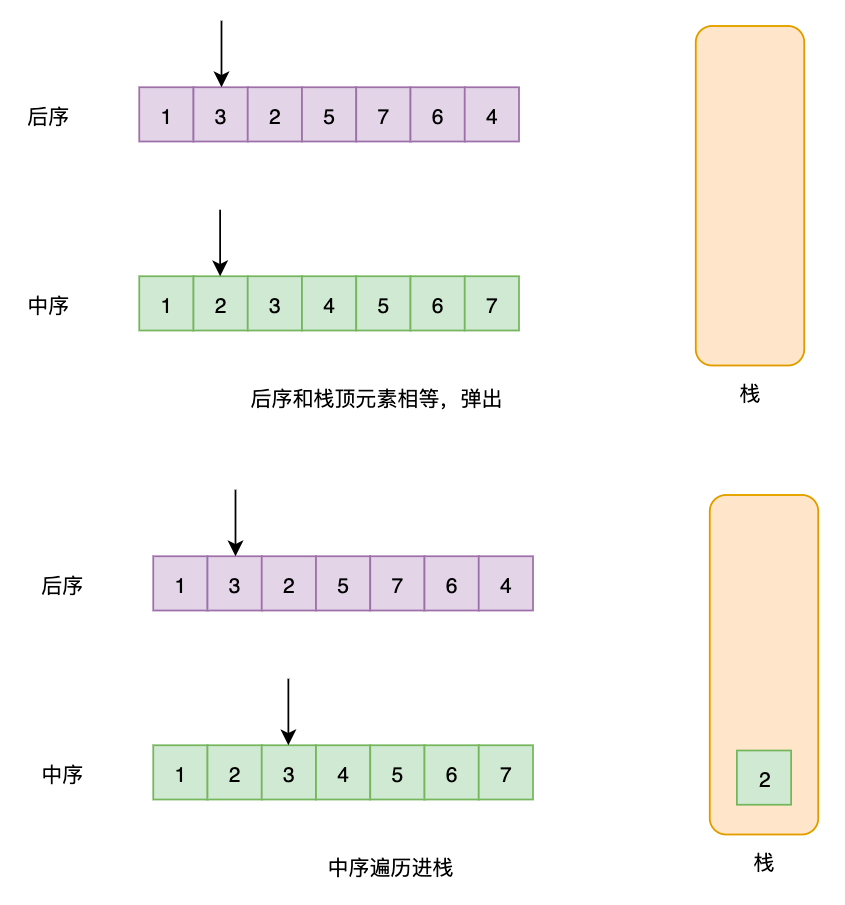
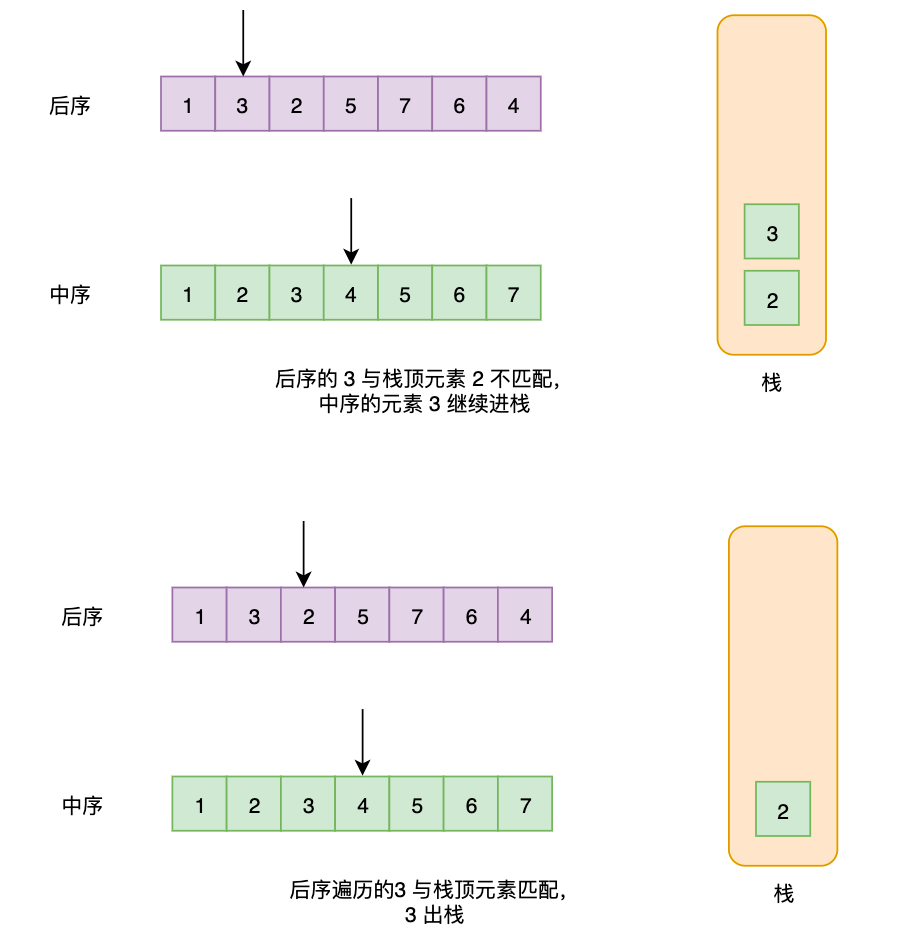
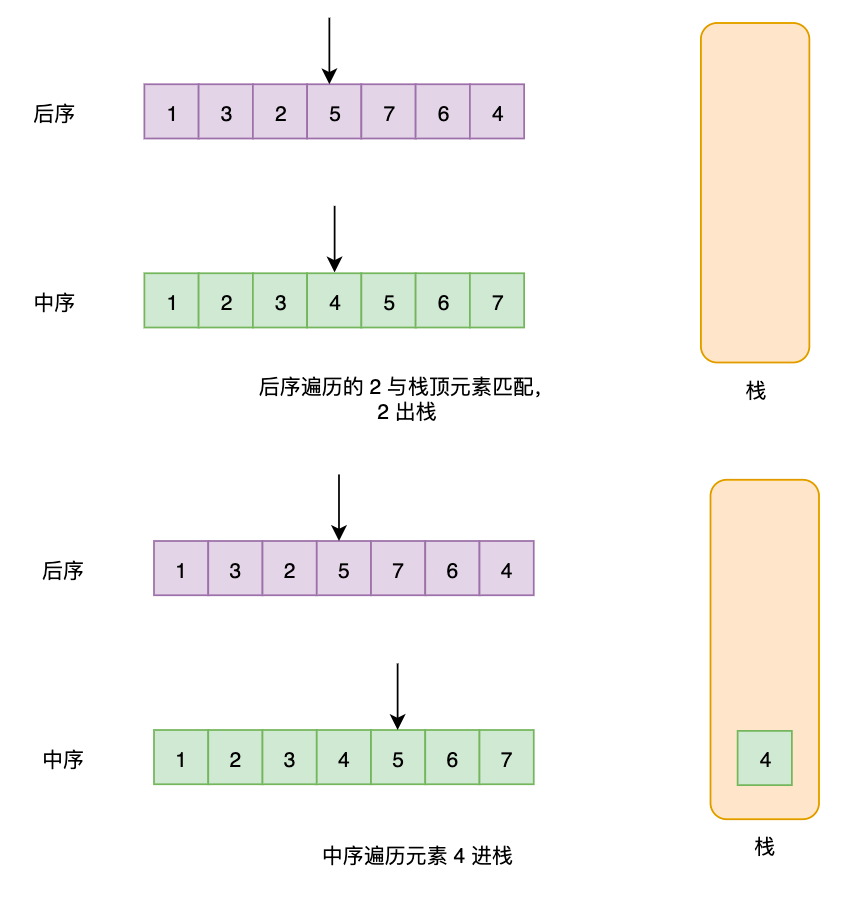
- 将中序遍历的序列逐一进栈,每一次进栈,都对后序遍历的数据进行匹配,匹配就弹出栈
- 如果最终能全部匹配,说明符合。
Java 代码实现如下:
import java.util.Arrays;
import java.util.Stack;
public class Solution {
public boolean VerifySquenceOfBST(int[] sequence) {
if (sequence.length == 0) return false;
int[] inorder = Arrays.copyOf(sequence, sequence.length);
Arrays.sort(inorder);
return isPopOrder(inorder, sequence);
}
boolean isPopOrder(int[] pushV, int[] popV) {
int n = pushV.length;
Stack<Integer> stack = new Stack<>();
int i = 0, j = 0;
while (i < n) {
stack.push(pushV[i]);
while (!stack.empty() && stack.peek() == popV[j]) {
++j;
stack.pop();
}
++i;
}
return j == n;
}
}C++ 代码如下:
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if (sequence.empty()) return false;
vector<int> inorder(sequence);
sort(inorder.begin(), inorder.end());
return isPopOrder(inorder, sequence);
}
bool isPopOrder(vector<int> pushV, vector<int> popV) {
int n = pushV.size();
stack<int> myStack;
int i = 0, j = 0;
while (i < n) {
myStack.push(pushV[i]);
while (!myStack.empty() && myStack.top() == popV[j]) {
j++;
myStack.pop();
}
i++;
}
return j == n;
}
};时间复杂度:O(nlogn), 时间复杂度在于排序,默认排序是O(nlogn)
空间复杂度:O(n), 使用额外的数组以及栈结构