地上有一个 m 行和 n 列的方格。一个机器人从坐标(0,0)的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 k 的格子。 例如,当 k 为 18 时,机器人能够进入方格(35,37),因为 3+5+3+7 = 18。但是,它不能进入方格(35,38),因为 3+5+3+8 = 19。请问该机器人能够达到多少个格子?
示例1
输入
5,10,10
返回值
21
示例3
输入:
10,1,100
返回值:
29
说明:
[0,0],[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8],[0,9],[0,10],[0,11],[0,12],[0,13],[0,14],[0,15],[0,16],[0,17],[0,18],[0,19],[0,20],[0,21],[0,22],[0,23],[0,24],[0,25],[0,26],[0,27],[0,28] 这29种,后面的[0,29],[0,30]以及[0,31]等等是无法到达的。
深度优先搜索算法,也就是 DFS,首先需要初始化数组,注意是 boolean 类型的二元数组。边初始化边计算位数的和,判断如果大于等于阈值的话,就直接置为 true,也就是已经被访问到(但是这一部分计入结果)。
然后遍历每一个元素,只要 i,j 不在合法的索引范围或者是已经被访问过,都会直接返回 false。
否则的话,可访问的数量 +1,并且递归遍历上下左右四个元素,返回最终的可访问的个数。
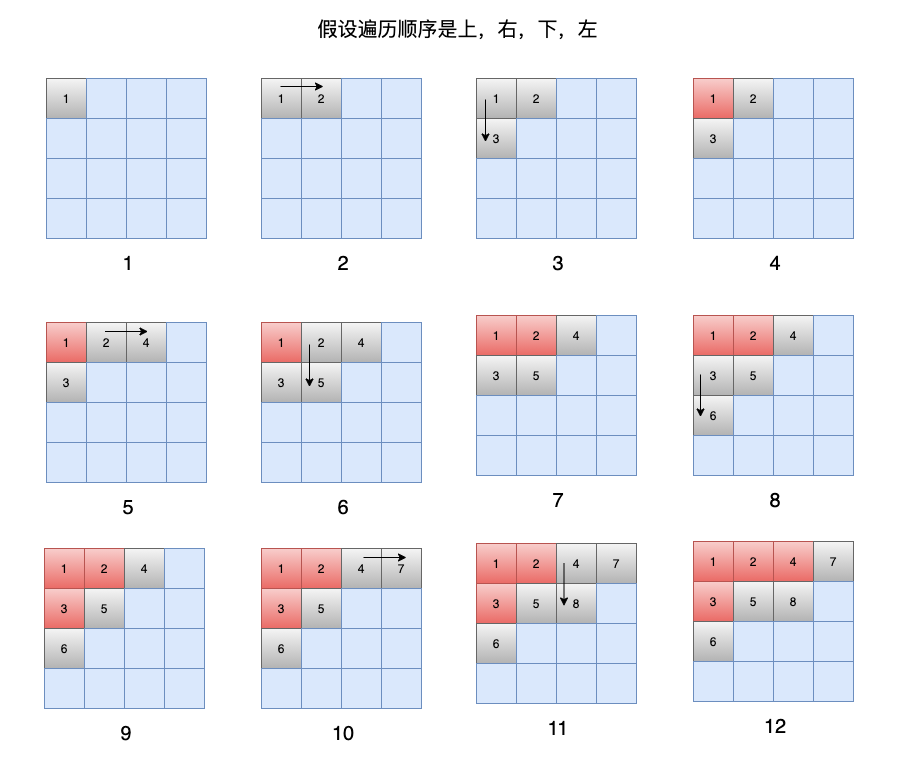
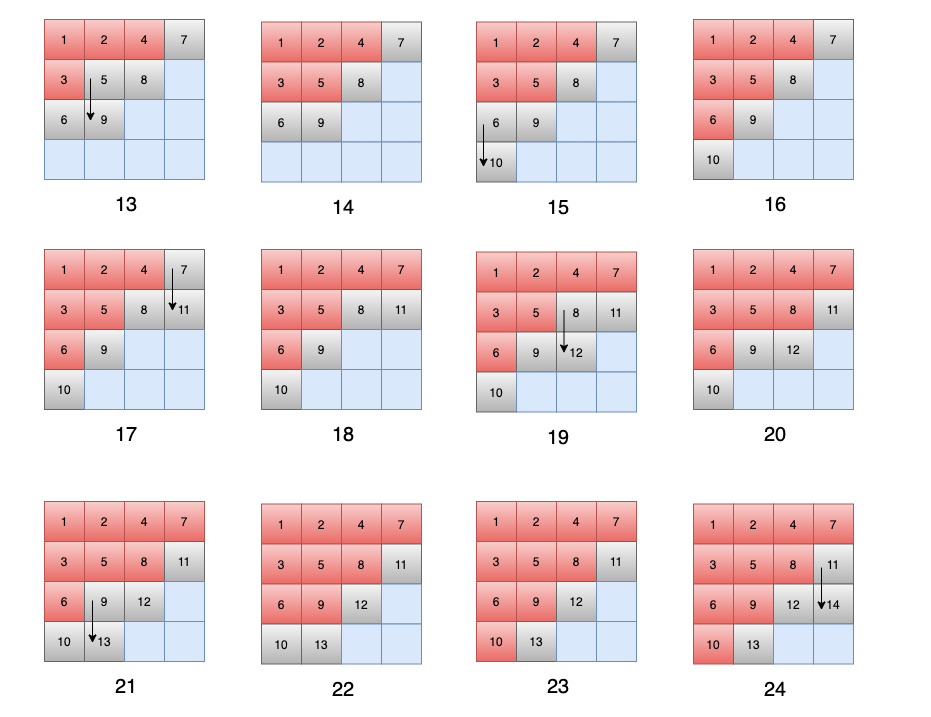
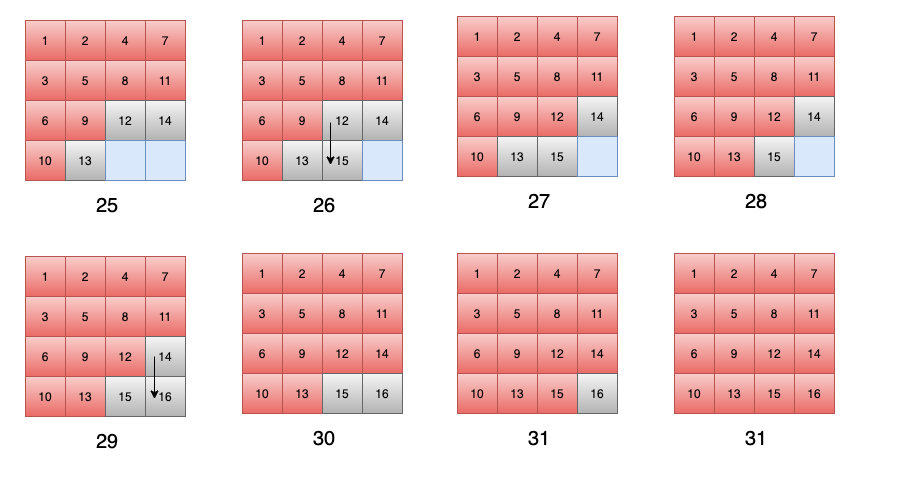
DFS 会优先同一个方向,一直走下去,不撞南墙不回头,直到条件不满足的时候,才会回头。回头之后,每次只会回头一步,往另外一个方向去,同样是一头扎进去。
假设有一个 4 x 4 的方格,从第一个开始遍历,假设遍历顺序是上,右,下,左,那么遍历的顺序应该如此:
public class Solution {
public int movingCount(int threshold, int rows, int cols) {
if (rows > 0 && cols > 0) {
boolean[][] visited = new boolean[rows][cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
// 如果大于阈值,设置已被访问过
visited[i][j] = ((getSum(i) + getSum(j)) > threshold);
}
}
return getNum(visited, 0, 0, 0);
}
return 0;
}
// 获取可以被访问的个数
private int getNum(boolean[][] visited, int i, int j, int count) {
if (i < 0 || j < 0 || i >= visited.length || j >= visited[0].length || visited[i][j]) {
return count;
}
count++;
visited[i][j] = true;
count = getNum(visited, i, j + 1, count);
count = getNum(visited, i, j - 1, count);
count = getNum(visited, i + 1, j, count);
count = getNum(visited, i - 1, j, count);
return count;
}
// 计算位数之和
private int getSum(int num) {
int result = 0;
while (num > 0) {
result = result + num % 10;
num = num / 10;
}
return result;
}
}C++ 解法如下:
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int movingCount(int threshold, int rows, int cols) {
if (rows > 0 && cols > 0) {
vector<vector<bool> > visited(rows, vector<bool>(cols, 0));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
// 如果大于阈值,设置已被访问过
visited[i][j] = ((getSum(i) + getSum(j)) > threshold);
}
}
return getNum(visited, 0, 0, 0);
}
return 0;
}
// 获取可以被访问的个数
int getNum(vector<vector<bool> > &visited, int i, int j, int count) {
if (i < 0 || j < 0 || i >= visited.size() || j >= visited[0].size() || visited[i][j]) {
return count;
}
count++;
visited[i][j] = true;
count = getNum(visited, i, j + 1, count);
count = getNum(visited, i, j - 1, count);
count = getNum(visited, i + 1, j, count);
count = getNum(visited, i - 1, j, count);
return count;
}
// 计算位数之和
int getSum(int num) {
int result = 0;
while (num > 0) {
result = result + num % 10;
num = num / 10;
}
return result;
}
};时间复杂度:最坏的情况是将所有的格子都遍历一遍,O(m*n)。
空间复杂度:借助了额外的空间保存是否被访问过,同样为O(m*n)。
BFS 是什么意思呢?广度优先搜索,也就是没进行一步,优先搜索当前点的各个方向上的点,不急着往下搜索,等搜索完当前点的各个方向的点,再依次把之前搜索的点,取出来,同样先搜索周边的点... 这样直到所有都被搜索完成。
同样有一个 4 x 4 的方格,从第一个开始遍历,假设遍历顺序是上,右,下,左,那么遍历的顺序应该如此:
在上面的过程图示中,我们可以发现,访问是有顺序的,每遍历一个新的方块,都会标一个顺序,然后按照顺序遍历其四个方向。
这也就是广度优先搜索的本质,我们需要一个队列,来保存遍历的顺序,每次都从队列里面取出一个位置,遍历其四周的方块,每次遍历到的点,都会放到队列里面,这样直到队列为空的时候,也就是全部遍历完成。
Java 代码实现如下:
import java.util.LinkedList;
import java.util.Queue;
public class Solution13 {
public int movingCount(int threshold, int rows, int cols) {
boolean[][] visited = new boolean[rows][cols];
int count = 0;
Queue<int[]> queue = new LinkedList<>();
// 把第一个点加到队列里面
queue.add(new int[]{0, 0});
while (queue.size() > 0) {
// 一直取数据,直到队列为空
int[] x = queue.poll();
// 取出来的数据,包含x,y坐标
int i = x[0], j = x[1];
// 如果访问过或者不符合,直接下一个
if (i >= rows || j >= cols || threshold < getSum(i) + getSum(j) || visited[i][j])
continue;
// 置为访问过
visited[i][j] = true;
// 数量增加
count++;
// 右
queue.add(new int[]{i + 1, j});
// 下
queue.add(new int[]{i, j + 1});
}
return count;
}
// 计算位数之和
private int getSum(int num) {
int result = 0;
while (num > 0) {
result = result + num % 10;
num = num / 10;
}
return result;
}
}C++ 实现如下:
class Solution {
public:
int movingCount(int threshold, int rows, int cols) {
vector<vector<bool>> visited(rows, vector<bool>(cols, 0));
int count = 0;
deque<vector<int>> myQueue;
// 把第一个点加到队列里面
myQueue.push_back(vector<int>(2, 0));
while (myQueue.size() > 0) {
// 一直取数据,直到队列为空
vector<int> x = myQueue.front();
myQueue.pop_front();
// 取出来的数据,包含x,y坐标
int i = x[0], j = x[1];
// 如果访问过或者不符合,直接下一个
if (i >= rows || j >= cols || threshold < getSum(i) + getSum(j) || visited[i][j])
continue;
// 置为访问过
visited[i][j] = true;
// 数量增加
count++;
// 右
vector<int> right = vector<int>();
right.push_back(i + 1);
right.push_back(j);
myQueue.push_back(right);
// 下
vector<int> floor = vector<int>();
floor.push_back(i);
floor.push_back(j + 1);
myQueue.push_back(floor);
}
return count;
}
// 计算位数之和
int getSum(int num) {
int result = 0;
while (num > 0) {
result = result + num % 10;
num = num / 10;
}
return result;
}
};时间复杂度:最坏的情况是将所有的格子都遍历一遍,O(m*n)。
空间复杂度:借助了额外的空间保存是否被访问过,同样为O(m*n)。