-
Notifications
You must be signed in to change notification settings - Fork 7
1 8 IEEE 754 與浮點數運算
Jserv 老師曾在你所不知道的 C 語言講座中提到:
呂紹榕 (Louie Lu) 說:
「寫程式三大錯覺:我懂浮點數、我懂 Unicode、我懂時區」
在大學的多個課程中都會提到浮點數運算,但大多時候都只是草草帶過,為了確保我們能夠掌握程式可能出現的特例 (Exception),認真研究浮點數運算是必須要走的一條路。
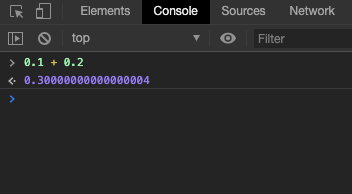
如果說方法/工具是讓人能夠快速解決問題,那規則就是用來統一方法以避免百家爭鳴的狀況發生。 電腦科學家在幾十年來嘗試發展各種在電腦中存放小數的方法,最後則是由 IEEE-754 拿下這一戰的勝利,成為被世人廣泛接受的浮點數方法。 也因為浮點數方法,我們經常在寫程式時碰到奇怪的 Case :
會出現這樣的問題並不是電腦的錯,而是我們不夠了解計算機的行為。
IEEE 二進位浮點數算術標準(IEEE 754)是 20 世紀 80 年代以來最廣泛使用的浮點數運算標準,為許多 CPU 與浮點運算器所採用。這個標準定義了表示浮點數的格式(包括負零-0)與反常值(denormal number),一些特殊數值((無窮(Inf)與非數值(NaN)),以及這些數值的「浮點數運算子」;它也指明了四種數值修約規則和五種例外狀況(包括例外發生的時機與處理方式)。 --wikipedia
IEEE 754 規範了四種浮點數表達方式,分別是:
- 單精確度
- 雙精確度
- 延伸單精確度
- 延伸雙精確度
其中,只有單精確度是必備的,其他皆為選擇性實作。 基本上,上述四種的剖析方法不會有太大的差異,只是更多的位元能夠表達更精確的數值。 因此,本篇文章只會針對單精度浮點數做介紹。
單精度浮點數會佔有 32 bits,而這些空間又會被分配成三個部分,分別是:
- sign(1)
1 表示負數,反之代表正數。
- exponent(8)
8 bits 一共可表示 255 種狀態,為了有效分配指數為正數和負數的情況,IEEE-754 以 127 表示指數為 0 的情況,若我們今天要表示指數為 3 則變成 3 + 127 = 130。
以 2 進制的方式表示 127 :
01111111
- fraction(23)
存放小數資料。
看完上面的介紹不一定能學會浮點數運算,為了避免讀者沒看懂,讓我們來實際操作一次看看:
以 8.5 為例,若要將它以 IEEE 754 規範的形式表示的話必須先做正規化,也就是將 8.5 拆成 8 + 0.5 再轉為 2 進制:
8.5 = 2³ + 1/2¹
2³ + 1/2¹ = 1000.1
最後再讓整數部分僅剩個位數 1 : 1.0001 x 2³。
前面已經介紹過單精度浮點數是如何分配 32 個位置,所以我們直接來看要怎麼把 1.0001 x 2³ 存放到 32 bits 的記憶體中吧!
- sign 因為 8.5 是正數,所以 sign bit 存放 0。
- exponent
在剛剛,我們得到了 1.0001 x 2³ 的結果,而 exponent 就是 3。
你認為這樣就結束了嗎?
不!剛剛有提到這邊以 +127 作為 0,所以要表示 3 我們必須將 127 + 3。因此,我們在這邊會在 8 bits 中存放:
10000010 (130) - fraction
在處理完 sign 和 exponent 的部分後,我們只要將剩餘的小數部分處理就大功告成啦!
fraction 一共被分配到 23 個 bit,以 8.5 為例,我們僅會存放
.0001,所以在記憶體中看起來會像是:00010000000000000000000
將上面三個部分都處理完成後,在 32-bit 的記憶體模型上看起來就會是這樣:
0 10000010 00010000000000000000000
此外,IEEE-754 Floating Point Converter 是一個很棒的小工具,我們可以利用它進行浮點數轉換以及查看記憶體模型。
關於浮點數的命名由來,我們可以透過維基百科查找其定義:
在計算機科學中,浮點(英語:floating point,縮寫為FP)是一種對於實數的近似值數值表現法,由一個有效數字(即尾數)加上冪數來表示,通常是乘以某個基數的整數次指數得到。以這種表示法表示的數值,稱為浮點數(floating-point number)。利用浮點進行運算,稱為浮點計算,這種運算通常伴隨著因為無法精確表示而進行的近似或捨入。 -- wikipedia
因為記憶體有限,若要完整存放多位數的小數(定點數)將會佔有非常大的記憶體空間,浮點數算是犧牲準確度換來空間使用率的折衷作法。
如何定義一個人很會寫程式?除了常見的設計思維、物件導向...,在開發時更會使用相關工具以提升效率或是進行驗證 (Git, GDB...)。不過,上述這些東西都不能代表你很會寫程式。真正的程式高手是能熟知各種情況下的特例並做出良好的應對處理的,像是: 並不是每個程式開發者都知道程式語言中的小數問題是浮點數規範造成的,更不用說知道如何應對的人更是寥寥可數。
由此可知,筆者也不太會寫程式。不過筆者認為: 無知並不可怕,真正可怕的是無知而不自知的人。 這也是為何筆者想藉由撰寫文章探討各種議題的主要原因。
在 IEEE-754 中,為了保留正無窮 (exponent = 255) 和負無窮 (exponent = 0),因此,最大及最小的整數的 exponent 分別是 254 以及 1 :
從上面的表格中,有可以看到幾個浮點數的特例,分別是:
-
+-0 當 exponent 與 fraction 皆為 0,其值為 +-0。
-
+-∞ 當 exponent 為 255 且 fraction 為 0,其值為無窮大。
-
NaN 當 exponent 為 255 且 fraction 不為 0,表示 Not a number。此外,根據 IEEE 754 2008 年版本可以得知 NaN 被歸類為兩種:
- Quiet NaN
- Signal NaN
X111 1111 1AXX XXXX XXXX XXXX XXXX XXXX我們可以透過從低位數來的第 23 個位元(也就是上面 A 所在的位置) 判斷 NaN 的種類,如果在 A 的位置為 1,則為 Quiet NaN,否則為 Signal NaN。 兩者的差別我們也可以從 Intel manual 中得知:
SNaNs are typically used to trap or invoke an exception handler. They must be inserted by software; that is, the processor never generates an SNaN as a result of a floating-point operation.
Signal NaN 不會由處理器運算產生且對其做運算會對電腦發出訊號進入異常處理。相反的,Quiet NaN 經由處理器運算後並不會造成程式終止。關於 NaN,可以在 What is the difference between quiet NaN and signaling NaN? 這個問答串中找到網友對兩種 NaN 設計的實驗:
#include <cassert>
#include <cfenv>
#include <cmath> // isnan
#include <iostream>
#include <limits> // std::numeric_limits
#include <unistd.h>
#pragma STDC FENV_ACCESS ON
int main() {
float snan = std::numeric_limits<float>::signaling_NaN();
float qnan = std::numeric_limits<float>::quiet_NaN();
float f;
// No exceptions.
assert(std::fetestexcept(FE_ALL_EXCEPT) == 0);
// Still no exceptions because qNaN.
f = qnan + 1.0f;
assert(std::isnan(f));
if (std::fetestexcept(FE_ALL_EXCEPT) == FE_INVALID)
std::cout << "FE_ALL_EXCEPT qnan + 1.0f" << std::endl;
// Now we can get an exception because sNaN, but signals are disabled.
f = snan + 1.0f;
assert(std::isnan(f));
if (std::fetestexcept(FE_ALL_EXCEPT) == FE_INVALID)
std::cout << "FE_ALL_EXCEPT snan + 1.0f" << std::endl;
feclearexcept(FE_ALL_EXCEPT);
// And now we enable signals and blow up with SIGFPE! >:-)
feenableexcept(FE_INVALID);
f = qnan + 1.0f;
std::cout << "feenableexcept qnan + 1.0f" << std::endl;
f = snan + 1.0f;
編譯並執行上面的程式碼便可以取得 exit status:
g++ -ggdb3 -O0 -Wall -Wextra -pthread -std=c++11 -pedantic-errors -o blow_up.out blow_up.cpp -lm -lrt
./blow_up.out
echo $?
- 非正規數
當 exponent 為 0 且 fraction 不為 0 時,該浮點數為非正規數。用數線來看的話,大概長這樣:
-∞ ~ (sign = 1)最大正規數 ~ -1 ~ (sign = 1)最小正規數 ~ (sign = 1)最大的非正規數 ~ (sign = 1)最小的非正規數 ~ -0/+0 ~ (sign = 0)最小的非正規數 ~ (sign = 0)最大的非正規數 ~ (sign = 0)最小正規數 ~ (sign = 0)最大正規數 ~ +∞除了規約浮點數,IEEE754-1985標準採用非規約浮點數,用來解決填補絕對值意義下最小規格數與零的距離。(舉例說,正數下,最大的非規格數等於最小的規格數。而一個浮點數編碼中,如果exponent=0,且尾數部分不為零,那麼就按照非規約浮點數來解析)非規約浮點數源於70年代末IEEE浮點數標準化專業技術委員會醞釀浮點數二進位標準時,Intel公司對漸進式下溢位(gradual underflow)的力薦。當時十分流行的DEC VAX機的浮點數表示採用了突然式下溢位(abrupt underflow)。如果沒有漸進式下溢位,那麼0與絕對值最小的浮點數之間的距離(gap)將大於相鄰的小浮點數之間的距離。 -- wikipedia
為了節省空間,每次進行浮點數運算都會產生一定的誤差值,為了解決問題,Kahan 教授提出了 Kahan Summation 對每次的浮點運算做補償以修正這個問題。
在學習 Kahan Summation 之前,必須先了解 Precision (準確度) 和 Accuracy (精密度) 的差別。
以 3.14159 為例,如果我們只以小數點後 6 位為標準,我們可以用四個數字詮釋準確度與精密度:
- Accurate && Precise 3.14159
- Accurate && Inprecise 3.14
- Inaccurate && Precise 3.14128
- Inaccurate && Inprecise 3.22
使用更多位元表達浮點數是為了取得更高的準確度,而 Kahan Summation 則是為了修正浮點數運算的精密度誤差。
function KahanSum(input)
var sum = 0.0 // Prepare the accumulator.
var c = 0.0 // A running compensation for lost low-order bits.
for i = 1 to input.length do // The array input has elements indexed input[1] to input[input.length].
var y = input[i] - c // c is zero the first time around.
var t = sum + y // Alas, sum is big, y small, so low-order digits of y are lost.
c = (t - sum) - y // (t - sum) cancels the high-order part of y; subtracting y recovers negative (low part of y)
sum = t // Algebraically, c should always be zero. Beware overly-aggressive optimizing compilers!
next i // Next time around, the lost low part will be added to y in a fresh attempt.
return sum
當有效位數有限且有大數與一個小數做運算時,就會因為能表達的有效位數不足導致後面的數字遺失,例如:
10000.0 + 3.14159 = 10003.14159
假設有效位數為 6,運算結果就會變成:
10000.0 + 3.14159 = 10003.1
Kahan Summation 的作法就是算出這些遺失的值,等到下一輪運算再將他補嘗到新的輸入當中:
/* 求出誤差值 */
c = (10003.1 - 10000.0) - 3.14159 //-0.04159
/* 補償 */
y = 3.00001 - (-0.04159) //假設下一輪運算的輸入是 3.00001
透過 Kahan Summation,在新一輪的輸入與上一輪產生的誤差值等位時,就可以完全的補償浮點數運算造成的精密度下降。實際上,Kahan Summation 只能盡可能的補償誤差,如果新一輪的輸入與上一輪產生的誤差值的大小差距過大,補償的效果就不會這麼的顯著。