Yet Another Text Book¶

import matplotlib
+import matplotlib.pyplot as plt
+import numpy as np
+%matplotlib inline
+plt.style.use('seaborn-whitegrid')
+
+font = {'family' : 'Times',
+ 'weight' : 'bold',
+ 'size' : 12}
+
+matplotlib.rc('font', **font)
+
+
+# Aux functions
+
+def plot_grid(Xs, Ys, axs=None):
+ ''' Aux function to plot a grid'''
+ t = np.arange(Xs.size) # define progression of int for indexing colormap
+ if axs:
+ axs.plot(0, 0, marker='*', color='r', linestyle='none') #plot origin
+ axs.scatter(Xs,Ys, c=t, cmap='jet', marker='.') # scatter x vs y
+ axs.axis('scaled') # axis scaled
+ else:
+ plt.plot(0, 0, marker='*', color='r', linestyle='none') #plot origin
+ plt.scatter(Xs,Ys, c=t, cmap='jet', marker='.') # scatter x vs y
+ plt.axis('scaled') # axis scaled
+
+def linear_map(A, Xs, Ys):
+ '''Map src points with A'''
+ # [NxN,NxN] -> NxNx2 # add 3-rd axis, like adding another layer
+ src = np.stack((Xs,Ys), axis=Xs.ndim)
+ # flatten first two dimension
+ # (NN)x2
+ src_r = src.reshape(-1,src.shape[-1]) #ask reshape to keep last dimension and adjust the rest
+ # 2x2 @ 2x(NN)
+ dst = A @ src_r.T # 2xNN
+ #(NN)x2 and then reshape as NxNx2
+ dst = (dst.T).reshape(src.shape)
+ # Access X and Y
+ return dst[...,0], dst[...,1]
+
+
+def plot_points(ax, Xs, Ys, col='red', unit=None, linestyle='solid'):
+ '''Plots points'''
+ ax.set_aspect('equal')
+ ax.grid(True, which='both')
+ ax.axhline(y=0, color='gray', linestyle="--")
+ ax.axvline(x=0, color='gray', linestyle="--")
+ ax.plot(Xs, Ys, color=col)
+ if unit is None:
+ plotVectors(ax, [[0,1],[1,0]], ['gray']*2, alpha=1, linestyle=linestyle)
+ else:
+ plotVectors(ax, unit, [col]*2, alpha=1, linestyle=linestyle)
+
+def plotVectors(ax, vecs, cols, alpha=1, linestyle='solid'):
+ '''Plot set of vectors.'''
+ for i in range(len(vecs)):
+ x = np.concatenate([[0,0], vecs[i]])
+ ax.quiver([x[0]],
+ [x[1]],
+ [x[2]],
+ [x[3]],
+ angles='xy', scale_units='xy', scale=1, color=cols[i],
+ alpha=alpha, linestyle=linestyle, linewidth=2)
+/var/folders/rt/lg7n4lt1489270pz_18qn1_c0000gp/T/ipykernel_18217/1496334134.py:5: MatplotlibDeprecationWarning: The seaborn styles shipped by Matplotlib are deprecated since 3.6, as they no longer correspond to the styles shipped by seaborn. However, they will remain available as 'seaborn-v0_8-<style>'. Alternatively, directly use the seaborn API instead.
+ plt.style.use('seaborn-whitegrid')
+
+import matplotlib
+import matplotlib.pyplot as plt
+import numpy as np
+%matplotlib inline
+plt.style.use('seaborn-whitegrid')
+
+font = {'family' : 'Times',
+ 'weight' : 'bold',
+ 'size' : 12}
+
+matplotlib.rc('font', **font)
+
+
+# Aux functions
+
+def plot_grid(Xs, Ys, axs=None):
+ ''' Aux function to plot a grid'''
+ t = np.arange(Xs.size) # define progression of int for indexing colormap
+ if axs:
+ axs.plot(0, 0, marker='*', color='r', linestyle='none') #plot origin
+ axs.scatter(Xs,Ys, c=t, cmap='jet', marker='.') # scatter x vs y
+ axs.axis('scaled') # axis scaled
+ else:
+ plt.plot(0, 0, marker='*', color='r', linestyle='none') #plot origin
+ plt.scatter(Xs,Ys, c=t, cmap='jet', marker='.') # scatter x vs y
+ plt.axis('scaled') # axis scaled
+
+def linear_map(A, Xs, Ys):
+ '''Map src points with A'''
+ # [NxN,NxN] -> NxNx2 # add 3-rd axis, like adding another layer
+ src = np.stack((Xs,Ys), axis=Xs.ndim)
+ # flatten first two dimension
+ # (NN)x2
+ src_r = src.reshape(-1,src.shape[-1]) #ask reshape to keep last dimension and adjust the rest
+ # 2x2 @ 2x(NN)
+ dst = A @ src_r.T # 2xNN
+ #(NN)x2 and then reshape as NxNx2
+ dst = (dst.T).reshape(src.shape)
+ # Access X and Y
+ return dst[...,0], dst[...,1]
+
+
+def plot_points(ax, Xs, Ys, col='red', unit=None, linestyle='solid'):
+ '''Plots points'''
+ ax.set_aspect('equal')
+ ax.grid(True, which='both')
+ ax.axhline(y=0, color='gray', linestyle="--")
+ ax.axvline(x=0, color='gray', linestyle="--")
+ ax.plot(Xs, Ys, color=col)
+ if unit is None:
+ plotVectors(ax, [[0,1],[1,0]], ['gray']*2, alpha=1, linestyle=linestyle)
+ else:
+ plotVectors(ax, unit, [col]*2, alpha=1, linestyle=linestyle)
+
+def plotVectors(ax, vecs, cols, alpha=1, linestyle='solid'):
+ '''Plot set of vectors.'''
+ for i in range(len(vecs)):
+ x = np.concatenate([[0,0], vecs[i]])
+ ax.quiver([x[0]],
+ [x[1]],
+ [x[2]],
+ [x[3]],
+ angles='xy', scale_units='xy', scale=1, color=cols[i],
+ alpha=alpha, linestyle=linestyle, linewidth=2)
+/var/folders/rt/lg7n4lt1489270pz_18qn1_c0000gp/T/ipykernel_18217/1496334134.py:5: MatplotlibDeprecationWarning: The seaborn styles shipped by Matplotlib are deprecated since 3.6, as they no longer correspond to the styles shipped by seaborn. However, they will remain available as 'seaborn-v0_8-<style>'. Alternatively, directly use the seaborn API instead.
+ plt.style.use('seaborn-whitegrid')
+
+
| Topic | +Hours | +
|---|---|
| Intro, Math Recap | +- | +
| Unsupervised Learning | +|
| Dimensionality Reduction (PCA, Eigenvectors, SVD) | +- | +
| Clustering (kmeans, GMM) | +- | +
| Supervised Learning, Non-parametric | +|
| Nearest Neighbours | +- | +
| Decision trees | +- | +
| Supervised Learning, Parametric | +|
| Linear Regression with Least Squares | +- | +
| Polynomial regression, under/overfitting | +- | +
| - | +|
| $\star$ Perceptron, Logistic Regression (LR) | +- | +
| Deep Learning | +|
| $\star$ Perceptron, Logistic Regression (LR) from LR to Neural Nets | +- | +
| Total | +60 | +
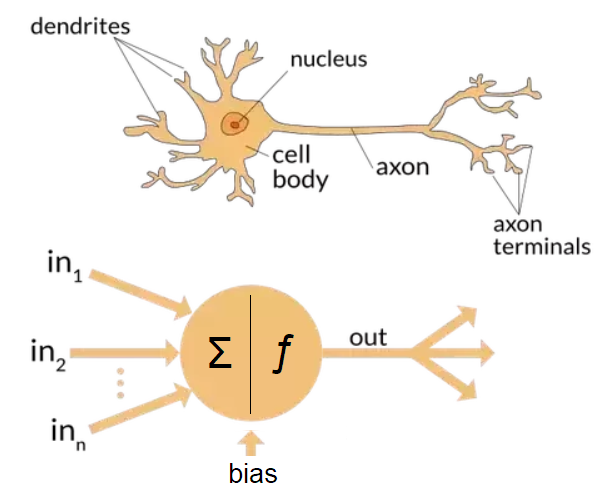
“Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms” published in 1962
+ +
$\mbf{x}_i \in \mathbb{R}^d$ and $y \in \{0,1\}$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \sigma\left( \bmf{\theta}^T\mbf{x} \right)$$where:
+$$ \sigma(z)= \begin{cases} +1, & \mbox{if } z\ge0 \\ +0, & \mbox{if } z<0\end{cases}$$
+{{import numpy as np;import matplotlib.pyplot as plt;x = np.arange(-20.0, 20.0, 0.1);y = np.maximum(np.sign(x),0);_=plt.plot(x,y);}}
A few observations:
+
A few observations:
+
A few observations:
+






the angle is less than 90 deg, change $\theta \leftarrow \theta-\gamma\mbf{x}$the angle is more than 90 deg, change $\theta \leftarrow \theta+\gamma\mbf{x}$
the angle is less than 90 deg, change $\theta \leftarrow \theta-\gamma\mbf{x}$the angle is more than 90 deg, change $\theta \leftarrow \theta+\gamma\mbf{x}$
the angle is less than 90 deg, change $\theta \leftarrow \theta-\gamma\mbf{x}$the angle is more than 90 deg, change $\theta \leftarrow \theta+\gamma\mbf{x}$
$\theta$ is a linear combination of training samples $\{\mbf{x}_i,y_i\}$
+ +Given a linearly separable training set, the Perceptron will find a generic solution of the infinite many that classifies correctly all the points (separate all the points neatly).
+margin between points). Small margins require more time to converge.
from sklearn.linear_model import Perceptron
+from sklearn.preprocessing import PolynomialFeatures
+import numpy as np
+
+lift_features = True
+
+X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
+y = X[:, 0] ^ X[:, 1]
+
+if lift_features:
+ print('X before=',X, sep='\n')
+ X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
+ print('X before=',X,y.T, sep='\n')
+clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
+ shuffle=False).fit(X, y)
+clf.predict(X)
+clf.score(X, y)
+X before= +[[0 0] + [0 1] + [1 0] + [1 1]] +X before= +[[1 0 0 0] + [1 0 1 0] + [1 1 0 0] + [1 1 1 1]] +[0 1 1 0] ++
1.0+
from sklearn.datasets import make_classification
+
+X, y = make_classification(
+ n_features=2, n_redundant=0, n_informative=2,
+ n_clusters_per_class=1, random_state=0, class_sep=2.8)
+plt.scatter(*X.T,c=y,cmap='jet');
+from sklearn.datasets import make_classification
+from matplotlib import cm
+from celluloid import Camera
+from IPython.display import HTML
+
+def get_support(minx, maxx):
+ support = np.linspace(minx, maxx, 100)
+ xx, yy = np.meshgrid(support, support)
+ points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+ points = add_ones(points)
+ return points, xx, yy
+
+def plot_separating_plane(w, minx, maxx, points, xx, yy):
+ dist = perceptron(w, points.T)
+ dist = dist.reshape(xx.shape)
+ plt.contourf(xx, yy, dist, cmap=cm.get_cmap("RdBu"))
+ plt.plot(0, 0, 'rx')
+ plt.axis('scaled')
+ plt.xlim(minx, maxx)
+
+
+def perceptron(w, xi):
+ return np.maximum(np.sign(np.dot(w, xi)), 0)
+
+
+def add_ones(X):
+ bias = np.ones((X.shape[0], 1))
+ X = np.hstack((X, bias))
+ return X
+
+def done(w, X):
+ return np.all(y == perceptron(w, X.T))
+
+
+def plot_classification(theta_curr, minx, maxx, support, xx, yy, X):
+ plot_separating_plane(theta_curr, minx, maxx, support, xx, yy)
+ plt.scatter(X[:, 0], X[:, 1], s=80,c=y,
+ facecolors="none",
+ zorder=10,
+ edgecolors="k",
+ cmap=cm.get_cmap("RdBu"))
+
+### CAMERA ##########
+fig = plt.figure()
+camera = Camera(fig)
+
+################## DATA #####################
+#X, y = make_classification(
+# n_features=2, n_redundant=0, n_informative=2,
+# n_clusters_per_class=1,
+# random_state=0, class_sep=2.8)
+minx, maxx = X.min(), X.max()
+support, xx, yy = get_support(minx, maxx)
+X = add_ones(X)
+############### PARAMS ########################
+theta_curr = np.array([[-1, -2, 0]])
+gamma = 1e-2
+i = 0
+text_kwargs = dict(ha='center', va='center', fontsize=10, color='C1')
+################################################
+plot_separating_plane(theta_curr, minx, maxx, support, xx, yy)
+exit = False
+# while not all are classified
+while not done(theta_curr,X) and i < 300:
+ # for all points
+ for xi, yi in zip(X, y):
+ prediction = perceptron(theta_curr, xi)
+ # if prediction is wrong, update
+ if prediction != yi:
+ diff = yi - perceptron(theta_curr, xi)
+ theta_curr = theta_curr + gamma * diff * xi
+ plot_classification(theta_curr, minx, maxx, support, xx, yy, X)
+ i += 1
+ plt.text(-4, 4.5, str(i), **text_kwargs)
+ camera.snap()
+# write 20 frames with the last result for memory
+for i in range(20):
+ plot_classification(theta_curr, minx, maxx, support, xx, yy, X)
+ camera.snap()
+animation = camera.animate()
+HTML(animation.to_html5_video())
+
where:
+$$ \sigma(z)= \frac{1}{1+\exp^{-z}} \quad \text{sigmoid or logistic function}$$
We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\bmf{\theta}) = f_{\boldsymbol{\theta}}\\ +p(y=0| \mbf{x};\bmf{\theta}) = ?\\ +\end{cases} $$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \sigma\left( \bmf{\theta}^T\mbf{x} \right)$$
where:
+$$ \sigma(z)= \frac{1}{1+\exp^{-z}} \quad \text{sigmoid or logistic function}$$ +We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\bmf{\theta}) = f_{\boldsymbol{\theta}}\\ +p(y=0| \mbf{x};\bmf{\theta}) = 1- f_{\boldsymbol{\theta}}\ +\end{cases} $$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \sigma\left( \bmf{\theta}^T\mbf{x} \right)$$
where:
+$$ \sigma(z)= \frac{1}{1+\exp^{-z}} \quad \text{sigmoid or logistic function}$$$$\lim_{z\mapsto \infty}\sigma(z)=1$$$$\lim_{z\mapsto -\infty}\sigma(z)=0$$ +We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\bmf{\theta}) = f_{\boldsymbol{\theta}}\\ +p(y=0| \mbf{x};\bmf{\theta}) = 1- f_{\boldsymbol{\theta}}\ +\end{cases} $$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \frac{1}{1+\exp^{-\bmf{\theta}^T\mbf{x}}}$$
import numpy as np;
+import matplotlib.pyplot as plt;
+x = np.arange(-20.0, 20.0, 0.1);
+ws = np.array([0, 0.01,0.1,0.5,1,2,10,30])
+for w in ws:
+ y = 1/(1+np.exp(-w*x));
+ plt.plot(x,y);
+plt.legend(ws);
+import numpy as np;
+import matplotlib.pyplot as plt;
+x = np.arange(-20.0, 20.0, 0.1);
+ws = np.array([0, 0.01,0.1,0.5,1,2,10,30])*-1
+for w in ws:
+ y = 1/(1+np.exp(-w*x));
+ plt.plot(x,y);
+plt.legend(ws);
+Points on the decision boundary: $~~~\bmf{\theta}^T\mbf{x}=0$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \frac{1}{1+\exp^{-\bmf{\theta}^T\mbf{x}}} = \frac{1}{1+\exp^{0}} = \frac{1}{1+1}=\frac{1}{2}$$import numpy as np;import matplotlib.pyplot as plt;x = np.arange(-20.0, 20.0, 0.1);y = 1/(1+np.exp(-x));plt.plot(x,y);plt.plot(x,1-y);_=plt.legend(['p(y=1|x)','p(y=0|x)'])
+In general the threshold is 0.5 to map it to a predicted class.
+$$\frac{1}{1+\exp^{-\bmf{\theta}^T\mbf{x}}} > 0.5$$import numpy as np;import matplotlib.pyplot as plt;x = np.arange(-20.0, 20.0, 0.1);y = 1/(1+np.exp(-x));plt.plot(x,y);plt.plot(x,1-y);_=plt.legend(['p(y=1|x)','p(y=0|x)'])
+We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\bmf{\theta}) = f_{\boldsymbol{\theta}}\\ +p(y=0| \mbf{x};\bmf{\theta}) = 1- f_{\boldsymbol{\theta}}\\ +\end{cases} $$For a single point, the if else above based on the $y$ can be written compactly as:
Which discrete distribution does the equation above resemble?
+ +| Data Type $y$ | +Expo. Family | +Name/ML Topic | +
|---|---|---|
| $\mathbb{R}$ | +Gaussian LaPlace |
+Regression | +
| $\{0,1\}$ | +Bernoulli | +Binary Classification | +
| $\{1,K\}$ | +Categorical | +Multi-class Classification | +
| $\mathbb{N}_{+}$ | +Poisson | +Poisson Regression (Counts) | +
| Categorical | +Dirichlet | +More advanced Topics | +
Property of GLM
+| Data Type $y$ | +Expo. Family | +Name | +
|---|---|---|
| $\mathbb{R}$ | +Gaussian LaPlace |
+Regression | +
| $\{0,1\}$ | +Bernoulli | +Binary Classification | +
| $\{1,K\}$ | +Categorical | +Multi-class Classification | +
| $\mathbb{N}_{+}$ | +Poisson | +Poisson Regression | +
| Categorical | +Dirichlet | +More advanced Topics | +
| Data Type $y$ | +Expo. Family | +Name | +
|---|---|---|
| $\mathbb{R}$ | +Gaussian LaPlace |
+Regression | +
Generation process: $$ y = \mathcal{N}(\bmf{\theta}^T\mbf{x};\sigma^2)~~ \text{same as }~~ y = \theta^T\mbf{x} + \epsilon~~\text{with}~~\epsilon \sim \mathcal{N}(0;\sigma^2)$$
+ +Generation process: $$ y = \mathcal{N}(\bmf{\theta}^T\mbf{x};\sigma^2)~~ \text{same as }~~ y = \theta^T\mbf{x} + \epsilon~~\text{with}~~\epsilon \sim \mathcal{N}(0;\sigma^2)$$
+
Generation process: $$ y = \mathcal{N}(\bmf{\theta}^T\mbf{x};\sigma^2)~~ \text{same as }~~ y = \theta^T\mbf{x} + \epsilon~~\text{with}~~\epsilon \sim \mathcal{N}(0;\sigma^2)$$
+
Generation process: $$ y = \mathcal{N}(\bmf{\theta}^T\mbf{x};\sigma^2)~~ \text{same as }~~ y = \theta^T\mbf{x} + \epsilon~~\text{with}~~\epsilon \sim \mathcal{N}(0;\sigma^2)$$
+

We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\bmf{\theta}) = f_{\boldsymbol{\theta}}\\ +p(y=0| \mbf{x};\bmf{\theta}) = 1- f_{\boldsymbol{\theta}}\ +\end{cases} $$For multiple training points, using I.I.D. assumptions:
+$$ +\begin{aligned} +L(\theta;\mbf{X};\mbf{y}) &=p(\vec{y} \mid X ; \theta) =\\ +L(\theta;\mbf{X};\mbf{y}) &=p(\vec{y} \mid {\mbf{x}_1,\ldots,\mbf{x}_n} ; \theta)= [IID] \\ +&=\prod_{i=1}^{n} p\left(y^{(i)} \mid x^{(i)} ; \theta\right) \\ +&=\prod_{i=1}^{n}\left(f_{\boldsymbol{\theta}}\left(x^{(i)}\right)\right)^{y^{(i)}}\left(1-f_{\boldsymbol{\theta}}\left(x^{(i)}\right)\right)^{1-y^{(i)}} +\end{aligned} +$$ +We get the Log-loss that we have seen in the lecture on evaluating the models!
+
+$$
+\begin{aligned}
+\ell(\theta) &=\log L(\theta) \\
+&=\sum_{i=1}^{n} y^{(i)} \log f\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-f\left(x^{(i)}\right)\right)
+\end{aligned}
+$$
We get the Log-loss that we have seen in the lecture on evaluating the models!
+$$ +\begin{aligned} +&\nabla_{\theta}\log L(\theta)= \\ +&=\nabla_{\theta}\sum_{i=1}^{n} y^{(i)} \log f_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-f_{\theta}\left(x^{(i)}\right)\right) +\end{aligned} +$$but before let's compute the gradient of the logistic function.
+ +We get the Log-loss that we have seen in the lecture on evaluating the models!
+$$ +\begin{aligned} +&\nabla_{\theta}\log L(\theta)= \\ +&=\nabla_{\theta}\sum_{i=1}^{n} y^{(i)} \log f_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-f_{\theta}\left(x^{(i)}\right)\right) +\end{aligned} +$$ +We get the Log-loss that we have seen in the lecture on evaluating the models!
+$$ +\begin{aligned} +&\nabla_{\theta}\log L(\theta)= \\ +&=\nabla_{\theta}\sum_{i=1}^{n} y^{(i)} \log[\sigma{(\theta^Tx^{(i)})}]+\left(1-y^{(i)}\right) \log [1-\sigma{(\theta^Tx^{(i)})}] +\end{aligned} +$$ +Remember:
+$$\sigma(z)' = \sigma(z)(1-\sigma(z)) $$ +All latest parametric supervised problems we have discussed are convex.
+The loss in function of the parameters is convex.
+GD gives you a global minimum/maximum on convex functions (optimization is easy)
+ +
# Generate a toy dataset, it's just a straight line with some Gaussian noise:
+xmin, xmax = -5, 5
+n_samples = 100
+np.random.seed(0)
+X = np.random.normal(size=n_samples)
+y = (X > 0).astype(float)
+X[X > 0] *= 4
+X += 0.3 * np.random.normal(size=n_samples)
+
+X = X[:, np.newaxis]
+
+plt.plot(X[y==1],[0]*sum(y==1),'.')
+plt.plot(X[y==0],[0]*sum(y==0),'r.');
+import numpy as np
+import matplotlib.pyplot as plt
+
+from sklearn.linear_model import LogisticRegression, LinearRegression
+from scipy.special import expit
+
+
+
+# Fit the classifier
+clf = LogisticRegression(C=1e5)
+clf.fit(X, y)
+
+# and plot the result
+plt.figure(1, figsize=(8, 6))
+plt.clf()
+plt.scatter(X.ravel(), y, color="black", zorder=20)
+X_test = np.linspace(-5, 10, 300)
+
+loss = expit(X_test * clf.coef_ + clf.intercept_).ravel()
+plt.plot(X_test, loss, color="red", linewidth=3)
+
+ols = LinearRegression()
+ols.fit(X, y)
+plt.plot(X_test, ols.coef_ * X_test + ols.intercept_, linewidth=1)
+plt.axhline(0.5, color=".5")
+
+plt.ylabel("y")
+plt.xlabel("X")
+plt.xticks(range(-5, 10))
+plt.yticks([0, 0.5, 1])
+plt.ylim(-0.25, 1.25)
+plt.xlim(-4, 10)
+plt.legend(
+ ("data","Logistic Regression Model", "Linear Regression Model"),
+ loc="lower right",
+ fontsize="small",
+)
+plt.tight_layout()
+plt.show()
+from sklearn.datasets import make_classification
+
+X, y = make_classification(
+ n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1, random_state=0, class_sep=0.8)
+plt.scatter(*X.T,c=y,cmap=cm.get_cmap("RdBu"));
+clf = LogisticRegression(penalty='none')
+clf.fit(X, y); minx, maxx = X.min(), X.max()
+support = np.linspace(minx, maxx, 100)
+xx, yy = np.meshgrid(support, support)
+points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+prob_mesh = clf.predict_proba(points)
+prob_mesh = prob_mesh[:,0].reshape(xx.shape)
+fig, axes = plt.subplots(1,2,figsize=(12,6))
+axes[0].contourf(xx,yy,prob_mesh,cmap=cm.get_cmap("RdBu"));axes[0].plot(0,0,'rx')
+axes[0].scatter(*X.T,c=(1-y),cmap=cm.get_cmap("RdBu"));
+axes[0].axis('scaled');axes[1].bar([0,1],clf.coef_[0]);axes[1].axis('equal');axes[1].set_xlim((-5,5));axes[1].set_ylim((-2,8));
+[1,0] and [0,1] are possible for 2 classes since it has to be a prob. distribution[1,1] is not a prob. distributionSo for a $K=2$ binary class problem,e.g. (spam vs not-spam) the possible labels could be:
+$$ y_{spam} = [1, 0]^T$$+$$ y_{not-spam} = [0, 1]^T$$
+ + +
+ +
+Who can tell me how we can compare two [discrete] probability distributions?
+
 +
+Objective: Estimate a sort of "distance" (or better divergence) between two distributions $p(x)$ vs $q(x)$.
+If we use $q(x)$ to construct a coding scheme for the purpose of transmitting values of $x$ to a receiver instead of $p(x)$, then the average additional amount of information required to specify the value of $x$ as a result of using $q(x)$ instead of the true distribution $p(x)$ is given by:
+$$ +\underbrace{H(P,Q)}_{\text{q not p, so extra}} - \underbrace{~~H(P)~~}_{\text{best we can do}} +$$Idea: if you use q instead of p, but the underlying process is governed by p, then you need to pay an extra price in transmission a bit more of information. "The bit more" is the equation above.
+ +We can use KL divergence!
+$$ +KL(P||Q) = H(P,Q) - H(P) = \underbrace{-\sum_{x \in X} p(x)\log q(x)}_{\text{cross-entropy}} - \underbrace{\big(-\sum_{x \in X} p(x)\log p(x)\big)}_{\text{entropy}} +$$ +Note that:
+Wait a second but....how much is the entropy of the "labels" aka entropy of $[0,1]$ or $[1,0]$?
+
+$$
+H(P,Q) - H(P) = \underbrace{-\sum_{x \in X} p(x)\log q(x)}_{\text{cross-entropy}} - \underbrace{\big(-\sum_{x \in X} p(x)\log p(x)\big)}_{\text{entropy of labels is zero}}
+$$
Maximizing Log Likelihood - I removed the sum over training samples for clarity
+$$ +\begin{aligned} +&\log L(\theta)= y^{(i)}\log p\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-p\left(x^{(i)}\right)\right) +\end{aligned} +$$Minimizing Cross-Entropy
+$$ \begin{aligned} +H(P,Q) - H(P) = \underbrace{-\sum_{y \in Y} p(y|x)\log q(y|x)}_{\text{cross-entropy}} \\ +-\Big(p(y=1)\log q(y=1|x)+p(y=0)\log q(y=0|x)\Big)\\ +-\Big(p(y=1)\log q(y=1|x)+(1-p(y=1))\log (1-q(y=1|x))\Big)\\ +-\Big(y\log q(y=1|x)+(1-y)\log (1-q(y=1|x))\Big)\\ +\end{aligned} $$ +Maximizing Log Likelihood
+$$y \log p\left(x\right)+\left(1-y\right) \log \left(1-p\left(x\right)\right) $$Minimizing Cross-Entropy +$$-\Big(y\log q(y=1|x)+(1-y)\log (1-q(y=1|x))\Big)$$
+ + +
+1 in the label.multiple choice questionsThe questions will be of increasing difficulties and calibrated to the test time.
+ +Given the following training data for a $\{0, 1\}$ binary classifier
+Determine the output of a K Nearest Neighbour (K-NN) classifier for all points on the interval $0 \le x \le 1$ using:
+Will be majority vote of class labels since we classify using all training points. Aka, we have two "1" and one "0". So always 1!
+ +A regressor algorithm is defined using the mean of the K Nearest Neighbours of a test point. Determine the ouput on the interval $0 \le x \le 1$ using the training data in the previous example for $K=2$.
+ +So we want to reduce 1) Misclassification or 2)Gini Impurity or 3) ? What else ?
+Know your enemy: the uniform distributions $\mbf{x} \sim\mathcal{U}$
+We want find a function $f(p)$ so that $f(p)$ is very distant from uniform distribution $Q$, so we can use KL divergence for this:
+$$ +KL(P||Q)= \sum_{k=1}^K p(x)\log \Big( \frac{p(x)}{1/K} \Big) = \sum_{k=1}^K p(x)\log\big(p(x)\big)-p(x)\log\big(1/K\big) +$$ +You and your best friend found a trick to save bandwidth over the internet. Instead of sharing a total of $N=10M$ grayscale images directly over the Internet, you took the $N$ images and learned $K=1000$ centroids $\{\mu_1,\ldots,\mu_{K}\}$ using K-means. Each input image is defined over the set $\mbf{x} \in [0,255]^{H\times W \times 1}$. +Then you shared once for all the $K$ centroids $\{\mu_k\}_{k=1}^{K}$ with your friend.
+Easy Questions: (check if you know the basic notions)
+More Difficult Questions: (check if you can reason on problems)
+You send $y$ associated to the image $\mbf{x}$, so $y$ takes value in $[1,K]$ and you friend can use $y$ to select the centroid nearest to the point $\mbf{x}$.
+In fact, the point $\mbf{x}$ was clustered in the cluster given by $y$.
+So one could stop here and say that the best approximation for $\mbf{x}$ is $\mu_{y}$ ($\mbf{x} \approx \mu_{y}$) but we can do more.
+Given that we have the scalar euclidean distance between $\mbf{x}$ and the associated centroid aka $\mu_{y}$ we have:
+$$ d= \vert \vert \mbf{x} -\mu_{y} \vert \vert_2$$We have only $d$ and $\mu_{y}$, the image $\mbf{x}$ that was sent is in the set:
+$$ \{\forall~\mbf{v} \in [0,255]^{H\times W \times 1}: \vert \vert \mbf{v} - \mu_y \vert \vert_2 = d \}$$which is all the points in the hyper-sphere in $[0,255]^{H\times W \times 1}$ of radius $d$ and centered at $\mu_y$
+ +You are hired by a famous company that has to compute $\ell_2^2$ norm over two feature vectors $\mbf{x} \in \mathbb{R}^{D}$ and $\mbf{y}\in \mathbb{R}^{D}$.
+The company works with a machine learning algorithm that guarantees that the features $\mbf{x}$ and $\mbf{y}$ lie on a unit hyper-sphere (_Hint: same as $\vert \vert x \vert\vert_2^2 =1$)_
+$$ d^2 = \vert \vert \mbf{x} - \mbf{y} \vert\vert_2^2 = \sum_{i=1}^D (x_i - y_i)^2$$(Hint: develop the definition of the norm written above)
+ +Using unit hyper-sphere: +$$1 + 1 - 2 \mbf{x}^T\mbf{y} = 2 - 2 \mbf{x}^T\mbf{y}$$
+So, yes, they can simply computing the dot product multiply by -2 and add 2.
+| Data Type $y$ | +Expo. Family | +Name | +
|---|---|---|
| $\{1,K\}$ | +Categorical | +Multi-class Classification | +
Regions of the space remains unclassified
+
$\mbf{x}$ is assigned to point with higher distance to the hyper-plane (because it is more confident to be that class).
+$\mbf{x}$ is assigned to point with lower distance to the hyper-plane (because it the least unsure).
+$\mbf{x}$ is assigned to point with lower distance to the hyper-plane (because it the least unsure).
+import numpy as np
+ww = [[1, 2], [-1, 4], [8, 2]]
+support = np.linspace(-10, 10, 100)
+xx, yy = np.meshgrid(support, support)
+W = np.array(ww)
+dim = xx.shape
+points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+dist = np.argmax((W@points.T), axis=0)
+dist = dist.reshape(dim)
+plt.figure(figsize=(7,7))
+plt.contourf(xx, yy, dist, cmap='jet')
+plt.plot(0, 0, 'rx')
+plt.axis('scaled')
+#plt.colorbar()
+plt.xlim(-10, 10);
+
Binary case: +$$ +\operatorname{sign}\big(\mbf{w}^T\mbf{x}_i + b\big) > 0 +$$
+$$\operatorname{sign}(z)= \begin{cases} +1, & \mbox{if } z\ge0 \\ +-1, & \mbox{if } z<0\end{cases}$$let's consider the distance as:
+We want:
+$$ \begin{cases} +\mbf{w}^T\mbf{x} + b > 0 \quad y=+1\\ +\mbf{w}^T\mbf{x} + b < 0 \quad y=-1\\ +\end{cases} $$ +Decision boundary $\{\mbf{w}_k,b_k\}_{k=1}^K$ per class given K classes.
+$$ \begin{align} +f_{\{\mbf{w}_1,b_1\}} = \mbf{w}_1^T\mbf{x} + b_1 \quad y=1\\ +f_{\{\mbf{w}_2,b_2\}} = \mbf{w}_2^T\mbf{x} + b_2 \quad y=2\\ +\cdots \\ +f_{\{\mbf{w}_K,b_K\}} = \mbf{w}_K^T\mbf{x} + b_K \quad y=K\\ +\end{align} $$ +Decision boundary $\{\mbf{w}_k,b_k\}_{k=1}^K$ per class given K classes.
+A data point $\mbf{x}^{\star}$ is assigned to class $\hat{k}$ iff:
+$$f_{\{\mbf{w}_\hat{k},b_\hat{k}\}}\big(\mbf{x}^{\star}\big) > f_{\{\mbf{w}_j,b_j\}}\big(\mbf{x}^{\star}\big) \quad \forall j \in \{1,\ldots K\} \setminus\{\hat{k}\} $$ +let's write it explicitly
+ +This has the same form as the decision boundary for the two-class case discussed before.
+ +The decision regions of such a discriminant are always singly connected and convex.
+Assuming $\mbf{x}_A$ and $\mbf{x}_B$ are in $\mathcal{R}_k$:
+$$ \begin{align} +(\mbf{w}_{k}-\mbf{w}_{j})^T{\mbf{x}_A} + (b_{k}- b_{j}) > 0 \quad \forall j\neq k\\ +(\mbf{w}_{k}-\mbf{w}_{j})^T{\mbf{x}_B} + (b_{k}- b_{j}) > 0 \quad \forall j\neq k\\ +\end{align} $$ +and also (definition of convexity): +$$ \hat{\mbf{x}} = \lambda\mbf{x}_A + (1-\lambda)\mbf{x}_B ~~~\text{with}~~~~ 0 \le \lambda \le 1$$
+Then also $\hat{\mbf{x}}$ is in $\mathcal{R}_k$, where $f_k(\cdot)$ is the hyper-plane: +$$ f_k(\hat{\mbf{x}}) > f_j(\hat{\mbf{x}})\quad \forall j\neq k$$
+
We have to show that: +$$ f_k(\hat{\mbf{x}}) > f_j(\hat{\mbf{x}})\quad \forall j\neq k$$
+and we know that $f_k({\mbf{x}}_A) > f_j({\mbf{x}}_A)$ and $f_k({\mbf{x}_B})>f_j({\mbf{x}_B}) ~~\forall j\neq k$ holds.
+We apply the definition and use linearity of hyper-plane (dot product):
+$$ \hat{\mbf{x}} = \lambda\mbf{x}_A + (1-\lambda)\mbf{x}_B ~~~\text{with}~~~~ 0 \le \lambda \le 1$$$$f_k(\hat{\mbf{x}})= f_k\Big( \lambda\mbf{x}_A + (1-\lambda)\mbf{x}_B\Big) = \lambda f_k( \mbf{x}_A) + (1-\lambda)f_k( \mbf{x}_B)$$ +Same hold for: +$$f_j(\hat{\mbf{x}})= f_k\Big( \lambda\mbf{x}_A + (1-\lambda)\mbf{x}_B\Big) = \lambda f_j( \mbf{x}_A) + (1-\lambda)f_j( \mbf{x}_B)$$
+Now this holds by assumption $$ f_k({\mbf{x}}_A) > f_j({\mbf{x}}_A) \quad \forall j\neq k$$ +given that $f_k({\mbf{x}_B})>f_j({\mbf{x}_B})$, it must be:
+$$ f_k({\mbf{x}}_A) + f_k({\mbf{x}_B}) > f_j({\mbf{x}}_A) + f_j({\mbf{x}_B}) \quad \forall j\neq k$$ +We have to prove: +$$f_k(\hat{\mbf{x}})= f_k\Big( \lambda\mbf{x}_A + (1-\lambda)\mbf{x}_B\Big) = \lambda f_k( \lambda\mbf{x}_A) + (1-\lambda)f_k( \lambda\mbf{x}_B)$$ +We arrived here: +$$ f_k({\mbf{x}}_A) + f_k({\mbf{x}_B}) > f_j({\mbf{x}}_A) + f_j({\mbf{x}_B}) \quad \forall j\neq k$$
+Remember $0 \le \lambda \le 1$ thus both $\lambda \ge 0$ and $(1-\lambda) \ge 0$, thus:
+
+$$ \underbrace{\lambda f_k({\mbf{x}}_A) + (1-\lambda)f_k({\mbf{x}_B})}_{f_k(\hat{\mbf{x}})} > \underbrace{\lambda f_j({\mbf{x}}_A) + (1-\lambda)f_j({\mbf{x}_B})}_{f_j(\hat{\mbf{x}})} \quad \forall j\neq k$$
Thus convex linear combination $\hat{\mbf{x}}$ still satisfy the same decision boundary:
+$$f_k(\hat{\mbf{x}}) > f_j(\hat{\mbf{x}}) \quad \forall j\neq k$$ +Decision boundary $\{\mbf{w}_k,b_k\}_{k=1}^K$ per class given K classes.
+$$ \begin{align} +f_{\{\mbf{w}_1,b_1\}} = \mbf{w}_1^T\mbf{x} + b_1 \quad y=1\\ +f_{\{\mbf{w}_2,b_2\}} = \mbf{w}_2^T\mbf{x} + b_2 \quad y=2\\ +\cdots \\ +f_{\{\mbf{w}_K,b_K\}} = \mbf{w}_K^T\mbf{x} + b_K \quad y=K\\ +\end{align} $$ +Decision boundary $\{\mbf{w}_k,b_k\}_{k=1}^K$ per class given K classes.
+We can model directly everything with a matrix:
+$$ \underbrace{\mbf{y}}_{\mathbb{R}^{Kx1}} = \underbrace{\mbf{W}}_{\mathbb{R}^{K\times d}}\underbrace{\mbf{x}}_{\mathbb{R}^{d\times1}} + \underbrace{\mbf{b}}_{\mathbb{R}^K}$$ +Will this work?
+$$ \underbrace{\mbf{Y}}_{\mathbb{R}^{Kxn}} = \underbrace{\mbf{W}}_{\mathbb{R}^{K\times d}}\underbrace{\mbf{X}}_{\mathbb{R}^{d\times n}} + \underbrace{\mbf{b}}_{\mathbb{R}^K}$$ +OK there is broadcasting on $\mbf{b}$!
+Can I just do
+y = np.argmax(W@points.T, axis=0)
+if I want to train a model?
+$$\arg\max_{\mbf{W},\mbf{b}}\Big[\arg\max_k \big(\mbf{W}\mbf{X} + \mbf{b} \big)\Big]$$ +argmax itself differentiable?¶import numpy as np
+from scipy.special import softmax
+_softmax = False
+ww = [[1, 2], [-1, 4], [8, 2]];support = np.linspace(-10, 10, 100)
+xx, yy = np.meshgrid(support, support)
+W = np.array(ww)
+dim = xx.shape
+points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+prob = np.argmax(W@points.T, axis=0) if not _softmax else np.max(np.tile(
+ np.arange(0, 3).T, (points.shape[0], 1)).T*softmax(0.2*W@points.T, axis=0), axis=0)
+prob = prob.reshape(dim)
+plt.figure(figsize=(7, 7));
+plt.contourf(xx, yy, prob, cmap='jet');plt.plot(0, 0, 'rx');plt.axis('scaled');plt.xlim(-10, 10);plt.figure(figsize=(7, 7));
+ax = plt.axes(projection='3d');ax.plot_surface(xx, yy, prob,rstride=1, cstride=1,cmap='jet', edgecolor='none');ax.view_init(30, -110)
+argmax itself differentiable? Nope!¶argmax with a smooth differentiable version called +SoftMax is rather a smooth approximation to the arg max function: the function whose value is which index has the maximum, modeled as One-Hot Encoding
+
Think Softmax as a differentiable selector!
+ +import numpy as np
+from scipy.special import softmax
+_softmax = True
+ww = [[1, 2], [-1, 4], [8, 2]]
+support = np.linspace(-10, 10, 100)
+xx, yy = np.meshgrid(support, support)
+W = np.array(ww)
+dim = xx.shape
+points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+prob = np.argmax(W@points.T, axis=0) if not _softmax else np.max(np.tile(
+ np.arange(0, 3).T, (points.shape[0], 1)).T*softmax(0.2*W@points.T, axis=0), axis=0)
+prob = prob.reshape(dim)
+plt.figure(figsize=(7, 7))
+plt.contourf(xx, yy, prob, cmap='jet')
+plt.plot(0, 0, 'rx')
+plt.axis('scaled')
+# plt.colorbar()
+plt.xlim(-10, 10);
+plt.figure(figsize=(7, 7))
+ax = plt.axes(projection='3d')
+ax.plot_surface(xx, yy, prob,rstride=1, cstride=1,
+ cmap='jet', edgecolor='none')
+ax.view_init(30, -130)
+argmax¶import numpy as np
+from scipy.special import softmax
+_softmax = True
+temperature = 10
+ww = [[1, 2], [-1, 4], [8, 2]]
+support = np.linspace(-10, 10, 100)
+xx, yy = np.meshgrid(support, support)
+W = np.array(ww)
+dim = xx.shape
+points = np.stack((xx.flatten(), yy.flatten()), axis=1)
+prob = np.argmax(points, axis=1) if not _softmax else np.max(np.tile(
+ np.arange(0, 2).T, (points.shape[0], 1))*softmax(temperature*points, axis=1), axis=1)
+prob = prob.reshape(dim)
+plt.figure(figsize=(4, 4))
+plt.contourf(xx, yy, prob, cmap='jet', levels=500)
+plt.plot(0, 0, 'rx');plt.axis('scaled');plt.xlim(-10, 10);plt.figure(figsize=(7, 7));ax = plt.axes(projection='3d')
+ax.plot_surface(xx, yy, prob,rstride=1, cstride=1,
+ cmap='jet', edgecolor='none')
+ax.view_init(30, 30)
+We model conditional probability of $y|x$:
+$$ \begin{cases} +p(y=1| \mbf{x};\mbf{W},\mbf{b}) = p_1 = \bmf{\sigma}_1\left( \mbf{W}\mbf{X} + \mbf{b} \right)\\ +p(y=2| \mbf{x};\mbf{W},\mbf{b}) = p_2 = \bmf{\sigma}_2\left( \mbf{W}\mbf{X} + \mbf{b} \right)\\ +\ldots \\ +p(y=K| \mbf{x};\mbf{W},\mbf{b}) = p_K = \bmf{\sigma}_K\left( \mbf{W}\mbf{X} + \mbf{b} \right)\\ +\end{cases} $$
+$$f_{\boldsymbol{\theta}}(\mbf{x}) \doteq \bmf{\sigma}\left( \mbf{W}\mbf{X} + \mbf{b} \right)$$
where:
+$$ \bmf{\sigma}_i(z)= \frac{e^{z_i}}{\sum_{k=1}^K e^{z_k}} \quad \text{Softmax function}$$ + +
+you can think $\mbf{z} = \mbf{W}\mbf{x}+\mbf{b}$ as unormalized log-probability of each class.
+
+$$ p(\mbf{y}| \mbf{x};\mbf{W},\mbf{b}) = \frac{\exp({\mbf{W}\mbf{x}+\mbf{b})}}{\sum_{k=1}^K\exp({\mbf{W}_k\mbf{x}+\mbf{b}_k)}} $$
you can think $\mbf{z} = \mbf{W}\mbf{x}+\mbf{b}$ as unormalized log-probability of each class.
+
+$$ p(\mbf{y}| \mbf{x};\mbf{W},\mbf{b}) = \frac{\exp({\mbf{W}\mbf{x}+\mbf{b})}}{\sum_{k=1}^K\exp({\mbf{W}_k\mbf{x}+\mbf{b}_k)}} $$
unormalized log-probability +{{np.random.seed(0);z = np.random.randn(10);_=plt.bar(range(z.size),z);}}
+ +{{np.random.seed(0);z = np.random.randn(10);_=plt.bar(range(z.size),z);}}
+ +{{np.random.seed(0);z = np.random.randn(10);_=plt.bar(range(z.size),softmax(z),color='r');}}
+ +np.random.seed(0)
+fig, axes = plt.subplots(1, 2, figsize=(5, 5))
+z = np.random.randn(10)
+axes[0].bar(range(z.size), z)
+axes[1].bar(range(z.size), softmax(z))
+# axes[0].axis('equal')
+# axes[1].axis('equal')
+axes[0].set(xlim=(-2,10), ylim=(0, 2))
+axes[1].set(xlim=(-2,10), ylim=(0, 2))
+axes[0].legend(['z'])
+axes[1].legend(['softmax']);
+fig.tight_layout()
+{{import numpy as np;import matplotlib.pyplot as plt;p = np.arange(1e-6, 1, 1e-2);y = -np.log(p);plt.figure(figsize=(7,7));plt.plot(p, y);_=plt.legend(['Crossentropy Loss in function of p']);}}
+ +Let's say that you have a model and you sample the weights $\mbf{W},\mbf{b}$ randomly from some distributions so that they are non zero. Also assume that the data $\mbf{x}$ is meaningful (non-zero).
++Can get you
+nanas $+\infty$ in the loss while you start training? +Or better, which is the value of the loss as soon as you start training?
nan as $+\infty$. +
+Yes, almost the same (up to save/wasted space)
+$$ p(\mbf{y}| \mbf{x};\mbf{W},\mbf{b}) = \frac{\exp({\mbf{W}\mbf{x}+\mbf{b})}}{\sum_{k=1}^K\exp({\mbf{W}_k\mbf{x}+\mbf{b}_k)}} $$Now $K=2$ and define $\mbf{z} \doteq \mbf{W}\mbf{x} + \mbf{b}$:
+$$ p(\mbf{y}=1| \mbf{x};\mbf{W},\mbf{b}) = \frac{\exp(\mbf{z}_1)}{\sum_{k=1}^K\exp(\mbf{z}_k)} = \frac{\exp(\mbf{z}_1)}{\exp(\mbf{z}_1) + \exp(\mbf{z}_2)} $$ +Yes it is the same but with sigmoid you spare a vector since $\mbf{W}$ becomes a single vector $\mbf{w}$ not a matrix!
+We can avoid modeling the other class since $ p(\mbf{y}=0| \mbf{x};\mbf{W},\mbf{b})=1- p(\mbf{y}=1| \mbf{x};\mbf{W},\mbf{b})$
+ +



 +
+
+
+
 +
+
+