本章将向您介绍旋转目标检测的基本概念,以及旋转目标检测的框架MMRotate,并提供了详细教程的链接。
受益于通用检测的蓬勃发展,目前绝大多数的旋转检测模型都是基于经典的通用检测器。随着检测任务的发展, 水平框在一些细分领域上已经无法满足研究人员的需求。通过重新定义目标表示形式以及增加回归自由度数量 的操作来实现旋转矩形框、四边形甚至任意形状检测,我们称之为旋转目标检测。如何更加高效地进行高精度 的旋转目标检测已成为当下的研究热点。下面列举一些旋转目标检测已经被应用或者有巨大潜力的领域: 人脸识别、场景文字、遥感影像、自动驾驶、医学图像、机器人抓取等。
旋转目标检测与通用目标检测最大的不同就是用旋转框标注来代替水平框标注,它们的定义如下:
- 水平框: 宽沿x轴方向,高沿y轴方向的矩形。通常可以用2个对角顶点的坐标表示
(x_i, y_i)(i = 1, 2),也可以用中心点坐标以及宽和高表示(x_center, y_center, height, width)。 - 旋转框: 由水平框绕中心点旋转一个角度
angle得到,通过添加一个弧度参数得到其旋转框定义法(x_center, y_center, height, width, theta)。其中,theta = angle * pi / 180, 单位为rad。当旋转的角度为90°的倍数时,旋转框退化为水平框。标注软件导出的旋转框标注通常为多边形(xr_i, yr_i)(i = 1, 2, 3, 4),在训练时需要转换为旋转框定义法。
在 MMRotate 中,角度参数的单位均为弧度。
旋转框可以由水平框绕其中心点顺时针旋转或逆时针旋转得到。旋转方向和坐标系的选择密切相关。
图像空间采用右手坐标系(y,x),其中 y 是上->下,x 是左->右。
此时存在2种相反的旋转方向:
- 顺时针(CW)
CW 的示意图
0-------------------> x (0 rad)
| A-------------B
| | |
| | box h
| | angle=0 |
| D------w------C
v
y (pi/2 rad)
CW 的旋转矩阵
\begin{pmatrix}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{pmatrix}
CW 的旋转变换
P_A=
\begin{pmatrix} x_A \\ y_A\end{pmatrix}
=
\begin{pmatrix} x_{center} \\ y_{center}\end{pmatrix} +
\begin{pmatrix}\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha\end{pmatrix}
\begin{pmatrix} -0.5w \\ -0.5h\end{pmatrix} \\
=
\begin{pmatrix} x_{center}-0.5w\cos\alpha+0.5h\sin\alpha
\\
y_{center}-0.5w\sin\alpha-0.5h\cos\alpha\end{pmatrix}
- 逆时针(CCW)
CCW 的示意图
0-------------------> x (0 rad)
| A-------------B
| | |
| | box h
| | angle=0 |
| D------w------C
v
y (-pi/2 rad)
CCW 的旋转矩阵
\begin{pmatrix}
\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha
\end{pmatrix}
CCW 的旋转变换
P_A=
\begin{pmatrix} x_A \\ y_A\end{pmatrix}
=
\begin{pmatrix} x_{center} \\ y_{center}\end{pmatrix} +
\begin{pmatrix}\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha\end{pmatrix}
\begin{pmatrix} -0.5w \\ -0.5h\end{pmatrix} \\
=
\begin{pmatrix} x_{center}-0.5w\cos\alpha-0.5h\sin\alpha
\\
y_{center}+0.5w\sin\alpha-0.5h\cos\alpha\end{pmatrix}
在MMCV中可以设置旋转方向的算子有:
- box_iou_rotated (默认为
CW) - nms_rotated (默认为
CW) - RoIAlignRotated (默认为
CCW) - RiRoIAlignRotated (默认为
CCW)。
在MMRotate中,旋转框的旋转方向均为`CW`。
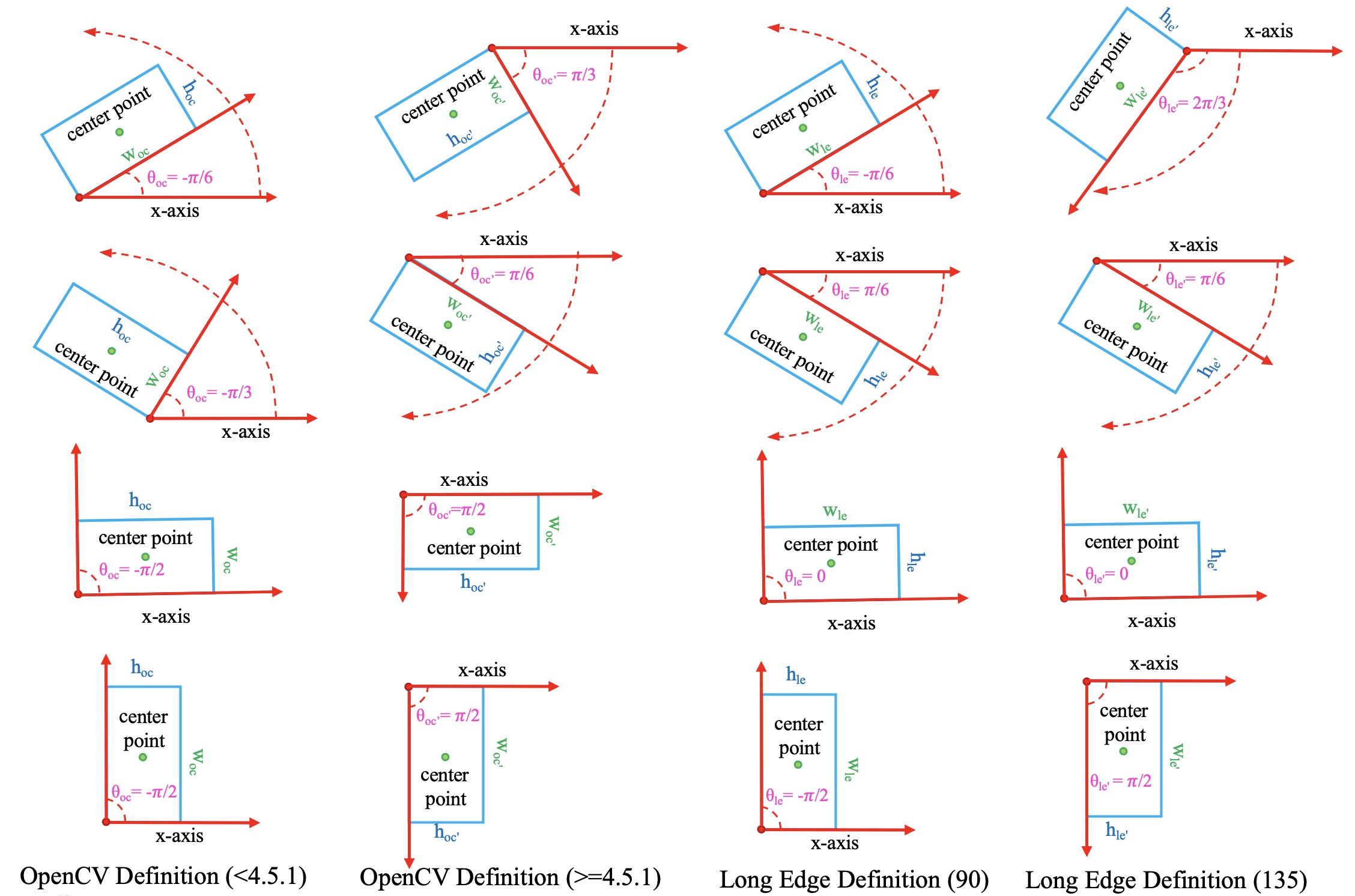
由于 theta 定义范围的不同,在旋转目标检测中逐渐派生出如下3种旋转框定义法:
- {math}
D_{oc^{\prime}}: OpenCV 定义法,angle∈(0, 90°],theta∈(0, pi / 2], height 与 x 正半轴之间的夹角为正的锐角。该定义法源于OpenCV中的cv2.minAreaRect函数, 其返回值为(0, 90°]。 - {math}
D_{le135}: 长边135°定义法,angle∈[-45°, 135°),theta∈[-pi / 4, 3 * pi / 4)并且height > width。 - {math}
D_{le90}: 长边90°定义法,angle∈[-90°, 90°),theta∈[-pi / 2, pi / 2)并且height > width。
三种定义法之间的转换关系在MMRotate内部并不涉及,因此不多做介绍。如果想了解更多的细节,可以参考这篇博客。
MMRotate同时支持上述三种旋转框定义法,可以通过配置文件灵活切换。
需要注意的是,在4.5.1之前的版本中,cv2.minAreaRect的返回值为[-90°, 0°)
(参考资料)。为了便于区分,
将老版本的OpenCV定义法记作 {math}D_{oc}。
- {math}
D_{oc^{\prime}}: OpenCV 定义法,opencv>=4.5.1,angle∈(0, 90°],theta∈(0, pi / 2]。 - {math}
D_{oc}: 老版的 OpenCV 定义法,opencv<4.5.1,angle∈[-90°, 0°),theta∈[-pi / 2, 0)。
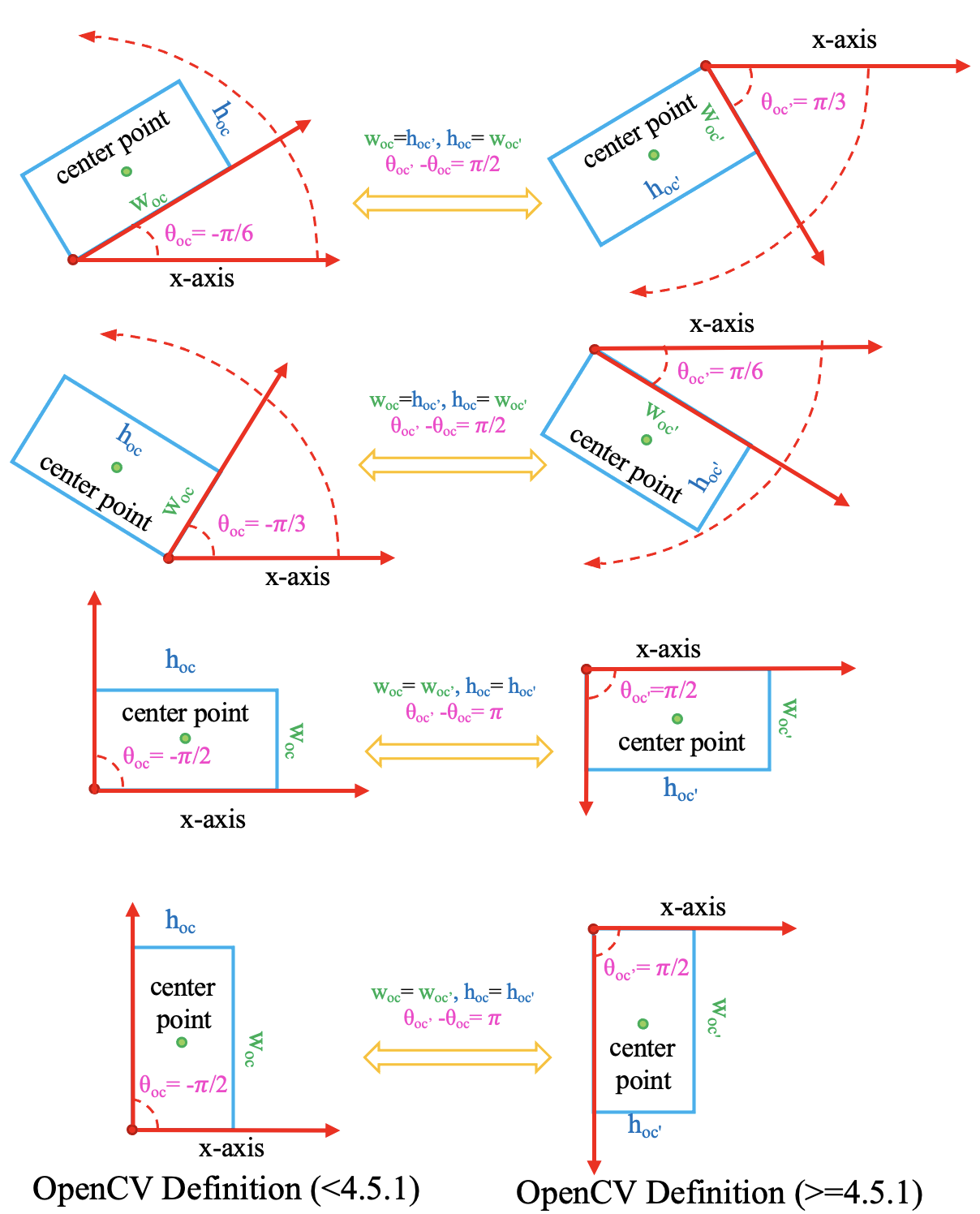
两种 OpenCV 定义法的转换关系如下:
D_{oc^{\prime}}\left( h_{oc^{\prime}},w_{oc^{\prime}},\theta _{oc^{\prime}} \right) =\begin{cases}
D_{oc}\left( w_{oc},h_{oc},\theta _{oc}+\pi /2 \right) , otherwise\\
D_{oc}\left( h_{oc},w_{oc},\theta _{oc}+\pi \right) ,\theta _{oc}=-\pi /2\\
\end{cases}
\\
D_{oc}\left( h_{oc},w_{oc},\theta _{oc} \right) =\begin{cases}
D_{oc^{\prime}}\left( w_{oc^{\prime}},h_{oc^{\prime}},\theta _{oc^{\prime}}-\pi /2 \right) , otherwise\\
D_{oc^{\prime}}\left( h_{oc^{\prime}},w_{oc^{\prime}},\theta _{oc^{\prime}}-\pi \right) , \theta _{oc^{\prime}}=\pi /2\\
\end{cases}
不管您使用的 OpenCV 版本是多少, MMRotate 都会将 OpenCV 定义法的 theta 转换为 (0, pi / 2]。
评估 mAP 的代码中涉及 IoU 的计算,可以直接计算旋转框 IoU,也可以将旋转框转换为多边形,然后 计算多边形 IoU (DOTA在线评估使用的是计算多边形 IoU)。
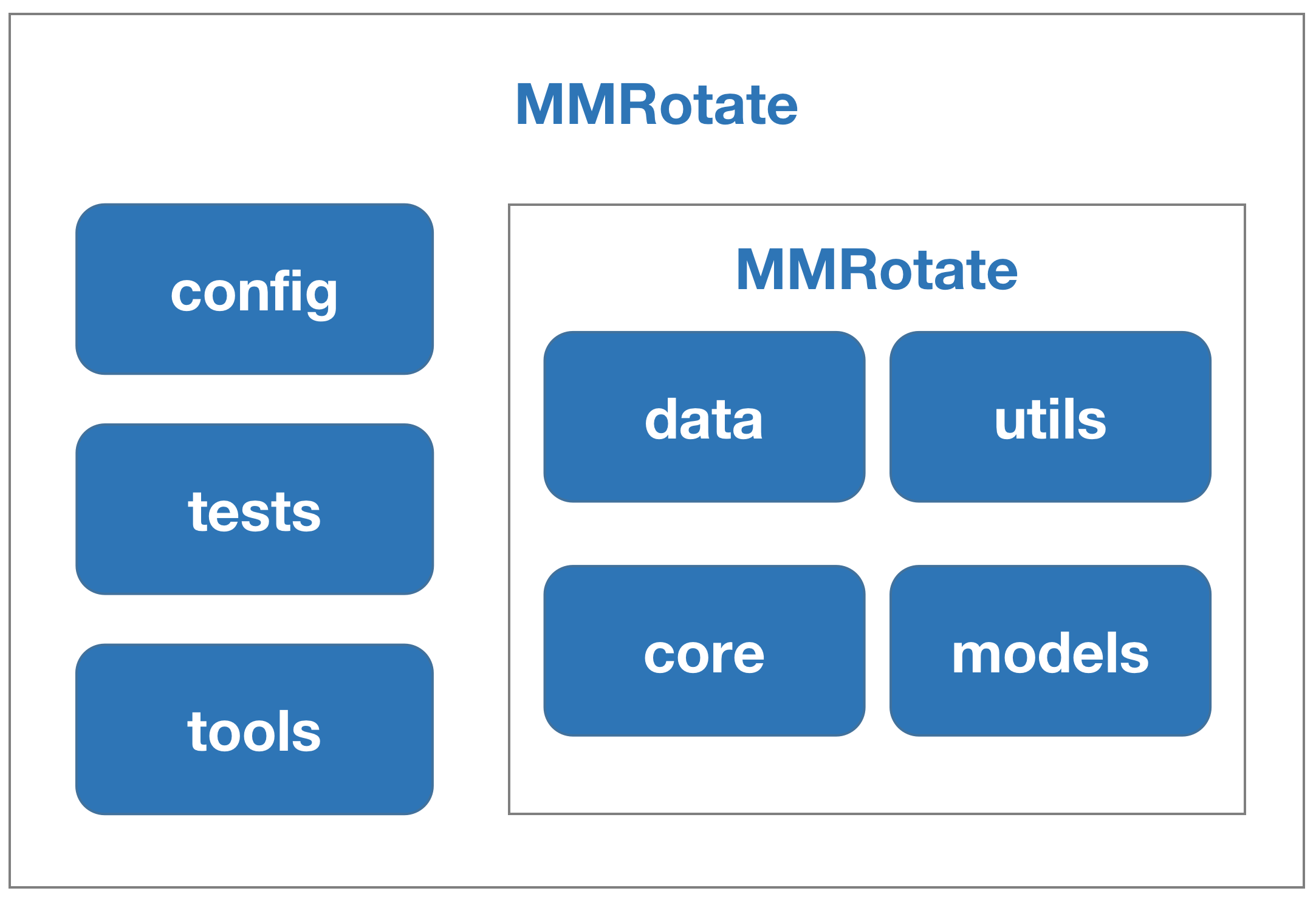
MMRotate 是一个为旋转目标检测方法提供统一训练和评估框架的工具箱,以下是其整体框架::
MMRotate 包括四个部分, datasets, models, core and apis.
-
datasets用于数据加载和数据增强。 在这部分,我们支持了各种旋转目标检测数据集和数据增强预处理。 -
models包括模型和损失函数。 -
core为模型训练和评估提供工具。 -
apis为模型训练、测试和推理提供高级API。
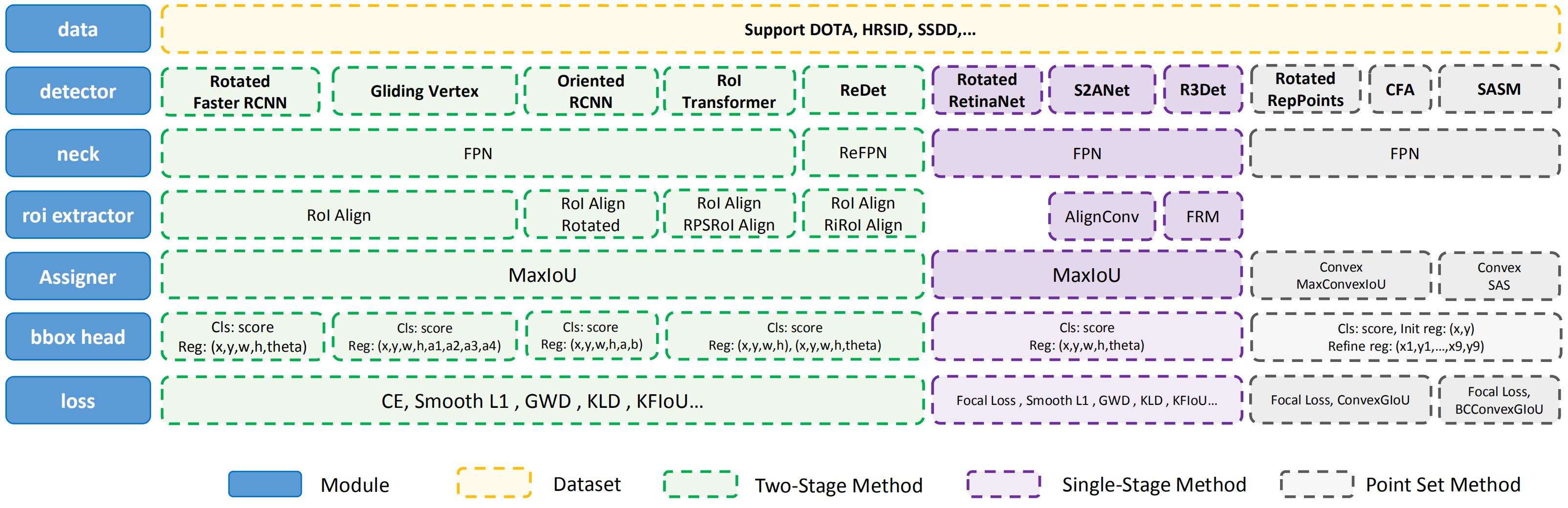
MMRotate 的模块设计如下图所示:
其中由于旋转框定义法不同而需要注意的地方有如下几个:
- 读取标注
- 数据增强
- 指派样本
- 评估指标
下面是 MMRotate 详细的分步指南: