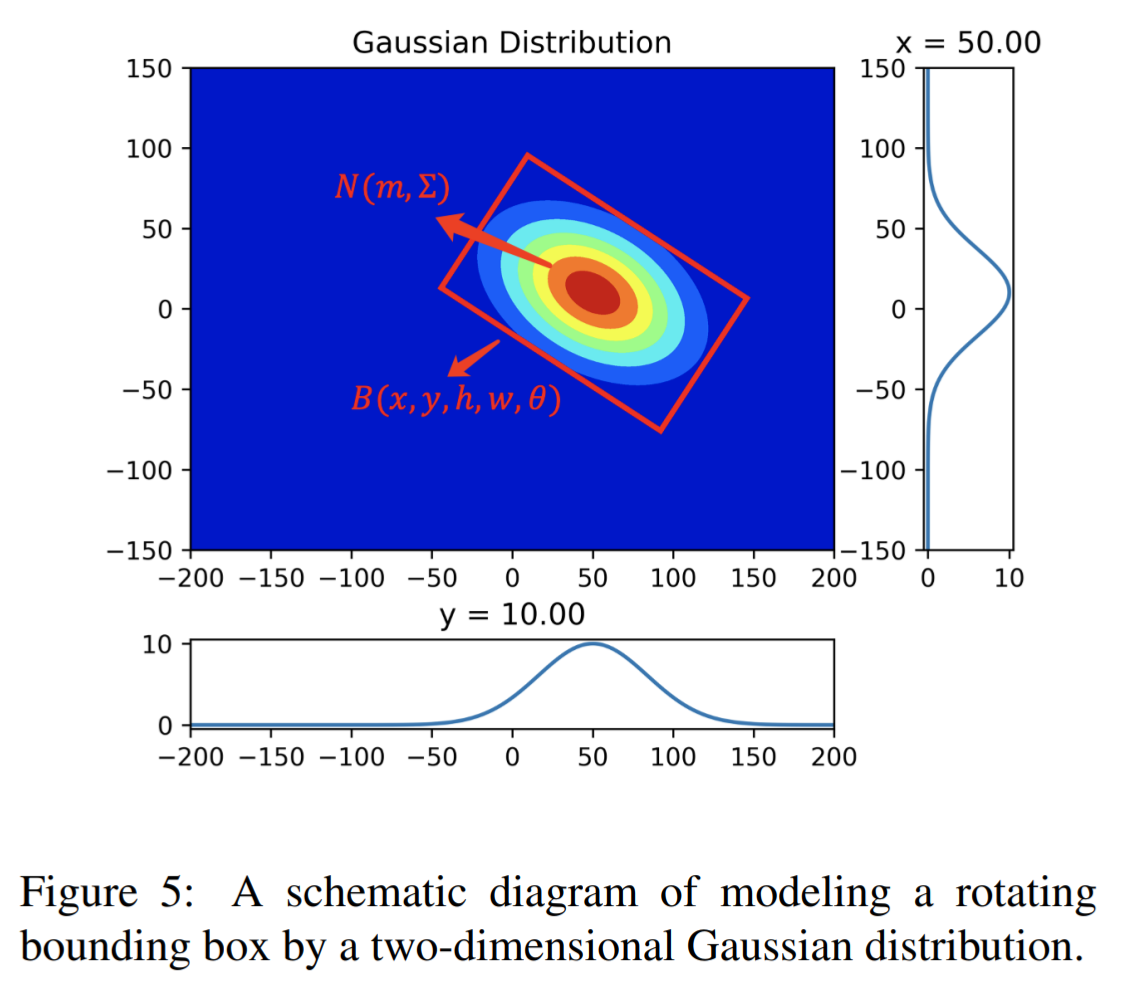
Boundary discontinuity and its inconsistency to the final detection metric have been the bottleneck for rotating detection regression loss design. In this paper, we propose a novel regression loss based on Gaussian Wasserstein distance as a fundamental approach to solve the problem. Specifically, the rotated bounding box is converted to a 2- D Gaussian distribution, which enables to approximate the indifferentiable rotational IoU induced loss by the Gaussian Wasserstein distance (GWD) which can be learned efficiently by gradient back-propagation. GWD can still be informative for learning even there is no overlapping between two rotating bounding boxes which is often the case for small object detection. Thanks to its three unique properties, GWD can also elegantly solve the boundary discontinuity and square-like problem regardless how the bounding box is defined. Experiments on five datasets using different detectors show the effectiveness of our approach.
| Backbone | mAP | Angle | lr schd | Mem (GB) | Inf Time (fps) | Aug | Batch Size | Configs | Download |
|---|---|---|---|---|---|---|---|---|---|
| ResNet50 (1024,1024,200) | 64.55 | oc | 1x | 3.38 | 14.8 | - | 2 | rotated_retinanet_hbb_r50_fpn_1x_dota_oc | model | log |
| ResNet50 (1024,1024,200) | 69.55 | oc | 1x | 3.39 | 14.8 | - | 2 | rotated_retinanet_hbb_gwd_r50_fpn_1x_dota_oc | model | log |
@inproceedings{yang2021rethinking,
title={Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss},
author={Yang, Xue and Yan, Junchi and Qi, Ming and Wang, Wentao and Xiaopeng, Zhang and Qi, Tian},
booktitle={International Conference on Machine Learning},
year={2021}
}