README.md

919. Complete Binary Tree Inserter

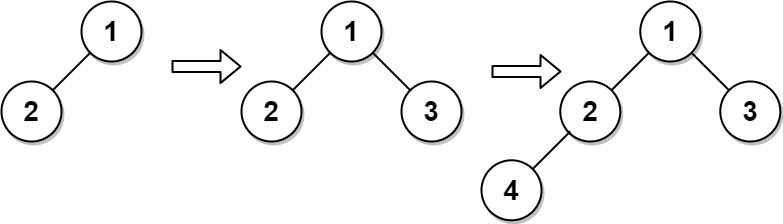
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.

Implement the CBTInserter class:

• CBTInserter(TreeNode root) Initializes the data structure with the root of the complete binary tree.
• int insert(int v) Inserts a TreeNode into the tree with value Node.val == val so that the tree remains complete, and returns the value of the parent of the inserted TreeNode.
• TreeNode get_root() Returns the root node of the tree.

Example 1:

Input:
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
Output:
[null, 1, 2, [1, 2, 3, 4]]
Explanation:
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3);  // return 1
cBTInserter.insert(4);  // return 2
cBTInserter.get_root(); // return [1, 2, 3, 4]

Constraints:

• The number of nodes in the tree will be in the range [1, 1000].
• 0 <= Node.val <= 5000
• root is a complete binary tree.
• 0 <= val <= 5000
• At most 104</sup calls will be made to insert and get_root.

Solutions (Python)

1. Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class CBTInserter:

    def __init__(self, root: Optional[TreeNode]):
        self.root = root
        self.size = 0
        stack = [root]

        while stack:
            node = stack.pop()

            if node:
                self.size += 1
                stack.append(node.left)
                stack.append(node.right)

    def insert(self, val: int) -> int:
        self.size += 1
        size = self.size
        node = self.root
        stack = []

        while size > 1:
            stack.append(size & 1)
            size >>= 1

        while len(stack) > 1:
            node = node.left if stack.pop() == 0 else node.right

        if stack.pop() == 0:
            node.left = TreeNode(val)
        else:
            node.right = TreeNode(val)

        return node.val

    def get_root(self) -> Optional[TreeNode]:
        return self.root

# Your CBTInserter object will be instantiated and called as such:
# obj = CBTInserter(root)
# param_1 = obj.insert(val)
# param_2 = obj.get_root()