README.md

812. Largest Triangle Area

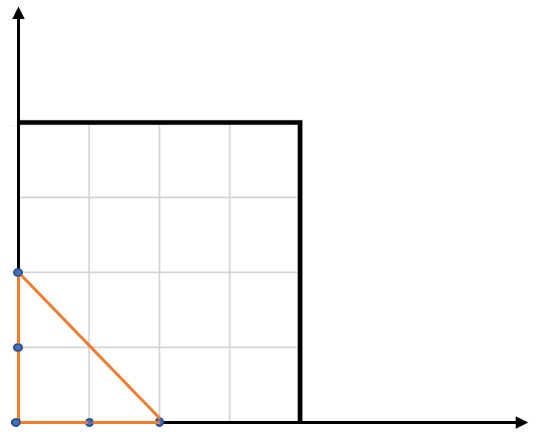
You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation:
The five points are show in the figure below. The red triangle is the largest.

Notes:

• 3 <= points.length <= 50.
• No points will be duplicated.
• -50 <= points[i][j] <= 50.
• Answers within 10^-6 of the true value will be accepted as correct.

Solutions (Rust)

1. Brute Force

impl Solution {
    pub fn largest_triangle_area(points: Vec<Vec<i32>>) -> f64 {
        let mut max_area = 0_f64;

        for i in 0..(points.len() - 2) {
            let a = &points[i];
            for j in (i + 1)..(points.len() - 1) {
                let b = &points[j];
                for k in (j + 1)..points.len() {
                    let c = &points[k];
                    max_area = max_area.max(Self::area(a, b, c));
                }
            }
        }

        max_area
    }
    
    pub fn area(a: &Vec<i32>, b: &Vec<i32>, c: &Vec<i32>) -> f64 {
        (a[0] * b[1] + b[0] * c[1] + c[0] * a[1] -
        a[1] * b[0] - b[1] * c[0] - c[1] * a[0]).abs() as f64 / 2.0
    }
}