README.md

576. Out of Boundary Paths

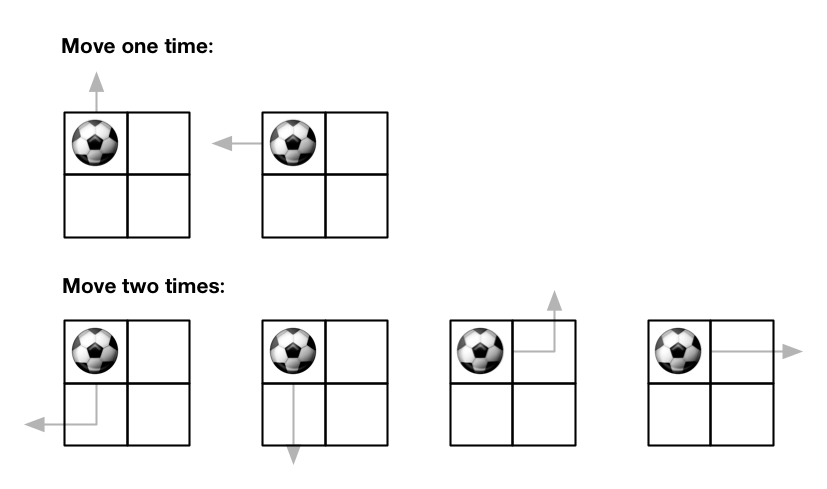
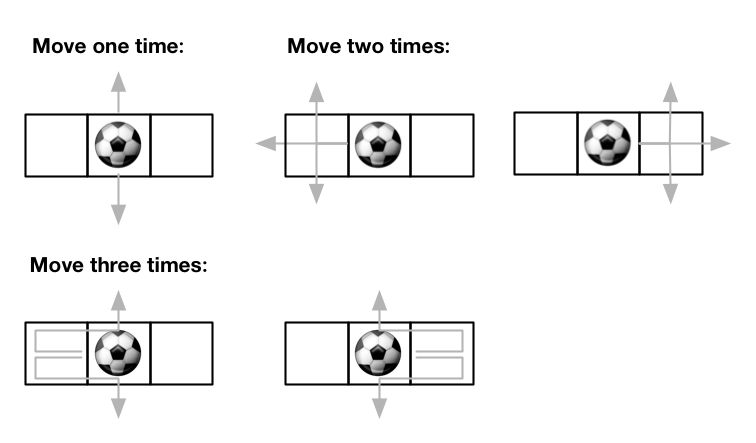
There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent four cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.

Example 1:

Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6

Example 2:

Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12

Constraints:

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow <= m
• 0 <= startColumn <= n

Solutions (Rust)

1. Dynamic Programming

impl Solution {
    pub fn find_paths(m: i32, n: i32, max_move: i32, start_row: i32, start_column: i32) -> i32 {
        let mut dp0 = vec![vec![0; n as usize]; m as usize];
        dp0[start_row as usize][start_column as usize] = 1;
        let mut ret = 0;

        for _ in 0..max_move {
            let mut dp1 = vec![vec![0; n as usize]; m as usize];

            for r in 0..m as usize {
                for c in 0..n as usize {
                    if r > 0 {
                        dp1[r - 1][c] = (dp1[r - 1][c] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if c > 0 {
                        dp1[r][c - 1] = (dp1[r][c - 1] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if r + 1 < m as usize {
                        dp1[r + 1][c] = (dp1[r + 1][c] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                    if c + 1 < n as usize {
                        dp1[r][c + 1] = (dp1[r][c + 1] + dp0[r][c]) % 1_000_000_007;
                    } else {
                        ret = (ret + dp0[r][c]) % 1_000_000_007;
                    }
                }
            }

            dp0 = dp1;
        }

        ret
    }
}