README_EN.md

comments	difficulty	edit_url
true	Medium	https://github.com/doocs/leetcode/edit/main/lcci/16.20.T9/README_EN.md

16.20. T9

中文文档

Description

On old cell phones, users typed on a numeric keypad and the phone would provide a list of words that matched these numbers. Each digit mapped to a set of 0 - 4 letters. Implement an algo­rithm to return a list of matching words, given a sequence of digits. You are provided a list of valid words. The mapping is shown in the diagram below:


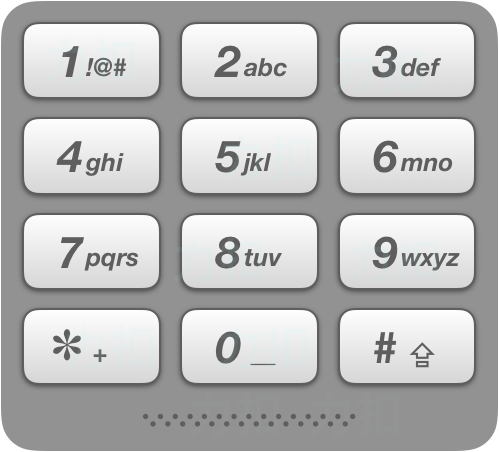Example 1:

Input: num = "8733", words = ["tree", "used"]
Output: ["tree", "used"]

Example 2:

Input: num = "2", words = ["a", "b", "c", "d"]
Output: ["a", "b", "c"]

Note:

• num.length <= 1000
• words.length <= 500
• words[i].length == num.length
• There are no number 0 and 1 in num.

Solutions

Solution 1: Reverse Thinking

We consider a forward solution, which traverses each digit in the string $num$, maps it to the corresponding letter, combines all the letters to obtain all possible words, and then compares them with the given word list. If the word is in the list, it is added to the answer. The time complexity of this solution is $O(4^n)$, where $n$ is the length of the string $num$, which will obviously time out.

Instead, we can consider a reverse solution, which traverses the given word list, and for each word $w$, determines whether it can be composed of the digits in the string $num$. If it can be composed, it is added to the answer. The key to the problem is how to determine whether a word can be composed of the digits in the string $num$. We only need to traverse each letter in the word $w$, restore it to the corresponding digit, and compare it with each digit in the string $num$ one by one. If they are the same, it means that the word $w$ can be composed of the digits in the string $num$.

The time complexity is $O(m \times n)$, and the space complexity is $O(C)$. Here, $m$ and $n$ are the length of the word list and the string $num$, respectively, and $C$ is the size of the character set, which is $26$ in this problem.

Python3

class Solution:
    def getValidT9Words(self, num: str, words: List[str]) -> List[str]:
        def check(w: str) -> bool:
            return all(d[c] == num[i] for i, c in enumerate(w))

        d = {c: d for c, d in zip(ascii_lowercase, "22233344455566677778889999")}
        return [w for w in words if check(w)]

Python3

class Solution:
    def getValidT9Words(self, num: str, words: List[str]) -> List[str]:
        trans = str.maketrans(ascii_lowercase, "22233344455566677778889999")
        return [w for w in words if w.translate(trans) == num]

Java

class Solution {
    public List<String> getValidT9Words(String num, String[] words) {
        String s = "22233344455566677778889999";
        int[] d = new int[26];
        for (int i = 0; i < 26; ++i) {
            d[i] = s.charAt(i);
        }
        List<String> ans = new ArrayList<>();
        int n = num.length();
        for (String w : words) {
            boolean ok = true;
            for (int i = 0; i < n; ++i) {
                if (d[w.charAt(i) - 'a'] != num.charAt(i)) {
                    ok = false;
                    break;
                }
            }
            if (ok) {
                ans.add(w);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<string> getValidT9Words(string num, vector<string>& words) {
        string s = "22233344455566677778889999";
        int d[26];
        for (int i = 0; i < 26; ++i) {
            d[i] = s[i];
        }
        vector<string> ans;
        int n = num.size();
        for (auto& w : words) {
            bool ok = true;
            for (int i = 0; i < n; ++i) {
                if (d[w[i] - 'a'] != num[i]) {
                    ok = false;
                }
            }
            if (ok) {
                ans.emplace_back(w);
            }
        }
        return ans;
    }
};

Go

func getValidT9Words(num string, words []string) (ans []string) {
	s := "22233344455566677778889999"
	d := [26]rune{}
	for i, c := range s {
		d[i] = c
	}
	for _, w := range words {
		ok := true
		for i, c := range w {
			if d[c-'a'] != rune(num[i]) {
				ok = false
				break
			}
		}
		if ok {
			ans = append(ans, w)
		}
	}
	return
}

TypeScript

function getValidT9Words(num: string, words: string[]): string[] {
    const s = '22233344455566677778889999';
    const d: string[] = Array(26);
    for (let i = 0; i < 26; ++i) {
        d[i] = s[i];
    }
    const ans: string[] = [];
    const n = num.length;
    for (const w of words) {
        let ok = true;
        for (let i = 0; i < n; ++i) {
            if (d[w[i].charCodeAt(0) - 97] !== num[i]) {
                ok = false;
                break;
            }
        }
        if (ok) {
            ans.push(w);
        }
    }
    return ans;
}

Swift

class Solution {
    func getValidT9Words(_ num: String, _ words: [String]) -> [String] {
        let s = "22233344455566677778889999"
        var d = Array(repeating: 0, count: 26)
        for i in 0..<26 {
            d[i] = Int(s[s.index(s.startIndex, offsetBy: i)].asciiValue! - Character("0").asciiValue!)
        }
        var ans: [String] = []
        let n = num.count
        for w in words {
            var ok = true
            for i in 0..<n {
                let numChar = Int(num[num.index(num.startIndex, offsetBy: i)].asciiValue! - Character("0").asciiValue!)
                if d[Int(w[w.index(w.startIndex, offsetBy: i)].asciiValue! - Character("a").asciiValue!)] != numChar {
                    ok = false
                    break
                }
            }
            if ok {
                ans.append(w)
            }
        }
        return ans
    }
}