| layout | title | permalink |
|---|---|---|
default |
Voting Systems Simulation |
fr/Voting-Systems-Simulation |
Simulation de diverses systèmes de votes
Check out on GitHub
Documentation :
Ce dépôt contient un script qui réalise des simulations de diverses méthodes de scrutin sur des données générées aléatoirement.
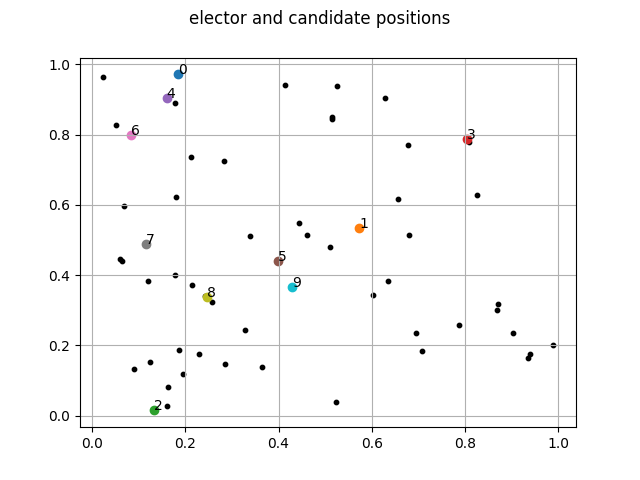
Les opinions sur le sujet de votre choix sont représentées comme des points dans un espace vectoriel de dimension finie. Cela signifie que les positions des électeurs et des candidats sont représentées comme des coordonnées dans un espace vectoriel qui peut être un plan, un espace en trois dimensions, ou plus.
Voici une image de ce à quoi ça ressemble
Les buts de cette simulaiton sont de voir s'il existe des différences entre les méthodes de vote, et si ces différences existent, déterminer lesquelles sont les meilleures.
Si vous êtes juste intéressés par les résultats et que vous avez entièrement confiance, vous pouvez lire la section Travaux connexes puis passer directement à la section Interprétation des résultats.
Vous pourriez également être intéressé par cet article qui compare de nombreuses méthodes de vote, en expliquant comment elles fonctionnent et quels sont leurs défauts.d their flaws.
Cette simulation est inspirée par diverses vidéos
- (EN / FR sub) Simulating alternate voting systems par Primer
- (FR / EN sub) Réformons l'élection présidentielle ! par ScienceEtonnante
- (FR / EN sub) Monsieur le président, avez-vous vraiment gagné cette élection ? par La statistique expliquée à mon chat
- (FR) Le MEILLEUR système de vote (et pourquoi c'est une mauvaise question) par Tzitzimitl - Esprit Critique
Si vous voulez lancer la simulation, vous pouvez faire comme suit
git clone https://github.com/Relex12/Voting-Systems-Simulation.git
cd Voting-Systems-Simulation
python3 simulation.py
Ce qui vous donnera quelque chose de similaire à ceci
plurality: 6
two round: 9
instant runoff: 9
condorcet: 3
borda: 3
approval: 3
majority judgement: 3
et produira une image dans img/position.png de la position des électeurs et des candidats.
Vous pouvez afficher le message d'erreur en lançant la commande : python3 simulation.py -h
usage: simulation.py [-h] [-v] [-d DIMENSION] [-e ELECTORS] [-c CANDIDATES]
[-t THRESHOLD] [--noplot] [-r REPEAT] [-o OUTPUT]
[--test TEST]
optional arguments:
-h, --help show this help message and exit
-v, --version show program's version number and exit
-d DIMENSION, --dimension DIMENSION
number of dimensions to use
-e ELECTORS, --electors ELECTORS
number of electors for the simulation
-c CANDIDATES, --candidates CANDIDATES
number of candidates for the simulation
-t THRESHOLD, --threshold THRESHOLD
rejection threshold for scoring methods
--noplot creates the positions image
-r REPEAT, --repeat REPEAT
number of repetitions of the simulation
-o OUTPUT, --output OUTPUT
output file to write the results
--test TEST number of times to test the method given in the test()
function
Le code est séparé en deux modules
simulation.pyest le module principal, il va soit calculer le taux d'indécidabilité de la méthode de vote donnée dans le code source si--testest donné comme argument (test()), soit lancer la simulation, premièrement en tirant au hasard les positions des électeurs et des candidats (initiate_dict()), puis en affichant ces positions danspositions.png(plot_grid()), enfin en calculant les distances entre les électeurs et les candidats (distances()) avant de faire appel aux méthodes de vote.voting.pyest le module qui contient les fonctions pour élire un candidat basé sur les préférences des électeurs, des détails sur l'implémentation et les algorithmes sont disponibles dans la documentation.
La documentation des modules simulation.py et voting.py est construite avec pdoc3. Elle est disponible dans le dossier doc/ du dépôt. Vous pouvez la consulter en ligne
Pour générer la documentation, lancez la commande pdoc --html -o doc/ *.py . Vous pouvez aussi la regarder dans votre navigateur à l'adresse localhost:8080 en exécutant pdoc --http : *.py.
Parfois, certaines méthodes ne sont juste pas capable de sélectionner un vainqueur, à cause du paradoxe de Condorcet ou à cause de cas d'égalité. Quand cela arrive, un objet None est retourné par la méthode correspondante. Pour estimer ce taux, les méthodes ont été testées 100000 (cent mille) fois chacune, en utilisant l'argument de ligne de commande --test, avec les valeurs par défaut de 2 dimensions, 50 électeurs et 10 candidats.
Voici les résultats
| Méthode | Nom français | Taux estimé (%) |
|---|---|---|
| Plurality | Scrutin majoritaire à un tour | 0.0 |
| Two rounds | Scrutin majoritaire à deux tours | 0.0 |
| Instant Runoff | Vote alternatif | 0.0 |
| Condorcet | Méthode de Condorcet | 2.11 |
| Borda | Méthode de Borda | 0.002 |
| Approval | Vote par approbation | 11.235 |
| Majority jugement | Jugement majoritaire | 2.01 |
Notes :
- Pour les scrutins majoritaires à un et deux tours et le vote alternatif, les cas d'égalité ne se produisent que s'il y a une égalité stricte lors du dernier tour, ce qui est très improbable.
- Pour la méthode de Borda, les cas d'égalité arrivaient trop souvent, il a donc été décidé de réaliser un duel de Condorcet entre les candidats vainqueurs. C'est pourquoi le taux d'indécidabilité est aussi bas, cela n'arrive que lors que la méthode de Borda et celle de Condorcet ne peuvent décider.
- Pour le vote par approvation, le haut taux d'indécidabilité est dû au trop faible nombre d'électeurs. Si on réalise le test le même nombre de fois avec 200 électeurs, ce taux chute à 2.97%.
Avant de lire l'interprétation des résultats, il y a quelques défauts que vous pourriez avoir envie de connaître. Ces défauts de signifient pas que la simulation est mauvaise, simplement que dans une problématique du monde réel, une telle approche ne pourrait être utilisée que par une entité omnisciente, ou alors va probablement produire des écarts significatifs avec les résultats observés.
- Représentation dimensionnelle : Il pourrait être une assez mauvaise simplification de représenter la position de chacun, candidat ou électeur, dans un espace vectoriel à plusieurs dimensions. Même avec un grand nombre de dimensions, il pourrait être impossible de convertir une opinion, quelque soit le sujet, en un vecteur fini. De plus, certaines variables pourraient être qualitatives au lieu de quantitatives.
- Évaluation omnisciente des positions : Aussi complexe que peut être une opinion, on considère que tout le monde, électeurs et candidats, ont l'exacte même connaissance de la position des autres. l'effet de ce défaut augment avec le nombre de dimensions : si vous devez placer des opinions dans un espace vectoriel, ce sera plus facile avec le moins de dimensions possible. Ce défaut est donc incompatible avec le précédent.
- Répartition uniforme : Les positions sont tirées au hasard de manière uniforme entre les deux valeurs extrêmes, ce qui ne reflète pas la réalité. Si vous réalisez une étude statistique sur l'opinion des gens sur un sujet donné, peu importe ce que c'est, vous allez très probablement observer des corrélations entre les variables. Ces corrélations implique que certaines positions sur certaines variables vont augmenter les chances d'avoir telle position sur une autre variable. Ces corrélations mènent à la présence de zones vides dans l'espace vectoriel.
- Importance uniforme des variables Différentes variables sur différentes dimensions pourraient ne pas avoir le même point dans le calcul des distances, car certaines variables peuvent avoir des importances ou des échelles différentes. Encore plus important, ces différents poids pourraient dépendre de la position sur d'autres variables.
- Pas de pression sociale : Les vraies personnes de la vraie vivent peuvent ajuster légèrement leur position de vote selon leur environnement, par exemple les positions de la famille et des amis. Ceci pourrait mener à des groupes d'électeurs proches votant de la même manière, même si individuellement ils auraient pu voter différemment.
- Pas d'influence des médias : La simulation suppose que chaque électeur possède une connaissance complète la position des candidats. Dans le vrai monde, les électeurs peuvent ne pas avoir à disposition toutes les informations dont ils auraient besoin pour voter, et tenter de faire au mieux en accord avec ce qu'ils savent. L'exposition aux médias et leur influence pourraient même dépendre de la position des électeurs.
- Pas de vote stratégique : Indépendamment de leur implémentation, beaucoup de méthodes de votes ont des défauts reconnus. Si vous êtes conscient de ces défauts, vous pourriez rationnellement trahir vos préférences, de telles sortes que l'un de vos candidats favoris ait plus de chance de remporter l'élection. Dans la simulation, chaque électeur est fidèle à ses préférences.
Note : Pour certains de ces défauts, vous pourriez avoir envie de considérer que les variables utilisées dans la simulation sont données par une régression logistique réalisée sur les vraies variables utilisées pour évaluer la position de chacun. Ceci implique qu'il faut évaluer les positions sur encore plus de variables, ce qui est incompatible avec le défaut évaluation omnisciente des positions. De plus, une régression logistique va induire au mieux une légère approximation, ce qui va accentuer le défaut représentation dimensionnelle.
Afin de mieux comprendre les résultats, vous pouvez lancer quelques fois la simulation et tenter de comprendre ce qu'il se passe entre les différents résultats des méthodes et l'ensemble des positions générées.
La première chose que l'on peut observer est que les résultats sont assez différents d'une méthode à l'autre. On peut voir que certaines méthodes donnent souvent des résultats similaires, ce qui peut ressembler à des correlations, mais la correspondance n'est pas systématique. Une analyse statistique est nécessaire pour établir de plus fortes corrélations. On peut remarquer que plusieurs de ces méthodes donne un vainqueur proche de la position moyenne des électeurs, pendant que d'autres favorisent les candidats sans trop d'autres adversaires dans leur zone.
S'il y a une seule question que vous devez retenir, c'est celle-ci :
Préféreriez-vous choisir comme vainqueur un candidat pour lequel personne n'était vraiment contre, ou un candidat qui possède plus de partisans que d'opposants, par rapport à ses concurrents ?
Interprétation personnelle : Dans ce paragraphe et dans le prochain, et uniquement dans ceux-ci, je donne mon opinion sur l'interprétation des résultats : je pense que les méthodes qui promeut des candidats isolés des autres ne sont pas les meilleures, car les résultats dépendent plus de la position des candidats que de celle des électeurs. Or, c'est bien la position de l'électorat que le vote est censé refléter. Dans ce sens, les meilleurs méthodes de vote sont, selon moi, celles qui permettent aux électeurs de juger les candidats indépendamment.
Dans un système qui favorise les candidats isolés, les candidats qui pourraient mieux représenter la position des électeurs doivent lutter les uns contre les autres, et c'est cette compétition qui permet aux candidats isolés de gagner.
Pour améliorer la simulation, la première chose à faire est d'ajouter d'autres méthodes de vote. Seulement sept ont été implémentées ici, mais de nombreuses autres existent, en plus de diverses variantes possibles, donnant des résultats différents.
Une fois que plus de méthodes de vote auront été implémentées, il serait bien de réaliser une étude statistique de corrélation entre les méthodes. L'idée serait de lancer la simulation un grand nombre de fois en stockant les résultats dans un fichier, puis d'estimer entre chaque paire de méthodes le taux d'accord, c'est-à-dire la fréquence à laquelle les méthodes donnent le même résultat.
Enfin, pour compléter cette analyse, d'autres variables telles que des indicateurs de distribution (médiane, moyenne et écart-type) et des indicateurs de densité (pour les électeurs et les candidats) pourraient aussi être utilisés pour trouuver des corrélations et être capable de conclure de manière rigoureuse sur le sujet des méthodes de vote.
Ce projet est un petit projet. Le code source est donné librement à la communauté GitHub, sous la seule licence MIT, qui n'est pas trop restrictive.