\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0maa\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0marray\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m2\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m2\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;32mprint\u001b[0m \u001b[0maa\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0minv\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mlinalg\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0minv\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0maa\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
+ "\u001b[0;32m/usr/local/lib/python2.7/site-packages/numpy/linalg/linalg.pyc\u001b[0m in \u001b[0;36minv\u001b[0;34m(a)\u001b[0m\n\u001b[1;32m 524\u001b[0m \u001b[0msignature\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m'D->D'\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0misComplexType\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mt\u001b[0m\u001b[0;34m)\u001b[0m \u001b[0;32melse\u001b[0m \u001b[0;34m'd->d'\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 525\u001b[0m \u001b[0mextobj\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mget_linalg_error_extobj\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0m_raise_linalgerror_singular\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 526\u001b[0;31m \u001b[0mainv\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0m_umath_linalg\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0minv\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0ma\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0msignature\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0msignature\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mextobj\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mextobj\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 527\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mwrap\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mainv\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mastype\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mresult_t\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcopy\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mFalse\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 528\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python2.7/site-packages/numpy/linalg/linalg.pyc\u001b[0m in \u001b[0;36m_raise_linalgerror_singular\u001b[0;34m(err, flag)\u001b[0m\n\u001b[1;32m 88\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 89\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0m_raise_linalgerror_singular\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0merr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mflag\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 90\u001b[0;31m \u001b[0;32mraise\u001b[0m \u001b[0mLinAlgError\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m\"Singular matrix\"\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 91\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 92\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0m_raise_linalgerror_nonposdef\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0merr\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mflag\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;31mLinAlgError\u001b[0m: Singular matrix"
+ ]
+ }
+ ],
+ "source": [
+ "aa = np.array([[1,2,3],[1,2,3],[3,3,3]])\n",
+ "print aa\n",
+ "inv = np.linalg.inv(aa)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[[ 2.]\n",
+ " [ 3.]\n",
+ " [-1.]]\n"
+ ]
+ }
+ ],
+ "source": [
+ "A = np.array([[2,1,-1],[-3,-1,2],[-2,1,2]])\n",
+ "B = np.array([[8],[-11],[-3]])\n",
+ "inv_A = np.linalg.inv(A)\n",
+ "print np.dot(inv_A,B)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[[ 2.]\n",
+ " [ 3.]\n",
+ " [-1.]]\n"
+ ]
+ }
+ ],
+ "source": [
+ "print np.linalg.solve(A,B)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial12 Modern Portfolio Theory.html b/Introduction to Financial Python/Tutorial12 Modern Portfolio Theory.html
new file mode 100644
index 0000000..b81bfbe
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial12 Modern Portfolio Theory.html
@@ -0,0 +1,98 @@
+Introduction
+In the past tutorials we introduced Python, statistics and linear algebra. From this chapter we are going to introduce theories in finance. We start fromModern Portfolio Theory, which contains risk-averse assumption, mean-variance analysis, asset allocation and portfolio optimization.
+Risk-averse Assumption
+
+We assume that all the investors are risk-averse, which means for every incremental risk, we ask for additional return on that. For example, if we have two asset A and B. A has 50% probability to pay $200 at the end of the year and 50% probability to pay 0. B has 50% probability to pay $400 at the end of the year and 50% probability to pay $-200(which mean ask for $200 from you). which one would you take?
+
+The expected return of A is
+\[E(A) = 0.5*200 + 0.5*0 = 100 \]
+And that for B is also
+\[E(B) = 0.5*400 + 0.5*(-200) = 100 \].
+While the standard deviation for A is
+\[\sigma_A = \sqrt{(0.5((200-100)^2 + (0-100)^2))} = 100 \] and that for B is
+\[\sigma_A = \sqrt{(0.5((400-100)^2 + (-200-100)^2))} = 300 \]
+Which asset would we choose?
+If you are an risk seeker, you may choose asset B, because you can potentially get a higher return.
+In modern portfolio theory, we assume that all the investors are risk-averse and rational. Under such assumption, all of the investor would prefer asset A and no one would choose asset B.
+Portfolio Variance
+Expected Return
+Let's consider two asset, A and B, with expected rate of return \(r_a\) and \(r_b\), and variance \(Var_a\) and \(Var_b\).
+If we buy A and B to construct a portfolio, what's the expected return and variance of the portfolio?
+The answer is that it depends on the weight of the two assets. If we have \(w_A\) on A and \(w_b\) on B, our expected return on the portfolio can be calculated by:
+\[E(p) = w_Ar_a + w_br_b\]
+Note that \(w_A + w_B\) must equal to 1 because they are the weight.
+Covariance and Correlation
+Before we move to portfolio variance, we need first to learn Covariance and Correlation.
+If asset A has a series of Daily return\((A_1,A_2,A_3...A_n)\), and asset B has a series of Daily return \((B_1,B_2,B_3...B_n)\), then the covariance of A and B is given by:
+\[Cov_{a,b} = \frac{1}{n}\sum_{i = 1}^{n}(A_i - \bar{A})(B_i - \bar{B})\]
+equivalently, we can also write it in the following form:
+Cov_{a,b} = E[(A-E[A])(B-E[B])]
+What's the economic intuition behind this? Let's image that if whenever A has a return higher than its mean return, B also has a return above its mean, the covariance would be a positive number. Otherwise if whenever A has a return above the mean, B has a return below the mean, the covariance would be a negative number. In other words, covariance is a measure of the joint variability of two random variable.
+However, different assets has different magnitude of variance. In order to compare them, we introduce the concept of correlation. We usually represent it by \(r\)
+\[r_{AB} = \frac{Cov_{AB}}{\sigma_A \sigma_B}\]
+Correlation takes value from the range [-1,1]. We would not prove it mathematically here, but you are encouraged to do so if you are interested in it.
+It worths mentioning that correlation value of both 1 and -1 mean linear relations. If random variable A and B have a 1 correlation, there must exist a \(\beta\) so that \(A = \beta B\), where \(\beta\) is a positive number. If the correlation is -1, \(\beta\) is a negative number.
+Two-asset Portfolio Variance
+Now let's consider Portfolio Variance. We have already learned the formula for variance, we can start from:
+\[Var[r_p] = E[(r_p - E[(r_p)])^2]\]
+\[= E[((w_Ar_A+w_Br_B)-(w_A\mu_A +w_B\mu_B))^2]\]
+\[= E[(w_A(r_A-\mu_A)+w_B(r_B-\mu_B))^2]\]
+\[= E[w_A^2(r_A - \mu_A)^2 + w_B^2(r_B-\mu_B)^2+2w_Aw_B(r_A-\mu_A)(r_B - \mu_B)]\]
+\[=w_A^2Var[r_A] + w^2Var[r_B] + 2w_Aw_BCov(r_A,r_B)\]
+Feel free to skip the middle process if you are not comfortable with math. You just need to remember the last term: The portfolio variance equals to the weight-square multiply the variance for each asset and them plus 2 times each weight times the covariance of the two assets.
+
+As we introduce the relationship between covariance and correlation, we can also write the above equation into:
+
+\[Var[r_p]=w_A^2Var[r_A] + w^2Var[r_B] + 2w_Aw_Br_{AB}\sigma_A\sigma_B\]
+
+From the equation, we can see that if the two stock have a very low or even negative correlation, the portfolio variance can be minimized. This is the so called Diversification.
+N-asset Portfolio Variance
+The formula to compute the Variance of an N-asset portfolio is much more complex, we need to use linear algebra to represent it. However, it follows the same rule as two-asset portfolio: if we add an asset that has low or negative correlation with others assets in this portfolio, the portfolio variance can be decreased.
+If we have N asset with \((r_1,r_2,r_3,...,r_n)\) expected rate of return, and the weight for each asset is \((he w_1,w_2,w_3,...,w_n)\), the portfolio variance can be calculated by:
+\[\sigma^2 = w^T\Sigma w\]
+Where
+\[\Sigma = \begin{pmatrix}
+Cov_{11}&Cov_{12}&Cov_{13}&...&Cov_{1n}\\
+Cov_{21}&Cov_{22}&Cov_{23}&...&Cov_{2n}\\
+Cov_{31}&Cov_{32}&Cov_{33}&...&Cov_{3n}\\
+...&...&...&...&...\\
+Cov_{n1}&Cov_{n2}&Cov_{n3}&...&Cov_{nn}
+\end{pmatrix}\]
+To calculate the variance, we are doing matrix multiplication \(1\times n \times n \times n \times n \times 1 = 1 \times 1\). That's why we ends up with a number, which is our portfolio variance.
+Mean-Variance Analysis
+Is the portfolio with the lowest standard deviation the portfolio we are seeking? The answer is no. Don't forget we have risk-free rate, which has zero variance(of course there is no absolute risk-free asset, but we usually consider U.S. treasure as risk-free).
+
+Because of risk-free, we will not hold any risky portfolio that has a expected return lower than the risk-free. It worths noting that we say 'risky portfolio' here instead of 'risky asset' because we can possible hold an risky asset in our portfolio if this asset has negative correlation with other asset in our portfolio.
+
+there are infinite kinds of possible portfolio combination, but you can't diversify all of the portfolio risk away. In other words, you can't construct a portfolio with zero standard deviation with any combination of risky asset, otherwise there would be arbitrage opportunity.
+
+If we plot all the assets and all the portfolio on a chart, with standard deviation on the horizontal axis and expected return on the vertical axis, we will get a chart below: +We simulated this graph using 10 stocks. In the real world there are far more than 10 assets, but the graph would be almost the same shape. Before demonstrating how to simulate this, we should totally understand it.
+
+The black curve is called efficient frontier. More accurately speaking, only the part above the blue dash-line is. Efficient frontier means that for a given expected return, you can't achieve a standard deviation lower than that of the portfolio on the efficient frontier. In other words, all of the assets and possible portfolio should lie inside the efficient frontier.
+
+Start from the definition of efficient frontier, we know that for any given standard deviation, the portfolio on the efficient frontier has a higher return, so we would only choose the portfolio on the efficient frontier. However, we have infinite number of portfolios on the efficient frontier, which one should we choose? Now we need to understand the concept of Sharpe Ratio.
+
+We simulated this graph using 10 stocks. In the real world there are far more than 10 assets, but the graph would be almost the same shape. Before demonstrating how to simulate this, we should totally understand it.
+
+The black curve is called efficient frontier. More accurately speaking, only the part above the blue dash-line is. Efficient frontier means that for a given expected return, you can't achieve a standard deviation lower than that of the portfolio on the efficient frontier. In other words, all of the assets and possible portfolio should lie inside the efficient frontier.
+
+Start from the definition of efficient frontier, we know that for any given standard deviation, the portfolio on the efficient frontier has a higher return, so we would only choose the portfolio on the efficient frontier. However, we have infinite number of portfolios on the efficient frontier, which one should we choose? Now we need to understand the concept of Sharpe Ratio.
+Sharpe Ratio
+Sharpe Ratio is defined by:
+\[SR = \frac{r_i - rf}{\sigma_i}\]
+The economical intuition behind Sharpe ratio is that given a small incremental risk, how much return excess the risk-free can I get. Of course everyone want a higher return on a small incremental, thus sharpe ratio is the standard for us to find the optimized portfolio.
+
+In this chart, the sharpe ratio of each asset is exactly the slope of the straight line across the asset and the risk-free rate. Starting from the risk-free rate point, we find the tangent line of the efficient frontier. This is why the optimized portfolio is also called 'tangent portfolio'.
+
+From the formula calculating the portfolio variance, we know that adding more stocks with negative correlation will decrease the risk. However, we are not looking for the portfolio with lowest variance, but the portfolio with highest sharpe ratio.
+ +The blue curve in the chart above is the efficient frontier formed by the portfolios with only three stocks: IBM, GE, and PFE. Obviously the portfolios on this curve has lower sharpe ratio than the portfolios on the original efficient frontier. As the number of stocks increases, the efficient frontier becomes better.
+
+The blue curve in the chart above is the efficient frontier formed by the portfolios with only three stocks: IBM, GE, and PFE. Obviously the portfolios on this curve has lower sharpe ratio than the portfolios on the original efficient frontier. As the number of stocks increases, the efficient frontier becomes better.
+Capital Market Line
+The basic assumption of modern portfolio theory is that all of the investors are rational, which means all of they are smart enough to construct the optimized portfolio, or market portfolio. Under this assumption, all of the investors should hold the same proportion of risky assets. Since the investors are rational, they will only hold the portfolios on the red line above, which is called Capital Market Line. The reason is straightforward: all the portfolios on the capital market line has the same sharpe ratio, and this is the highest sharpe ratio this world can achieve.
+
+The way to construct a portfolio on the capital market line is to hold risk-free asset and the market portfolio. Remember the variance for two-asset portfolio:
+\[\sigma^2 =w_A^2Var[r_A] + w^2Var[r_B] + 2w_Aw_BCov(r_A,r_B)\]
+If A is the market portfolio and B is risk-free asset, since both the variance of risk-free and the covariance of risk-free with any other asset is zero, the formula becomes:
+\[\sigma_p =w_A\sigma_A \]
+This formula tells us that the portfolio standard deviation has linear relation with the weight of market portfolio. In other words, if I put 50% weight in the risk-free asset and 50% weight in the market portfolio, my portfolio will lie on the center of the capital market line.
+
+Under the rational assumption, if my portfolio is difference with yours, the reason must be that we put different weight in the risk-free asset and market portfolio. However, we hold the same market portfolio, which means the proportion of the risky asset in the market portfolio are the same. It's very important to make this clear.
+
+What if I extend the the market capital line to achieve a higher return at a higher risk? There is another import assumption that there is no transaction cost, which means I can borrow money as much as I wish. In order to achieve a higher return, we need to borrow risk-free asset, or short risk-free, and invest the proceeds together with our own money to the market portfolio. Under such circumstance, our weight on risk-free is negative, and the weight on the market portfolio is larger than 1.
+Summary
+In this chapter we learned modern portfolio theory. It's important to understand here is that by holding difference stocks we can achieve a portfolio with higher sharpe ratio, and all the investors holds the same amount of risky asset, which is the market portfolio. In the next chapter we will introduce asset pricing with CAPM, which is the most classical asset pricing model.
diff --git a/Introduction to Financial Python/Tutorial2 Logical Operation and Loop.html b/Introduction to Financial Python/Tutorial2 Logical Operations and Loops.html
similarity index 100%
rename from Introduction to Financial Python/Tutorial2 Logical Operation and Loop.html
rename to Introduction to Financial Python/Tutorial2 Logical Operations and Loops.html
diff --git a/Introduction to Financial Python/Tutorial2 Logical Operation and Loop.ipynb b/Introduction to Financial Python/Tutorial2 Logical Operations and Loops.ipynb
similarity index 100%
rename from Introduction to Financial Python/Tutorial2 Logical Operation and Loop.ipynb
rename to Introduction to Financial Python/Tutorial2 Logical Operations and Loops.ipynb
diff --git a/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.html b/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.html
new file mode 100644
index 0000000..4097816
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.html
@@ -0,0 +1,112 @@
+Introduction
+In the last tutorial we introduced logical operations, for/while loop and list comprehension. We will introduce functions and objective-oriented programming in this chapter, which will enable us to build complex algorithms in more flexible ways.
+Functions
+A function is a reusable block of code. You can use a function to make a calculation, output a value, or do anything else you want. We can easily define our own function by using the keyword 'def'.
+def product(x,y):
+ return x*y
+product(2,3)
+product(5,10)
+
+The keyword 'def' is followed by the function name and the parenthesized list of formal parameters. The statements that form the body of the function start at the next line, and must be indented. Here the 'x' and 'y' are the two parameters. A function doesn't necessarily have parameters.
+def say_hi():
+ print 'Welcome to QuantConnect'
+say_hi()
+
+Built-in Function
+Here we introduce some commonly used Python built-in functions.
+range() is a function to create lists containing arithmetic progressions. It's often used in for loops. the arguments must be integers. If the step argument is omitted, it defaults to 1.
+range(10)
+range(1,11)
+range(1,11,2)
+
+Another useful function usually used together with range() to create a for loop is len(). This function returns the length of an object. The argument must be a sequence or a collection.
+tickers = ['AAPL','GOOG','IBM','FB','F','V', 'G', 'GE']
+print 'The length of tickers is {}'.format(len(tickers))
+for i in range(len(tickers)):
+ print tickers[i]
+
+map() is a function that applies a specific function to every item of a sequence or collection, and returns a list of the results.
+tickers = ['AAPL','GOOG','IBM','FB','F','V', 'G', 'GE']
+print map(len,tickers)
+
+The Lambda operator is a way to create small anonymous functions. These functions are throw-away functions, which means they are just needed where they have been created.For example:
+map(lambda x: x**2, range(10))
+
+map() can be applied to more than one list. The lists have to have the same length.
+map(lambda x, y: x+y, [1,2,3,4,5],[5,4,3,2,1])
+
+sort() returns a new sorted list from the items in a sequence or a collection.
+sorted([5,2,3,4,1])
+
+We can add a 'key' parameter to specify a function to be called on each list element prior to making comparisons. For example:
+price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]
+sorted(price_list, key = lambda x: x[1])
+
+By default the values are sorted by ascending order. We can change it to descending by adding an optional parameter 'reverse'.
+price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]
+sorted(price_list, key = lambda x: x[1],reverse = True)
+
+A list object also has a function list.sort(). This function takes the same 'key' and 'reverse' arguments as sorted, but we don't need to specify the sequence to be sorted.
+price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]
+price_list.sort(key = lambda x: x[1])
+print price_list
+
+Objective-oriented Programming
+Python is an objective-oriented programming language. It's important to understand the concept of 'Object' because almost every kind of data from QuantConnect API is an object.
+Class
+a class is a kind of data type, just like a string, float, or list. When we create an object of that data type, we call it an instance of a class.
+In python, everything is an object - everything is an instance of some class. The data values which we store inside an object are called properties, and the functions which are associated with the object are called methods. For example, as we mentioned above, a list is an object of 'list' class, and it has a method list.sort().
+We can create our own objects by defining a certain class. We would do this when it's helpful to group certain functions together.
+For example, we defined a class named stock here:
+class stock:
+ def __init__(self, ticker, open, close, volume):
+ self.ticker = ticker
+ self.open = open
+ self.close = close
+ self.volume = volume
+ self.rate_return = float(close)/open - 1
+
+ def update(self, open, close):
+ self.open = open
+ self.close = close
+ self.rate_return = float(self.close)/self.open - 1
+
+ def print_return(self):
+ print self.rate_return
+
+Here we defined a class named 'stock'. it has attributes 'ticker', 'open', 'close', 'volume' and 'rate_return'. Inside the class body, the first method is called __init__, which is a special method. When we create a new instance of the class, the __init__ method is immediately executed with all the parameters that we passed to the class object. The purpose of this method is thus to set up a new object using data that we have provided.
+This class also has methods 'update' and 'print_return'. Now we are going to create two stock objects,'apple' and 'google'.
+apple = stock('AAPL', 143.69, 144.09, 20109375)
+google = stock('GOOG', 898.7, 911.7, 1561616)
+
+Now we can access to the properties and call the functions associated with the stock class.
+apple.ticker
+google.print_return()
+google.update(912.8,913.4)
+google.print_return()
+
+By calling the stock.update() function, we updated the open and close price of the stock. Please notice that when we use the properties or call the methods inside a method, we need to specify them as self.property or self.method(), otherwise Python will deem them as global variables thus cause error.
+We can easily assign add a property to an object anywhere.
+apple.ceo = 'Tim Cook'
+apple.ceo
+
+We can check what properties are defined on an object using the dir() function:
+dir(apple)
+
+Inheritance
+Inheritance is a way of arranging objects in a hierarchy from the most general to the most specific. An object which inherits from another object is considered to be a subtype of that object. The subtype will inherit the methods. For example, we define a class named 'child', and it inherits 'stock':
+class child(stock):
+ def __init__(self,name):
+ self.name = name
+
+Then we create an object:
+aa = child('aa')
+aa.name
+aa.update(100,102)
+aa.open
+aa.close
+aa.print_return()
+
+As we can see above, the new class child inherited the methods from stock.
+Summary
+In this chapter we introduced functions and class. When we write a QC algorithm, we would define our algorithm as a class(QCAlgorithm). This means our algorithm inherited the QC API methods from QCAlgorithm class. It's essential to understand class and inheritance so that we can understand how a QC algorithm works. This is the last chapter of basic python part. In the next chapter we will introduce NumPy and a little bit Pandas, which enable us to conduct scientific calculation with Python.
diff --git a/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.ipynb b/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.ipynb
new file mode 100644
index 0000000..72756de
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial3 Functions and Objective-oriented Programming.ipynb
@@ -0,0 +1,409 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "50"
+ ]
+ },
+ "execution_count": 1,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "def product(x,y):\n",
+ " return x*y\n",
+ "product(2,3)\n",
+ "product(5,10)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Welcome to QuantConnect\n"
+ ]
+ }
+ ],
+ "source": [
+ "def say_hi():\n",
+ " print 'Welcome to QuantConnect'\n",
+ "say_hi()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[1, 3, 5, 7, 9]"
+ ]
+ },
+ "execution_count": 3,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "range(10)\n",
+ "range(1,11)\n",
+ "range(1,11,2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "The length of tickers is 8\n",
+ "AAPL\n",
+ "GOOG\n",
+ "IBM\n",
+ "FB\n",
+ "F\n",
+ "V\n",
+ "G\n",
+ "GE\n"
+ ]
+ }
+ ],
+ "source": [
+ "tickers = ['AAPL','GOOG','IBM','FB','F','V', 'G', 'GE']\n",
+ "print 'The length of tickers is {}'.format(len(tickers))\n",
+ "for i in range(len(tickers)):\n",
+ " print tickers[i]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[4, 4, 3, 2, 1, 1, 1, 2]\n"
+ ]
+ }
+ ],
+ "source": [
+ "tickers = ['AAPL','GOOG','IBM','FB','F','V', 'G', 'GE']\n",
+ "print map(len,tickers)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "map(lambda x: x**2, range(10))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[6, 6, 6, 6, 6]"
+ ]
+ },
+ "execution_count": 9,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "map(lambda x, y: x+y, [1,2,3,4,5],[5,4,3,2,1]) "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[1, 2, 3, 4, 5]"
+ ]
+ },
+ "execution_count": 10,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "sorted([5,2,3,4,1])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[('MSFT', 69), ('WMT', 75.32), ('AAPL', 144.09), ('FB', 150), ('GOOG', 911.71)]"
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]\n",
+ "sorted(price_list, key = lambda x: x[1])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[('GOOG', 911.71), ('FB', 150), ('AAPL', 144.09), ('WMT', 75.32), ('MSFT', 69)]"
+ ]
+ },
+ "execution_count": 12,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]\n",
+ "sorted(price_list, key = lambda x: x[1],reverse = True)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[('MSFT', 69), ('WMT', 75.32), ('AAPL', 144.09), ('FB', 150), ('GOOG', 911.71)]\n"
+ ]
+ }
+ ],
+ "source": [
+ "price_list = [('AAPL',144.09),('GOOG',911.71),('MSFT',69),('FB',150),('WMT',75.32)]\n",
+ "price_list.sort(key = lambda x: x[1])\n",
+ "print price_list"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "class stock:\n",
+ " def __init__(self, ticker, open, close, volume):\n",
+ " self.ticker = ticker\n",
+ " self.open = open\n",
+ " self.close = close\n",
+ " self.volume = volume\n",
+ " self.rate_return = float(close)/open - 1\n",
+ " \n",
+ " def update(self, open, close):\n",
+ " self.open = open\n",
+ " self.close = close\n",
+ " self.rate_return = float(self.close)/self.open - 1\n",
+ " \n",
+ " def print_return(self):\n",
+ " print self.rate_return"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "apple = stock('AAPL', 143.69, 144.09, 20109375)\n",
+ "google = stock('GOOG', 898.7, 911.7, 1561616)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.0144653388227\n",
+ "0.000657318141981\n"
+ ]
+ }
+ ],
+ "source": [
+ "apple.ticker\n",
+ "google.print_return()\n",
+ "google.update(912.8,913.4)\n",
+ "google.print_return()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "'Tim Cook'"
+ ]
+ },
+ "execution_count": 17,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "apple.ceo = 'Tim Cook'\n",
+ "apple.ceo"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "['__doc__',\n",
+ " '__init__',\n",
+ " '__module__',\n",
+ " 'ceo',\n",
+ " 'close',\n",
+ " 'open',\n",
+ " 'print_return',\n",
+ " 'rate_return',\n",
+ " 'ticker',\n",
+ " 'update',\n",
+ " 'volume']"
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "dir(apple)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "class child(stock):\n",
+ " def __init__(self,name):\n",
+ " self.name = name"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.02\n"
+ ]
+ }
+ ],
+ "source": [
+ "aa = child('aa')\n",
+ "aa.name\n",
+ "aa.update(100,102)\n",
+ "aa.open\n",
+ "aa.close\n",
+ "aa.print_return()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.html b/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.html
new file mode 100644
index 0000000..699d459
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.html
@@ -0,0 +1,105 @@
+Introduction
+We have already introduced basic python part. Now let's take a look at NumPy and Pandas, which allow us to do something with math and data.
+
+NumPy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these array. It also has strong integration with Pandas, which is another power tool for manipulating financial data.
+
+We introduced the concept of class in the last chapter. A python package is essentially a executable python script and we use the class and methods in the package by importing the script.
+import numpy as np
+
+
+NumPy
+Basic NumPy Arrays
+A NumPy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. Here we make an array by passing a list of Apple stock price:
+price_list = [143.73, 145.83, 143.68, 144.02, 143.5, 142.62]
+price_array = np.array(price_list)
+print price_array, type(price_array)
+
+Notice that the type of array is 'ndarray'. This means it's a multiple-dimensional array. If we pass np.array() a list of lists, it will create a 2-dimensional array.
+Ar = np.array([[1,3],[2,4]])
+print Ar, type(Ar)
+
+We can access the dimensions of an array using the array.shape property:
+print Ar.shape
+
+If we create an 2-dimensional array, we call it a matrix, and each list is an vector. We can access to the list by index:
+print Ar[0]
+print Ar[1]
+
+If we want to access to the matrix by column:
+print 'the first column: ', Ar[:,0]
+print 'the second column: ', Ar[:,1]
+
+Array Functions
+There are some very useful functions built in NumPy allow us to make calculations on an array or array elements.
+print np.log(price_array)
+
+This function apply logarithm to each element and return an array.
+Some functions return a single value:
+print np.mean(price_array)
+print np.std(price_array)
+print np.sum(price_array)
+print np.max(price_array)
+
+The above functions return the mean, standard deviation(we will introduce these concepts in the following tutorials) and the max value of the array.
+Pandas Basic
+Pandas is probably the most powerful tools for dealing with financial data. Here we start from the basic Pandas data structure.
+import pandas as pd
+
+Series
+Series is a one-dimensional labeled array capable of holding any data type(integers, strings, float, python object, etc.) The axis labels are collectively refer to as the 'index'. The basic method to create a Series is to call Pandas.Series(data,index = index), where data can be a dictionary, an array or just a scalar value.
+price = [143.73, 145.83, 143.68, 144.02, 143.5, 142.62]
+s = pd.Series(price)
+print s
+
+We can create our customized index while creating the series:
+s = pd.Series(price,index = ['a','b','c','d','e','f'])
+print s
+
+We can easily set or change the index of an existing arrar:
+s.index = [6,5,4,3,2,1]
+print s
+
+Series is like a list in that we can slice it by index:
+print s[1:]
+print s[:-2]
+
+Series is also like a fixed-size dictionary in that we can get and set values by index label:
+print s[4]
+s[4] = 0
+print s
+
+Series can also have a name attribute, which will be used when we make up a Pandas DataFrame using several series.
+s = pd.Series(price, name = 'Apple Price List')
+print s
+print s.name
+
+Time Index
+pandas has a built-in function specifically for creating date indices, Pandas.date_range(). We use the function here to create a new index for our series:
+time_index = pd.date_range('2017-01-01',periods = len(s),freq = 'D')
+print time_index
+s.index = time_index
+print s
+
+Series are usually accessed using the iloc[] and loc[] methods. iloc[] is used to access elements by integer index, and loc[] is used to access the index of the series.
+iloc[] is necessary when the index of a series are integers, take our previous defined series as example:
+s.index = [6,5,4,3,2,1]
+print s
+print s[1]
+
+If we intended to take the second element of the series, we would make a mistake here, because the index are integers. In order to access to the element we want, we use iloc[] here:
+print s.iloc[1]
+
+While working with time-series financial data, we often use time as index. Pandas provide us a variety of methods to access the data by time index.
+s.index = time_index
+print s['2017-01-03']
+
+We can even access to a range of dates:
+print s['2017-01-02':'2017-01-05']
+
+Series[] provides us a very flexible way to index data. We can add any condition in the square brackets:
+print s[s < np.mean(s)]
+print s[(s > np.mean(s)) & (s < np.mean(s) + 1.64*np.std(s))]
+
+As demonstrated, we can use logical operators &, |, and ~(and, or, and not, respectively) to group multiple conditions.
+Summary
+Here we introduced NumPy, and basic part of Pandas. Now we are able to do some scientific computing with Python. In the next chapter we will dive into Pandas to learn resampling and manipulating Pandas DataFrame, which is the most commonly used method to do financial data analysis.
diff --git a/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.ipynb b/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.ipynb
new file mode 100644
index 0000000..2119ec7
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial4 NumPy and Basic Pandas.ipynb
@@ -0,0 +1,477 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "import numpy as np"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[ 143.73 145.83 143.68 144.02 143.5 142.62] \n"
+ ]
+ }
+ ],
+ "source": [
+ "price_list = [143.73, 145.83, 143.68, 144.02, 143.5, 142.62]\n",
+ "price_array = np.array(price_list)\n",
+ "print price_array, type(price_array)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[[1 3]\n",
+ " [2 4]] \n"
+ ]
+ }
+ ],
+ "source": [
+ "Ar = np.array([[1,3],[2,4]])\n",
+ "print Ar, type(Ar)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "(2, 2)\n"
+ ]
+ }
+ ],
+ "source": [
+ "print Ar.shape"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[1 3]\n",
+ "[2 4]\n"
+ ]
+ }
+ ],
+ "source": [
+ "print Ar[0]\n",
+ "print Ar[1]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "the first column: [1 2]\n",
+ "the second column: [3 4]\n"
+ ]
+ }
+ ],
+ "source": [
+ "print 'the first column: ', Ar[:,0]\n",
+ "print 'the second column: ', Ar[:,1]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[ 4.96793654 4.98244156 4.9675886 4.96995218 4.96633504 4.96018375]\n"
+ ]
+ }
+ ],
+ "source": [
+ "print np.log(price_array) "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "143.896666667\n",
+ "0.967379047852\n",
+ "863.38\n",
+ "145.83\n"
+ ]
+ }
+ ],
+ "source": [
+ "print np.mean(price_array)\n",
+ "print np.std(price_array)\n",
+ "print np.sum(price_array)\n",
+ "print np.max(price_array)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "import pandas as pd"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0 143.73\n",
+ "1 145.83\n",
+ "2 143.68\n",
+ "3 144.02\n",
+ "4 143.50\n",
+ "5 142.62\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "price = [143.73, 145.83, 143.68, 144.02, 143.5, 142.62]\n",
+ "s = pd.Series(price)\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "a 143.73\n",
+ "b 145.83\n",
+ "c 143.68\n",
+ "d 144.02\n",
+ "e 143.50\n",
+ "f 142.62\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "s = pd.Series(price,index = ['a','b','c','d','e','f'])\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "6 143.73\n",
+ "5 145.83\n",
+ "4 143.68\n",
+ "3 144.02\n",
+ "2 143.50\n",
+ "1 142.62\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "s.index = [6,5,4,3,2,1]\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "5 145.83\n",
+ "4 143.68\n",
+ "3 144.02\n",
+ "2 143.50\n",
+ "1 142.62\n",
+ "dtype: float64\n",
+ "6 143.73\n",
+ "5 145.83\n",
+ "4 143.68\n",
+ "3 144.02\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print s[1:]\n",
+ "print s[:-2]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "143.68\n",
+ "6 143.73\n",
+ "5 145.83\n",
+ "4 0.00\n",
+ "3 144.02\n",
+ "2 143.50\n",
+ "1 142.62\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print s[4]\n",
+ "s[4] = 0\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0 143.73\n",
+ "1 145.83\n",
+ "2 143.68\n",
+ "3 144.02\n",
+ "4 143.50\n",
+ "5 142.62\n",
+ "Name: Apple Price List, dtype: float64\n",
+ "Apple Price List\n"
+ ]
+ }
+ ],
+ "source": [
+ "s = pd.Series(price, name = 'Apple Price List')\n",
+ "print s\n",
+ "print s.name"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "DatetimeIndex(['2017-01-01', '2017-01-02', '2017-01-03', '2017-01-04',\n",
+ " '2017-01-05', '2017-01-06'],\n",
+ " dtype='datetime64[ns]', freq='D')\n",
+ "2017-01-01 143.73\n",
+ "2017-01-02 145.83\n",
+ "2017-01-03 143.68\n",
+ "2017-01-04 144.02\n",
+ "2017-01-05 143.50\n",
+ "2017-01-06 142.62\n",
+ "Freq: D, Name: Apple Price List, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "time_index = pd.date_range('2017-01-01',periods = len(s),freq = 'D')\n",
+ "print time_index\n",
+ "s.index = time_index\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "6 143.73\n",
+ "5 145.83\n",
+ "4 143.68\n",
+ "3 144.02\n",
+ "2 143.50\n",
+ "1 142.62\n",
+ "Name: Apple Price List, dtype: float64\n",
+ "142.62\n"
+ ]
+ }
+ ],
+ "source": [
+ "s.index = [6,5,4,3,2,1]\n",
+ "print s\n",
+ "print s[1]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "145.83\n"
+ ]
+ }
+ ],
+ "source": [
+ "print s.iloc[1]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "143.68\n"
+ ]
+ }
+ ],
+ "source": [
+ "s.index = time_index\n",
+ "print s['2017-01-03']"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "2017-01-02 145.83\n",
+ "2017-01-03 143.68\n",
+ "2017-01-04 144.02\n",
+ "2017-01-05 143.50\n",
+ "Freq: D, Name: Apple Price List, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print s['2017-01-02':'2017-01-05']"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "2017-01-01 143.73\n",
+ "2017-01-03 143.68\n",
+ "2017-01-05 143.50\n",
+ "2017-01-06 142.62\n",
+ "Name: Apple Price List, dtype: float64\n",
+ "2017-01-04 144.02\n",
+ "Freq: D, Name: Apple Price List, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print s[s < np.mean(s)] \n",
+ "print s[(s > np.mean(s)) & (s < np.mean(s) + 1.64*np.std(s))]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.html b/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.html
new file mode 100644
index 0000000..ae5b186
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.html
@@ -0,0 +1,178 @@
+Introduction
+In the last chapter we had a glimpse of Pandas. In this chapter we will learn resampling methods and DataFrame manipulating with real financial data. DataFrame is a very powerful tool for data analysis, and we will cover some commonly used methods dealing with financial data.
+
+Here we use the data from yahoo_finance API.
+import quandl
+quandl.ApiConfig.api_key = 'dRQxJ15_2nrLznxr1Nn4'
+aapl_table = quandl.get('WIKI/AAPL')
+aapl = aapl_table['Adj. Close']['2017']
+
+Resampling
+Last time we discussed how to access to series data by date index. Let's start from here using real financial time series data. aapl is a series who's values are Apple stock's daily close price, and the index is date. We will introduce how to obtain this series later.
+print aapl
+
+We have already known that we can access to a specific data point using series['yyyy-mm-dd']. We can also get access to the data in a specific month by simply using series['yyyy-mm'].
+print aapl['2017-3']
+
+Or in some consecutive months:
+aapl['2017-2':'2017-4']
+
+seires.head() and series.tail() are also useful method to quickly get access to the first or last N elements.
+print aapl.head(5)
+print aapl.tail(10)
+
+Now we introduce a very powerful method: resample(). series.resample(freq) is a class called 'resampler'. The Argument freq tells the resampler the frequency for aggregating data. series.resample.mean() is a complete statement that aggregate the data by mean by a certain frequency. For example, if we want to aggregate the daily data into monthly data by mean:
+by_month = aapl.resample('M').mean()
+print by_month
+
+We can also aggregate the data by week:
+by_week = aapl.resample('W').mean()
+print by_week
+
+Virtually we can use almost any frequency we want by simply use the format 'nf', where 'n' is an integer and 'f' is M for month, W for week and D for day.
+three_day = aapl.resample('3D').mean()
+two_week = aapl.resample('2W').mean()
+two_month = aapl.resample('2M').mean()
+
+We can also change the aggregating method. By default we can use mean(), std(), max(), min(), which are mean, standard deviation, maximum value and minimum value respectively.
+std = aapl.resample('W').std()
+max = aapl.resample('W').max()
+min = aapl.resample('W').min()
+
+However, most of the time we don't want to aggregate in these methods. For example, if we want to calculate monthly return of the stock, we may just want to access the data for the last day of a month. Fortunately, we can customize the aggregating method. We write our function in series.resample.agg().
+last_day = aapl.resample('M').agg(lambda x: x[-1])
+print last_day
+
+Or directly calculate the monthly rates of return using the data for the first day and the last day:
+monthly_return = aapl.resample('M').agg(lambda x: x[-1]/x[1] - 1)
+print monthly_return
+
+Series object also provides us some convenient methods to do some quick calculation.
+print monthly_return.mean()
+print monthly_return.std()
+print monthly_return.max()
+
+We can also check the statistical summaries of a series.
+print aapl.describe()
+
+Another two frequently used method is series.diff() and series.pct_change(). This first method calculates the different between consecutive elements, and the second one calculates the percentage changes.
+print last_day.diff()
+print last_day.pct_change()
+
+You may noticed that we induced a NaN value while calculating the percentage change, or rate or return.
+When dealing with NaN, we usually either removing the data point or fill it with a specific value. Here we fill it with value 0:
+daily_return = last_day.pct_change()
+print daily_return.fillna(0)
+
+We fill it with the next fitted value. This is called 'backward fill', or 'bfill' in short:
+daily_return = last_day.pct_change()
+print daily_return.fillna(method = 'bfill')
+
+As you expected, since there is a 'backward fill' method, there must be a 'forward fill' method, or 'ffill' in short. However we can't use it here because the NaN is the first value.
+We can also simply remove the NaN data point by series.dropna().
+daily_return = last_day.pct_change().dropna()
+print daily_return
+
+DataFrame
+After the long introduction to Series, finally we are going to discuss the most commonly used Pandas data structure: Pandas DataFrame. A DataFrame is essentially a group of series, thus it's not hard to understand how a DataFrames works if we master the series.
+
+DataFrame is a 2-dimensional labeled data structure with columns of potentially different types. You can think it like a spreadsheet or SQL table. Like series, DataFrame accepts many different kinds of input: dictionary, 2-D numpy.ndarray, a series and other DataFrame.
+Create DataFrames
+The most commonly used method to create a DataFrame is passing a data dictionary.
+dict = {'AAPL': [143.5, 144.09, 142.73, 144.18, 143.77],'GOOG':[898.7, 911.71, 906.69, 918.59, 926.99],
+ 'IBM':[155.58, 153.67, 152.36, 152.94, 153.49]}
+data_index = pd.date_range('2017-07-03',periods = 5, freq = 'D')
+df = pd.DataFrame(dict, index = data_index)
+print df
+
+Manipulating DataFrames
+We can access to the values in a DataFrame by columns and index. Each columns in a DataFrame is essentially a pandas series. We can access to a column by square brackets df['column_name']. The columns names are also properties of the DataFrame, so we can also use df.column_name to get the columns. In the previous demonstration, we used exactly this method to access to the Apple stock close price series.
+df = aapl_table
+print df.Close.tail(5)
+print df['Adj. Volume'].tail(5)
+
+All the methods we apply to a series index such as iloc[], loc[], and resampling methods, can also be applied to a DataFrame:
+aapl_2016 = df['2016']
+aapl_month = aapl_2016.resample('M').agg(lambda x: x[-1])
+print aapl_month
+
+It's easy to access to multiple columns to form a subset of the original DataFrame:
+aapl_bar = aapl_month[['Open', 'High', 'Low', Close']]
+print aapl_bar
+
+We can also combined the methods above using loc[ ]. We separate the index and columns by comma to specify the range of data we want:
+print aapl_month.loc['2016-03':'2016-06',['Open', 'High', 'Low', 'Close']]
+
+The subset methods in DataFrame is very powerful. By writing logical statements in square brackets, we can make customized subsets:
+above = aapl_bar[aapl_bar.Close > np.mean(aapl_bar.Close)]
+print above
+Data Validation
+As we mentioned, all the series methods can be apply to a DataFrame in the same way. Here we create a new column from an existing DataFrame:
+aapl_bar['rate_return'] = aapl_bar.Close.pct_change()
+print aapl_bar
+
+Here the calculation introduced a NaN value. If the DataFrame is large, we would not be able to observe it. isnull() provides a convenient way to check abnormal values.
+missing = aapl_bar.isnull()
+print missing
+print '------------------ separate line ------------'
+print missing.describe()
+
+Note that the only column with value 2 in row 'unique' is 'rate_return'. This indicate that there are at least one missing value in the column 'rate_return'. We can even know the number of missing values by comparing 'count' and 'freq'. There are 12 counts and 11 'False', we know there is one 'True', which is the missing value.
+We can also find the rows with missing values easily:
+print missing[missing.rate_return == True]
+
+Usually when dealing with missing data, we either delete the whole row or fill it with some value. As we introduced in the series chapter, the same method df.dropna() and df.fillna() can be applied to a DataFrame.
+drop = aapl_bar.dropna()
+print drop
+print '---------------------- separate ----------------------'
+fill = aapl_bar.fillna(0)
+print fill
+
+DataFrame Concat
+We have already known how to extract a series from a dataFrame. Now we need to consider how to merge a series or a DataFrame into another one.
+In Pandas, the function concat handles almost all of the merge tasks.
+We can merge multiple series into a DataFrame:
+s1 = pd.Series([143.5, 144.09, 142.73, 144.18, 143.77], name = 'AAPL')
+s2 = pd.Series([898.7, 911.71, 906.69, 918.59, 926.99], name = 'GOOG')
+data_frame = pd.concat([s1,s2], axis = 1)
+print data_frame
+
+joining two DataFrames by axis:
+log_price = np.log(aapl_bar.Close)
+log_price.name = 'log_price'
+print log_price
+print '\n---------------------- separate line--------------------\n'
+concat = pd.concat([aapl_bar, log_price], axis = 1)
+print concat
+When we joining a DataFrame into another, we can indicate whether we want to merge by index.
+df_volume = aapl_table.loc['2016-10':'2017-04',['Volume', 'Split Ratio']].resample('M').agg(lambda x: x[-1])
+print df_volume
+print '\n---------------------- separate line--------------------\n'
+df_2017 = aapl_table.loc['2016-10':'2017-04',['Open', 'High', 'Low', 'Close']].resample('M').agg(lambda x: x[-1])
+print df_2017
+
+Using the methods we have already learned, we subset two DataFrames from the original one. Now we are going to merge the them with our DataFrame 'aapl_bar'
+concat = pd.concat([aapl_bar,df_volume],axis = 1)
+print concat
+
+By default the the DataFrame are joined with all of the data. This default options results in zero information loss. We can also merge them by intersection, this is called 'inner join':
+concat = pd.concat([aapl_bar,df_volume],axis = 1, join = 'inner')
+print concat
+
+Only the intersection part was left if use 'inner join' method.
+Now let's try to append a DataFrame to another one:
+append = aapl_bar.append(df_2017)
+print append
+
+'Append' is essentially to concat two DataFrames by axis = 0, thus here is an alternative way to append:
+concat = pd.concat([aapl_bar, df_2017], axis = 0)
+print concat
+
+Please note that if the two DataFrame have some columns with the same column names, these columns are considered to be the same and will be merged. It's very important to have the right column names. If we change a column names here:
+df_2017.columns = ['Change', 'High','Low','Close']
+concat = pd.concat([aapl_bar, df_2017], axis = 0)
+print concat
+
+Since the column name of 'Open' has been changed, the new DataFrame has an new column named 'Change'.
+Summary
+Hereby we introduced the most import part of python: resampling and DataFrame manipulation. We only introduced the most commonly used method in Financial data analysis. There are also many methods used in data mining, which are also beneficial. You can always check the Pandas official documentations for help.
diff --git a/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.ipynb b/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.ipynb
new file mode 100644
index 0000000..0d964b2
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial5 Pandas-Resampling and DataFrame.ipynb
@@ -0,0 +1,1079 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "import quandl\n",
+ "import numpy as np\n",
+ "import pandas as pd\n",
+ "quandl.ApiConfig.api_key = 'tAyfv1zpWnyhmDsp91yv'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "aapl_table = quandl.get('WIKI/AAPL')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "aapl = aapl_table['Adj. Close']['2017']"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-01-31 120.932434\n",
+ "2017-02-28 136.551200\n",
+ "2017-03-31 143.532630\n",
+ "2017-04-30 144.179981\n",
+ "2017-05-31 156.100000\n",
+ "2017-06-30 155.450000\n",
+ "2017-07-31 153.460000\n",
+ "Freq: M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 6,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "aapl.resample('M').max()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "by_week = aapl.resample('W').mean()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-01-31 1.788740\n",
+ "2017-03-31 4.341378\n",
+ "2017-05-31 5.476627\n",
+ "2017-07-31 3.970133\n",
+ "Freq: 2M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "twomon = aapl.resample('2M').std()\n",
+ "twomon"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-01-31 120.337440\n",
+ "2017-02-28 136.431689\n",
+ "2017-03-31 143.074505\n",
+ "2017-04-30 143.064546\n",
+ "2017-05-31 152.760000\n",
+ "2017-06-30 144.020000\n",
+ "2017-07-31 150.560000\n",
+ "Freq: M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 9,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "last_day = aapl.resample('M').agg(lambda x: x[-1])\n",
+ "last_day"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-01-31 0.045940\n",
+ "2017-02-28 0.070409\n",
+ "2017-03-31 0.033823\n",
+ "2017-04-30 -0.007736\n",
+ "2017-05-31 0.039829\n",
+ "2017-06-30 -0.073528\n",
+ "2017-07-31 0.044902\n",
+ "Freq: M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 10,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "monthly_return = aapl.resample('M').agg(lambda x: x[-1]/x[1] - 1)\n",
+ "monthly_return"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.0219483380858\n",
+ "0.0481467535218\n",
+ "0.0704090212384\n"
+ ]
+ }
+ ],
+ "source": [
+ "print monthly_return.mean()\n",
+ "print monthly_return.std()\n",
+ "print monthly_return.max()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Date\n",
+ "2017-01-31 NaN\n",
+ "2017-02-28 16.094249\n",
+ "2017-03-31 6.642816\n",
+ "2017-04-30 -0.009959\n",
+ "2017-05-31 9.695454\n",
+ "2017-06-30 -8.740000\n",
+ "2017-07-31 6.540000\n",
+ "Freq: M, Name: Adj. Close, dtype: float64\n",
+ "Date\n",
+ "2017-01-31 NaN\n",
+ "2017-02-28 0.133743\n",
+ "2017-03-31 0.048690\n",
+ "2017-04-30 -0.000070\n",
+ "2017-05-31 0.067770\n",
+ "2017-06-30 -0.057214\n",
+ "2017-07-31 0.045410\n",
+ "Freq: M, Name: Adj. Close, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print last_day.diff()\n",
+ "print last_day.pct_change()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "count 143.000000\n",
+ "mean 140.469674\n",
+ "std 10.969137\n",
+ "min 115.051914\n",
+ "25% 136.257402\n",
+ "50% 143.064546\n",
+ "75% 147.339407\n",
+ "max 156.100000\n",
+ "Name: Adj. Close, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print aapl.describe()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-02-28 0.133743\n",
+ "2017-03-31 0.048690\n",
+ "2017-04-30 -0.000070\n",
+ "2017-05-31 0.067770\n",
+ "2017-06-30 -0.057214\n",
+ "2017-07-31 0.045410\n",
+ "Freq: M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 14,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "daily_return = last_day.pct_change()\n",
+ "daily_return.dropna()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Date\n",
+ "2017-01-31 5.880519\n",
+ "2017-02-28 9.093671\n",
+ "2017-03-31 5.417829\n",
+ "2017-04-30 4.073331\n",
+ "2017-05-31 10.167192\n",
+ "2017-06-30 13.180000\n",
+ "2017-07-31 10.730000\n",
+ "Freq: M, Name: Adj. Close, dtype: float64"
+ ]
+ },
+ "execution_count": 15,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "aapl.resample('M').agg(lambda x: max(x) - min(x))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " AAPL GOOG IBM\n",
+ "2017-07-03 143.50 898.70 155.58\n",
+ "2017-07-04 144.09 911.71 153.67\n",
+ "2017-07-05 142.73 906.69 152.36\n",
+ "2017-07-06 144.18 918.59 152.94\n",
+ "2017-07-07 143.77 926.99 153.49\n"
+ ]
+ }
+ ],
+ "source": [
+ "dict = {'AAPL': [143.5, 144.09, 142.73, 144.18, 143.77],'GOOG':[898.7, 911.71, 906.69, 918.59, 926.99],\n",
+ " 'IBM':[155.58, 153.67, 152.36, 152.94, 153.49]}\n",
+ "data_index = pd.date_range('2017-07-03',periods = 5, freq = 'D')\n",
+ "df = pd.DataFrame(dict, index = data_index)\n",
+ "print df"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " AAPL GOOG\n",
+ "0 143.50 898.70\n",
+ "1 144.09 911.71\n",
+ "2 142.73 906.69\n",
+ "3 144.18 918.59\n",
+ "4 143.77 926.99\n"
+ ]
+ }
+ ],
+ "source": [
+ "s1 = pd.Series([143.5, 144.09, 142.73, 144.18, 143.77], name = 'AAPL')\n",
+ "s2 = pd.Series([898.7, 911.71, 906.69, 918.59, 926.99], name = 'GOOG')\n",
+ "data_frame = pd.concat([s1,s2], axis = 1)\n",
+ "print data_frame"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Index([u'AAPL', u'GOOG', u'IBM'], dtype='object')\n",
+ "2017-07-03 143.50\n",
+ "2017-07-04 144.09\n",
+ "2017-07-05 142.73\n",
+ "2017-07-06 144.18\n",
+ "2017-07-07 143.77\n",
+ "Freq: D, Name: AAPL, dtype: float64\n",
+ "2017-07-03 898.70\n",
+ "2017-07-04 911.71\n",
+ "2017-07-05 906.69\n",
+ "2017-07-06 918.59\n",
+ "2017-07-07 926.99\n",
+ "Freq: D, Name: GOOG, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "print df.columns\n",
+ "print df.AAPL\n",
+ "print df['GOOG']"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Date\n",
+ "2017-07-21 150.27\n",
+ "2017-07-24 152.09\n",
+ "2017-07-25 152.74\n",
+ "2017-07-26 153.46\n",
+ "2017-07-27 150.56\n",
+ "Name: Close, dtype: float64\n",
+ "Date\n",
+ "2017-07-21 24671002.0\n",
+ "2017-07-24 21122730.0\n",
+ "2017-07-25 18612649.0\n",
+ "2017-07-26 15172136.0\n",
+ "2017-07-27 32175875.0\n",
+ "Name: Adj. Volume, dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "df = aapl_table\n",
+ "print df.Close.tail(5)\n",
+ "print df['Adj. Volume'].tail(5)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close Volume Ex-Dividend \\\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34 64416504.0 0.0 \n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 35216277.0 0.0 \n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 25888449.0 0.0 \n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 68531478.0 0.0 \n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 42307212.0 0.0 \n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 35836356.0 0.0 \n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 27733688.0 0.0 \n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 29662406.0 0.0 \n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 36379106.0 0.0 \n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 26419398.0 0.0 \n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 36162258.0 0.0 \n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 30586265.0 0.0 \n",
+ "\n",
+ " Split Ratio Adj. Open Adj. High Adj. Low Adj. Close \\\n",
+ "Date \n",
+ "2016-01-31 1.0 91.952819 94.426495 91.525989 94.426495 \n",
+ "2016-02-29 1.0 94.466655 95.802804 94.261844 94.300856 \n",
+ "2016-03-31 1.0 107.008893 107.184446 106.189649 106.296931 \n",
+ "2016-04-30 1.0 91.667571 92.379533 90.224141 91.423748 \n",
+ "2016-05-31 1.0 97.732787 98.517789 96.967410 97.987913 \n",
+ "2016-06-30 1.0 92.669522 93.974588 92.532147 93.807775 \n",
+ "2016-07-31 1.0 102.236738 102.589989 101.736299 102.256363 \n",
+ "2016-08-31 1.0 104.237384 105.135033 104.217653 104.671460 \n",
+ "2016-09-30 1.0 110.945828 111.843576 110.294715 111.527885 \n",
+ "2016-10-31 1.0 112.119806 112.691997 111.675865 112.011287 \n",
+ "2016-11-30 1.0 110.629129 111.263789 109.349893 109.597807 \n",
+ "2016-12-31 1.0 115.676657 116.222068 114.466837 114.853583 \n",
+ "\n",
+ " Adj. Volume \n",
+ "Date \n",
+ "2016-01-31 64416504.0 \n",
+ "2016-02-29 35216277.0 \n",
+ "2016-03-31 25888449.0 \n",
+ "2016-04-30 68531478.0 \n",
+ "2016-05-31 42307212.0 \n",
+ "2016-06-30 35836356.0 \n",
+ "2016-07-31 27733688.0 \n",
+ "2016-08-31 29662406.0 \n",
+ "2016-09-30 36379106.0 \n",
+ "2016-10-31 26419398.0 \n",
+ "2016-11-30 36162258.0 \n",
+ "2016-12-31 30586265.0 \n"
+ ]
+ }
+ ],
+ "source": [
+ "aapl_2016 = df['2016']\n",
+ "aapl_month = aapl_2016.resample('M').agg(lambda x: x[-1])\n",
+ "print aapl_month"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34\n",
+ "2016-02-29 96.86 98.2300 96.65 96.69\n",
+ "2016-03-31 109.72 109.9000 108.88 108.99\n",
+ "2016-04-30 93.99 94.7200 92.51 93.74\n",
+ "2016-05-31 99.60 100.4000 98.82 99.86\n",
+ "2016-06-30 94.44 95.7700 94.30 95.60\n",
+ "2016-07-31 104.19 104.5500 103.68 104.21\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82\n"
+ ]
+ }
+ ],
+ "source": [
+ "aapl_bar = aapl_month[['Open', 'High', 'Low', 'Close']]\n",
+ "print aapl_bar"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close\n",
+ "Date \n",
+ "2016-03-31 109.72 109.90 108.88 108.99\n",
+ "2016-04-30 93.99 94.72 92.51 93.74\n",
+ "2016-05-31 99.60 100.40 98.82 99.86\n",
+ "2016-06-30 94.44 95.77 94.30 95.60\n"
+ ]
+ }
+ ],
+ "source": [
+ "print aapl_month.loc['2016-03':'2016-06',['Open', 'High', 'Low', 'Close']]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close\n",
+ "Date \n",
+ "2016-03-31 109.72 109.9000 108.88 108.99\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82\n"
+ ]
+ }
+ ],
+ "source": [
+ "above = aapl_bar[aapl_bar.Close > np.mean(aapl_bar.Close)]\n",
+ "print above"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34 NaN\n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 -0.006678\n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 0.127211\n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 -0.139921\n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 0.065287\n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 -0.042660\n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 0.090063\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 0.018136\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 0.065504\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 0.004334\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 -0.026599\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 0.047955\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/usr/local/lib/python2.7/site-packages/ipykernel_launcher.py:1: SettingWithCopyWarning: \n",
+ "A value is trying to be set on a copy of a slice from a DataFrame.\n",
+ "Try using .loc[row_indexer,col_indexer] = value instead\n",
+ "\n",
+ "See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
+ " \"\"\"Entry point for launching an IPython kernel.\n"
+ ]
+ }
+ ],
+ "source": [
+ "aapl_bar['rate_return'] = aapl_bar.Close.pct_change()\n",
+ "print aapl_bar"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return\n",
+ "Date \n",
+ "2016-01-31 False False False False True\n",
+ "2016-02-29 False False False False False\n",
+ "2016-03-31 False False False False False\n",
+ "2016-04-30 False False False False False\n",
+ "2016-05-31 False False False False False\n",
+ "2016-06-30 False False False False False\n",
+ "2016-07-31 False False False False False\n",
+ "2016-08-31 False False False False False\n",
+ "2016-09-30 False False False False False\n",
+ "2016-10-31 False False False False False\n",
+ "2016-11-30 False False False False False\n",
+ "2016-12-31 False False False False False\n",
+ "\n",
+ "------------------ separate line -----------------\n",
+ "\n",
+ " Open High Low Close rate_return\n",
+ "count 12 12 12 12 12\n",
+ "unique 1 1 1 1 2\n",
+ "top False False False False False\n",
+ "freq 12 12 12 12 11\n"
+ ]
+ }
+ ],
+ "source": [
+ "missing = aapl_bar.isnull()\n",
+ "print missing\n",
+ "print '\\n------------------ separate line -----------------\\n'\n",
+ "print missing.describe()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return\n",
+ "Date \n",
+ "2016-01-31 False False False False True\n"
+ ]
+ }
+ ],
+ "source": [
+ "print missing[missing.rate_return == True]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return\n",
+ "Date \n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 -0.006678\n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 0.127211\n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 -0.139921\n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 0.065287\n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 -0.042660\n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 0.090063\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 0.018136\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 0.065504\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 0.004334\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 -0.026599\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 0.047955\n",
+ "\n",
+ "---------------------- separate line--------------------\n",
+ "\n",
+ " Open High Low Close rate_return\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34 0.000000\n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 -0.006678\n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 0.127211\n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 -0.139921\n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 0.065287\n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 -0.042660\n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 0.090063\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 0.018136\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 0.065504\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 0.004334\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 -0.026599\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 0.047955\n"
+ ]
+ }
+ ],
+ "source": [
+ "drop = aapl_bar.dropna()\n",
+ "print drop\n",
+ "print '\\n---------------------- separate line--------------------\\n'\n",
+ "fill = aapl_bar.fillna(0)\n",
+ "print fill"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " AAPL GOOG\n",
+ "0 143.50 898.70\n",
+ "1 144.09 911.71\n",
+ "2 142.73 906.69\n",
+ "3 144.18 918.59\n",
+ "4 143.77 926.99\n"
+ ]
+ }
+ ],
+ "source": [
+ "s1 = pd.Series([143.5, 144.09, 142.73, 144.18, 143.77], name = 'AAPL')\n",
+ "s2 = pd.Series([898.7, 911.71, 906.69, 918.59, 926.99], name = 'GOOG')\n",
+ "data_frame = pd.concat([s1,s2], axis = 1)\n",
+ "print data_frame"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 29,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Date\n",
+ "2016-01-31 4.578210\n",
+ "2016-02-29 4.571510\n",
+ "2016-03-31 4.691256\n",
+ "2016-04-30 4.540525\n",
+ "2016-05-31 4.603769\n",
+ "2016-06-30 4.560173\n",
+ "2016-07-31 4.646408\n",
+ "2016-08-31 4.664382\n",
+ "2016-09-30 4.727830\n",
+ "2016-10-31 4.732155\n",
+ "2016-11-30 4.705197\n",
+ "2016-12-31 4.752037\n",
+ "Freq: M, Name: log_price, dtype: float64\n",
+ "\n",
+ "---------------------- separate line--------------------\n",
+ "\n",
+ " Open High Low Close rate_return log_price\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34 NaN 4.578210\n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 -0.006678 4.571510\n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 0.127211 4.691256\n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 -0.139921 4.540525\n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 0.065287 4.603769\n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 -0.042660 4.560173\n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 0.090063 4.646408\n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 0.018136 4.664382\n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 0.065504 4.727830\n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 0.004334 4.732155\n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 -0.026599 4.705197\n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 0.047955 4.752037\n"
+ ]
+ }
+ ],
+ "source": [
+ "log_price = np.log(aapl_bar.Close)\n",
+ "log_price.name = 'log_price'\n",
+ "print log_price\n",
+ "print '\\n---------------------- separate line--------------------\\n'\n",
+ "concat = pd.concat([aapl_bar, log_price], axis = 1)\n",
+ "print concat"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 30,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Volume Split Ratio\n",
+ "Date \n",
+ "2016-10-31 26419398.0 1.0\n",
+ "2016-11-30 36162258.0 1.0\n",
+ "2016-12-31 30586265.0 1.0\n",
+ "2017-01-31 49200993.0 1.0\n",
+ "2017-02-28 23482860.0 1.0\n",
+ "2017-03-31 19661651.0 1.0\n",
+ "2017-04-30 20247187.0 1.0\n",
+ "\n",
+ "---------------------- separate line--------------------\n",
+ "\n",
+ " Open High Low Close\n",
+ "Date \n",
+ "2016-10-31 113.65 114.230 113.20 113.54\n",
+ "2016-11-30 111.56 112.200 110.27 110.52\n",
+ "2016-12-31 116.65 117.200 115.43 115.82\n",
+ "2017-01-31 121.15 121.390 120.62 121.35\n",
+ "2017-02-28 137.08 137.435 136.70 136.99\n",
+ "2017-03-31 143.72 144.270 143.01 143.66\n",
+ "2017-04-30 144.09 144.300 143.27 143.65\n"
+ ]
+ }
+ ],
+ "source": [
+ "df_volume = aapl_table.loc['2016-10':'2017-04',['Volume', 'Split Ratio']].resample('M').agg(lambda x: x[-1])\n",
+ "print df_volume\n",
+ "print '\\n---------------------- separate line--------------------\\n'\n",
+ "df_2017 = aapl_table.loc['2016-10':'2017-04',['Open', 'High', 'Low', 'Close']].resample('M').agg(lambda x: x[-1])\n",
+ "print df_2017"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return Volume \\\n",
+ "Date \n",
+ "2016-01-31 94.79 97.3400 94.35 97.34 NaN NaN \n",
+ "2016-02-29 96.86 98.2300 96.65 96.69 -0.006678 NaN \n",
+ "2016-03-31 109.72 109.9000 108.88 108.99 0.127211 NaN \n",
+ "2016-04-30 93.99 94.7200 92.51 93.74 -0.139921 NaN \n",
+ "2016-05-31 99.60 100.4000 98.82 99.86 0.065287 NaN \n",
+ "2016-06-30 94.44 95.7700 94.30 95.60 -0.042660 NaN \n",
+ "2016-07-31 104.19 104.5500 103.68 104.21 0.090063 NaN \n",
+ "2016-08-31 105.66 106.5699 105.64 106.10 0.018136 NaN \n",
+ "2016-09-30 112.46 113.3700 111.80 113.05 0.065504 NaN \n",
+ "2016-10-31 113.65 114.2300 113.20 113.54 0.004334 26419398.0 \n",
+ "2016-11-30 111.56 112.2000 110.27 110.52 -0.026599 36162258.0 \n",
+ "2016-12-31 116.65 117.2000 115.43 115.82 0.047955 30586265.0 \n",
+ "2017-01-31 NaN NaN NaN NaN NaN 49200993.0 \n",
+ "2017-02-28 NaN NaN NaN NaN NaN 23482860.0 \n",
+ "2017-03-31 NaN NaN NaN NaN NaN 19661651.0 \n",
+ "2017-04-30 NaN NaN NaN NaN NaN 20247187.0 \n",
+ "\n",
+ " Split Ratio \n",
+ "Date \n",
+ "2016-01-31 NaN \n",
+ "2016-02-29 NaN \n",
+ "2016-03-31 NaN \n",
+ "2016-04-30 NaN \n",
+ "2016-05-31 NaN \n",
+ "2016-06-30 NaN \n",
+ "2016-07-31 NaN \n",
+ "2016-08-31 NaN \n",
+ "2016-09-30 NaN \n",
+ "2016-10-31 1.0 \n",
+ "2016-11-30 1.0 \n",
+ "2016-12-31 1.0 \n",
+ "2017-01-31 1.0 \n",
+ "2017-02-28 1.0 \n",
+ "2017-03-31 1.0 \n",
+ "2017-04-30 1.0 \n"
+ ]
+ }
+ ],
+ "source": [
+ "concat = pd.concat([aapl_bar,df_volume],axis = 1)\n",
+ "print concat"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 32,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Open High Low Close rate_return Volume \\\n",
+ "Date \n",
+ "2016-10-31 113.65 114.23 113.20 113.54 0.004334 26419398.0 \n",
+ "2016-11-30 111.56 112.20 110.27 110.52 -0.026599 36162258.0 \n",
+ "2016-12-31 116.65 117.20 115.43 115.82 0.047955 30586265.0 \n",
+ "\n",
+ " Split Ratio \n",
+ "Date \n",
+ "2016-10-31 1.0 \n",
+ "2016-11-30 1.0 \n",
+ "2016-12-31 1.0 \n"
+ ]
+ }
+ ],
+ "source": [
+ "concat = pd.concat([aapl_bar,df_volume],axis = 1, join = 'inner')\n",
+ "print concat"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 33,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Close High Low Open rate_return\n",
+ "Date \n",
+ "2016-01-31 97.34 97.3400 94.35 94.79 NaN\n",
+ "2016-02-29 96.69 98.2300 96.65 96.86 -0.006678\n",
+ "2016-03-31 108.99 109.9000 108.88 109.72 0.127211\n",
+ "2016-04-30 93.74 94.7200 92.51 93.99 -0.139921\n",
+ "2016-05-31 99.86 100.4000 98.82 99.60 0.065287\n",
+ "2016-06-30 95.60 95.7700 94.30 94.44 -0.042660\n",
+ "2016-07-31 104.21 104.5500 103.68 104.19 0.090063\n",
+ "2016-08-31 106.10 106.5699 105.64 105.66 0.018136\n",
+ "2016-09-30 113.05 113.3700 111.80 112.46 0.065504\n",
+ "2016-10-31 113.54 114.2300 113.20 113.65 0.004334\n",
+ "2016-11-30 110.52 112.2000 110.27 111.56 -0.026599\n",
+ "2016-12-31 115.82 117.2000 115.43 116.65 0.047955\n",
+ "2016-10-31 113.54 114.2300 113.20 113.65 NaN\n",
+ "2016-11-30 110.52 112.2000 110.27 111.56 NaN\n",
+ "2016-12-31 115.82 117.2000 115.43 116.65 NaN\n",
+ "2017-01-31 121.35 121.3900 120.62 121.15 NaN\n",
+ "2017-02-28 136.99 137.4350 136.70 137.08 NaN\n",
+ "2017-03-31 143.66 144.2700 143.01 143.72 NaN\n",
+ "2017-04-30 143.65 144.3000 143.27 144.09 NaN\n"
+ ]
+ }
+ ],
+ "source": [
+ "append = aapl_bar.append(df_2017)\n",
+ "print append"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 34,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Close High Low Open rate_return\n",
+ "Date \n",
+ "2016-01-31 97.34 97.3400 94.35 94.79 NaN\n",
+ "2016-02-29 96.69 98.2300 96.65 96.86 -0.006678\n",
+ "2016-03-31 108.99 109.9000 108.88 109.72 0.127211\n",
+ "2016-04-30 93.74 94.7200 92.51 93.99 -0.139921\n",
+ "2016-05-31 99.86 100.4000 98.82 99.60 0.065287\n",
+ "2016-06-30 95.60 95.7700 94.30 94.44 -0.042660\n",
+ "2016-07-31 104.21 104.5500 103.68 104.19 0.090063\n",
+ "2016-08-31 106.10 106.5699 105.64 105.66 0.018136\n",
+ "2016-09-30 113.05 113.3700 111.80 112.46 0.065504\n",
+ "2016-10-31 113.54 114.2300 113.20 113.65 0.004334\n",
+ "2016-11-30 110.52 112.2000 110.27 111.56 -0.026599\n",
+ "2016-12-31 115.82 117.2000 115.43 116.65 0.047955\n",
+ "2016-10-31 113.54 114.2300 113.20 113.65 NaN\n",
+ "2016-11-30 110.52 112.2000 110.27 111.56 NaN\n",
+ "2016-12-31 115.82 117.2000 115.43 116.65 NaN\n",
+ "2017-01-31 121.35 121.3900 120.62 121.15 NaN\n",
+ "2017-02-28 136.99 137.4350 136.70 137.08 NaN\n",
+ "2017-03-31 143.66 144.2700 143.01 143.72 NaN\n",
+ "2017-04-30 143.65 144.3000 143.27 144.09 NaN\n"
+ ]
+ }
+ ],
+ "source": [
+ "concat = pd.concat([aapl_bar, df_2017], axis = 0)\n",
+ "print concat"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Change Close High Low Open rate_return\n",
+ "Date \n",
+ "2016-01-31 NaN 97.34 97.3400 94.35 94.79 NaN\n",
+ "2016-02-29 NaN 96.69 98.2300 96.65 96.86 -0.006678\n",
+ "2016-03-31 NaN 108.99 109.9000 108.88 109.72 0.127211\n",
+ "2016-04-30 NaN 93.74 94.7200 92.51 93.99 -0.139921\n",
+ "2016-05-31 NaN 99.86 100.4000 98.82 99.60 0.065287\n",
+ "2016-06-30 NaN 95.60 95.7700 94.30 94.44 -0.042660\n",
+ "2016-07-31 NaN 104.21 104.5500 103.68 104.19 0.090063\n",
+ "2016-08-31 NaN 106.10 106.5699 105.64 105.66 0.018136\n",
+ "2016-09-30 NaN 113.05 113.3700 111.80 112.46 0.065504\n",
+ "2016-10-31 NaN 113.54 114.2300 113.20 113.65 0.004334\n",
+ "2016-11-30 NaN 110.52 112.2000 110.27 111.56 -0.026599\n",
+ "2016-12-31 NaN 115.82 117.2000 115.43 116.65 0.047955\n",
+ "2016-10-31 113.65 113.54 114.2300 113.20 NaN NaN\n",
+ "2016-11-30 111.56 110.52 112.2000 110.27 NaN NaN\n",
+ "2016-12-31 116.65 115.82 117.2000 115.43 NaN NaN\n",
+ "2017-01-31 121.15 121.35 121.3900 120.62 NaN NaN\n",
+ "2017-02-28 137.08 136.99 137.4350 136.70 NaN NaN\n",
+ "2017-03-31 143.72 143.66 144.2700 143.01 NaN NaN\n",
+ "2017-04-30 144.09 143.65 144.3000 143.27 NaN NaN\n"
+ ]
+ }
+ ],
+ "source": [
+ "df_2017.columns = ['Change', 'High','Low','Close']\n",
+ "concat = pd.concat([aapl_bar, df_2017], axis = 0)\n",
+ "print concat"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 36,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Change Close High Low Open rate_return\n",
+ "Date \n",
+ "2016-01-31 NaN 97.34 97.3400 94.35 94.79 NaN\n",
+ "2016-02-29 NaN 96.69 98.2300 96.65 96.86 -0.006678\n",
+ "2016-03-31 NaN 108.99 109.9000 108.88 109.72 0.127211\n",
+ "2016-04-30 NaN 93.74 94.7200 92.51 93.99 -0.139921\n",
+ "2016-05-31 NaN 99.86 100.4000 98.82 99.60 0.065287\n",
+ "2016-06-30 NaN 95.60 95.7700 94.30 94.44 -0.042660\n",
+ "2016-07-31 NaN 104.21 104.5500 103.68 104.19 0.090063\n",
+ "2016-08-31 NaN 106.10 106.5699 105.64 105.66 0.018136\n",
+ "2016-09-30 NaN 113.05 113.3700 111.80 112.46 0.065504\n",
+ "2016-10-31 NaN 113.54 114.2300 113.20 113.65 0.004334\n",
+ "2016-11-30 NaN 110.52 112.2000 110.27 111.56 -0.026599\n",
+ "2016-12-31 NaN 115.82 117.2000 115.43 116.65 0.047955\n",
+ "2016-10-31 113.65 113.54 114.2300 113.20 NaN NaN\n",
+ "2016-11-30 111.56 110.52 112.2000 110.27 NaN NaN\n",
+ "2016-12-31 116.65 115.82 117.2000 115.43 NaN NaN\n",
+ "2017-01-31 121.15 121.35 121.3900 120.62 NaN NaN\n",
+ "2017-02-28 137.08 136.99 137.4350 136.70 NaN NaN\n",
+ "2017-03-31 143.72 143.66 144.2700 143.01 NaN NaN\n",
+ "2017-04-30 144.09 143.65 144.3000 143.27 NaN NaN\n"
+ ]
+ }
+ ],
+ "source": [
+ "concat = pd.concat([aapl_bar, df_2017], axis = 0)\n",
+ "print concat"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial6 Rate of Return, Mean and Variance.html b/Introduction to Financial Python/Tutorial6 Rate of Return, Mean and Variance.html
new file mode 100644
index 0000000..ef90704
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial6 Rate of Return, Mean and Variance.html
@@ -0,0 +1,86 @@
+Introduction
+In this chapter we are going to introduce some basic concepts in quantitative finance. We start with rate of return, mean and variance. You may think it's simple to calculate these values, however, there are number of different methods to calculate them. It's important to choose the appropriate calculation methods case by case.
+Rate of Return
+Single-period Return
+The single-period rate of return can be calculated as following:
+\[r = \frac{p_t}{p_0} - 1 = \frac{p_t - p_0}{p_0}\]
+Where \(r\) is the rate of return, \(p_t\) is the asset price at time \(t\), and \(p_0\) is the asset price at time 0.
+import numpy as np
+rate_return = 102.0/100 - 1
+print rate_return
+
+Let's say we bought a stock at $100, and half a year later it will grow to $102. A year later the price will come to $104. How to calculate our total return?
+Well, we can either deem it as a single-period:
+\[r = 104/100 - 1 = 0.04\]
+or as a two-stage period:
+\[ r = (1+r_1)*(1+r_2) - 1 = \frac{102}{100} * \frac{104}{102} -1 = 0.04\]
+Here we make calculations twice a year. It's called semi-annual compounding. How about quarterly compounding?
+Let's assume the stock prices at the end of each quarter are \(p_1, p_2, p_3, p_4\) respectively.
+\[r = (1+r_1)*(1+r_2)*(1+r_3)*(1+r_4) -1\]
+The rate of return we calculate here is called cumulative return or overall return. It measures the total return of this asset over a period of time.
+Now consider the following situation: we have two strategies: strategy A and strategy B. We backtested strategy A for 1 years and the cumulative return is 20%, while we backtested strategy B and the cumulative return is 65%. Which strategy has a high rate of return? Our commonly used method is to convert all the returns into compounding annual return, regardless of the investing horizon of each strategy. We can compare the returns of strategies with different time horizon now!
+\[(1+r)^3 = 1+0.65\]
+\[ r = \sqrt[3]{1.65} - 1\ = 0.18167\]
+Strategy A has an higher compounding annual return!
+Logarithm Return
+We introduced compounding annual return above, which is a kind of effective rate of return. You can regard it as a 'hypothetical return'. Strategy B might never have a 18.167% rate of rate annually during the 3-year backtesting period. However, if we assume that the strategy has a 18.167% rate of return every year, it has the same cumulative return over the 3 years.
+As we mentioned previously, if we assume a strategy is quarterly compounding, the relation between quarterly effective rate of return and annual return is:
+\[(1+\frac{r}{4})^4 = 1+r\]
+More generally, if the times of compounding in one year is \(n\) and the annual rate of return is \(r\), the relation is given by:
+\[(1+\frac{r}{n})^n = 1+r\]
+Now imagine the stock markets. The prices of your assets is changing every second, or even every millisecond. If the times of compounding, or n, approach to infinite, this is called continuous compounding. The calculation formula is given below:
+\[\lim_{n \to \infty }(1+\frac{r}{n})^n = e^r\]
+From the above limitation equation, we know that if we assume continuous compounding:
+\[e^r = 1 + r = \frac{p_t}{p_0}\]
+Then we take \(ln\) on both side of the equation:
+\[r = ln\frac{p_t}{p_0} = lnp_t - lnp_0\]
+Here we got the logarithmic return, or continuously compounded return.
+This is frequently used when calculating returns, because once we take logarithm of asset prices, we can calculate the logarithm return by simply doing a subtraction. Here we use Apple stock prices as a example:
+import quandl
+import numpy as np
+quandl.ApiConfig.api_key = 'zNXvSaz2oX5afVGKjf6o'
+aapl_table = quandl.get('WIKI/AAPL')
+aapl = aapl_table.loc['2017-3',['Open','Close']]
+aapl['log_price'] = np.log(aapl.Close)
+aapl['log_return'] = np.log_price.diff()
+print aapl
+
+Here we calculated the daily logarithmic return of Apple stock. Given that we know the daily logarithm return of in this month, we can calculate the monthly return by simply sum all the daily returns up.
+month_return = aapl.log_return.sum()
+print month_return
+
+It may sounds incorrect to sum up the daily returns, but we can prove that it's mathematically correct. Let's assume the stock prices in a period of time are represented by \([p_0, p_1, p_2, p_3.....p_n]\). Then the cumulative rate of return is given by:
+\[1+r = ln\frac{p_t}{p_0} = ln\frac{p_t}{p_{t-1}} + ln\frac{p_{t-1}}{p_{t-2}}+......+ln\frac{p_1}{p_0}\]
+According to the equation above, we can simple sum up each logarithmic return in a period to get the cumulative return. The convenience of this method is also one of the reasons why we use logarithmic return in quantitative finance.
+Mean
+Arithmetic Mean
+Mean is a measure of the central tendency of a data series. It capture the key character of the distribution of the data series. When we talk about mean, by default it refers to arithmetic mean. It's defined as the sum of the values divided by the number of observations:
+\[\mu = \frac{\sum_{i = 1}^{n}x_i}{n}\]
+Where \((x_1,x_2,x_3.....x_n)\) is our data series.
+In python we can use NumPy.mean() to do the calculation:
+print np.mean(aapl.log_price)
+
+Geometric Mean
+The geometric mean is an average that is useful for data series of positive numbers that are better interpreted according to their product, such as growth rate. It's calculated by:
+\[\bar{x} = \sqrt[n]{x_1x_2x_3...x_n}\]
+Let's calculate the geometric mean of a series of single-period return:
+\[1+\bar{r} = \sqrt[n]{\frac{p_t}{p_{t-1}}*\frac{p_{t-1}}{p_{t-2}}*...*\frac{p_2}{p_1}}\]
+\[(1+\bar{r}) = \sqrt[n]{\frac{p_t}{p_0}}\]
+Now the equation becomes the form which we are familiar with:
+\[(1+\bar{r})^n = \frac{p_t}{p_0}\]
+This is why we said it make sense when applied to growth rates.
+Variance and Standard Deviation
+Variance
+Variance is a measure of dispersion. In finance, most of the time variance is a synonym for risk. The higher the variance of an asset price is, the higher risk the asset bears. Variance is usually represented by \(\sigma\), and it's calculated by
+\[\sigma^2 = \frac{\sum_{i = 1}^{n}(x_i- \mu)^2}{n}\]
+In python we can use NumPy.var to calculate it:
+print np.var(aapl.log_price)
+
+Standard Deviation
+The most commonly used measure of dispersion in finance is standard deviation. It's usually represented by \(\sigma\). It's obvious to see the relation between standard deviation and variance:
+\[\sigma = \sqrt{\sigma^2} = \sqrt{\frac{\sum_{i = 1}^{n}(x_i- \mu)^2}{n}}\]
+NumPy also provides us a method to calculate standard deviation.
+print np.std(aapl.log_price)
+
+Summary
+We introduced different types of rate of return in this chapter, which could be a little bit tricky when we calculate them. Mean and standard deviation are also very important concepts when we conduct hypothesis test or measure the risk associated with a asset. We will use those comcepts intensively in our later chapter.
diff --git a/Introduction to Financial Python/Tutorial7 Random Variable and Distributions.ipynb b/Introduction to Financial Python/Tutorial7 Random Variable and Distributions.ipynb
new file mode 100644
index 0000000..738f8e7
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial7 Random Variable and Distributions.ipynb
@@ -0,0 +1,376 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[3 4 2 ..., 6 3 6]\n"
+ ]
+ }
+ ],
+ "source": [
+ "import random\n",
+ "import matplotlib.pyplot as plt\n",
+ "import numpy as np\n",
+ "import pandas as pd\n",
+ "def dice():\n",
+ " number= [1,2,3,4,5,6]\n",
+ " return random.choice(number)\n",
+ " \n",
+ "series = np.array([dice() for x in range(10000)])\n",
+ "print series\n",
+ "from math import factorial"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABJwAAAJQCAYAAADL1H4pAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3X/Q5XV93/3X28UfZDeiCXZLgAbSIbYo903kGvSeNPba\nmB+r8a6mzbQwViWmrqnYiQ3TBtvp6N3UjtOEpqNJbYhwoxPixmosDEIMIaE2mdLIGuqCSlzNZmRr\n2SaYJRpuKvi+/9jvNldwgUP5nB/XtY/HzDV7zvc651zvy/18xuG553y/1d0BAAAAgFGesuwBAAAA\nANhaBCcAAAAAhhKcAAAAABhKcAIAAABgKMEJAAAAgKEEJwAAAACGEpwAAAAAGEpwAgAAAGAowQkA\nAACAoU5a9gDzcuqpp/ZZZ5217DGetK985SvZvn37sseAlWevwGzsFZiNvQKzsVdgNltpr+zbt+8P\nu/s5j/e4LRuczjrrrNx+++3LHuNJu/XWW7O+vr7sMWDl2SswG3sFZmOvwGzsFZjNVtorVfUHszzO\nR+oAAAAAGEpwAgAAAGAowQkAAACAoQQnAAAAAIYSnAAAAAAYSnACAAAAYCjBCQAAAIChBCcAAAAA\nhhKcAAAAABhKcAIAAABgqLkFp6q6uqoOV9WdG479clXdMX0drKo7puNnVdUDG7737zY854Kq2l9V\nB6rqnVVV85oZAAAAgCfvpDm+9jVJfjbJ+44d6O6/c+x2VV2R5MiGx3+uu88/zuu8O8nrk/yXJDcm\n2Z3kpjnMCwAAAMAAc3uHU3d/LMl9x/ve9C6lv53k/Y/1GlV1WpJndvdt3d05Gq9eOXpWAAAAAMZZ\n1jmcvivJvd392Q3Hzq6q362q/1hV3zUdOz3JPRsec890DAAAAIAVNc+P1D2Wi/Pn3930xSR/qbv/\nqKouSPIfqup5T/RFq2pPkj1JsnPnztx6660jZl2qL3/5y1vi94B5s1dgNvYKzMZegdnYKzCbE3Gv\nLDw4VdVJSf5mkguOHevuB5M8ON3eV1WfS/LtSQ4lOWPD08+Yjh1Xd1+Z5MokWVtb6/X19dHjL9yt\nt96arfB7wLzZKzAbewVmY6/AbOwVmM2JuFeW8ZG670nyme7+Xx+Vq6rnVNW26fa3JTknyee7+4tJ\n7q+qF03nfXpNkuuWMDMAAAAAM5pbcKqq9yf5z0meW1X3VNWPTN+6KF9/svAXJ/lkVd2R5INJfrS7\nj51w/I1J3pPkQJLPxRXqAAAAAFba3D5S190XP8rxS45z7ENJPvQoj789yfOHDgcAAADA3CzrKnUA\nAAAAbFGCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUHO7Sh0AAFvbWZd/ZNkjzM1l5z2US1bs\n9zv4jh9Y9ggAMDPvcAIAAABgKMEJAAAAgKEEJwAAAACGEpwAAAAAGEpwAgAAAGAowQkAAACAoQQn\nAAAAAIYSnAAAAAAYSnACAAAAYCjBCQAAAIChTlr2AAAAAKvmrMs/suwRNoXLznsolwz43+rgO35g\nwDTAKvEOJwAAAACGEpwAAAAAGEpwAgAAAGAo53ACgDlZxfN/jDrXxipy/g8AgNUhOAFLNeo/yLfy\nf0SP5D/IAQCARfCROgAAAACGEpwAAAAAGEpwAgAAAGAowQkAAACAoZw0HAAAAE4wq3g13a3smt3b\nlz3CwnmHEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEO5St2K23/oSC5x9YCFOviO\nH1j2CAAAALCpeYcTAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEA\nAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgB\nAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4\nAQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwl\nOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADDW34FRVV1fV4aq6c8Oxt1XVoaq6Y/p62YbvvaWq\nDlTV3VX1/RuO756OHaiqy+c1LwAAAABjzPMdTtck2X2c4z/T3edPXzcmSVWdm+SiJM+bnvNvq2pb\nVW1L8nNJXprk3CQXT48FAAAAYEWdNK8X7u6PVdVZMz78FUn2dveDSX6/qg4kuXD63oHu/nySVNXe\n6bGfGjwuAAAAAINUd8/vxY8Gpxu6+/nT/bcluSTJ/UluT3JZd3+pqn42yW3d/YvT465KctP0Mru7\n++9Nx1+d5IXd/aZH+Xl7kuxJkp07d16wd+/e+fxiC3T4viO594FlT3FiOe/0U5Y9wgll/6EjQ15n\n58mxV2ZgfS/WqPU90lbeK9b34q3iGh9lFfeKNb5YW3l9jzRqr1jfi2eNL9bZp2zLjh07lj3GELt2\n7drX3WuP97i5vcPpUbw7yU8m6enPK5K8btSLd/eVSa5MkrW1tV5fXx/10kvzrmuvyxX7F/3XdGI7\n+Kr1ZY9wQrnk8o8MeZ3LznvIXpmB9b1Yo9b3SFt5r1jfi7eKa3yUVdwr1vhibeX1PdKovWJ9L541\nvljX7N6erdAonoiF/r9od9977HZV/UKSG6a7h5KcueGhZ0zH8hjHAQAAAFhB8zxp+NepqtM23P3B\nJMeuYHd9kouq6ulVdXaSc5L8TpKPJzmnqs6uqqfl6InFr1/kzAAAAAA8MXN7h1NVvT/JepJTq+qe\nJG9Nsl5V5+foR+oOJnlDknT3XVX1gRw9GfhDSS7t7oen13lTko8m2Zbk6u6+a14zAwAAAPDkzfMq\ndRcf5/BVj/H4tyd5+3GO35jkxoGjAQAAADBHC/1IHQAAAABbn+AEAAAAwFCCEwAAAABDCU4AAAAA\nDCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAA\nAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAA\nAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4A\nAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlO\nAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJ\nTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABD\nCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAA\nQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUHMLTlV1\ndVUdrqo7Nxz7qar6TFV9sqo+XFXPmo6fVVUPVNUd09e/2/CcC6pqf1UdqKp3VlXNa2YAAAAAnrx5\nvsPpmiS7H3Hs5iTP7+7/I8nvJXnLhu99rrvPn75+dMPxdyd5fZJzpq9HviYAAAAAK2Ruwam7P5bk\nvkcc+7Xufmi6e1uSMx7rNarqtCTP7O7buruTvC/JK+cxLwAAAABjLPMcTq9LctOG+2dX1e9W1X+s\nqu+ajp2e5J4Nj7lnOgYAAADAiqqjbxya04tXnZXkhu5+/iOO/9Mka0n+Znd3VT09yY7u/qOquiDJ\nf0jyvCTfnuQd3f090/O+K8lPdPfLH+Xn7UmyJ0l27tx5wd69e+fziy3Q4fuO5N4Hlj3FieW8009Z\n9ggnlP2Hjgx5nZ0nx16ZgfW9WKPW90hbea9Y34u3imt8lFXcK9b4Ym3l9T3SqL1ifS+eNb5YZ5+y\nLTt27Fj2GEPs2rVrX3evPd7jTlrEMBtV1SVJXp7kJdPH5NLdDyZ5cLq9r6o+l6Ox6VD+/MfuzpiO\nHVd3X5nkyiRZW1vr9fX1OfwGi/Wua6/LFfsX/td0Qjv4qvVlj3BCueTyjwx5ncvOe8hemYH1vVij\n1vdIW3mvWN+Lt4prfJRV3CvW+GJt5fU90qi9Yn0vnjW+WNfs3p6t0CieiIV+pK6qdif5x0n+Rnf/\n6Ybjz6mqbdPtb8vRk4N/vru/mOT+qnrRdHW61yS5bpEzAwAAAPDEzO2fbarq/UnWk5xaVfckeWuO\nXpXu6UluPtqPctt0RboXJ/nnVfXVJF9L8qPdfeyE42/M0SvenZyj53zaeN4nAAAAAFbM3IJTd198\nnMNXPcpjP5TkQ4/yvduTPP943wMAAABg9SzzKnUAAAAAbEGCEwAAAABDCU4AAAAADCU4AQAAADCU\n4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAw\nlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAA\nMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAA\nADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEA\nAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgB\nAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4\nAQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwl\nOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAM\nNdfgVFVXV9Xhqrpzw7Fvqqqbq+qz05/Pno5XVb2zqg5U1Ser6gUbnvPa6fGfrarXznNmAAAAAJ6c\neb/D6Zokux9x7PIkt3T3OUlume4nyUuTnDN97Uny7uRooEry1iQvTHJhkrcei1QAAAAArJ65Bqfu\n/liS+x5x+BVJ3jvdfm+SV244/r4+6rYkz6qq05J8f5Kbu/u+7v5Skpvz9RELAAAAgBVR3T3fH1B1\nVpIbuvv50/0/7u5nTbcryZe6+1lVdUOSd3T3b03fuyXJTyRZT/KM7v4X0/F/luSB7v7p4/ysPTn6\n7qjs3Lnzgr179871d1uEw/cdyb0PLHuKE8t5p5+y7BFOKPsPHRnyOjtPjr0yA+t7sUat75G28l6x\nvhdvFdf4KKu4V6zxxdrK63ukUXvF+l48a3yxzj5lW3bs2LHsMYbYtWvXvu5ee7zHnbSIYR5Nd3dV\nDSte3X1lkiuTZG1trdfX10e99NK869rrcsX+pf41nXAOvmp92SOcUC65/CNDXuey8x6yV2ZgfS/W\nqPU90lbeK9b34q3iGh9lFfeKNb5YW3l9jzRqr1jfi2eNL9Y1u7dnKzSKJ2IZV6m7d/qoXKY/D0/H\nDyU5c8PjzpiOPdpxAAAAAFbQEw5OVfWUqnrmk/iZ1yc5dqW51ya5bsPx10xXq3tRkiPd/cUkH03y\nfVX17Olk4d83HQMAAABgBc0UnKrql6rqmVW1PcmdST5VVf9ohue9P8l/TvLcqrqnqn4kyTuSfG9V\nfTbJ90z3k+TGJJ9PciDJLyR5Y5J0931JfjLJx6evfz4dAwAAAGAFzfph23O7+/6qelWSm5JcnmRf\nkp96rCd198WP8q2XHOexneTSR3mdq5NcPeOsAAAAACzRrB+pe2pVPTXJK5Nc391fTTLfy9sBAAAA\nsCnNGpx+PsnBJNuTfKyqvjXJ/fMaCgAAAIDNa6aP1HX3O5O8c8OhP6iqXfMZCQAAAIDNbNaThu+s\nqquq6qbp/rn5syvNAQAAAMD/MutH6q5J8tEk3zLd/70kb57HQAAAAABsbrMGp1O7+wNJvpYk3f1Q\nkofnNhUAAAAAm9aswekrVfXNma5MV1UvSnJkblMBAAAAsGnNdNLwJD+e5Pokf7mqfjvJc5L80Nym\nAgAAAGDTmvUqdZ+oqr+e5LlJKsnd3f3VuU4GAAAAwKY061XqLk2yo7vv6u47k+yoqjfOdzQAAAAA\nNqNZz+H0+u7+42N3uvtLSV4/n5EAAAAA2MxmDU7bqqqO3amqbUmeNp+RAAAAANjMZj1p+K8m+eWq\n+vnp/humYwAAAADw58wanH4iRyPT35/u35zkPXOZCAAAAIBNbdar1H0tybunLwAAAAB4VDMFp6r6\nziRvS/Kt03MqSXf3t81vNAAAAAA2o1k/UndVkn+YZF+Sh+c3DgAAAACb3azB6Uh33zTXSQAAAADY\nEmYNTr9ZVT+V5FeSPHjsYHd/Yi5TAQAAALBpzRqcXjj9ubbhWCf57rHjAAAAALDZzXqVul3zHgQA\nAACAreEpszyoqnZW1VVVddN0/9yq+pH5jgYAAADAZjRTcEpyTZKPJvmW6f7vJXnzPAYCAAAAYHOb\nNTid2t0fSPK1JOnuh5I8PLepAAAAANi0Zg1OX6mqb87RE4Wnql6U5MjcpgIAAABg05r1KnU/nuT6\nJH+5qn47yXOS/NDcpgIAAABg03rc4FRVT0nyjCR/Pclzk1SSu7v7q3OeDQAAAIBN6HGDU3d/rap+\nrru/I8ldC5gJAAAAgE1s1nM43VJVf6uqaq7TAAAAALDpzRqc3pDk3yd5sKrur6o/qar75zgXAAAA\nAJvUTCcN7+5vnPcgAAAAAGwNMwWnqnrx8Y5398fGjgMAAADAZjdTcEryjzbcfkaSC5PsS/LdwycC\nAAAAYFOb9SN1//fG+1V1ZpJ/M5eJAAAAANjUZj1p+CPdk+SvjhwEAAAAgK1h1nM4vStJT3efkuT8\nJJ+Y11AAAAAAbF6znsPp9g23H0ry/u7+7TnMAwAAAMAmN2tw+mCS/6+7H06SqtpWVd/Q3X86v9EA\nAAAA2IxmPYfTLUlO3nD/5CS/Pn4cAAAAADa7WYPTM7r7y8fuTLe/YT4jAQAAALCZzRqcvlJVLzh2\np6ouSPLAfEYCAAAAYDOb9RxOb07y76vqvyWpJH8xyd+Z21QAAAAAbFozBafu/nhV/ZUkz50O3d3d\nX53fWAAAAABsVjN9pK6qLk2yvbvv7O47k+yoqjfOdzQAAAAANqNZz+H0+u7+42N3uvtLSV4/n5EA\nAAAA2MxmDU7bqqqO3amqbUmeNp+RAAAAANjMZj1p+EeT/HJV/fx0/0eT/Op8RgIAAABgM5s1OP2z\nHP0I3bHzNn00yVVzmQgAAACATe0xg1NVnZTkXyb54SRfmA7/pSSfz9GP4z081+kAAAAA2HQe7xxO\nP5Xkm5J8W3e/oLtfkOTsJKck+el5DwcAAADA5vN4wenlOXqFuj85dmC6/feTvGyegwEAAACwOT1e\ncOru7uMcfDjJ1x0HAAAAgMcLTp+qqtc88mBV/d0kn5nPSAAAAABsZo93lbpLk/xKVb0uyb7p2FqS\nk5P84DwHAwAAAGBzeszg1N2Hkrywqr47yfOmwzd29y1znwwAAACATenx3uGUJOnu30jyG3OeBQAA\nAIAt4PHO4QQAAAAAT4jgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABD\nCU4AAAAADCU4AQAAADCU4AQAAADAUAsPTlX13Kq6Y8PX/VX15qp6W1Ud2nD8ZRue85aqOlBVd1fV\n9y96ZgAAAABmd9Kif2B3353k/CSpqm1JDiX5cJIfTvIz3f3TGx9fVecmuSjJ85J8S5Jfr6pv7+6H\nFzo4AAAAADNZ9kfqXpLkc939B4/xmFck2dvdD3b37yc5kOTChUwHAAAAwBO27OB0UZL3b7j/pqr6\nZFVdXVXPno6dnuQLGx5zz3QMAAAAgBVU3b2cH1z1tCT/LcnzuvveqtqZ5A+TdJKfTHJad7+uqn42\nyW3d/YvT865KclN3f/A4r7knyZ4k2blz5wV79+5d0G8zP4fvO5J7H1j2FCeW804/ZdkjnFD2Hzoy\n5HV2nhx7ZQbW92KNWt8jbeW9Yn0v3iqu8VFWca9Y44u1ldf3SKP2ivW9eNb4Yp19yrbs2LFj2WMM\nsWvXrn3dvfZ4j1v4OZw2eGmST3T3vUly7M8kqapfSHLDdPdQkjM3PO+M6djX6e4rk1yZJGtra72+\nvj5+6gV717XX5Yr9y/xrOvEcfNX6skc4oVxy+UeGvM5l5z1kr8zA+l6sUet7pK28V6zvxVvFNT7K\nKu4Va3yxtvL6HmnUXrG+F88aX6xrdm/PVmgUT8QyP1J3cTZ8nK6qTtvwvR9Mcud0+/okF1XV06vq\n7CTnJPmdhU0JAAAAwBOylH+2qartSb43yRs2HP5XVXV+jn6k7uCx73X3XVX1gSSfSvJQkktdoQ4A\nAABgdS0lOHX3V5J88yOOvfoxHv/2JG+f91wAAAAAPHnLvkodAAAAAFuM4AQAAADAUIITAAAAAEMJ\nTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABD\nCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAA\nQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAA\nAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAA\nAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMA\nAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIIT\nAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCC\nEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQ\nSwtOVXWwqvZX1R1Vdft07Juq6uaq+uz057On41VV76yqA1X1yap6wbLmBgAAAOCxLfsdTru6+/zu\nXpvuX57klu4+J8kt0/0keWmSc6avPUnevfBJAQAAAJjJsoPTI70iyXun2+9N8soNx9/XR92W5FlV\nddoyBgQAAADgsS0zOHWSX6uqfVW1Zzq2s7u/ON3+70l2TrdPT/KFDc+9ZzoGAAAAwIqp7l7OD646\nvbsPVdVfSHJzkn+Q5PruftaGx3ypu59dVTckeUd3/9Z0/JYkP9Hdtz/iNffk6EfusnPnzgv27t27\nqF9nbg7fdyT3PrDsKU4s551+yrJHOKHsP3RkyOvsPDn2ygys78Uatb5H2sp7xfpevFVc46Os4l6x\nxhdrK6/vkUbtFet78azxxTr7lG3ZsWPHsscYYteuXfs2nBrpUZ20iGGOp7sPTX8erqoPJ7kwyb1V\ndVp3f3H6yNzh6eGHkpy54elnTMce+ZpXJrkySdbW1np9fX2Ov8FivOva63LF/qX9NZ2QDr5qfdkj\nnFAuufwjQ17nsvMesldmYH0v1qj1PdJW3ivW9+Kt4hofZRX3ijW+WFt5fY80aq9Y34tnjS/WNbu3\nZys0iidiKR+pq6rtVfWNx24n+b4kdya5Pslrp4e9Nsl10+3rk7xmulrdi5Ic2fDROwAAAABWyLL+\n2WZnkg9X1bEZfqm7f7WqPp7kA1X1I0n+IMnfnh5/Y5KXJTmQ5E+T/PDiRwYAAABgFksJTt39+ST/\n53GO/1GSlxzneCe5dAGjAQAAAPAkLfMqdQAAAABsQYITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAA\nAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQA\nAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAE\nAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTg\nBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU\n4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAw\nlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAA\nMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAA\nADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAy18OBU\nVWdW1W9W1aeq6q6q+rHp+Nuq6lBV3TF9vWzDc95SVQeq6u6q+v5FzwwAAADA7E5aws98KMll3f2J\nqvrGJPuq6ubpez/T3T+98cFVdW6Si5I8L8m3JPn1qvr27n54oVMDAAAAMJOFv8Opu7/Y3Z+Ybv9J\nkk8nOf0xnvKKJHu7+8Hu/v0kB5JcOP9JAQAAAPjfUd29vB9edVaSjyV5fpIfT3JJkvuT3J6j74L6\nUlX9bJLbuvsXp+dcleSm7v7gcV5vT5I9SbJz584L9u7du4DfYr4O33ck9z6w7ClOLOedfsqyRzih\n7D90ZMjSVGwGAAAKrElEQVTr7Dw59soMrO/FGrW+R9rKe8X6XrxVXOOjrOJescYXayuv75FG7RXr\ne/Gs8cU6+5Rt2bFjx7LHGGLXrl37unvt8R63jI/UJUmqakeSDyV5c3ffX1XvTvKTSXr684okr3si\nr9ndVya5MknW1tZ6fX196MzL8K5rr8sV+5f213RCOviq9WWPcEK55PKPDHmdy857yF6ZgfW9WKPW\n90hbea9Y34u3imt8lFXcK9b4Ym3l9T3SqL1ifS+eNb5Y1+zenq3QKJ6IpVylrqqemqOx6dru/pUk\n6e57u/vh7v5akl/In31s7lCSMzc8/YzpGAAAAAAraBlXqaskVyX5dHf/6w3HT9vwsB9Mcud0+/ok\nF1XV06vq7CTnJPmdRc0LAAAAwBOzjPcJf2eSVyfZX1V3TMf+SZKLq+r8HP1I3cEkb0iS7r6rqj6Q\n5FM5eoW7S12hDgAAAGB1LTw4dfdvJanjfOvGx3jO25O8fW5DAQAAADDMUs7hBAAAAMDWJTgBAAAA\nMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAA\nADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEA\nAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgB\nAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4\nAQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwl\nOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAADCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAM\nJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAAAAwlOAEAAAAwlOAEAAAAwFCCEwAAAABDCU4AAAAA\nDCU4AQAAADCU4AQAAADAUIITAAAAAEMJTgAAAAAMJTgBAAAAMJTgBAAAAMBQghMAAAAAQwlOAAAA\nAAwlOAEAAAAw1KYJTlW1u6rurqoDVXX5sucBAAAA4Pg2RXCqqm1Jfi7JS5Ocm+Tiqjp3uVMBAAAA\ncDybIjgluTDJge7+fHf/zyR7k7xiyTMBAAAAcBybJTidnuQLG+7fMx0DAAAAYMVUdy97hsdVVT+U\nZHd3/73p/quTvLC73/SIx+1Jsme6+9wkdy900Pk4NckfLnsI2ATsFZiNvQKzsVdgNvYKzGYr7ZVv\n7e7nPN6DTlrEJAMcSnLmhvtnTMf+nO6+MsmVixpqEarq9u5eW/YcsOrsFZiNvQKzsVdgNvYKzOZE\n3Cub5SN1H09yTlWdXVVPS3JRkuuXPBMAAAAAx7Ep3uHU3Q9V1ZuSfDTJtiRXd/ddSx4LAAAAgOPY\nFMEpSbr7xiQ3LnuOJdhSHxGEObJXYDb2CszGXoHZ2CswmxNur2yKk4YDAAAAsHlslnM4AQAAALBJ\nCE4rqqqurqrDVXXnsmeBVVZVZ1bVb1bVp6rqrqr6sWXPBKuoqp5RVb9TVf912iv/z7JnglVVVduq\n6ner6oZlzwKrrKoOVtX+qrqjqm5f9jywiqrqWVX1war6TFV9uqr+r2XPtCg+UreiqurFSb6c5H3d\n/fxlzwOrqqpOS3Jad3+iqr4xyb4kr+zuTy15NFgpVVVJtnf3l6vqqUl+K8mPdfdtSx4NVk5V/XiS\ntSTP7O6XL3seWFVVdTDJWnf/4bJngVVVVe9N8p+6+z1V9bQk39Ddf7zsuRbBO5xWVHd/LMl9y54D\nVl13f7G7PzHd/pMkn05y+nKngtXTR315uvvU6cu/OsEjVNUZSX4gyXuWPQsAm1tVnZLkxUmuSpLu\n/p8nSmxKBCdgC6mqs5J8R5L/stxJYDVNHxO6I8nhJDd3t70CX+/fJPnHSb627EFgE+gkv1ZV+6pq\nz7KHgRV0dpL/keT/nT6q/Z6q2r7soRZFcAK2hKrakeRDSd7c3fcvex5YRd39cHefn+SMJBdWlY9s\nwwZV9fIkh7t737JngU3ir3X3C5K8NMml02lBgD9zUpIXJHl3d39Hkq8kuXy5Iy2O4ARsetP5aD6U\n5Nru/pVlzwOrbnor928m2b3sWWDFfGeSvzGdl2Zvku+uql9c7kiwurr70PTn4SQfTnLhcieClXNP\nkns2vKv8gzkaoE4IghOwqU0nQr4qyae7+18vex5YVVX1nKp61nT75CTfm+Qzy50KVkt3v6W7z+ju\ns5JclOQ3uvvvLnksWElVtX26YEumjwh9XxJX2IYNuvu/J/lCVT13OvSSJCfMxY1OWvYAHF9VvT/J\nepJTq+qeJG/t7quWOxWspO9M8uok+6dz0yTJP+nuG5c4E6yi05K8t6q25eg/OH2gu13yHYD/XTuT\nfPjov/3lpCS/1N2/utyRYCX9gyTXTleo+3ySH17yPAtT3S5QAwAAAMA4PlIHAAAAwFCCEwAAAABD\nCU4AAAAADCU4AQAAADCU4AQAAADAUIITAHDCq6qHq+qOqrqrqv5rVV1WVU+ZvrdWVe8c8DOuqapD\nVfX06f6pVXXwyb7u9FrrVXXDiNcC4P9v535CrCrDOI5/fyiVOIhCudckTDBkFiLkJpRWrfpjuQjE\nRQTWInFZRFCIOxcDustVVi6iYBY14kbDqGHKf4hI/3Q3IRFDlJA+Le6ZOHPVmXtvB4z4fjbnvOec\n+7zPvavLc573ldSF5fc7AUmSpP+AP6pqC0CStcAHwCrg7aqaBqY7mucWsBc40lG8TiRZVlW37nce\nkiTp/8MOJ0mSpJaqmgVeAV5Lzz/dQ0nGkryf5EKS80mea64/neRskpkkJ5KM3SP8YeCNJAte+vV3\nKCWZSLKnOf8pycGmA2s6yXiSz5N8n+TVVphVSSaTXElytNWhddfcmriHkswAL3Ty40mSJDUsOEmS\nJPWpqh+AZcDavltvAb9V1eaqegI4leRh4E1gZ1WN0+uG2n+P0NeAM8DLQ6Z0renAOg0cA54HtgHv\ntJ7ZCrwObAIeBZ4dILcbVTVeVR8OmY8kSdKiXFInSZI0uJ3AS/ODqvo1yTP0ijxfJgF4ADi7SIyD\nwKfA5BDzftYcLwBjVTUHzCW5mWR1c+/rplBGkuPAduDPJXL7aIgcJEmSBmbBSZIkqU+S9fT2W5oF\nHl/qcWCqqnYPEruqrib5DtjVuvwXCzvPH+r72M3meLt1Pj+e/z9X/VMNkNvvg+QsSZI0LJfUSZIk\ntSR5BDgKTFRVfxFnCtjXenYN8BXwZJINzbWVSR5bYpr3gAOt8c/ApiQPNh1LO0ZIfWuSdc3eTS/S\nW7o3Sm6SJEn/mgUnSZIkWNFsyn0JOAl8wcL9kea9C6xJcjHJOeCpqvoF2AMcT3Ke3pK1jYtNVlWX\ngJnW+DrwMXCxOX47wnf4BpgALgM/Ap+MkpskSVIXcueLO0mSJEmSJGl0djhJkiRJkiSpUxacJEmS\nJEmS1CkLTpIkSZIkSeqUBSdJkiRJkiR1yoKTJEmSJEmSOmXBSZIkSZIkSZ2y4CRJkiRJkqROWXCS\nJEmSJElSp/4GZuC9GNWuBlIAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize = (20,10))\n",
+ "plt.hist(series,bins = 11,align = 'mid')\n",
+ "plt.xlabel('Dice Number')\n",
+ "plt.ylabel('Occurences')\n",
+ "plt.grid()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.4956\n",
+ "3.5103\n"
+ ]
+ }
+ ],
+ "source": [
+ "print len([x for x in series if x <= 3])/float(len(series))\n",
+ "print np.mean(series)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.4956\n",
+ "3.5103\n"
+ ]
+ }
+ ],
+ "source": [
+ "print len([x for x in series if x <= 3])/float(len(series))\n",
+ "print np.mean(series)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "def trial():\n",
+ " number = [1,2,3,4,5,6,7,8,9,10]\n",
+ " a = random.choice(number)\n",
+ " if a<= 7:\n",
+ " return 1\n",
+ " else:\n",
+ " return 0"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "7\n"
+ ]
+ }
+ ],
+ "source": [
+ "res = [trial() for x in range(10)]\n",
+ "print sum(res)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.2367\n"
+ ]
+ }
+ ],
+ "source": [
+ "def binomial(number):\n",
+ " l = []\n",
+ " for i in range(10000):\n",
+ " res = [trial() for x in range(10)]\n",
+ " l.append(sum(res))\n",
+ " return len([x for x in l if x == number])/float(len(l))\n",
+ " \n",
+ "print binomial(8)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "1 0.0002\n",
+ "2 0.0013\n",
+ "3 0.0087\n",
+ "4 0.0373\n",
+ "5 0.1041\n",
+ "6 0.2000\n",
+ "7 0.2674\n",
+ "8 0.2342\n",
+ "9 0.1153\n",
+ "10 0.0283\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "prob = []\n",
+ "for i in range(1,11):\n",
+ " prob.append(binomial(i))\n",
+ "prob_s = pd.Series(prob,index = range(1,11))\n",
+ "print prob_s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.266827932\n",
+ "0.2334744405\n"
+ ]
+ }
+ ],
+ "source": [
+ "print (float(factorial(10))/(factorial(7)*factorial(10-7)))*(0.7**7)*(0.3**3)\n",
+ "print (float(factorial(10))/(factorial(8)*factorial(10-8)))*(0.7**8)*(0.3**2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABIsAAAJCCAYAAABAuEcoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHp5JREFUeJzt3X+s3fdd3/HXe/FaSiNlgSJrJFEdRGCEeWtXk7BVa531\nB2aZEv4oIqhUidQq2kQ2NoImI7R2CtMUfnTaNFVbIwhUwDAQEFgkrOva3u0PVpak7ZomXVQ3eK09\naIF0AZesxfS9P+7hze2dm3tjX/vcYz8ekuXz/Z7v9+R99e2nPX3me86t7g4AAAAAJMlfWPYAAAAA\nAOweYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABh7\nlj3AZi95yUt63759yx4DdoXPfe5zefGLX7zsMWDlWDtwdqwdODvWDpwda+fCevTRR3+/u79mO8fu\nuli0b9++PPLII8seA3aFtbW1HDx4cNljwMqxduDsWDtwdqwdODvWzoVVVf9ru8f6GBoAAAAAQywC\nAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABg\niEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAA\nAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYe5Y9AAAALNO+ww8ue4SLxvF7b172\nCADsAHcWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACA\nIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEA\nAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDE\nIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAGNbsaiqDlXVk1V1rKoOn+H576+qJ6rqI1X13qp66Ybn\n/rSqPrz4c3QnhwcAAABgZ+3Z6oCquizJO5K8LsmJJA9X1dHufmLDYR9KcqC7/7iq/kGSH03yXYvn\nnu3ul+3w3AAAAACcB9u5s+iGJMe6+6nu/kKSI0lu3XhAd7+/u/94sfmBJFfv7JgAAAAAXAjbiUVX\nJfnUhu0Ti31fzpuT/MaG7a+oqkeq6gNV9R1nMSMAAAAAF8iWH0N7Pqrqe5IcSPLqDbtf2t0nq+rr\nkryvqh7r7k9sOu/OJHcmyd69e7O2traTY8HKOnXqlPUAZ8HagbNzqa6du/efXvYIF41L8T8/yaW7\nduBcWTu713Zi0ckk12zYvnqx70tU1WuT/FCSV3f35/9sf3efXPz9VFWtJXl5ki+JRd19X5L7kuTA\ngQN98ODB5/VDwMVqbW0t1gM8f9YOnJ1Lde3ccfjBZY9w0Tj+xoPLHmEpLtW1A+fK2tm9tvMxtIeT\nXFdV11bVC5LcluRLfqtZVb08yTuT3NLdn9mw/8qqeuHi8UuSvDLJxi/GBgAAAGAX2fLOou4+XVV3\nJXl3ksuS3N/dj1fVPUke6e6jSX4syeVJfqmqkuST3X1Lkm9K8s6q+mLWw9S9m36LGgAAAAC7yLa+\ns6i7H0ry0KZ9b93w+LVf5rzfTLL/XAYEAAAA4MLZzsfQAAAAALhEiEUAAAAADLEIAAAAgCEWAQAA\nADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQi\nAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAA\nhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABg7Fn2AAAAAF/OvsMPLnuELd29/3TuWIE5j99787JH\nAFaEO4sAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQ\niwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAA\nABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIR\nAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAA\nQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIA\nAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCI\nRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAA\nAAyxCAAAAIAhFgEAAAAwthWLqupQVT1ZVceq6vAZnv/+qnqiqj5SVe+tqpdueO72qvr44s/tOzk8\nAAAAADtry1hUVZcleUeSb09yfZLvrqrrNx32oSQHuvuvJXkgyY8uzv2qJG9LcmOSG5K8raqu3Lnx\nAQAAANhJ27mz6IYkx7r7qe7+QpIjSW7deEB3v7+7/3ix+YEkVy8ef1uS93T309392STvSXJoZ0YH\nAAAAYKdtJxZdleRTG7ZPLPZ9OW9O8htneS4AAAAAS7RnJ1+sqr4nyYEkr36e592Z5M4k2bt3b9bW\n1nZyLFhZp06dsh7gLFg77EaPnXxm2SNsae+Lkn/7c7+27DG2tP+qK3b09e7ef3pHX+9Sdj7+u3cV\nrs/eF63GnP63kd3Ge7bdazux6GSSazZsX73Y9yWq6rVJfijJq7v78xvOPbjp3LXN53b3fUnuS5ID\nBw70wYMHNx8Cl6S1tbVYD/D8WTvsRnccfnDZI2zp7v2n8/bHdvTfJZ4Xx994cEdfbxWuzarY6WuT\nrMb1uVTXDpwr79l2r+18DO3hJNdV1bVV9YIktyU5uvGAqnp5kncmuaW7P7PhqXcneX1VXbn4YuvX\nL/YBAAAAsAttmb+7+3RV3ZX1yHNZkvu7+/GquifJI919NMmPJbk8yS9VVZJ8srtv6e6nq+qHsx6c\nkuSe7n76vPwkAAAAAJyzbd0r2d0PJXlo0763bnj82uc49/4k95/tgAAAAABcONv5GBoAAAAAlwix\nCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAA\ngCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYB\nAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAw\nxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAA\nAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZY\nBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAA\nwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsA\nAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAY\nYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAA\nAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMs\nAgAAAGBsKxZV1aGqerKqjlXV4TM8/6qq+mBVna6qN2x67k+r6sOLP0d3anAAAAAAdt6erQ6oqsuS\nvCPJ65KcSPJwVR3t7ic2HPbJJHck+YEzvMSz3f2yHZgVAAAAgPNsy1iU5IYkx7r7qSSpqiNJbk0y\nsai7jy+e++J5mBEAAACAC6S6+7kPWP9Y2aHufsti+01Jbuzuu85w7E8n+fXufmDDvtNJPpzkdJJ7\nu/tXz3DenUnuTJK9e/e+4siRI2f9A8HF5NSpU7n88suXPQasHGuH3eixk88se4Qt7X1R8ulnlz3F\n1vZfdcWOvt4qXJtVsdPXJlmN63Oprh04V96zXVg33XTTo919YDvHbufOonP10u4+WVVfl+R9VfVY\nd39i4wHdfV+S+5LkwIEDffDgwQswFux+a2trsR7g+bN22I3uOPzgskfY0t37T+ftj12It4fn5vgb\nD+7o663CtVkVO31tktW4Ppfq2oFz5T3b7rWdL7g+meSaDdtXL/ZtS3efXPz9VJK1JC9/HvMBAAAA\ncAFtJxY9nOS6qrq2ql6Q5LYk2/qtZlV1ZVW9cPH4JUlemQ3fdQQAAADA7rJlLOru00nuSvLuJB9L\n8ovd/XhV3VNVtyRJVX1LVZ1I8p1J3llVjy9O/6Ykj1TV/0jy/qx/Z5FYBAAAALBLbeuDtd39UJKH\nNu1764bHD2f942mbz/vNJPvPcUYAAAAALpDtfAwNAAAAgEuEWAQAAADAEIsAAAAAGGIRAAAAAEMs\nAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAA\nYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUA\nAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAM\nsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAA\nAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEW\nAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAA\nMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAIw9yx4AAACA1bPv8IPLHuGi\ncfzem5c9AnwJdxYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyx\nCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAA\ngCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGHuWPQAAsDP2HX5w2SNcNI7fe/OyRwAAWBp3FgEA\nAAAwxCIAAAAAhlgEAAAAwBCLAAAAABjbikVVdaiqnqyqY1V1+AzPv6qqPlhVp6vqDZueu72qPr74\nc/tODQ4AAADAztsyFlXVZUnekeTbk1yf5Lur6vpNh30yyR1J/sOmc78qyduS3JjkhiRvq6orz31s\nAAAAAM6H7dxZdEOSY939VHd/IcmRJLduPKC7j3f3R5J8cdO535bkPd39dHd/Nsl7khzagbkBAAAA\nOA+qu5/7gPWPlR3q7rcstt+U5MbuvusMx/50kl/v7gcW2z+Q5Cu6+18stv9Zkme7+8c3nXdnkjuT\nZO/eva84cuTIuf5ccFE4depULr/88mWPASvnUl07j518ZtkjXDT2X3XFjr/mKlyfvS9KPv3ssqfY\n2k5fn1W4NqvC2tndrJ3d63ysnVVwqb5nW5abbrrp0e4+sJ1j95zvYbaju+9Lcl+SHDhwoA8ePLjc\ngWCXWFtbi/UAz9+lunbuOPzgske4aBx/48Edf81VuD537z+dtz+2K94ePqedvj6rcG1WhbWzu1k7\nu9f5WDur4FJ9z7YKtvMxtJNJrtmwffVi33acy7kAAAAAXGDbiUUPJ7muqq6tqhckuS3J0W2+/ruT\nvL6qrlx8sfXrF/sAAAAA2IW2jEXdfTrJXVmPPB9L8ovd/XhV3VNVtyRJVX1LVZ1I8p1J3llVjy/O\nfTrJD2c9OD2c5J7FPgAAAAB2oW19sLa7H0ry0KZ9b93w+OGsf8TsTOfen+T+c5gRAAAAgAtkOx9D\nAwAAAOASIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAA\nAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEW\nAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAA\nMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIA\nAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACG\nWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAA\nAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCL\nAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAA\nGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEA\nAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABD\nLAIAAABgbCsWVdWhqnqyqo5V1eEzPP/CqvqFxfO/VVX7Fvv3VdWzVfXhxZ9/v7PjAwAAALCT9mx1\nQFVdluQdSV6X5ESSh6vqaHc/seGwNyf5bHd/fVXdluRHknzX4rlPdPfLdnhuAAAAAM6D7dxZdEOS\nY939VHd/IcmRJLduOubWJO9aPH4gyWuqqnZuTAAAAAAuhO3EoquSfGrD9onFvjMe092nkzyT5KsX\nz11bVR+qqv9SVX/7HOcFAAAA4Dyq7n7uA6rekORQd79lsf2mJDd2910bjvno4pgTi+1PJLkxyR8l\nuby7/6CqXpHkV5N8c3f/4aZ/xp1J7kySvXv3vuLIkSM79fPBSjt16lQuv/zyZY8BK+dSXTuPnXxm\n2SNcNPZfdcWOv+YqXJ+9L0o+/eyyp9jaTl+fVbg2q8La2d2snd3rfKydVXCpvmdblptuuunR7j6w\nnWO3/M6iJCeTXLNh++rFvjMdc6Kq9iS5Iskf9HqJ+nySdPeji4j0DUke2Xhyd9+X5L4kOXDgQB88\neHA7s8NFb21tLdYDPH+X6tq54/CDyx7honH8jQd3/DVX4frcvf903v7Ydt4eLtdOX59VuDarwtrZ\n3ayd3et8rJ1VcKm+Z1sF2/kY2sNJrquqa6vqBUluS3J00zFHk9y+ePyGJO/r7q6qr1l8QXaq6uuS\nXJfkqZ0ZHQAAAICdtmX+7u7TVXVXkncnuSzJ/d39eFXdk+SR7j6a5CeT/ExVHUvydNaDUpK8Ksk9\nVfUnSb6Y5O9399Pn4wcBAAAA4Nxt617J7n4oyUOb9r11w+P/m+Q7z3DeLyf55XOcEQAAAIALZDsf\nQwMAAADgEiEWAQAAADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgA\nAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAh\nFgEAAAAwxCIAAAAAhlgEAAAAwNiz7AEAWC37Dj+47BG2dPf+07ljBeY8fu/Nyx4BAAD+P+4sAgAA\nAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhF\nAAAAAAyxCAAAAIAhFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABjz7IHAAAAAHbWvsMP\nLnuELd29/3TuWIE5j99787JHuODcWQQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgA\nAACAIRYBAAAAMMQiAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAAyxCAAAAIAh\nFgEAAAAwxCIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAA\nADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAEMsAgAAAGCIRQAAAAAMsQgAAACAIRYBAAAAMMQi\nAAAAAIZYBAAAAMAQiwAAAAAYYhEAAAAAQywCAAAAYIhFAAAAAIw9yx4AYLN9hx9c9ggXjeP33rzs\nEQAAgBXjziIAAAAAhlgEAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAA\nADDEIgAAAACGWAQAAADAEIsAAAAAGGIRAAAAAGNbsaiqDlXVk1V1rKoOn+H5F1bVLyye/62q2rfh\nuR9c7H+yqr5t50YHAAAAYKft2eqAqrosyTuSvC7JiSQPV9XR7n5iw2FvTvLZ7v76qrotyY8k+a6q\nuj7JbUm+OcnXJvnPVfUN3f2nO/2DwPO17/CDyx5hS3fvP507VmDO4/fevOwRAAAA2CHbubPohiTH\nuvup7v5CkiNJbt10zK1J3rV4/ECS11RVLfYf6e7Pd/dvJzm2eD0AAAAAdqEt7yxKclWST23YPpHk\nxi93THefrqpnknz1Yv8HNp171VlPu2JW4c6VVeHOFQAAALgwqruf+4CqNyQ51N1vWWy/KcmN3X3X\nhmM+ujjmxGL7E1kPSv88yQe6+2cX+38yyW909wOb/hl3JrlzsfmNSZ489x8NLgovSfL7yx4CVpC1\nA2fH2oGzY+3A2bF2LqyXdvfXbOfA7dxZdDLJNRu2r17sO9MxJ6pqT5IrkvzBNs9Nd9+X5L7tDAyX\nkqp6pLsPLHsOWDXWDpwdawfOjrUDZ8fa2b22851FDye5rqquraoXZP0Lq49uOuZoktsXj9+Q5H29\nfsvS0SS3LX5b2rVJrkvy33dmdAAAAAB22pZ3Fi2+g+iuJO9OclmS+7v78aq6J8kj3X00yU8m+Zmq\nOpbk6awHpSyO+8UkTyQ5neR7/SY0AAAAgN1ry+8sApanqu5cfEwTeB6sHTg71g6cHWsHzo61s3uJ\nRQAAAACM7XxnEQAAAACXCLEIdqGquqaq3l9VT1TV41X1fcueCVZFVV1WVR+qql9f9iywSqrqL1XV\nA1X1P6vqY1X1N5c9E6yCqvoni/drH62qn6+qr1j2TLAbVdX9VfWZqvrohn1fVVXvqaqPL/6+cpkz\n8ufEItidTie5u7uvT/KtSb63qq5f8kywKr4vyceWPQSsoH+T5D92919J8tdjHcGWquqqJP8oyYHu\n/qtZ/4VAty13Kti1fjrJoU37Did5b3dfl+S9i212AbEIdqHu/p3u/uDi8R9l/Q37VcudCna/qro6\nyc1JfmLZs8Aqqaorkrwq67/hNt39he7+P8udClbGniQvqqo9Sb4yyf9e8jywK3X3f836b0/f6NYk\n71o8fleS77igQ/FliUWwy1XVviQvT/Jby50EVsK/TvJPk3xx2YPAirk2ye8l+anFxzh/oqpevOyh\nYLfr7pNJfjzJJ5P8TpJnuvs/LXcqWCl7u/t3Fo9/N8neZQ7DnxOLYBerqsuT/HKSf9zdf7jseWA3\nq6q/l+Qz3f3osmeBFbQnyd9I8u+6++VJPhcfBYAtLb5f5dasB9evTfLiqvqe5U4Fq6nXf1W7X9e+\nS4hFsEtV1V/Meij6ue7+lWXPAyvglUluqarjSY4k+TtV9bPLHQlWxokkJ7r7z+5ifSDr8Qh4bq9N\n8tvd/Xvd/SdJfiXJ31ryTLBKPl1VfzlJFn9/ZsnzsCAWwS5UVZX17434WHf/q2XPA6ugu3+wu6/u\n7n1Z/3LR93W3f7sL29Ddv5vkU1X1jYtdr0nyxBJHglXxySTfWlVfuXj/9pr4cnh4Po4muX3x+PYk\nv7bEWdhALILd6ZVJ3pT1OyM+vPjzd5c9FAAXtX+Y5Oeq6iNJXpbkXy55Htj1FnfjPZDkg0key/r/\nv7pvqUPBLlVVP5/kvyX5xqo6UVVvTnJvktdV1cezfqfevcuckT9X6x8LBAAAAAB3FgEAAACwgVgE\nAAAAwBCLAAAAABhiEQAAAABDLAIAAABgiEUAAAAADLEIAAAAgCEWAQAAADD+Hw8MfyQd2qMyAAAA\nAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize = (20,10))\n",
+ "plt.bar(range(1,11),prob)\n",
+ "plt.grid()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABJkAAAJCCAYAAABj4xb9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl0XPd55vnnLexLVQEgAGIlQUpcAJAESJGUbFlOx5sk\n2yM5u+xx4u6TjONuazrHmcmJsxxPxt3pybhnPJ6ecXfbSft0lnYUJ25n5LYcyfKqxTJXQCQAUtxZ\nAAESW6FA7ED95g8UFIjmgqUubi3fzzk8Yt2qCzzy8R91Hv3e95pzTgAAAAAAAMB6BPwOAAAAAAAA\ngPRHyQQAAAAAAIB1o2QCAAAAAADAulEyAQAAAAAAYN0omQAAAAAAALBulEwAAAAAAABYN0omAAAA\nAAAArBslEwAAAAAAANaNkgkAAAAAAADrlut3gGSprKx0TU1NfscAAAAAAADIGMePHx9yzlWt5LMZ\nUzI1NTXp2LFjfscAAAAAAADIGGZ2ZaWfZVwOAAAAAAAA60bJBAAAAAAAgHWjZAIAAAAAAMC6UTIB\nAAAAAABg3SiZAAAAAAAAsG6UTAAAAAAAAFg3SiYAAAAAAACsGyUTAAAAAAAA1o2SCQAAAAAAAOtG\nyQQAAAAAAIB1o2QCAAAAAADAulEyAQAAAAAAYN0omQAAAAAAALBulEwAAAAAAABYN0omAAAAAAAA\nrBslEwAAAAAAANbN05LJzB4zs7Nmdt7MPn2Xz/2CmTkzO7js2u8l7jtrZo96mRMAAAAAAADrk+vV\nDzazHElflPReSb2SjprZs8657ls+F5T0W5J+suxai6SnJLVKqpP0opntdM4teJUXAAAAAAAAa+fl\nSabDks475y4652YlPSPpydt87l9J+t8lTS+79qSkZ5xzM865S5LOJ34eAAAAAAAAUpCXJVO9pMiy\n172Ja28yswOSGp1z31rtvYn7P25mx8zs2ODgYHJSAwAAAAAAYNV8W/xtZgFJn5f0P631Zzjnvuyc\nO+icO1hVVZW8cAAAAAAAAFgVz3YySeqT1LjsdUPi2pKgpD2SfmBmklQj6Vkze2IF9wIAAAAAACCF\neFkyHZW0w8y2abEgekrSR5bedM6NSapcem1mP5D0PzvnjpnZlKSvmtnntbj4e4ekIx5mBQAA2DA3\nxqf1Zy9d0pFLI8oNmB7cXqFffahJNeFCv6MBAACsmWfjcs65eUlPS3peUo+krznnuszss4nTSne7\nt0vS1yR1S/oHSZ/kyXIAACATnLw6qse/8JL+08uXVJSXI0n6Dz+4oHf/nz/QX712Rc45nxMCAACs\njWXKF5mDBw+6Y8eO+R0DAADgji4PTeiJ//dllRXn6z997KB2bA5Kkq4MT+gPvnFaL58f0iM7KvX5\nX25XVbDA57QAAACSmR13zh1cyWd9W/wNAACQTeYX4nr6r08oEDD9l9948M2CSZK2birRX/76Yf3r\nD+3RkUsjev+/e0mvXhjyMS0AAMDqUTIBAABsgL987YpO98X0b35urxorin/qfTPTRx/aqr//5MMK\nFubqo3/2E/27757TQjwzTp0DAIDMR8kEAADgsdj0nL7w4jk9sqNSj++puetnm2tD+ubT79CT7fX6\n/Hfe0Ef/7CeKjExuUFIAAIC1o2QCAADw2J+/clljU3P63cd2y8zu+fmSglx9/pfb9Llf2KdTfWN6\n9As/0n9+5ZLinGoCAAApjJIJAADAQ9NzC/rKK5f07t3V2lMfXvF9ZqZfPtSo5z/1Th1qqtAffbNb\nv/LlH+vi4E0P0wIAAKwdJRMAAICH/r+OPo1Ozuk3Htm+pvvry4r0n//ZIf0fv9SmswPj+uD/87K+\n0309ySkBAADWj5IJAADAQ3/x4yvaXRPUQ9sr1vwzzEy/+ECDXvjUz2hHdal+8y+P6Zud15KYEgAA\nYP0omQAAADzSfS2mrmsxffjwlhXtYrqXmnCh/vrjD+lgU4U+9Tcdeu3icBJSAgAAJAclEwAAgEe+\ncbJXeTmmJ9rqkvYzi/Nz9ae/dlBbNhXrX/yXE7oxPp20nw0AALAelEwAAAAemF+I6+87ruldu6tV\nXpKf1J8dLsrTl3/1AU3MzOv3vn5KzvHUOQAA4D9KJgAAAA+8fH5Ig+Mz+vkDDZ78/Purg/qdR3fp\nu2du6HtnbnjyOwAAAFaDkgkAAMADXz/Rp7LiPP3srmrPfsfH3t6k7ZUl+uPnejS3EPfs9wAAAKwE\nJRMAAECSTc0u6DvdA/rgvlrl53r3dSsvJ6Dff3+zLg5O6Ks/uerZ7wEAAFgJSiYAAIAk++Ebg5qe\ni+vxPbWe/653N1fr7fdt0v/14hu6OTPv+e8DAAC4E0omAACAJHuha0BlxXk6vK3C899lZvqdR3cp\nOjmnZ45wmgkAAPiHkgkAACCJ5hbierHnut69e7Pycjbmq9b+LeV6aHuF/uylS5qdZzcTAADwByUT\nAABAEv3k4ohi0/N6tHXzhv7ef/5P7tdAbFp/39G3ob8XAABgCSUTAABAEj3fNaCivBy9c2fVhv7e\nd+6oVEttSP/xhxcUj7sN/d0AAAASJRMAAEDSxONOL3QP6Gd2VqkwL2dDf7eZ6Td/ZrsuDk7oR+cG\nN/R3AwAASJRMAAAASdPZG9X12Iwe3bOxo3JLHt9Tq8rSAv3Fj6/48vsBAEB2o2QCAABIkue7ris3\nYHrXLn9KpvzcgD5yuFHfP3tDkZFJXzIAAIDsRckEAACQBM45Pd81oLfdt0nh4jzfcnzkwa0KmOmv\nXuM0EwAA2FiUTAAAAElw7sZNXRqa0KOtNb7mqAkX6n0tm/U3xyKanlvwNQsAAMgulEwAAABJ8Pzp\nAZlJ72vxZ1RuuV97W5Oik3N6tvOa31EAAEAWoWQCAABIgue7B7S/sUzVoUK/o+ih7RXaublUf/Hj\ny3LO+R0HAABkCUomAACAdeodndTpvpjvo3JLzEy/+tBWne6L6fXeMb/jAACALEHJBAAAsE4vdF2X\npJQpmSTpyf31KsrL0TNHr/odBQAAZAlKJgAAgHV6vmtAuzYH1VRZ4neUN4UK8/SBfbV6tuOaJmbm\n/Y4DAACyACUTAADAOgzfnNHRyyN6tNX/hd+3+vDhRk3MLuibLAAHAAAbgJIJAABgHV7ovq64kx7b\nU+t3lJ9yYEu5dlSX6q+PRvyOAgAAsgAlEwAAwDp8+/SAtm4qVnNt0O8oP8XM9NThLeqMRNXTH/M7\nDgAAyHCUTAAAAGs0NjmnV88P6bE9NTIzv+Pc1s/vr1d+TkDPHGEBOAAA8BYlEwAAwBq92HNd83Gn\nx1NwVG5JeUm+HttTo2+c7NP03ILfcQAAQAajZAIAAFijb58eUF24UG0NYb+j3NVThxsVm57Xc6f6\n/Y4CAAAyGCUTAADAGtycmdePzg3q0RQelVvytu2b1LSpWM8cYQE4AADwDiUTAADAGnz/zA3Nzsf1\nWGuN31Huycz0K4e26MjlEV0YvOl3HAAAkKEomQAAANbgH04PqLI0XwebKvyOsiK/cKBeAZO+caLP\n7ygAACBDUTIBAACs0vTcgr5/9obe11qjnEBqj8otqQ4V6pEdVfrGyT7F487vOAAAIANRMgEAAKzS\nD98Y1OTsgh7fk/qjcsv9/IF69UWn9NqlYb+jAACADETJBAAAsEr/cHpA4aI8PbR9k99RVuXR1hoF\nC3L1XxmZAwAAHqBkAgAAWIXZ+bhe7Lmu97ZsVl5Oen2VKszL0fv31urbp/o1OTvvdxwAAJBh0uub\nEQAAgM9eOT+k8el5vX9veo3KLfn5A/WamF3Q810DfkcBAAAZhpIJAABgFb51ql/Bwly94/4qv6Os\nyaGmCjVWFDEyBwAAko6SCQAAYIVm5+N6oWtA723ZrPzc9PwaFQiYfm5/g14+P6T+sSm/4wAAgAyS\nnt+OAAAAfPDK+SHFpuf1gb21fkdZl5/bXy/npG+93u93FAAAkEEomQAAAFboW6f6FSzI1Tt2VPod\nZV22VZaotS6k/0bJBAAAkoiSCQAAYAWWj8oV5Ob4HWfdPrCvVh2RqCIjk35HAQAAGYKSCQAAYAVe\nubA4Kvf+NB+VW/LBvXWSpOdOcZoJAAAkByUTAADACjz3+uKo3CM703tUbsmWTcVqawgzMgcAAJKG\nkgkAAOAe5hbieqH7ut6TIaNySz6wr1an+sZ0eWjC7ygAACADUDIBAADcwyvnhzQ2NZcxo3JLPrBv\ncWTuW4zMAQCAJKBkAgAAuIfnTvWrtCBXj6T5U+VuVV9WpANbyhiZAwAASUHJBAAAcBdLo3Lvbdms\nwrzMGZVb8sF9derpj+nC4E2/owAAgDTnaclkZo+Z2VkzO29mn77N+58ws1Nm1mFmL5tZS+J6k5lN\nJa53mNl/9DInAADAnRy9NKLo5Jwe21PjdxRPPL538d/rH04P+JwEAACkO89KJjPLkfRFSY9LapH0\n4aUSaZmvOuf2OufaJX1O0ueXvXfBOdee+PMJr3ICAADczXd6rqsgN5Bxo3JLasNFamsI64Xu635H\nAQAAac7Lk0yHJZ13zl10zs1KekbSk8s/4JyLLXtZIsl5mAcAAGBVnHN6see6Hr6/UsX5uX7H8cz7\nWmvUGYlqYGza7ygAACCNeVky1UuKLHvdm7j2Fmb2STO7oMWTTP9y2VvbzOykmf3QzB7xMCcAAMBt\nvXH9piIjU3pP82a/o3jq0dbFf7/vdDMyBwAA1s73xd/OuS865+6T9LuS/jBxuV/SFufcfkm/Lemr\nZha69V4z+7iZHTOzY4ODgxsXGgAAZIUXexZHyN7dXO1zEm/dXx3U9qoSPd/FyBwAAFg7L0umPkmN\ny143JK7dyTOSPiRJzrkZ59xw4u/HJV2QtPPWG5xzX3bOHXTOHayqqkpacAAAAEn6Tvd1tTWEtTlU\n6HcUz72vpUavXRzW2OSc31EAAECa8rJkOipph5ltM7N8SU9Jenb5B8xsx7KXH5B0LnG9KrE4XGa2\nXdIOSRc9zAoAAPAWg+Mz6uyN6t0ZPiq35NHWzZqPO33vLKeZAADA2nhWMjnn5iU9Lel5ST2Svuac\n6zKzz5rZE4mPPW1mXWbWocWxuI8lrr9T0uuJ638n6RPOuRGvsgIAANzq5fODck561+7MHpVb0tZQ\npupggV5gZA4AAKyRp49Jcc49J+m5W659Ztnff+sO931d0te9zAYAAHA3L70xpIqSfLXU/tRayIwU\nCJje17pZXz/ep+m5BRXm5fgdCQAApBnfF38DAACkmnjc6UfnhvSO+ysVCJjfcTbMo601mppb0Mvn\nhvyOAgAA0hAlEwAAwC3ODIxr6OaM3rkzux4s8uC2TSrJz9H3zt7wOwoAAEhDlEwAAAC3eOncoCTp\nkR2VPifZWPm5AT2yo0rfP3NDzjm/4wAAgDRDyQQAAHCLl84NadfmoDaHCv2OsuHetbta/WPT6ukf\n9zsKAABIM5RMAAAAy0zNLujI5ZGsO8W05J/sXhwR/D4jcwAAYJUomQAAAJY5fmVUs/NxvSNLS6bq\nYKH2NYT1vTOUTAAAYHUomQAAAJZ57eKwcgKmQ00Vfkfxzc/uqtbJq6MamZj1OwoAAEgjlEwAAADL\nvHZxWHvrwyopyPU7im/etbtacSf98A1OMwEAgJWjZAIAAEiYml1QZ29UD23f5HcUX+2tD6uytEDf\nOzPodxQAAJBGKJkAAAASTlwd1dyC00Pbs3dUTpICAdPP7qrSD8/e0PxC3O84AAAgTVAyAQAAJCzt\nYzqYxfuYlrxrd7Vi0/M6cTXqdxQAAJAmKJkAAAASXrs4rD31YZVm8T6mJe/YUamcgOlHbzAyBwAA\nVoaSCQAAQIl9TJGxrB+VWxIszFN7Y5leOj/kdxQAAJAmKJkAAAAkdUSiml2I68FtlExL3nF/pU71\nRjU2Oed3FAAAkAYomQAAALS49FuSHthCybTknTsrFXfSqxc4zQQAAO6NkgkAAEDS8Suj2lFdqnBx\nnt9RUkZbQ5mCBbmMzAEAgBWhZAIAAFkvHnc6fmVUD2wt9ztKSsnNCeih+zbppXMs/wYAAPdGyQQA\nALLexaGbGpua0wFKpp/yyI5KRUamdGV4wu8oAAAgxVEyAQCArHf8SmIfEyXTT3nH/ZWSpFfOD/uc\nBAAApDpKJgAAkPWOXxlVWXGetleW+B0l5WyrLFF1sEA/uUTJBAAA7o6SCQAAZL3jV0b1wJZymZnf\nUVKOmenwtgr95OKInHN+xwEAACmMkgkAAGS10YlZXRicYB/TXTy4fZMGYtOKjEz5HQUAAKQwSiYA\nAJDVTkYW9zEdpGS6owe3VUiSXmNkDgAA3AUlEwAAyGrHr4wqN2Da11Dmd5SUtaO6VBUl+TpyacTv\nKAAAIIVRMgEAgKx2/MqoWutCKsrP8TtKyjIzHWoqZ/k3AAC4K0omAACQteYW4uqMjLGPaQUOb9uk\nyMiUrkXZywQAAG6PkgkAAGStnv6YpuYW9AAl0z0t7WViZA4AANwJJRMAAMhax68sLv2mZLq35tqQ\nivNzdOLqqN9RAABAiqJkAgAAWev4lVHVhQtVGy7yO0rKywmY2hrK1BGJ+h0FAACkKEomAACQtU5c\nGWUf0yq0bylT97WYpucW/I4CAABSECUTAADISteiU7o2Ns2o3CrsbyzTfNzpdN+Y31EAAEAKomQC\nAABZ6eTVxbGvA1somVaqfUuZJDEyBwAAbouSCQAAZKWOyKjycwNqrg35HSVtVAcL1VBe9GZBBwAA\nsBwlEwAAyEonr0a1py6k/Fy+Dq1Ge2OZTvKEOQAAcBt8qwIAAFlnbiGuU31jam9kVG619m8p17Wx\naV2PTfsdBQAApBhKJgAAkHXODoxrZj7+5o4hrNz+xP9mnGYCAAC3omQCAABZ52RicfX+Rkqm1Wqp\nDSk3YHq9lyfMAQCAt6JkAgAAWafjalSbSvLVUF7kd5S0U5iXo52bgzp9LeZ3FAAAkGIomQAAQNbp\niIyqvbFMZuZ3lLS0pz6k031jcs75HQUAAKQQSiYAAJBVxqbmdGFwQu2Myq3Z3vqwRiZm1T/G8m8A\nAPCPKJkAAEBWeb13cR8TS7/XrrU+LEk61cdeJgAA8I8omQAAQFbpuLpYMu1roGRaq+aakAImdVEy\nAQCAZSiZAABAVumIRHV/danCRXl+R0lbRfk52lEd5CQTAAB4C0omAACQNZxzOhmJso8pCVrrQzxh\nDgAAvAUlEwAAyBqRkSmNTMxSMiXB3vqwBsdndCPG8m8AALCIkgkAAGSNk5FRSaJkSoI9LP8GAAC3\noGQCAABZoyMSVWFeQLtrgn5HSXsttSGZSaf7GJkDAACLKJkAAEDW6IhEtbc+rNwcvgKtV0lBrrZW\nFOvMACUTAABYxDcsAACQFWbn4+q6FmNULomaa0M6MzDudwwAAJAiKJkAAEBW6OmPaXY+rvbGcr+j\nZIzdNSFdHp7Q5Oy831EAAEAKoGQCAABZoSMSlSS1b+EkU7I01wblnHSW00wAAECUTAAAIEt0RKKq\nChaoLlzod5SM0VwbkiRG5gAAgCRKJgAAkCU6IlG1N5bJzPyOkjHqy4pUWpCrnn6WfwMAAI9LJjN7\nzMzOmtl5M/v0bd7/hJmdMrMOM3vZzFqWvfd7ifvOmtmjXuYEAACZbXRiVpeGJrSfUbmkCgRMu2uC\nOtPPSSYAAOBhyWRmOZK+KOlxSS2SPry8REr4qnNur3OuXdLnJH0+cW+LpKcktUp6TNK/T/w8AACA\nVevoTexj4slySbe7NqiegZicc35HAQAAPvPyJNNhSeedcxedc7OSnpH05PIPOOeWn60ukbT07eRJ\nSc8452acc5cknU/8PAAAgFXruBqVmbSvgZIp2XbXhDQ+Pa++6JTfUQAAgM+8LJnqJUWWve5NXHsL\nM/ukmV3Q4kmmf7maewEAAFaiIxLVzuqgSgty/Y6Scd5c/s3IHAAAWc/3xd/OuS865+6T9LuS/nA1\n95rZx83smJkdGxwc9CYgAABIa845dfZGGZXzyK6aoCSx/BsAAHhaMvVJalz2uiFx7U6ekfSh1dzr\nnPuyc+6gc+5gVVXVOuMCAIBMdHl4UtHJObWz9NsTpQW52rqpWGcGOMkEAEC287JkOipph5ltM7N8\nLS7yfnb5B8xsx7KXH5B0LvH3ZyU9ZWYFZrZN0g5JRzzMCgAAMlRHZFQSS7+9tLsmyEkmAAAgzxYT\nOOfmzexpSc9LypH0Fedcl5l9VtIx59yzkp42s/dImpM0KuljiXu7zOxrkrolzUv6pHNuwausAAAg\nc3Vcjao4P0c7Nwf9jpKxdteE9EL3dU3NLqgonwcCAwCQrTzdfumce07Sc7dc+8yyv//WXe79Y0l/\n7F06AACQDToiUe2tDysnYH5HyVjNtSE5J71xfVxtnBgDACBr+b74GwAAwCvTcwvq7o+xj8ljzbUs\n/wYAAJRMAAAgg3Vdi2luwWk/p2s81VherJL8HJZ/AwCQ5SiZAABAxuqMRCVJ7Y3lPifJbIGAaVdN\nUN2cZAIAIKtRMgEAgIzV2RtVTahQNeFCv6NkvN21IZ3pj8k553cUAADgE0omAACQsTojUbU1hv2O\nkRWaa0OKTc+rf2za7ygAAMAnlEwAACAjRSdndXl4kqedbZDmGpZ/AwCQ7SiZAABARursHZMktTdQ\nMm2EXZRMAABkPUomAACQkTojUZlJexoYl9sIwcI8NVYUqYcnzAEAkLUomQAAQEbqjER1X1WpQoV5\nfkfJGs01IU4yAQCQxSiZAABAxnHOqSMSVTv7mDbU7tqQLg9NaGp2we8oAADAB5RMAAAg4/SOTml4\nYpal3xuspTaouJPeuM7IHAAA2YiSCQAAZJzO3qgkln5vtObakCSWfwMAkK0omQAAQMbpjESVnxt4\n84ln2BiN5cUqyc+hZAIAIEtRMgEAgIzTGRlTa11I+bl81dlIgYBpV02QJ8wBAJCl+OYFAAAyyvxC\nXKf6xtTGqJwvmmsXnzDnnPM7CgAA2GCUTAAAIKOcu3FTU3MLPFnOJ821IY1Pz6svOuV3FAAAsMEo\nmQAAQEbpjCwu/ebJcv5YWv59pp+ROQAAsg0lEwAAyCidvVGFCnPVtKnY7yhZaWnZOsu/AQDIPpRM\nAAAgo3RExtTWWCYz8ztKViotyNXWTcXqGaBkAgAg21AyAQCAjDE5O6+zAzHtZ1TOV801IfUwLgcA\nQNahZAIAABnjdF9Mccc+Jr/trg3q8vCEJmfn/Y4CAAA2ECUTAADIGEtLv/c1UDL5qbk2JOekswOc\nZgIAIJtQMgEAgIzR0RtVfVmRqoIFfkfJai2JJ8wxMgcAQHahZAIAABmjMxJVO6NyvmsoL1JpQa7O\nsPwbAICsQskEAAAywtDNGfWOTqmtMex3lKxnZtpdE1RPPyUTAADZhJIJAABkhNd7F/cxtbGPKSU0\n14Z0pn9czjm/owAAgA1CyQQAADJCR2RMAZP21HOSKRU014Y0PjOv3tEpv6MAAIANQskEAAAyQmck\nqp2bgyopyPU7CiQ11wYliZE5AACyCCUTAABIe845dfZGGZVLIbtqgjLjCXMAAGQTSiYAAJD2rgxP\nKjo5p/YtlEypojg/V9s2lai7f8zvKAAAYINQMgEAgLTXydLvlNRcF1I343IAAGQNSiYAAJD2OiJR\nFeYFtHNzqd9RsExrXUiRkSmNTc35HQUAAGwASiYAAJD2OiNR7a0PKzeHrzappLVu8Ul/3dc4zQQA\nQDbgmxgAAEhrcwtxnb4WY1QuBbXUhiRJXdfYywQAQDagZAIAAGnt7MC4ZufjamukZEo1VcECVQcL\n2MsEAECWoGQCAABprSOyuPS7nZIpJbXWhRiXAwAgS1AyAQCAtNYZiaqiJF8N5UV+R8FttNSFdO7G\nTU3PLfgdBQAAeIySCQAApLXO3qjaGsIyM7+j4DZa68JaiDudu37T7ygAAMBjlEwAACBt3ZyZ17kb\nN9nHlMJa61j+DQBAtqBkAgAAaev13qicYx9TKmssL1awIFdd7GUCACDjUTIBAIC01RlZPB3T1kDJ\nlKoCAVNzbYiTTAAAZAFKJgAAkLY6I1Ft3VSs8pJ8v6PgLlrqQjozMK6FuPM7CgAA8BAlEwAASFuL\nS785xZTqWutCmpxd0OXhCb+jAAAAD1EyAQCAtHQ9Nq3+sWmWfqeBljeXf7OXCQCATEbJBAAA0lJn\nJCpJam8M+5wE97KjOqi8HFM3JRMAABmNkgkAAKSlzt6ocgKm1jpKplSXnxvQzs1Bln8DAJDhKJkA\nAEBa6oyMaXdNUIV5OX5HwQq01oXUfS0m51j+DQBApqJkAgAAaSced4tLv9nHlDZaakManpjV9diM\n31EAAIBHKJkAAEDauTQ8ofHpebXzZLm00Vq/ONbY3c/IHAAAmYqSCQAApJ2lpd+cZEofzbWJJ8z1\nsfwbAIBMRckEAADSTmckquL8HN1fXep3FKxQaUGumjYVq4snzAEAkLEomQAAQNrp6B3T3vqwcgLm\ndxSsQmtdWN39lEwAAGQqSiYAAJBWZufj6rkWUzujcmmnpS6kqyOTik3P+R0FAAB4wNOSycweM7Oz\nZnbezD59m/d/28y6zex1M/uumW1d9t6CmXUk/jzrZU4AAJA+zgzENLsQZx9TGmqpW9zL1M3IHAAA\nGcmzksnMciR9UdLjklokfdjMWm752ElJB51z+yT9naTPLXtvyjnXnvjzhFc5AQBAemHpd/pqTZRM\n7GUCACAzeXmS6bCk8865i865WUnPSHpy+Qecc993zk0mXr4mqcHDPAAAIAN0RMZUWVqgunCh31Gw\nStXBQlUFCzjJBABAhvKyZKqXFFn2ujdx7U5+XdK3l70uNLNjZvaamX3Ii4AAACD9dPZG1dYQlhlL\nv9NRa11IXdfG/I4BAAA8kBKLv83so5IOSvq3yy5vdc4dlPQRSV8ws/tuc9/HE0XUscHBwQ1KCwAA\n/BKbntOFwZuMyqWxltqQzt+4qZn5Bb+jAACAJPOyZOqT1LjsdUPi2luY2Xsk/YGkJ5xzM0vXnXN9\niX9elPQDSftvvdc592Xn3EHn3MGqqqrkpgcAACnndO+YnGMfUzprrQtrPu507vpNv6MAAIAk87Jk\nOipph5kzM5IDAAAgAElEQVRtM7N8SU9JestT4sxsv6QvabFgurHsermZFST+XinpYUndHmYFAABp\noKM3sfS7IexzEqzVPy7/ZmQOAIBMk+vVD3bOzZvZ05Kel5Qj6SvOuS4z+6ykY865Z7U4Hlcq6W8T\nexWuJp4k1yzpS2YW12IR9ifOOUomAACyXGckqqZNxSorzvc7CtZoS0WxSgtyecIcAAAZyLOSSZKc\nc89Jeu6Wa59Z9vf33OG+VyXt9TIbAABIP52RMT24vcLvGFiHQMDUXBukZAIAIAOlxOJvAACAe7ke\nm9ZAbFptDexjSnetdWH19McUjzu/owAAgCSiZAIAAGmhM5LYx8TS77TXUhvS5OyCLg9P+B0FAAAk\nESUTAABIC529UeUG7M3F0UhfLW8u/2ZkDgCATELJBAAA0kJnZEy7a4MqzMvxOwrWaefmoPJyTN39\nlEwAAGQSSiYAAJDy4nGnzt4o+5gyRH5uQDuqWf4NAECmoWQCAAAp79LwhMan59nHlEFa6kLqvjYm\n51j+DQBApqBkAgAAKW9p6Xc7JVPGaK0LaejmrG6Mz/gdBQAAJAklEwAASHmdkaiK83N0X1Wp31GQ\nJK11YUlSNyNzAABkDEomAACQ8k71jWlPXVg5AfM7CpKkuTYoSeq6NuZzEgAAkCyUTAAAIKUtxJ26\n+2NqrQ/5HQVJFCzM09ZNxSz/BgAgg1AyAQCAlHZh8Kam5+LaWx/2OwqSrLUupO5+SiYAADIFJRMA\nAEhpp/sWx6n2UDJlnNa6sK4MTyo2Ped3FAAAkASUTAAAIKWd6htTYV6Apd8ZqKV2cQSyh5E5AAAy\nAiUTAABIaV19MbXUhlj6nYFa6xZLJvYyAQCQGSiZAABAyorHnbqujbGPKUNVhwpVWVrAXiYAADIE\nJRMAAEhZl4YnNDG7oFZKpozVUhfiJBMAABmCkgkAAKSspaXfnGTKXK11IZ27Pq6Z+QW/owAAgHWi\nZAIAACnrdN+Y8nMDur+apd+ZqrUupPm407nrN/2OAgAA1omSCQAApKxTfWNqrgkqL4evLJlq6Qlz\n3YzMAQCQ9vjGBgAAUlI87tTVF9MeRuUyWtOmEpXk56jr2pjfUQAAwDpRMgEAgJR0dWRS4zPzlEwZ\nLhAwNdey/BsAgExAyQQAAFLS6Wss/c4WrXUh9fTHFI87v6MAAIB1oGQCAAAp6VTfmPJyTDs2s/Q7\n07XUhTQxu6ArI5N+RwEAAOtAyQQAAFJSV19Mu2qCKsjN8TsKPNZat3hajb1MAACkN0omAACQcpxz\nOtU3pj11jMplgx2bS5UbMJ4wBwBAmqNkAgAAKad3dEpjU3Ms/c4SBbk5ur+6VKcpmQAASGuUTAAA\nIOUsjU1RMmWPvfVhdfWNyTmWfwMAkK4omQAAQMo51TemnIBpd03Q7yjYIHsbwhqemFX/2LTfUQAA\nwBpRMgEAgJTTdS2mHdWlKsxj6Xe2WDq19novy78BAEhXlEwAACDl9PTH1Fwb8jsGNlBLbUg5AdPp\nPkomAADSFSUTAABIKSMTs7oem1FzLaNy2aQwL0c7qkv1OiUTAABpi5IJAACklJ7+xSeMcZIp++xr\nCOs0y78BAEhblEwAACClUDJlr731YY1MzKovOuV3FAAAsAaUTAAAIKV098dUFSxQZWmB31GwwZaW\nf7OXCQCA9ETJBAAAUkpP/zinmLJUc21IuQHTKUomAADSEiUTAABIGbPzcZ2/Mc7S7yxVmJejHZuD\ner2XkgkAgHREyQQAAFLGhcGbmltwauEkU9baV8/ybwAA0hUlEwAASBlnBlj6ne32NIQ1Ojmn3lGW\nfwMAkG4omQAAQMro6R9Xfk5A2ytL/I4Cn+xj+TcAAGmLkgkAAKSMnv6YdmwuVW4OX1Gy1a6aIMu/\nAQBIU3yDAwAAKaOnP8aoXJYrzMvRzs1BSiYAANIQJRMAAEgJN8anNXRzlpIJamssU2ckqnic5d8A\nAKQTSiYAAJASevrHJUnNtUGfk8Bv+7eUKTY9r4tDE35HAQAAq7CiksnM/quZfcDMKKUAAIAnevoX\nnyzXwkmmrHdgS5kk6cTVUZ+TAACA1VhpafTvJX1E0jkz+xMz2+VhJgAAkIV6+mOqDReqrDjf7yjw\n2fbKUoUKc3XyatTvKAAAYBVWVDI55150zv33kg5IuizpRTN71cz+mZnleRkQAABkB5Z+Y0kgYGrf\nUq6TnGQCACCtrHj8zcw2Sfqnkn5D0klJ/7cWS6fveJIMAABkjem5BV0YnGAfE960v7FMb1wf182Z\neb+jAACAFVrpTqZvSHpJUrGk/84594Rz7m+cc/+jpFIvAwIAgMx3/sZNLcQdJ5nwpv1byhR30uu9\njMwBAJAuVnqS6U+dcy3Ouf/NOdcvSWZWIEnOuYOepQMAAFlhaek3JROW7G8slyT2MgEAkEZWWjL9\n69tc+3EygwAAgOzV0z+uwryAmjaV+B0FKSJcnKf7qkrYywQAQBrJvdubZlYjqV5SkZntl2SJt0Ja\nHJ0DAABYt57+mHbVhJQTsHt/GFlj/5Zyff/MDTnnZMb/NwAASHV3LZkkParFZd8Nkj6/7Pq4pN/3\nKBMAAMgizjn1DMT0+J4av6MgxezfUqa/O96ryMiUtmziv28CAJDq7loyOef+XNKfm9kvOOe+vkGZ\nAABAFhmITSs6OafdNexjwlu9uZcpMkrJBABAGrjXuNxHnXN/JanJzH771vedc5+/zW0AAAArxtJv\n3MnOzaUqzs/RyatRPdle73ccAABwD/da/L20fbNUUvA2f+7KzB4zs7Nmdt7MPn2b93/bzLrN7HUz\n+66ZbV323sfM7Fziz8dW/G8EAADSSk//uCRpd+09v1ogy+TmBNTWUKYTLP8GACAt3Gtc7kuJf/6v\nq/3BZpYj6YuS3iupV9JRM3vWOde97GMnJR10zk2a2T+X9DlJv2JmFZL+F0kHJTlJxxP38g0DAIAM\n090fU0N5kUKFeX5HQQp6YGu5/sMPL2hiZl4lBfdaJwoAAPx0r5NMkiQz+5yZhcwsL3HiaNDMPnqP\n2w5LOu+cu+icm5X0jKQnl3/AOfd959xk4uVrWlwwLi0uHP+Oc24kUSx9R9JjK/2XAgAA6eNMf4xR\nOdzRoW0VWog7nbwa9TsKAAC4hxWVTJLe55yLSfqgpMuS7pf0O/e4p15SZNnr3sS1O/l1Sd9ezb1m\n9nEzO2ZmxwYHB+8RBwAApJrpuQVdGpqgZMIdHdhSpoBJRy6P+B0FAADcw0pLpqWzyR+Q9LfOubFk\nhkicijoo6d+u5j7n3JedcwedcwerqqqSGQkAAGyAswPjijupuYZ9TLi9YGGeWupCOnqJkgkAgFS3\n0pLpv5nZGUkPSPqumVVJmr7HPX2SGpe9bkhcewsze4+kP5D0hHNuZjX3AgCA9HZmgCfL4d4ONVXo\nxNVRzc7H/Y4CAADuYkUlk3Pu05LersUl3XOSJnTLfqXbOCpph5ltM7N8SU9Jenb5B8xsv6QvabFg\nurHsreclvc/Mys2sXNL7EtcAAEAG6ekfV3F+jrZUFPsdBSnscFOFZubjOtWX1MP0AAAgyVbziI7d\nkprMbPk9f3GnDzvn5s3saS2WQzmSvuKc6zKzz0o65px7VovjcaWS/tbMJOmqc+4J59yImf0rLRZV\nkvRZ5xxnpAEAyDA9/THtqgkqEDC/oyCFHWyqkCQdvTyiB7aW+5wGAADcyYpKJjP7S0n3SeqQtJC4\n7HSXkkmSnHPPSXrulmufWfb399zl3q9I+spK8gEAgPTjnFNPf0wfbKvzOwpSXFWwQNurSnT00og+\n8TP3+R0HAADcwUpPMh2U1OKcc16GAQAA2ePa2LRi0/PsY8KKHG6q0HOn+hWPO06+AQCQola6+Pu0\npBovgwAAgOxypj+x9Jsny2EFDjVVKDY9r7PXx/2OAgAA7mClJ5kqJXWb2RFJS0+Ak3PuCU9SAQCA\njNeTKJl2c5IJK3B42z/uZeL0GwAAqWmlJdMfeRkCAABkn57+cW2pKFZpwWqeQ4Js1VBepJpQoY5c\nGtGvva3J7zgAAOA2VvStzjn3QzPbKmmHc+5FMyvW4hPjAAAA1qRnIKbdjMphhcxMh7ZV6MilYTnn\nlHgyMQAASCEr2slkZv+DpL+T9KXEpXpJf+9VKAAAkNmmZhd0eWiCsSesyuGmcl2PzSgyMuV3FAAA\ncBsrXfz9SUkPS4pJknPunKRqr0IBAIDMdvb6uOJOlExYlUOJvUxHLo/4nAQAANzOSkumGefc7NIL\nM8uV5LyJBAAAMt2bT5arZVwOK7ezOqhwUZ6OXBr2OwoAALiNlZZMPzSz35dUZGbvlfS3kr7pXSwA\nAJDJevpjKsnPUWN5sd9RkEYCAdOhpnIdvTzqdxQAAHAbKy2ZPi1pUNIpSb8p6TlJf+hVKAAAkNl6\nBsa1uzakQIDlzVidQ00VujQ0oRvj035HAQAAt1hRyeSci2tx0fe/cM79onPuT51zjMsBAIBVc86p\np58ny2FtlvYyHeM0EwAAKeeuJZMt+iMzG5J0VtJZMxs0s89sTDwAAJBp+qJTGp+eZ+k31mRPXViF\neQEducTybwAAUs29TjJ9SotPlTvknKtwzlVIelDSw2b2Kc/TAQCAjHOmf1wST5bD2uTnBrS/sVxH\necIcAAAp514l069K+rBz7tLSBefcRUkflfRrXgYDAACZqSfxZLldjMthjQ5vq1B3f0yx6Tm/owAA\ngGXuVTLlOeeGbr3onBuUlOdNJAAAkMl6BmLauqlYpQW5fkdBmjq8rULOScevsJcJAIBUcq+SaXaN\n7wEAANxW97WYmmsYlcPa7d9SptyA6Sh7mQAASCn3+k+IbWYWu811k1ToQR4AAJDBYtNzujw8qV86\n2Oh3FKSx4vxctdaH2csEAECKuetJJudcjnMudJs/Qecc43IAAGBVuvoW/9tVax0nmbA+h5vK1RkZ\n0/Tcgt9RAABAwr3G5QAAAJLmdN+YJGlvfdjnJEh3h7dt0uxCXK/3jvkdBQAAJFAyAQCADXP62pjq\nwoXaVFrgdxSkuYNbyyVJRy4N+5wEAAAsoWQCAAAb5lTfmFo5xYQkKC/J187NpTpymSfMAQCQKiiZ\nAADAhrg5M69LQxOMyiFpDjVV6MSVUS3End9RAACAKJkAAMAG6b4Wk3PsY0LyHN5WoZsz8+rpv93D\nkAEAwEajZAIAABviVGLpd2s9T5ZDchxqqpAkHbk04nMSAAAgUTIBAIANcrpvTJtDBaoOFvodBRmi\nrqxIDeVFOnqZkgkAgFRAyQQAADbE6b4xRuWQdIebKnTk0oicYy8TAAB+o2QCAACem5yd14XBm2qt\no2RCch1sqtDwxKyuDE/6HQUAgKxHyQQAADzXfS2mOEu/4YEDW8skSSeujvqcBAAAUDIBAADPnU4s\n/d5DyYQk21EdVGlBro5foWQCAMBvlEwAAMBzp/piqiwt0OZQgd9RkGFyAqb9W8p04mrU7ygAAGQ9\nSiYAAOC5031j2lMfkpn5HQUZaP+Wcp0diOnmzLzfUQAAyGqUTAAAwFM3Z+b1xo1xtTeW+R0FGeqB\nreWKO6kzwmkmAAD8RMkEAAA89XokKucWT5sAXlgqME+wlwkAAF9RMgEAAE+dTJwuaW/gJBO8ES7K\n087NpTrOE+YAAPAVJRMAAPDUyaujuq+qROHiPL+jIIMd2FKuk1ejised31EAAMhalEwAAMAzzjmd\nvBpVeyOjcvDWga3lGpua08Whm35HAQAga1EyAQAAz0RGpjQ8Mav9WxiVg7cOJHZ+nbjC8m8AAPxC\nyQQAADxzMrK4I4eSCV7bXlmicFGeTrCXCQAA31AyAQAAz5y8GlVRXo52bQ76HQUZLhAwHdhSpuM8\nYQ4AAN9QMgEAAM+cvDqqfQ1h5ebwlQPeO7ClXOdu3NTY1JzfUQAAyEp84wMAAJ6YnJ1X17WYDmxl\n6Tc2RntiLPNU75jPSQAAyE6UTAAAwBMdV6OajzsdbqrwOwqyxL6GxZKps5fl3wAA+IGSCQAAeOLI\n5RGZiZNM2DDhojxtrypRR4SSCQAAP1AyAQAATxy9PKLdNSGFi/L8joIs0t5Qpo5IVM45v6MAAJB1\nKJkAAEDSzS3EdeJKVIebOMWEjdXWWKbB8Rn1j037HQUAgKxDyQQAAJKu61pMU3MLOrSNfUzYWG2N\nib1MjMwBALDhKJkAAEDSHb00Ikks/caGa64NKj8noA6WfwMAsOEomQAAQNIduTyirZuKVR0q9DsK\nskxBbo6a60LquErJBADARqNkAgAASRWPOx27PKJDnGKCT9obwjrVN6aFOMu/AQDYSJRMAAAgqbr7\nYxqdnNPb79vkdxRkqbbGMk3OLuj8jZt+RwEAIKtQMgEAgKR69cKQJOnh+yt9ToJsxfJvAAD8QckE\nAACS6pXzw7qvqkSb2ccEn2zbVKJQYa5OUjIBALChKJkAAEDSzM7HdeTSCKeY4KtAwNTWWMZJJgAA\nNpinJZOZPWZmZ83svJl9+jbvv9PMTpjZvJn94i3vLZhZR+LPs17mBAAAydERiWpqbkFvv4+SCf5q\nayjT2evjmppd8DsKAABZw7OSycxyJH1R0uOSWiR92MxabvnYVUn/VNJXb/Mjppxz7Yk/T3iVEwAA\nJM8r54cUMOlt21n6DX+1NZZpIe7UdW3M7ygAAGQNL08yHZZ03jl30Tk3K+kZSU8u/4Bz7rJz7nVJ\ncQ9zAACADfLqhSHtqQ8rXJzndxRkubbGsKTF03UAAGBjeFky1UuKLHvdm7i2UoVmdszMXjOzD93u\nA2b28cRnjg0ODq4nKwAAWKeJmXmdvBplVA4poTpYqPqyIkomAAA2UCov/t7qnDso6SOSvmBm9936\nAefcl51zB51zB6uqqjY+IQAAeNPRyyOajzs9fD+jckgNbY1hdfZSMgEAsFG8LJn6JDUue92QuLYi\nzrm+xD8vSvqBpP3JDAcAAJLr1QvDys8J6ODWCr+jAJIWl39HRqY0fHPG7ygAAGQFL0umo5J2mNk2\nM8uX9JSkFT0lzszKzawg8fdKSQ9L6vYsKQAAWLdXzg/pwNYyFeXn+B0FkLS4/FuSXu9l+TcAABvB\ns5LJOTcv6WlJz0vqkfQ151yXmX3WzJ6QJDM7ZGa9kn5J0pfMrCtxe7OkY2bWKen7kv7EOUfJBABA\nihqdmFV3f0wPs48JKWRvfVgBY/k3AAAbJdfLH+6ce07Sc7dc+8yyvx/V4hjdrfe9Kmmvl9kAAEDy\n/PjisJyT3n4/JRNSR0lBrnZUB9nLBADABknlxd8AACBNvHJ+SKUFuWprCPsdBXiLtsawOiNROef8\njgIAQMajZAIAAOv26oVhPbitQrk5fLVAamlrLNPo5JwiI1N+RwEAIOPxTRAAAKzLteiULg1NMCqH\nlNTWsLj8u4OROQAAPEfJBAAA1uWV80OSpIfv3+RzEuCn7aoJqiA3oE6WfwMA4DlKJgAAsC6vXhhW\nZWm+dm0O+h0F+Cl5OQHtqQ9TMgEAsAEomQAAwJo55/TqhSG97b5KmZnfcYDbamso0+lrY5pbiPsd\nBQCAjEbJBAAA1uzi0ISux2b09vsYlUPqamsMa3ourjeuj/sdBQCAjEbJBAAA1uzHF4YlSW/bTsmE\n1NXeuLj8uzMy5nMSAAAyGyUTAABYsx9fHFZtuFBbNxX7HQW4oy0VxSorzmMvEwAAHqNkAgAAa+Kc\n008uDuuh7ZvYx4SUZmZqayhTZy8lEwAAXqJkAgAAa3Luxk0N3ZxlVA5poa2xTG9cH9fEzLzfUQAA\nyFiUTAAAYE3e3MfE0m+kgfbGsOJOOt3HXiYAALxCyQQAANbktYvDqi8rUmMF+5iQ+vY1JJZ/MzIH\nAIBnKJkAAMCqxeNOr10c5hQT0kZlaYEayot4whwAAB6iZAIAAKt29vq4Rifn2MeEtNLWWKYOnjAH\nAIBnKJkAAMCqLe1jeoiTTEgj7Q1l6otOaXB8xu8oAABkJEomAACwaj++OKwtFcWqLyvyOwqwYm2N\ni3uZXmcvEwAAnqBk+v/bu/P4quo7/+Pvz703CwkhZAOyQEAW2WWJILi14q4Vi9alq21nOrZ1Op3+\n+ptpp4sdO7/+ukxnpp12qna0M+1oa1uXUhWtS0urArIKRMIWtoQskIQQyHrv/c4f92ojBkhMbs5d\nXs/HI4+ce8+5lzd4POfmnfP9HgAAMCChsNO66iaGyiHhzC4dJZ9Jr9UwLxMAALFAyQQAAAZkR91x\nHe8MMuk3Ek5WekDTxuboNeZlAgAgJiiZAADAgLwxHxMlExLRvPGj9VrNMTnnvI4CAEDSoWQCAAAD\nsra6SecUZmvsqEyvowADdt740TrW3qMDTe1eRwEAIOlQMgEAgH4LhsJ6dV8zd5VDwpo/ITL598YD\nLR4nAQAg+VAyAQCAfqs8fFxtXUEm/UbCmjYmRzkZAW08SMkEAMBQo2QCAAD9tqY6Mh/T4nPyPU4C\nvDM+n2l+eZ427qdkAgBgqFEyAQCAfluzt0lTxozUmBzmY0LiqijP067GNrV29HgdBQCApELJBAAA\n+qUnFNb6/c0MlUPCqyjPk3PSZobMAQAwpCiZAABAv2ytaVV7d0hLmPQbCe688aPl95k2Mfk3AABD\nipIJAAD0y9rofEwXcCUTElx2RkAzinO0gZIJAIAhRckEAAD6Zc3eJk0fl6P87HSvowCDtnBCnrYc\nOqZgKOx1FAAAkgYlEwAAOKvuYFgbDjRzFROSxsKJ+WrvDqmqvs3rKAAAJA1KJgAAcFav1RxTZ0+Y\nkglJY2F5niRpI0PmAAAYMpRMAADgrNbsbZKZdME5+V5HAYZE6egRKs7NZF4mAACGECUTAAA4qzV7\nmzRj3CiNzmI+JiSPBeV53GEOAIAhRMkEAADOqLMnpI0HW7RkMkPlkFwqyvNUe6xDda0dXkcBACAp\nUDIBAIAz2nzwmLqDYS1hPiYkmfMnRoZ/vrqv2eMkAAAkB0omAABwRmuqm+Qz6fxJzMeE5DKjeJRy\nMgNaW93kdRQAAJICJRMAADijtXubNKskV7kj0ryOAgwpv8+0eFK+1lZzJRMAAEOBkgkAAJxWR3dI\nWw4dYz4mJK0LzinQvqMnVd/a6XUUAAASHiUTAAA4rQ0HmtUdClMyIWldEJ1rbN0+hswBADBYlEwA\nAOC0XtnbpIDPtGgi8zEhOTEvEwAAQ4eSCQAAnNYre45q3vjRys4IeB0FiAnmZQIAYOhQMgEAgD61\ndvRoW22rlk4p9DoKEFPMywQAwNCgZAIAAH1aV92ksJMuZD4mJLk35mV6Ze9Rj5MAAJDYKJkAAECf\nXtnbpMw0n+ZNGO11FCCmZhaPUkF2ul7aTckEAMBgUDIBAIA+vbznqM6fmK+MgN/rKEBM+XymC6cU\n6k97jso553UcAAASFiUTAAB4m8bjndrdeEIXMh8TUsRFUwt1pK1LOxvavI4CAEDComQCAABvsyZ6\nO/elzMeEFHHx1Eih+qddDJkDAOCdomQCAABv8/KeoxqVGdCsklyvowDDojh3hKaMGak/7aFkAgDg\nnaJkAgAAb+Gc08t7mrRkcoH8PvM6DjBsLp5aqHXVTersCXkdBQCAhETJBAAA3uJgc7tqj3Vo6WTm\nY0JquXhqobqCYa3f3+x1FAAAEhIlEwAAeIs/7joiSbpkWpHHSYDhteScQmUEfHphR6PXUQAASEiU\nTAAA4C1W7zqiCflZmliQ5XUUYFiNSPfrwimFeqGqQc45r+MAAJBwKJkAAMCbuoIhvbK3SZdOK5IZ\n8zEh9Vw2fYwONXdoT+MJr6MAAJBwYloymdnVZrbTzPaY2Rf6WH+JmW0ys6CZ3XzKuo+Y2e7o10di\nmRMAAERs3N+i9u4QQ+WQspbNGCNJep4hcwAADFjMSiYz80v6oaRrJM2UdLuZzTxls4OS7pD08Cmv\nzZd0t6TFkhZJutvM8mKVFQAARKzedURpftOSyQVeRwE8UZw7QrNKRumFHQ1eRwEAIOHE8kqmRZL2\nOOeqnXPdkn4haXnvDZxz+51zWyWFT3ntVZKec841O+daJD0n6eoYZgUAAIqUTBXl+RqZEfA6CuCZ\nZdPHaNPBFjWf7PY6CgAACSWWJVOppEO9HtdEn4v1awEAwDvQcLxTVfVtuvRchsohtS2bMVZhJ/1h\nJ0PmAAAYiISe+NvMPmFmG8xsw5EjR7yOAwBAQlu9K3IuvZT5mJDi5pTmqignQy8wLxMAAAMSy5Kp\nVtL4Xo/Los8N2Wudc/c75yqccxVFRXwgBgBgMFbvOqIxORmaPi7H6yiAp3w+07LpY7R61xF1B0+d\n1QEAAJxOLEum9ZKmmtkkM0uXdJuklf187bOSrjSzvOiE31dGnwMAADEQDIX10u6junRakczM6ziA\n5y6bPkYnuoJat6/J6ygAACSMmJVMzrmgpLsUKYd2SPqlc67SzO4xsxskyczON7MaSe+TdJ+ZVUZf\n2yzp64oUVesl3RN9DgAAxMBrNcfU2tGjSxgqB0iSLp5apBFpfq3aXu91FAAAEkZMbx3jnHta0tOn\nPPfVXsvrFRkK19drH5T0YCzzAQCAiOd3NCrgM0omIGpEul/LZozRM9vrdc8NsxTwJ/RUpgAADAvO\nlgAAQM+/3qBFk/KVOyLN6yhA3LhuTrGaT3Zr3T4uqAcAoD8omQAASHEHm9q1u/GEls0Y63UUIK68\n69wxykr368mtdV5HAQAgIVAyAQCQ4p7f0SBJunzGGI+TAPElMmRurJ6trFcwxF3mAAA4G0omAABS\n3AtVDZoyZqTKC7K9jgLEnevmjFPzyW6trWbIHAAAZ0PJBABACjve2aN11c1axlVMQJ/eGDL31LbD\nXkcBACDuUTIBAJDCVu88omDY6QrmYwL6lJkWGTL3zHaGzAEAcDaUTAAApLAXdjQoPztd8yfkeR0F\niFvXzSlWS3uPXtnb5HUUAADiGiUTAAApKhgK6/c7j+hd5xbJ7zOv4wBx613nFiknM6AnNtd6HQUA\ngE2PFB4AACAASURBVLhGyQQAQIracKBFrR09upyhcsAZZab5df3cYq3aXq8TXUGv4wAAELcomQAA\nSFHPbK9XesCnS6cVeR0FiHs3LShTR09Iq7bVeR0FAIC4RckEAEAKcs7p2cp6XTK1SNkZAa/jAHFv\nYXmeyguy9NgmhswBAHA6lEwAAKSgrTWtqmvt1DWzx3kdBUgIZqYV88u0prpJNS3tXscBACAuUTIB\nAJCCVm2vV8BnWjZjjNdRgISxYkGpJOlxrmYCAKBPlEwAAKQY55ye2V6nJZMLNDor3es4QMIYn5+l\nxZPy9djmWjnnvI4DAEDcoWQCACDF7Go4of1N7bqaoXLAgN20sEz7jp7UpoMtXkcBACDuUDIBAJBi\nVm2vk5l0xcyxXkcBEs61c4qVle7XI+sPeR0FAIC4Q8kEAECKeWZ7vSrK8zQmJ9PrKEDCGZkR0A3n\nlei3r9XpeGeP13EAAIgrlEwAAKSQ/UdPqqq+TVfPLvY6CpCw3r94gjp6QnpiMxOAAwDQGyUTAAAp\n5NnKeknSVbMYKge8U3NKczWrZJQeXneQCcABAOiFkgkAgBSyanu95pblqiwvy+soQMIyM71/8QRV\n1bdp86FjXscBACBuUDIBAJAi6lo7tOXQMV01i7vKAYO1fF6pstP9enjdQa+jAAAQNyiZAABIEau2\nRYbKXT2bkgkYrJEZAd0wr1RPbj2s1g4mAAcAQKJkAgAgZTy59bBmFo/S5KKRXkcBksIHFk9QZ0+Y\nCcABAIiiZAIAIAXUtLRr08Fjuv487ioHDJXZpbmaW5bLBOAAAERRMgEAkAKe2lonSbp+TonHSYDk\ncvuiCdrZ0KZNB1u8jgIAgOcomQAASAFPbq3TeWW5mlDAXeWAoXTDeSUamRHQQ0wADgAAJRMAAMlu\n/9GT2lbbqvecx1VMwFDLzgho+bwSPbW1Tq3tTAAOAEhtlEwAACS5J7celiRdO4f5mIBYeP/iCeoK\nhvXY5hqvowAA4ClKJgAAktyTW+tUUZ6nktEjvI4CJKVZJZEJwB9Zf4gJwAEAKY2SCQCAJLa7oU1V\n9W0MlQNi7JaK8aqqb9O22lavowAA4BlKJgAAkthvt9bJZ9I1c8Z5HQVIajfMK1Fmmk+PrD/kdRQA\nADxDyQQAQJJyzunJrYe1eFKBxuRkeh0HSGqjMtN07exirdxyWB3dIa/jAADgCUomAACS1I66NlUf\nOclQOWCYvK9ivNq6glq1vc7rKAAAeIKSCQCAJPWb12oV8Jmuns1QOWA4XHBOvsoLshgyBwBIWZRM\nAAAkoXDYaeWWw7p0WpHys9O9jgOkBDPTLRXjtW5fs/YfPel1HAAAhh0lEwAASWjdvmbVtXZq+fxS\nr6MAKeWmBWXymfSrjVzNBABIPZRMAAAkoSc21yo73a8rZoz1OgqQUsblZuqSaUV6fFOtwmHndRwA\nAIYVJRMAAEmmsyekp7fX6arZ4zQi3e91HCDlrFhQpsOtnVq7r8nrKAAADCtKJgAAkswfdjaqrTOo\n9zJUDvDElTPHKicjoMc21XodBQCAYUXJBABAknl8c62KcjK0dHKh11GAlJSZ5te1c4q1alud2ruD\nXscBAGDYUDIBAJBEWtt79PuqI7rhvBL5feZ1HCBlrVhQqpPdIf2ussHrKAAADBtKJgAAksjT2+vU\nHQrrxnkMlQO8dP7EfJXljdCjm2q8jgIAwLChZAIAIIk8sblWk4uyNbt0lNdRgJTm85lWzC/Vy3uO\nqr610+s4AAAMC0omAACSRO2xDq3b16wb55XKjKFygNdWLChT2ElPbGECcABAaqBkAgAgSazccliS\ntJyhckBcmFiYrYXleXp0Y42cc17HAQAg5iiZAABIEk9srtXC8jxNKMjyOgqAqBULSrW78YQqDx/3\nOgoAADFHyQQAQBLYUXdcOxvadOO8Eq+jAOjl+jklSvf7mAAcAJASKJkAAEgCj22qUcBnum4uJRMQ\nT3Kz0nT5zDFaueWwekJhr+MAABBTlEwAACS4nlBYj2+u1eUzxio/O93rOABOsWJ+mZpOduuPu454\nHQUAgJiiZAIAIMH9vqpRR090630VZV5HAdCHS88tUn52uh7bxF3mAADJjZIJAIAE98sNNSrKydCl\n04q8jgKgD2l+n244r0TP7WhQa3uP13EAAIgZSiYAABJYY1unfr+zUTctKFPAz2kdiFc3LShTdzCs\np7bVeR0FAICY4dMoAAAJ7InNtQqFHUPlgDg3u3SUpo0dyV3mAABJLaYlk5ldbWY7zWyPmX2hj/UZ\nZvZIdP06M5sYfX6imXWY2Zbo172xzAkAQCJyzumXG2q0sDxPk4tGeh0HwBmYmVYsKNPGAy3af/Sk\n13EAAIiJmJVMZuaX9ENJ10iaKel2M5t5ymYfl9TinJsi6V8lfavXur3OuXnRrztjlRMAgES15dAx\n7Wk8oVu4iglICDfOK5WZ9NhmJgAHACSnWF7JtEjSHudctXOuW9IvJC0/ZZvlkv47uvxrScvMzGKY\nCQCApPHzVw8qK92v6+aWeB0FQD+My83URVMK9dimGoXDzus4AAAMuViWTKWSDvV6XBN9rs9tnHNB\nSa2SCqLrJpnZZjNbbWYXxzAnAAAJp7W9R7/Zclg3zi/VyIyA13EA9NOKBaWqaenQhgMtXkcBAGDI\nxevE33WSJjjn5kv6nKSHzWzUqRuZ2SfMbIOZbThy5MiwhwQAwCu/2nhIXcGwPri43OsoAAbgqlnj\nlJXu1682HDr7xgAAJJhYlky1ksb3elwWfa7PbcwsIClXUpNzrss51yRJzrmNkvZKmnbqH+Ccu985\nV+GcqygqKorBXwEAgPgTDjv9z9oDqijP08ySt/0OBkAcy0oP6Mb5pfrNa4fVdKLL6zgAAAypWJZM\n6yVNNbNJZpYu6TZJK0/ZZqWkj0SXb5b0onPOmVlRdOJwmdk5kqZKqo5hVgAAEsZLe45qf1O7PrSE\nq5iARPTRpRPVHQzr568e9DoKAABDKmYlU3SOpbskPStph6RfOucqzeweM7shutkDkgrMbI8iw+K+\nEH3+EklbzWyLIhOC3+mca45VVgAAEskDL+1T4cgMXT17nNdRALwDU8fm6OKphfrZ2gPqDoa9jgMA\nwJCJ6UyhzrmnJT19ynNf7bXcKel9fbzuUUmPxjIbAACJqKr+uFbvOqLPXzlNGQG/13EAvEMfu2iS\nPvqT9Vq1vU7L5516bxwAABJTvE78DQAA+nD/H6uVle7XBy9gqByQyC6dWqTJRdm6d3W1wmHndRwA\nAIYEJRMAAAmirrVDK7cc1i0V4zU6K93rOAAGweczfepdU7Sj7rie29HgdRwAAIYEJRMAAAnigT/t\nk5P08YsmeR0FwBBYPq9EEwuy9L3nd8s5rmYCACQ+SiYAABJAY1un/mfdAS0/r0Tj87O8jgNgCAT8\nPt112VS9Xndcz73O1UwAgMRHyQQAQAK49w/V6gk5fWbZVK+jABhCN84rUXlBlv7luV0KMTcTACDB\nUTIBABDnGo5HrmJaMb9UEwuzvY4DYAgF/D59/spzVVXfpkc31ngdBwCAQaFkAgAgzv37i7sVDjv9\n9WVcxQQko+vnFmv+hNH659/t1MmuoNdxAAB4xyiZAACIY3sa2/TzVw/p9kUTNKGAuZiAZGRm+vJ1\nM9TY1qX7/1jtdRwAAN4xSiYAAOLYN56uUlaaX5+9nKuYgGS2sDxf180t1r2r9+pgU7vXcQAAeEco\nmQAAiFMv7zmqF6sa9enLpqhgZIbXcQDE2Jevm6GAz3T3yu1yjknAAQCJh5IJAIA41B0M62srK1WW\nN0J3LJ3odRwAw6A4d4T+9opp+v3OI3q2ssHrOAAADBglEwAAceiBl/Zpd+MJ3bN8ljLT/F7HATBM\n7lg6UdPH5egff1vJJOAAgIRDyQQAQJw51Nyu772wS1fNGqvLpo/1Og6AYRTw+/RPN85WXWunvv/C\nbq/jAAAwIJRMAADEEeec7l5ZKZ+Z7n7PLK/jAPBAxcR83VoxXg+8tE8769u8jgMAQL9RMgEAEEee\nrWzQi1WN+twV01QyeoTXcQB45O+vma6RmQF96fFtCoeZBBwAkBgomQAAiBPH2rv1ld9s14ziUUz2\nDaS4/Ox0fenaGdpwoEUPv3rQ6zgAAPQLJRMAAHHiaysr1XKyW9+5ea4Cfk7RQKq7eWGZLpxSoG+u\nqlJ9a6fXcQAAOCs+wQIAEAeerazXE1sO667Lpmh2aa7XcQDEATPTN947R8FwWF9+YrucY9gcACC+\nUTIBAOCx5pPd+tLj2zSzeJQ+/e4pXscBEEfKC7L1uSum6fkdDVq1vd7rOAAAnBElEwAAHnLO6StP\nbFdrR4++e8t5SmOYHIBTfOzCSZpdOkpf/U2lWtt7vI4DAMBp8UkWAAAP/WpDjZ7aVqfPXj5NM4pH\neR0HQBwK+H365oq5amnv1jee3uF1HAAATouSCQAAj+w9ckJ3r6zUknMKdOelk72OAyCOzS7N1V9e\nfI4e2XBIr+w56nUcAAD6RMkEAIAHuoIhfebnm5WR5tO/3jpPfp95HQlAnPvs5VNVXpClLzy2TSe7\ngl7HAQDgbSiZAADwwLef2anKw8f17ZvmalxuptdxACSAzDS/vnPzeTrU0q57fvu613EAAHgbSiYA\nAIbZU1vr9MBL+/ThJeW6ctY4r+MASCCLJuXrk5dO1iMbDukZ7jYHAIgzlEwAAAyjXQ1t+r+/fk3z\nJ4zWl6+b6XUcAAnos5dP0+zSUfriY1vVcLzT6zgAALyJkgkAgGFyvLNHd/5so7LSA/rRBxYqPcBp\nGMDApQd8+rdb56ujJ6TP/+o1hcPO60gAAEiiZAIAYFiEwk6fe2SLDjS364fvn888TAAGZcqYkfrq\n9bP0p91H9W8v7PY6DgAAkiiZAACIOeec/vG3lXp+R6Pufs9MLT6nwOtIAJLA7YvG630Ly/T9F3br\n+dcbvI4DAAAlEwAAsfbjP1Xrp2sO6C8vnqQPL5nodRwAScLM9PUbZ2t26Sj97SNbVFV/3OtIAIAU\nR8kEAEAM/fa1w/rG01W6bk6xvnjNDK/jAEgymWl+3f+hCmVl+PXRn6xXfSsTgQMAvEPJBABAjPyu\nsl5/+8gWnT8xT9+95Tz5fOZ1JABJqGT0CD14x/k63tGjO37yqo61d3sdCQCQoiiZAACIgd9V1utT\nD23SrNJcPXDH+cpM83sdCUASm1WSq3s/tFDVR07qgw+sU2t7j9eRAAApiJIJAIAh9rvKen364UjB\n9LOPL9KozDSvIwFIARdPLdJ9H1qoXfUnIkVTB0UTAGB4UTIBADCEHl53UJ98aJNmllAwARh+754+\nRvd+aIGq6o/rQw+sU/NJhs4BAIYPJRMAAEMgHHb6/6t26B8e36ZLphbqob9YTMEEwBOXTR+rez+4\nUFX1bbr53ld0qLnd60gAgBRByQQAwCC1dfborp9v0n2rq/WBxRP04w9XaGRGwOtYAFLYshlj9dBf\nLNbRti6t+NErqjzc6nUkAEAKoGQCAGAQtte26vp/f0nPbK/Xl66doX+6cbYCfk6vALx3/sR8PfrJ\npUrzmW69b61e2XPU60gAgCTHp2AAAN6BcNjpwZf2acV/vKKunrB+8Ykl+stLzpGZeR0NAN40dWyO\nHv3UUpWOHqGP/ORV/fzVg15HAgAkMUomAAAGaE/jCd16/xrd8+TrumhqoZ7+m4u1aFK+17EAoE/F\nuSP0yzuXaMnkQn3xsW36yhPb1RMKex0LAJCEmDACAIB+6g6Gdd/qvfr3F/doRLpf37l5rm5eWMbV\nSwDiXu6INP3kjvP17WeqdN8fq7WzoU0/+sACFYzM8DoaACCJUDIBANAPWw4d0xce3aqq+jZdP7dY\nd79nlopy+OEMQOLw+0xfvHaGZhSP0t8/ulU3/OBlff/2eVpYzpWYAIChwXA5AADO4Fh7t770+Da9\n9z9e1rH2Hv34wxX6wfsXUDABSFg3zi/Vr+9cKp9Pet+9a/Qvz+1SkOFzAIAhwJVMAAD0IRx2+vXG\nGn3zmSoda+/WHUsn6nNXTFNOZprX0QBg0OaU5erpz1ysu1dW6vsv7NYfdx3RN2+ao+njRnkdDQCQ\nwMw553WGIVFRUeE2bNjgdQwAQBKoPNyqrzyxXZsOHlNFeZ7uWT5bM0v4wQtAcnpy62F9+YntausM\n6sNLyvXZy6cpdwSFOgAgwsw2Oucq+rMtVzIBABDVcrJb33tht366Zr/ystL1nZvn6qYFZfL5mNgb\nQPK6fm6JLpxcqO8+t1P/9cp+rdxyWJ969xR9YPEEZab5vY4HAEggXMkEAEh57d1BPfjSPt23ulon\nu4P6wOJyff7Kc5WbxW/yAaSW7bWt+n9P7dCa6iYV5WTory45R7cvmqDsDH43DQCpaiBXMlEyAQBS\nVsvJbj386kH91yv7daStS5fPGKu/u/pcTRub43U0APDU2uomfe/53VpT3aSczIBuqRivDy8pV3lB\nttfRAADDjJIJAIDTcM5p08FjenRTjR7bVKPOnrAunlqov1k2VRUTuY03APS26WCL/uvl/Xp6W51C\nzmnZ9DG67fwJuvTcIqX5uVE1AKQCSiYAAHrp7Alp04EW/WHXET21tU61xzqUHvDpxnkl+thFk7ib\nEgCcRcPxTj209oAefvWgjp7oVuHIdN04r1Q3LSzTjGKOoQCQzCiZAAApLRR22lbbqpf3HNUre49q\nw/4WdQXDCvhMF08t1PVzS3TFrLEalcmcSwAwED2hsFbvPKJfb6zRC1UN6gk5TS7K1lWzxunKWeM0\ntzSXmyUAQJKhZAIApJRgKKzX647r1X3NWrevWWurm9TWGZQkTR+Xo6WTC3XhlAItmpSvHIolABgS\nzSe79eTWw3pme73W7WtWKOw0blSmLppaqMWT8nXBOQUqyxshM0onAEhklEwAgKTW0R3S5kMtWr+v\nRRsONGvTgRad7A5JkibkZ2np5AItnVKopZMLVDgyw+O0AJD8jrV368WqRj33eoPWVjeppb1HklSS\nm6m5ZaN17rgcTR+Xo+nFozQ+b4QCzOcEAAmDkgkAkDQ6e0Kqqm/T9tpWVR5u1bbaVu2sb1NPyMlM\nOndsjhZNytf5EyNf43IzvY4MACktHHba3XhC6/Y1ad2+Zr1++Lj2N53UGz92+H2m4txMleWNUOno\nLJXljVBxbqbGjMrQmJxMjcnJUMHIDPkZdgcAcSFuSiYzu1rS9yT5Jf2nc+6bp6zPkPRTSQslNUm6\n1Tm3P7rui5I+Likk6TPOuWfP9GdRMgFA4giHndp7Qmrr7NGJzqDauoJq6wzqRGdQjW2dOtDUrgNN\nJ3WgqV0Hm9sVDEfOVbkj0jS7dJTmlI7Wokl5WjghX7lZDH8DgHjX0R3S7sY2VdW36UDTSdW2dKgm\n+tXQ1qlTfyTxmVQwMkNjct74eqOEylDRW5YzlBHwe/OXAoAUMZCSKRDDEH5JP5R0haQaSevNbKVz\n7vVem31cUotzboqZ3SbpW5JuNbOZkm6TNEtSiaTnzWyacy4Uq7wAgL4FQ2F1h8Lq6ol87w6G1RUM\nqSsYWT7ZFdKJrh61dUaLoq5gpDyKFkdveS5aKJ3oCr7tB4restP9Ki/I1rnjcnTNnHGaU5qrWSW5\nzO0BAAlqRLpfc8tGa27Z6Let6wqGdKStS41tXWo83qUjbZ1vLjdGl7cfPq6mE10K93HuyE73a3RW\nuvKz0zU6K015WZHvWekBZaX7o19/Xh6R7le636eA36d0v09pAVOa36c0X69lv09p/shywGecewCg\nn2JWMklaJGmPc65akszsF5KWS+pdMi2X9LXo8q8l/cAiR/Dlkn7hnOuStM/M9kTfb00M88aFX64/\npNW7jvRrW6eBXYU2kIvWBnqB20CyDCjHwGIMMHcM//0G9L4DzDGg9x7QW8c094ByDOjfOj7+P4hp\njgG988Be4OSipVH4z997FUndwXCfH+jPJjPNp5zMNOVkBDQyM6CczIAKR2YrJzNNIzMij3MyAxqZ\nkfbm+pyMgHIy05Sfna7Ckel8oAeAFJER8KssL0tleVln3C4Udmo6ES2j2jrVeLxLR090qaW9Ry0n\nu9XS3q3m9h4dbG7XsfYedXSH1B0KD0nGSCn11gLKZya/z+QzyWcmM0UfR0opX/SxSZJFvvtMsuiy\nnbosk88X+f7GKfCN941sE3lP6c/Pvbk++npx6gTiyg3nleiqWeO8jjGsYlkylUo61OtxjaTFp9vG\nORc0s1ZJBdHn157y2tJT/wAz+4SkT0jShAkThiy4lxqOd2pnQ1u/tx/oeWQgP7PZAN89Vj8PDvQH\nzYFsPdDMsfr3G3COAW0cH/9+A99XB/DvN+D3HsC2A3n3GP13fOPD50DeuP+5TVlZAaUHfMoI+P78\n3e9TRlrkN73pvZ+Pros89isj4FNWuj9SKGUGNDJaKqUxoSsAYIj5faYxozI1ZlSmpNx+vaYnFFZ7\nd0gd3SGd7A6qozuk9u7Qm1fp9oTcW5Z7QuHo47cv9wTDCoZdZNtgWCHn5JwUdk5hFxkKHln+8+M3\ntnGK/IIushz9Hn2tk+TCklNY4VB0O+m0rwu7P/+y7y3vkSRz7QLJ5MLJhV5HGHaxLJlizjl3v6T7\npcicTB7HGRJ/vWyq/nrZVK9jAAAAAAkvze9T7gifckcwfx8ADIdY/qq5VtL4Xo/Los/1uY2ZBRT5\nlURTP18LAAAAAACAOBHLkmm9pKlmNsnM0hWZyHvlKduslPSR6PLNkl50kes8V0q6zcwyzGySpKmS\nXo1hVgAAAAAAAAxCzIbLRedYukvSs5L8kh50zlWa2T2SNjjnVkp6QNLPohN7NytSRCm63S8VmSQ8\nKOnT3FkOAAAAAAAgflmyTBBXUVHhNmzY4HUMAAAAAACApGFmG51zFf3Zltv/AAAAAAAAYNAomQAA\nAAAAADBolEwAAAAAAAAYNEomAAAAAAAADBolEwAAAAAAAAaNkgkAAAAAAACDRskEAAAAAACAQaNk\nAgAAAAAAwKBRMgEAAAAAAGDQKJkAAAAAAAAwaJRMAAAAAAAAGDRKJgAAAAAAAAwaJRMAAAAAAAAG\njZIJAAAAAAAAg0bJBAAAAAAAgEGjZAIAAAAAAMCgUTIBAAAAAABg0CiZAAAAAAAAMGiUTAAAAAAA\nABg0c855nWFImNkRSQe8zgHPFUo66nUIJDT2IQwF9iMMBfYjDBb7EIYC+xEGi30o8ZU754r6s2HS\nlEyAJJnZBudchdc5kLjYhzAU2I8wFNiPMFjsQxgK7EcYLPah1MJwOQAAAAAAAAwaJRMAAAAAAAAG\njZIJyeZ+rwMg4bEPYSiwH2EosB9hsNiHMBTYjzBY7EMphDmZAAAAAAAAMGhcyQQAAAAAAIBBo2RC\nQjOzR8xsS/Rrv5ltOc12+81sW3S7DcOdE/HLzL5mZrW99qNrT7Pd1Wa208z2mNkXhjsn4puZfcfM\nqsxsq5k9bmajT7MdxyK8xdmOLWaWET3X7TGzdWY2cfhTIp6Z2Xgz+72ZvW5mlWb2N31s8y4za+11\nrvuqF1kR3852jrKI70ePR1vNbIEXORGfzOzcXseYLWZ23Mw+e8o2HItSQMDrAMBgOOdufWPZzL4r\nqfUMm7/bOXc09qmQgP7VOffPp1tpZn5JP5R0haQaSevNbKVz7vXhCoi495ykLzrngmb2LUlflPT3\np9mWYxEk9fvY8nFJLc65KWZ2m6RvSbr17e+GFBaU9H+cc5vMLEfSRjN7ro9z1J+cc9d7kA+J5Uzn\nqGskTY1+LZb0o+h3QM65nZLmSW+e32olPd7HphyLkhxXMiEpmJlJukXSz73OgqS0SNIe51y1c65b\n0i8kLfc4E+KIc+53zrlg9OFaSWVe5kHC6M+xZbmk/44u/1rSsug5D5AkOefqnHObosttknZIKvU2\nFZLUckk/dRFrJY02s2KvQyEuLZO01zl3wOsgGH6UTEgWF0tqcM7tPs16J+l3ZrbRzD4xjLmQGO6K\nXvb9oJnl9bG+VNKhXo9rxAd4nN7HJK06zTqOReitP8eWN7eJFpmtkgqGJR0STnQ45XxJ6/pYvcTM\nXjOzVWY2a1iDIVGc7RzF5yH01206/S//ORYlOYbLIe6Z2fOSxvWx6kvOud9El2/Xma9iusg5V2tm\nYyQ9Z2ZVzrk/DnVWxKcz7UOKXOr9dUU+WH1d0ncVKQmAt+jPscjMvqTI0JWHTvM2HIsAxISZjZT0\nqKTPOueOn7J6k6Ry59yJ6NyDTygy5AnojXMUBs3M0iXdoMjUAafiWJQCKJkQ95xzl59pvZkFJK2Q\ntPAM71Eb/d5oZo8rMkSBk2aKONs+9AYz+7GkJ/tYVStpfK/HZdHnkEL6cSy6Q9L1kpY559xp3oNj\nEXrrz7HljW1qoue7XElNwxMPicLM0hQpmB5yzj126vrepZNz7mkz+w8zK2R+OPTWj3MUn4fQH9dI\n2uScazh1Bcei1MBwOSSDyyVVOedq+lppZtnRiTBlZtmSrpS0fRjzIY6dMpfAe9X3vrFe0lQzmxT9\n7cxtklYORz4kBjO7WtLfSbrBOdd+mm04FuFU/Tm2rJT0kejyzZJePF2JidQUnaPrAUk7nHP/cppt\nxr0xl5eZLVLkZwDKSrypn+eolZI+HL3L3AWSWp1zdcMcFfHvtCNMOBalBq5kQjJ425hfMyuR9J/O\nuWsljZX0ePR4FpD0sHPumWFPiXj1bTObp8hwuf2S/kp66z4UvWPYXZKeleSX9KBzrtKrwIhLP5CU\nocjwAkla65y7k2MRzuR0xxYzu0fSBufcSkXKg5+Z2R5JzYqc84DeLpT0IUnbzGxL9Ll/kDRBkpxz\n9ypSUH7SzIKSOiTdRlmJU/R5jjKzO6U396OnJV0raY+kdkkf9Sgr4lS0oLxC0c/T0ed670Mci1KA\n8d8UAAAAAAAAg8VwOQAAAAAAAAwaJRMAAAAAAAAGjZIJAAAAAAAAg0bJBAAAAAAAgEGjZAIAlsGi\nNwAAACpJREFUAAAAAMCgUTIBAAAAAABg0CiZAAAAAAAAMGiUTAAAAAAAABi0/wUO7kPlFehdyAAA\nAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "norm = pd.Series(np.random.normal(0,1,100000))\n",
+ "type(norm)\n",
+ "plt.figure(figsize = (20,10))\n",
+ "norm.plot.density()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "import quandl\n",
+ "quandl.ApiConfig.api_key = 'tAyfv1zpWnyhmDsp91yv'\n",
+ "spy_table = quandl.get('BCIW/_SPXT')\n",
+ "spy = spy_table.loc['2009':'2017',['Open','Close']]\n",
+ "spy['log_return'] = np.log(spy.Close).diff()\n",
+ "spy = spy.dropna()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABJMAAAIlCAYAAABhMLnWAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXmUJUd95/vLqu6WMNjjDfucN5457YU3NjMcj23M4PHB\n9piZ97A9BoyNdwZsMHgeeDC2sQU2QgJhyWLRYkkIhNAGQrvQ0q3eF3W3Wt1dve/7Ur1VV3ctXetd\nMuP9kRmZEZERmRF58+7fj07r1s2bGRmZGRnxi1/8Fo8xRgAAAAAAAAAAAAAA2DDQ7goAAAAAAAAA\nAAAAgO4ByiQAAAAAAAAAAAAAYA2USQAAAAAAAAAAAADAGiiTAAAAAAAAAAAAAIA1UCYBAAAAAAAA\nAAAAAGugTAIAAAAAAAAAAAAA1kCZBAAAAAAAAAAAAACsgTIJAAAAAAAAAAAAAFgDZRIAAAAAAAAA\nAAAAsGZBuytQhB/+4R9mixcvbnc1AAAAAAAAAAAAAHqG7du3X2aMvT5vv65UJi1evJiGhobaXQ0A\nAAAAAAAAAACAnsHzvNM2+8HNDQAAAAAAAAAAAABYA2USAAAAAAAAAAAAALAGyiQAAAAAAAAAAAAA\nYA2USQAAAAAAAAAAAADAGiiTAAAAAAAAAAAAAIA1UCYBAAAAAAAAAAAAAGugTAIAAAAAAAAAAAAA\n1kCZBAAAAAAAAAAAAACsgTIJAAAAAAAAAAAAAFgDZRIAAAAAAAAAAAAAsAbKJAAAAAAAAAAAAABg\nDZRJAAAAAAAAAAAAAMAaKJMAAAAAAAAAAAAAgDVQJgEAAAAAAAAAAAAAa6BMAgAAAAAAAAAAAADW\nQJkEAAAAAAAAAAAAAKyBMgkAAAAAAAAAAAAAWANlEgAAAAAAAAAAAACwBsokAAAAAAAAAAAAAGAN\nlEkAWMAYo3vXH6ez47PtrgoAAAAAAAAAANBWoEwCwILzk/N0y0uH6IMPDrW7KgAAAAAAAAAAQFuB\nMgkAC4KAERHRTLXe5poAAAAAAAAAAADtBcokABw4Oz5Hc1W/3dUAAAAAAAAAAADaBpRJADjyL8sO\ntbsKAAAAAAAAAABA24AyCQBHrs7V2l0FAAAAAAAAAACgbUCZBIAjrN0VAAAAAAAAAAAA2giUSQAA\nAAAAAAAAAADAGiiTAAAAAAAAAAAAAIA1UCYB4AhjcHQDAAAAAAAAANC/QJkEAAAAAAAAAAAAAKyB\nMgkAAAAAAAAAAAAAWANlEgCOwMkNAAAAAAAAAEA/A2USAAAAAAAAAAAAALAGyiQAAAAAAAAAAAAA\nYA2USQA40s3J3CZmq7Rs34V2VwMAAAAAAAAAQBcDZRIAfcRHH91Bf/mtHXRhcq7dVQEAAAAAAAAA\n0KVAmQSAI11smETDY6ESqVoP2lwTAAAAAAAAAADdCpRJAPQRrKtVYQAAAAAAAAAAOgEokwAAAAAA\nAAAAAACANVAmAeAI6+II3B557a4CAAAAAAAAAIAuB8okAPoIuLkBAAAAAAAAAGgUKJMAAAAAAAAA\nAAAAgDWlKJM8z3uH53mHPc875nnedZrfr/E87/Ho9y2e5y1Wfv/3nudNe573d2XUB4Cy8QTvsG62\n7YGbGwAAAAAAAACARmlYmeR53iAR3U1Ev0FEbySiP/I8743Kbh8konHG2E8R0W1E9C/K718hopca\nrQsAzUIKk9TF2iS4uQEAAAAAAAAAaJQyLJPeQkTHGGMnGGNVInqMiN6l7PMuInoo+vspInq754W2\nHp7nvZuIThLR/hLqAgCwABZKAAAAAAAAAACKUoYy6d8S0bDw/Wy0TbsPY6xORJNE9EOe572OiP6B\niG7MO4nneR/2PG/I87yh0dHREqoNQP8CCyUAAAAAAAAAAEVpdwDuG4joNsbYdN6OjLGvM8bezBh7\n8+tf//rm1wwAATlmEhQxAAAAAAAAAAD6lwUllHGOiP6d8P3Hom26fc56nreAiP4NEV0hov9CRL/n\ned6tRPT9RBR4njfPGLurhHoBUBpizCTWA7okuLkBAAAAAAAAAChKGcqkbUT0Bs/zfpxCpdEfEtEf\nK/s8T0TvJ6LNRPR7RLSGMcaI6G18B8/zbiCiaSiSAGgevaAIAwAAAAAAAADQXhpWJjHG6p7nfYyI\nlhPRIBF9kzG23/O8zxHREGPseSK6n4ge8TzvGBGNUahwAqBr8GDIAwAAAAAAAAAAEFE5lknEGFtK\nREuVbdcLf88T0XtzyrihjLoA0Gy62boHSjEAAAAAgHI5eOEq/ej3XUs/+NpF7a4KAAC0jHYH4AYA\ntJBuVoQBAAAAAHQiv3HHBnrH7S+3uxoAANBSoEwCoA+BhRIAAAAAQHlcmqq0uwoAANBSoEwCwBFG\n3W/eAwslAAAAAAAAAABFgTIJAAAAAAAAAAAAAFgDZRIAfQjc3AAAAAAAAAAAFAXKJAAc6QUXsV64\nBgAAAAAAAAAA7QHKJAAAAAAAAAAAAABgDZRJAFjgCX5hvWDUAzc3AAAAAAAAAABFgTIJAAtYj/mF\n9djlAAAAAAAAAABoIVAmAQAAAAAAAAAAAABroEwCwALJza0HrHpYTzjrAQAAAAAAAABoB1AmAdCH\n9IJCDAAAAAAAAABAe4AyCYA+AkokAAAAAAAAAACNAmUSAM50v0am+68AAAAAAAAAAEC7gDIJAEe6\n2bqHh37qtex0AAAAAAAAAABaB5RJAPQR0CEBAAAAAAAAAGgUKJMA6EOgUwIAAAAAAAAAUBQokwBw\nRFXE7Dk7QZeuzrfs/HNVn5bsudBQGbBQAgAAAAAAAABQFCiTAHBEjTf0zrs20a99aV2p5/iLh4fo\n1mWHtL/d8Px++uijO2jnmfFSzwkAAAAAAAAAANgAZRIAJTBb9Ustb+WBEbpn3XHtb+cm5oiIaLpS\nb+AMME0CAAAAAAAAAFAMKJMA6EPg5gYAAAAAAAAAoChQJgHgSLv1MKztNQAAAAAAAAAA0M9AmQRA\nl+KRV/hYqKMAAAAAAAAAABQFyiQAugy4qAEAAAAAAAAAaCdQJgFggZjBrReUOb1wDQAAAAAAAAAA\n2gOUSQB0KV5xLzfEXQIAAAAAAAAAUBgokwAAAAAAAAAAAACANVAmAeBIL9j0wM0NAAAAAAAAAEBR\noEwCwIJeU7702vUAAAAAAAAAAGgdUCYB4AiDJgYAAAAAAAAAQB8DZRIAfQgCcAMAAAAAAAAAKAqU\nSQB0GWUYRsG4CgAAAAAAAABAUaBMAqBL8dpdAQAAAAAAAAAAfQmUSQA40m6rnma7qI1OVejU5Zmm\nngMAAAAAAAAAQPeyoN0VAAAUpAHTpCyF2Fv+eRUxRnTqlt8qfgIAAAAAgD4AiVkAAP1Kz1km7T8/\nSYuvW0LHLk23uyoAdCWQiQAAAAAA7IDcBADoV3pOmfT87vNERLTywEibawJ6CVFQ6NZMaPvPT9K5\niTki6t5rAAAAAAAAAADQfnpOmcTBZBkAmeGx2fhvrKIBAAAAADQORCoAQL/Sc8okDzmuQIdQ8wNa\ne+hSu6sR4wftrgEAAAAAAAAAgF6g55RJHFhegGZhalvVekAPbz5FfhDucMeqo/RnD26jjUcvO5af\n3XiLtm1fOBCvBwAAAABA4yAANwCgX+k5ZZIHwyTQBGzcJjefuELXP7ef9p6bJCKi05Fb2ZWZitO5\nAkuZxNUKLxAKhuADAAAAAAAAAKAoPadMAqBdzFV9IiLyg8b8yYImKXp8Wy0VAAAAAACwAtIVAKBf\n6TllEgyTQLMx6XpqUVCiRnU2TVMmwc0NAAAAAKBUYOwNAOhXek6ZBECzMbm8VeuhMqlRoaJZQono\n2gbBBwAAAAAAAABAUXpWmYSYMKBMTM1JbGdVP0htK0Lz3NyaUiwAAAAAQN9iE1cTAAB6kZ5TJiEA\nN2glot4ntkxqsMxmhTbyJSUVBB8AAAAAAAAAAMXoOWUSB4ZJoFmIbUtsZjVfdnMraqGUFyi7aNOW\ns7kVLAQAAAAAAMRApgIA9Cs9p0xyTZcOQFlUYsskWarwHM3lcpVQjJfrVCyyuQEAAAAAAAAAKIWe\nUyZxMG0GZWJqT1LMpEiZpO7saqFkq/NxVZsGyOYGAAAAAAAAAKAEek6ZhJhJoNmYIg9xN7cgthwq\n1hibFYC7WeUCAAAAAAAAAOgvek6ZxMG8GbQCfQBuFv1WrBHaKn1cSxezueH9AN3G6FSF3vrPq+nI\nyFS7qwIAAADEQKYCAPQrPadMgmESaDpSAG7BzU0JwM1xj5lU7n4cyc0Nkg/oMlYcuEgXr87TA5tO\ntrsqAAAAQIwaKzPezhitPzIqJUABAIBeoueUSQA0A5PyRW+Z1Bj2lkluZ0IA7vYwX/Pp6e1nocBr\nkLof3r+Fgxi2AAAAdD77z1+l939zK205OdbuqgAAQFPoWancdaINQKMklkly22tWAG7XJi4qk/B2\ntI4NRy/T3z65m45emm53VboaHpMMyiQAAACdhEnMm6v5REQ0X/dbWJvO4OCFq/RX39lJdTHGAgCg\n5+g9qRwRuEGTERWVTbFMstQmuZ5HdnNzPBgUhitBKjUIVI1QhTIJAABAhyMuIMaLeH0oc209OUYv\n7D5PY7PVdlcFANBEelYqx2QZNAuxbUkxkyJlkio0lB0zqajVHbK5tQd+233c/4ao1cP7t2gQCwYA\ngN6EMUaPbztDc9X+s2TpZsTRXVwP7OdYSVypFmAdDYCepueUSZhmgGZgIw5wC5RGlTa2SgfX00jZ\n3PpxmaxN8PbgQ6JqCLi5AQB6nXWHR+kfnt5L/7LsULurAgoiWSZFf/ejzMX1aHVH2We+5tPKAyNN\nqBEAoBn0rFTef902aAeSm5shm5srzQrAHcgmVaBF8FvNA0iDYsTKpAU9O2wBAPqcsZnQJWhyrtbm\nmgAXRAWSaIzE3dz60TA5KGiZdNOSA/QXDw/RzjPjTagVAKBsek4qR8gk0GyY4W81ZpKN7PA792yi\n7+48J5efI3Xwn90tk/pQmmki8zWf9pydyN2PxZZJuP+NwJW1CwbQyQMAehOuNF8EC8yuQpYLRcVS\n/yqTOK6WSWfG5ogIClUAuoXeHa36uecGLUNU/MTKJGs3NUY7z0zQXz++S9puq3NwbeHI5lYun3pm\nL73zrk00cnXeav86lEkNEU+yYJkEAOhR4kQDC6A071aYZJnUvnq0m9gyqeB8DBITAN1Bz0nlHqIm\ngSZgGgslyySfSdvyWqLJUsXazc1xgEY2t3LZNRxaJU1X6pn7xQG4oUxqCB6AGzGTAAC9Cl+UWjQ4\n2OaaABdMMlXs5tbCunQK/J64LqRhFgdAd7Gg3RUAoNtgBqVMte6ntmWhDrBT8zU6emmarl1gJ0Q2\nYpkEWgc3eYdlUmPUAgTgBgD0NrBM6n7khTsmffYTQaMLaf13ywDoSnpWKkcfBFqCJgA335jXBquK\n/fNHH91J77nnFZqat/QTd2zk4njej5lFyoYLh3kif2KZ1Mf27iVQiyz/EDMJANCrcAvMa6A07y5E\n+Up0c2P9a5kUFIwXidi33cvFyXkKsHDad/TcaIVOCLQSUSnDhUC1HzU1SZ7dazCaHB84f5WIiGaq\nOW5TBepJRFIH34eLZE3Dy+l0ipp6A5laHOAe97EfGJ2q0JXpSrurAUBLibNWQpnUtYgjFCzCi98D\njPXdxZkrs/TWm1fTPeuOtbsqoMX07GjVqZPluh/Q8v0X+9LktbtJntfodIW+veV0ag9uaaQ+WtOT\nrkf7D0bKiEWD4WelZmfB4jrQ+mhzbYHfdQiVjVEzvF+gN/nFL6yiX7hpVburAUBLiZVJSDTQVYjy\nmCjf93M2N76A6WyZ1IzKgKZzdmKWiIg2Hrvc5pqAVtNzo1Wnd0L3rj9OH3lkO604MNLuqoCCDI/N\n0T8+u48mZ2tKzCTZciKvLdaiAZYbtiyIViIrdUtlkqubG7K5lYrtPeSCJbdEA8Xg7wt0cgCAXoWP\n/7BM6i5EeUy2TNJt7Q/4WO0cgDsSivtRAdfN8Oc1ABehvqNnRysbq41DF6+23Lfz/GSYRnx0Cub7\n3Y7P5FYWK5OijXktK7ZMitzcFnLLpCiQdx6uA62vCQoJGic3ZlL0Ccukxojd3NB2AQA9CrdMWgTL\npK6FCeuBfI7Rj8MWl5Bd51lcpurHe9bNcCs8KJP6j54brWzb8LmJOXrH7Rvo5aOjza2QAo8diwlR\n98MYk55j7Oam7GdqkjygMHdzW+hqmWRfVSKCMqNsbF/h2DIJ978haob3CwAAegW+KIU8A90Fk/5O\nvvVzeIGilkmc/r1z3Ql/zNAl9R+lKJM8z3uH53mHPc875nnedZrfr/E87/Ho9y2e5y2Otv8Pz/O2\ne563N/r89TLqQ5Q/0ZueD4McT84lmbNePjJKi69bQucn5sqqRgquscW8srvQtSdG+sHOVlFYj7J7\n8Y6Xr0TO12wtk9wakckMGzRG3sCJbG7lwJVJaLwAgF4FseG6HymbG7dMalNd2gmXUV0ValBGdCew\nTOpfGlYmeZ43SER3E9FvENEbieiPPM97o7LbB4lonDH2U0R0GxH9S7T9MhH9NmPsTUT0fiJ6pIT6\nWO3HVw5Ea43Htp0hIqKdZyYarYaRRJnUj0NLb8GYncBnDsAtZ3OLLZOUANzVekDP7TqXUh41ZJmE\n5tcy+K1utWVSEDB6800r6cmh4Zaet1lUfS6Uo/ECAHqTJJEH+rluQnxe4pPr1ADcjDG6/rl9tP30\neBPPEX76BeNF4h3oLlisTGpzRUDLKcMy6S1EdIwxdoIxViWix4joXco+7yKih6K/nyKit3ue5zHG\ndjLGzkfb9xPRazzPu6aEOuWSWAukO6tWTFZgmdT9sOg/FVtFYc0YM0lWJt226gh9/LFdtObQpfC8\nBYWTfja3bga2/URWX9NMqn5Al6er9I/f3dfS8zaLOlbsAQA9Ti1WmoNuRZQB45hJHfZEA0b08ObT\n9PKRckN9vHL8Mn3s0R3EGIvvg7vsCW1EN8KN72GZ1H+UoUz6t0QkLn2fjbZp92GM1Ylokoh+SNnn\nd4loB2NMG5na87wPe5435Hne0OhofueX13Xxvk3s9L0WdGADcZaCzhpYQAEMfm7qozW1qnqczU2N\nmSS7uV2MgrZzl8yiLUfO5pZfCtpoNtYxk6h/YyZdmJyjlSVlrkTMJABAv9Dq5DCgMaSYSaKbW4c+\nRi7fle0lsfXkGL245wL5AYsXzYsupHXorQMGuNLQ1kMI9A4dEYDb87z/SKHr20dM+zDGvs4YezNj\n7M2vf/3rGz5n4ubWcFFOJAG4W3te0Bja2EimfS2fLc9OtSBqFIscA3DrajA8NmuM+SVnc7MoHW3U\nirz71C7LpE7g0S1n6KPf3lFKWfGKff/dRgBABzBTqdOV6dZk4kU3172Ii3Wdms2NV6dsuSRWIDFG\nunAiRKEia+vJMeOCJXQR3Qnc3PqXMpRJ54jo3wnffyzapt3H87wFRPRviOhK9P3HiOhZIvpfjLHj\nJdSHiFwmeOmJu0unX/MD+qfv7qVLV+et9h8YQMykXoExNyWTSi2Qg9WZYiaJ58v6TkT0tlvX0n+9\nZY32eFehAW3Ujrz7FMdMavESZVytNj7G+ZpPtZICjyfZEtEuAQCt5+1fXk+/cNOqpp6Dz8P6cO2h\nq5HEAMkyqTPdFpmg9GlGwWJMUVX23HFmnH7/a5tpy8kxqzqC7oA/Zri59R9lKJO2EdEbPM/7cc/z\nFhHRHxLR88o+z1MYYJuI6PeIaA1jjHme9/1EtISIrmOMbSqhLs4abamTK9D+1xy6RN969Qxd/9x+\nq/15/SAodD+MmD7Lm202t2hyPBC9hQsX6N3cTM3StQlJ2dxsLJMcy+83+D3MvU8F4gYs2XMhVlA/\nMTRMR0am3OvXAU+w5uvfkWJlIWYSAKB9XLRcNCwDuJl3F5I1kqhMii2Tsp/n8NgsrY3iYrYCXt+y\n3SlF17Y4m5tyjplKKOMeOH9VWwZUEd1JnM2tI3yeQCtp+JFHMZA+RkTLieggET3BGNvved7nPM97\nZ7Tb/UT0Q57nHSOivyGi66LtHyOinyKi6z3P2xX9+5FG60SUP5FKtPK6Yx3Oo4m9lAWyufUOoWVS\n+jlaWybxbG6eHID7+OiMdv89Zyfo6nxNOn+l7tO3t5y2EghcLZPQRO3ItYKMPnVWkDqmK3X66KM7\n6AMPbCMiohuf30+Pb3PPyMYfdzuVSmVmJuJuoWiWAIBexUMohK5H5+aWx9u/sp7+7MFtzapSCt6+\nyo7lyOc2ATPHTOLfjl7KWyTDS9BNwDKpf1lQRiGMsaVEtFTZdr3w9zwRvVdz3E1EdFMZdXAl8eVN\nJnitaP7clxTBFbsLrQVS/D91X0vLpIBbJskxk/aem9Tu/9Dm07RzeCLO/saI0b+uPkZ3rT1G33vt\nQnrnz/5fmeeTYiZZ1K8TLFu6AzvFta3QNlcNV+34KnjAEqscp1p1wGwkVgCxxuMgcOUrZlkAgF4H\n42+XYbD8trVIrlrHyiyXZlkmBQEZs7lx2eTIyLS2DOgiuhP+XBGAu//oW2O0xJe3tecdjC2TWnte\nUD6M6cU927kuj6GjxkzKYs/ZRNHEGMXBtm0EESmbm0UlO2nO/tv/upHedXcpnrClk/cuxwKVZcyk\n+VqoTOLKxYCxRJHiQCc8Pq4EK8MSs4psbgCAHodnFYaM2L0wIvqNOzbQPz671zkA90ylTk8ODbds\nMajsmEliljjTQlpsmTQypb1O/g50kgwK8ond3KBL6jt6TpnkWdoX8T5KN8lpZifuwc2tp9C1FXs3\nt3ByPOigTArPmfw9H8VXunZh/rGlB1psIXvPTdLu4Yl2V0OCP3vbYP+2lkkz1ToRES2KYmgxKmiZ\nFMjnbwdxBrYSy+ziZgwAAFagn+suxMcVBIwOXrhK395yRgjAbfdAP/XMXvrkU3uMFupl0awFddEa\nKVYsqbJP9PXqfJ0uTaWzI8aunuVWra1MzFY7wlq8mXBHn0FYJvUdPadMskUXGK4VpnncCqXXO5V+\nQMxWoW4P/8g+nisXuJvbNRYKIek8lLhEvWbhYO7+kmWSTfloolbkxmeLPm1jVvHglNdEyiRiSbD2\nMuvVCqolWiZx0HcCAJrJfM2n53efb8u5kyQt2f3c+7+5lZ7afrYFNQKN4GphduhiGJTadnGxKLpQ\nH6WUy93chJhJacuk5HtWcpFeGerHZ6r0nz+3kr6y8ki7q9JU4j4LuqS+o3eVSXnWAtFn2cHn8hhA\nNreuxGVibrtvnM0tahMLNbahk7M1o1DJGKO5mr0ySYqZZFHFTlBGdAP5lknhDq4xkxLLJEa1Ah1G\nJ/Qx9ZIysIkKpA64LABAD3PTkgP0f76zk149caXdVTGy/sgo/d2Tu9tdDRBhypbr6uZ2ZbpKRMn4\n3yyaZ5kUfQZ2GeN0cZN6zbCFexA8sOlUeyvSZHibQgDu/qOUANydhG0bjrXnomVSE+qjwq1QOtnN\n7cp0hV6zaJC+Z1HPNY9SMQUVjh+t8tt8zSfPI7pmQaj4ibO5xQG10/zs51Zk1mG+FkoCCy0ED9cF\nqA5uoh1BlqusDtsVwJSbW1HLpNi8vn3Ebm4NVqIuxftqrCwAAMjiwkSY/GB6vt7yc8eWSZ2wGgCs\nERffxL99V2XSTNVp/6K4yi+26LK5pSyThK9HsyyTemTpiCtXpiut709aCX/2cHPrP3rWMim/C0r8\neluJ1wWWSb9w0yp6d4cGO+4kGDG9m5th/5/+zDJ6+5fXx99rsWVSsY6XsSRYs00zloUG2zcE5FF2\nzKTYMmlQjJnk/jQ64fklQbMbq40YYL6TFfEAAFAGWb0cXH07G3Go9wsu6rQsAHfJkxE5AHfyt7xP\n+PnaRYNaNzfb2LfdQr+8rrytQ5fUf/SMMmnd4Uv07rs3WXeMiYlnev9mvvitjpl0+spMoeC9ppSd\nIIEx/SQ5fraaR3x2fC7+mysXYsskyyaRhGRK3Nxs2pOvse5Yvv8iveuujdpVUAis2dg/Lx6bwDJm\nUsoyiRV6h7kA187nmGRzK6ccAJpNzQ/o8nQ6KCzoH9o58iXZ3My1KFsBABpHdnNLvhS1MDMdFQSs\nlDE9jhtbQllHR6ZoJrK6kdzc+EKashjGv73hR7+Xjo5MGy2vxapNztW6Vg7oFQurPHhbb0X8YdBZ\n9Iwy6ROP76JdwxM0OVcjovwJFP9VDsDdrNolDFgGVyyDK9MV+tUvrqMbnt/f9HP1OiYLpMwA3BGm\ndqVmc3OtjGiZZCOv6ISGIxenaPfZSappXLD6Y/hrnKKWSX7A6PZVR+jqfE3aPqsE4GaUFsbsKiZ/\nPX1lhqaUczWbWkkBuOHmBlrFp5/ZS2++aRVVojgXoH9p55woq59rdaxP4Ib4dPyCizqm3X/i00vp\nQw8NFayZUH706ReRLcRyGKP/cdvLcZ1kNze9worfi1/5v19PU5U6rTl0SS5Uk83tN+/YQA92acyh\nfpFZ/HiBvM0VAS2nZx4514TargJkWiY1cRrNLZNaIQtMRIq1zcc7N4hkJ7D//CQtvm4JDY/NOh3H\nmL6lqEKDaSCpx2nT5c88KvUkqDF3ibI5VpfNjcW/pffvlwGwKHFwSVvFtSK0Hbs0TbevOkobjlyW\ntnPXMM9LLNbqBTKuqH3Mr35xHb333s3O5TRCrZ4oPhtBbrtomKB5LN17gYiKuZYC0CixPJDRaXar\nhUYvIz4t8dHxR+Xam2TJFatV5UsGT28/Sxcn51Pb4zlQg4MzP3xzFKw+lneEmElqvEi+z1t//AeJ\niGhYsNg3MTpVoYtX09fRDfTLSBJnqIZlUt/RM8okbvGTrAJk76/z5W1F8+cTxFaYKfNrxHudzRPb\nhomIaNXBEafjQssknTLSDm4NxJuC7Zg+JQQFna/bSyq6bG5iGtcU/TICZrDt1Bj9+YPbMt/XvNuU\nZZkUbtdPDERz9mqhmElcSZlw6KI52GUzqMXZ3BprTK6ZCAFoFLj5gnY0gQwv+ZhClqqgZWjd3Bwf\nWRltb3KuRn/75G76X9/cojlB+FF2oPc48QdjwqK9uk/4OTCgD/vhxfsJ95GxQolIQOvwoUzqW3om\nXZezZVJHa1mdAAAgAElEQVT02WpzYa70aoWgyi8N/qvZFL0/jJFWA2n7aLlA6OoCdJW7cpIwcFsc\np7U+yghEDwsQov/9rR10ebpCV2Yq9CPfe630W6KQy75Psal3anUu3K5aQPA+LBCEsWLZ3JwPKZ04\nAHeDdfE1VnUAANBrZC7wROjc0kF7EeUA8ckVtfwpQ/7issSlqXQMuCzZzwX1aN40/UCIy5Rqr9lK\nB51MHjBGtS5175TaBmM9OydDAO7+pWcsk3jbtV0EiAfsJgbgvjxdSZkj82DLregTuTAygBfbiqzn\nrv9Nf4C61fP0ygC+jbdB2yYxFQU6ZIzFwTpt2mwgCTuyBZ/Ne7Dv3CR9ZcVhy1p2Dhcm5+iWlw4V\nWoFjLFvoIbJ/bqb0uGrbiE3DmaD0LrASnQTgdj60NMqKmaQLHg8AAM2kHZMidWzWwceDQQh3HYn4\n7OJx2FE51KpxrlEvCXUxTRszyWCZxGPr2MgHAWs8vlO7EC+vUu9dRTB/PrBM6j96RpnEG6+Nlv3e\n9cdp68mxcH8pAHd5L0AQMHrzTavo757cLW1PlF4tsEyK+iy82Ha4PhHG5EEiy+psXjOA1GILFMcT\n8/NLf+cXkjUh1wkUahtdvv8i3bnmWNe5f/zN47vp3vXHaefwuPOxgY0yKS9mUixQGZRJgUEYE9zc\niqxEd8JjqsVxwRpDtkzqgAsDPUscq6yNdZir+vTmm1bS+iOjbawFaAeJZZJ5nyxl0t8/tZtufulg\nM6oGMhDHW3GMihcLHTuUMsbvLLkhK25sIwRCubxkU8wkMS6kSOLmxj+Ly0GdBlcmPTE0TPe9fKLN\ntSkXLstixtl/9IwyyXNwH7t77TF6Yc95IjIE4C6hb+VKrRf3XKDhsVn61DN7QwuEFgqqzZp0fea7\n+2jLid4J6l1U16ZOk5NU7ul9edY1kbpiteHc7hjFvbaNPKBTYMaDvUXsp7JclloNz8pUpN5Z95X/\nlB+fLfxMWSZFJaiWSbE1UhDEf3drwNWyLJMkq7oua3+t4oltw9pAq6AYrI2v3PHRabo8XaVbXjrU\nvkqAthCPKxnyG59UL9Aok54YOktfW99bk9RuQ9R5cGMad/EuOWLD0VEaKRB8+i1fWJ1RfkjDlknq\nd0GeDUyyT/TVlJAons8pVnrdGitMtkwK5dGley/QMzvPtalGzaEVRhKgM+kZZdKAEtg6q03X/CBe\nLRAn0WVqU8Xz/92Tu+k7W8/Q1lNj8Q+tsO5QO+wy8ANGj7x6mjYcvZy/c4+jWiYNxopCjWWSVpmk\nt1ixPj8xbaBCE9q4MxmKLHUbz8zlOmB8ZcVhWrbvgtMxzaDIaxBkvK82gVLF39XnbBa0knbRiBDV\nCQN7rWgqG4Uu1aW1jPGZKv3903vo/d/c2u6q9AztfH9cFsdA+bTzvifWGOZ94ObW2egsk1wRD3vf\n/VvpnXdtbLRaErokREREFyfn6cJkfna1pBzle/TpM2Y8B78/A4rSiKO2an58kay2nYB4fZVasijL\nFUut4sFNJ+nutceaVj6XZbs0tBVogJ5RJnHhy2bSUfNFX97mtHqx8xxI1OyZqdibVYeBEp9ybOXR\nRa4mfsDo7rXHaKZSz9wvS4DUXS9Ttg4YTHaJiOZr6QeuWvo04lNvc6Ts5ibbVWkt9JRSEysTp2rS\nE0NnacUBt0x5ZdJIS7VxOShsmRQLSKqSKfxe85MWViRNudQ+2jQ5qsVB5hsrR9d2u4W6H9DUfK25\n54juz5WZdKBVUIx2tjIPjgIdQXsiBOQvOPKxWGeZpGPj0ct0w/P7G68aMCKPt8nfNgvc+vLkA0au\nltu3m2S/t968mn7p5jUO5ejlFzmBSLZlEmNEX3/5OK05NKLdj1exiBzUafA5VMAYVVscP+mGFw7Q\nF5c3L+6pHyTPHvQXPahMiiboBlHQD1j4z6AxD49tHNHX1xNckZLOsfkvW6B02GXAterdpHlesvcC\nfXH5YfqSIXh0UcFdtUyiRGeYIssyKUi0SW7nN37Rk/XMtEpV1TKpoMtSwFiHCAHuz1lMc2si737w\nvkhdoeTfjAG4RcukAtrndruG8b6WqHHlc7uvpRE+8cRuetMNK9pdDWBJK+MaAqBiFTMp4JZJdiL8\nn96/hR585VSDNQNF4HMN58XCZlRGLJ/LGSWfiLfbzcev0Iajo9E59CcRLTAf2HSKXtx9Idouy2qx\nZVKXmiiLlz8vWSZ15/WY6FY3RNA4vaNMikTAes4qQDwhjt5hqfGXuAqls0xiJJp9lneuvDqUGVic\nd37dJGdzRc7UvN4yqZHbIwoIatBAEr7rBg2uIGgkNavoW26bol6tm/E35XvRmEkBI6o1adB8YNNJ\nOjs+q/1tvubT2Ew1tX1yrqZV7ukImPwpY7fimGeZpCra+P41P0j+LnD/xFIbTf9bBDHOU6mWSY0V\n1XJe2H2+Zefqpn7ZlvmaTx94YCsdH51u6Xk7wc0N9B+81WW7ublZJoHmI7m2CQ+veADu8vqfrKLU\n4NiNls2v/YvLD9PVSOZOJR+JPrmbJmORvJNTtipDdQtirflcoB2WSc1GtErrdlbsv0jjmvkD0NMz\nyqSB2DIpuxGr1hX6CbbLi6DfVyxXskwqdI5iJKak5ZWZBDN2q//YTJWuNtnVo1FuWnLQyYdZtUzy\nlJhJsp90utw401Uxw6SUWXVe29dlc4utZnSGSSnLpGIDBWOsKb7uU/M1uvGFA7R0rz4e0x9+/VX6\n+c+vTG3/2RtX0G//q138AZvBMW/Fkf+aymgiWCDJ21m8PXZzKyBEiVVux+AuKpMa7e/qmrYLGuO7\nO8/RszvPtrsaubx64gqtOzzaejedDmhnaOvtoZ233RRnRqTWpphJ05U6HbvUWqVuNyK5uRV8iZv9\n7nPZomxjH91Yb5JxxADc1XoQbzfFTGpnIpKX9l6gX/3i2kLWUeI94XOBXlQmcTm/25VJV6Yr9OFH\nttNHHtne7qp0DT2kTJIDcJusUGpK0GOxkyvi7mR6Z3ixjBIlg+hD3Bo3N7nDbpQbnt9P//D0Hqls\nW37+8yvpF29aVUo98nhyaJg+9uiO+LvL1R+/NKPdrrvcVNBAT78vo8SqR6TRjjcMwJ0Mxnn6hizL\nJKuYSfVi9fUZo2oTzF/nc1wudw1PEJH+2R21FIit3te8S+Mm2obVOTXdbSDsn8QcaEyAacfYLlpc\nNXp+yc2tE2b5PcBfP76LPvH47nZXIxc+Yc7rd4KA0Qce2EqbjzeYadQhQ6YrO86M02w1O3YfESyT\n+hmbZsdlhwWDYUPZcWacPvDA1qZPth965RT9zj2bmlL2vnOTtPi6JbTzzHhTym820uKesD1x9XYs\nLy638Y5I259w2abkjk63bmha6BS9NsIYkTL8e5yspI1uVNc9s5dOX5ml6ZzYqyJT8zW6eelBSf6v\nCLFHWx2Au9kUjQ/23K5zdOzSVBNqVAz+vE6P6eeDIE3PKJM8xTLp6R1ntWmSVcukRvsmYz/MlUlM\nsAwSLJNa0Sfye+GyeJU1cD34yil69cRYtJ97fVrlH/zJp/bQi3vss4cVldtTlknxdr664sXfdTGD\nVMWmq9DAmOxzrjOtFpFdheTfsxRNSX2LxcsKAtYUNzcxkKENjWVzS/9mE9uCSLRMUu559N0UnLIe\nBJIw5ZosQNy73ZZJ/7rmKH113fHCZems6ppBIMR56iZ6WfnAs2TmGTfO1Xxad3iUtp8eK+W8Zb8z\n+85N0nvueYXuXG2fTQeK0/bQztfJZgEjzuYWvRs7z0zQusOjND6b7ZbRqGLi6lzNaTLtwvojYXyd\ndibraATxzor3OYmJ6Xbvi7rHqcebykjmIo21ifTiabbsKR4zICzAim79iUKfSZ9FLLTLwtb7ReS2\nlUfpay+foKeGEgvg+LlEC8DdGgdKRxKA2+24jz+2i/77V15uQo1Aq+ghZZIcM4mItOktq3V5Qqzz\nF3Z5D0wDvi5mUmiZxDKPKxPeablYXNlWq9PmWx96aEjr0nT7qiP0yadCayrTtYkTMfcgiflKGCLS\nmrPWC8YgSs4t/y0OcqqAECqb0nU0KTrU8onEmEnuSq9mrJjaxu9qpKlmKpPizxyLCW5ppCqNos+U\nkklYhRPvtes9lJSLbXhfxTa/+uAlWnv4UuGyZMG4eRfzwYe20U9+emlTym5GvTcdu9zSmEztgI/t\neZMe/mtZrgNlj9Ero0myTf2ShYhSqwAKcuzSNH3i8V0tOVc8rmQ8ez4WJDFnwp3nq9ltq+g4MF2p\n0+dfPEAz1Xrz3a86vM0/t+tcbvw2aSEnSLYFAaM7Vh21isWSLCQVuyG5/SVXWjYoHKQXJjV1SVll\nR3MTYW5UDzSSFJdT4xi37VO88HfNRfnGFzzFeWkSh5NF+/SOMim5zg5/iUHpdK0yaXSqIqVb5voA\nsdPS+ZPzCbHWza0By4Ws7Ul2mOT3VsRM4p2ey3XZDlydtmK66uCINtjy7auONu2cKcuk2GQ3+l24\nRzpFQD3W4hdcgVLcmMRnZ1JQmIqwiR1W2DKJsaYok3gQbdt3qchqszrw68hVZsWKa/WZRKttqWxu\nkfJJEa5cg0+K9Wq3ZVK1HjTUBkQBrplXsvbwaNPKbsYj+JNvbKG/+s7O8guOWLLnAv3pN7Y0rXwb\n1AmzCf57WS61ZT+v+Whi8f3fszB33162NOsG1Ef/T9/dS8/uPNeac1ssOCbZ3OSGMpeTWKKo3HnX\nmmN0/8aT9K1XzzRUThZJmvjOki1Vrnt6Lz2+bTi1XXYr1y/sbT5xhW5bdYQ+9cze3POoC36u5M1t\nuHSRJVeMz1S1i/JZaGMmpRY3o3pFdavW5YXKJHwDk+vaApeO8Zkqnb6Sdm9K2qd9WbpdfUXu76W4\nSfG19cglFc303Y90rTLpF7+win79y+vj72rMJHGbSJLNrZxGb+pYxP7ZEwbJZDWgsfPawAcJl5hJ\ntv1kh4/3WkwKsKLZ7lIxk/h25TSMJUpM8VQpNzfn84sKEia1KVUQVb8ngor5PUi7ueULuToCls5Y\nVgaVejHlVhGyrjnvfvBfU0Jb9DXt5sYFp0B6Bq6rcuKxrA2Du3i9Fb9BZVIXBuDecHRUEhSbWe1m\nKQs/+ugO2njscqllMsassykS2bsX8F8bFc5N/Xij8HHYpX5d0tR7Fj6Z+IHvWSRt33KiwbhcFmQ9\ne96X8phJ/P3PUyYVHSvVsWd0qiJ9vzQ1T7cuO9SQlUvs8lS4BDe2nRqju9eaXU5vXXaIPvTQttT2\nqh/k90XiQo7grsa32ySjadSLwXbMzLqWX/zCKvqlm9dknkct28oyiSuTvLBfjK3M1bKVMtX4ks3g\nv315Hf3qF9eltuvmmHnEyjEvvY0X00uWSaqirFvp8uq3ha5VJhHJA5oaM8lErS43djHLVDHLBf35\nRO28nM2tdS8bH8QGHJ6ytWVSD71t4nN3WnVg8v5x/CJlSGSUZG0YFEaVegFLH3lQEhWV8uqP+h7k\nZnqzuPC6Em/MlmZZJlVqxepTBH22OzslYGKZpGRziz5NgbnrYvpHclfIyW5urX9fxUlztR7EfW8R\nui0A944z4/S++7fSl1Ycjrc1tc9k0kdH8+UVR+inP7PMOvbKQOxekL0fv71Vv5ygpmW/M4lbQ379\n1Ph7oL384GtlZdIffP1VqvkBzTQhflC80JNlmRRncxuQjpmrptsWK6HvVI96yz+vlr6vPXSJ7ll3\nnIbHZwuVTySEgyigkLpz9VG6fdURp2M+/PAQfXH5YRq5mo6tSkR0z7rjtOqg7JrtRzH1stze1b+5\nbMUYo4WR8s/GwobvkdUFTGUopazd3EQ5Qbn3NtbQ6h66fjPt5hbiRerauE8UlExiWaZQAc1gYlZ/\nT4vETNI9ArE9EPWmZZLLU+rEMS5unzBMsqarlUkifCASlUO6Ti12c4t+a1YAbnF7EmROzObW2Hlt\nKGSZZFmvTouZZEXJdWakCmd6M1jG0jEOiJJtsVLCon6DhmfpM0Y3vXgg/q4u4KQsk5Q/tDGTlE3c\nfcS172+aMikOwJ2zYwmDVeaAx0JFm0nIMJmT6xTa0naf5bpK2tJuNzfddx0XJ+fpDf+4lIZOyUGU\n6yVmhmsFY9Ohy+0JIbZGM6vd7FtSZsafJ7eHLiLThoyrKoO2k0yuTCpJOC/7njKH+nktttIA2fzQ\n665JbfuLh4foP352Oa05NFLqhIj3+TbWJINKO9FZ/LXCqpNnVm2kfHHR1ZWvrDziHNLgJ1//OiIi\nWucQyy+W2XLeTK1lEhEtGAynXLrsvqYyTPf05SOj9KYbVtC6w5foTZ9dTkv3yklnxP5S7+YWIrYP\nm3ql66nKNel9UgtmgsWO5wnxL3kspXg/XiaXidqneOGLGi7hBni9RXcpNUh1L2V0U0N32NCVc0mQ\nomeUSTrLJHElf+2hS3Tp6rzg5kbRZ84SQw4uAbiZUHQrtLFxAG4HZZJtJ9DtZoyuaFeimLxClTUB\niM3SJWUSV2ja38sB4XjGWDxE7Tt3lZ4RYjqoZabNjOUVBF17VAUmNROiLc12c7OVYIu6MxJlD3iM\nGP3M9cvo17601rQDEZlNvdXVtkDYXzzEdVWu3QG41WduY6K+//wk1XxGN7ywX9ouWyZ1PkmWxWRb\nUw2TmnxTyuzvRRcHG2ytjnl/1akBuPl4bOPW0GfDqxV1P6B/+u5e5xguRVDv//dduyC1z7oovtqf\nPzikjaHT6LltXKtFy2QivZubHPy3WMPKOyyOX1io9BAxGHMreMOPhsqkNYfslUn8XurlweRvKX6l\nsFi4KFIm2SysqPGCVLacDF0tX9xzgaYqdbr5pYPauprrm574l+FypZMl1XmW+M0T3NyW7r1IH3po\nSMpSHH6G313jRpZJ4ubm4KasGetiJSHZjwfdgp/xfuQdA7qbnlMmiZ0N12LX/YA+9PAQPbZtODUh\nbjQAt2n0lDtLis9pIyiYuP65fXTXGvvVFz6IaeKQG7GtVje+/kalTUEdg640z0sPpowlExxRGcQt\nUpKVq/y7KlomiXurE6h0Gnp9eUzzHoj1FskKwP3k0DDtOTuhPUfAmHbF68TodENKVS7AWhosNAR/\nX9ccGqEzV2alcoMgVJwMj+knOXw/szub4v4WnasWBNL9cY0XYBJuW0XKMsnCze01CweJKMyeJCIW\n1a0T7Wa65zX7+TaaPlqEl2Tb7doEwScS3dzs35P7Xj5B964/biiv8Wt+cmiY/k8UIN0lRgaS4qQZ\nHp+jb716hjYcLTeGl8hMpU7DY4KrlkYprOPseHkKLhvrdf5bktwl3KBzc5MU8U1qT/MluJy7yKll\nwGWejUcvW1uH1JRA0SbEn8XuiIecKMPNjZcbxHK+fAPzLDl1Cpoiinj1LLr6muJFel7YhsXzrjo4\nkiq7M5RJ4afLwqhuTzVIdS8qk2xd2Ik60zAhCQQPbOkZZZIuOBr/e6bikx8wKaOQnzWJdpDgjJZJ\nkpIqWT1KYiZZnyLm1RNXaOcZ/YRdB782lxeil2MmmQbKohH7w+cpf/dI4+ZGiYuY6OZWL+A2NihZ\nJiXbTa5SnFQ2DaVc3WRRLYMLUjoh5ZNP7aF33rUptZ1bb6mKhV3DE/TrX15PD75yKnWMLUkA7ua3\nRX6Ojz+2ix7efEr6Le/sJoWdKQ6AaN4uPhdXNzex1GbdowuTc3Tv+uPa/kCd1NvUvxpb8MlDk5zN\nrfP7Hp2VYlMtk5pXNBGVmzAibisZ3a6UDSmwe8+LZMdZdXCElu27aCjPuhgjn3xqDz2/+7xUv9UH\nR2jxdUu0GYM4satTwfPOVuv0lZVHmuJe3C74/XMJ3u7K/RtP0nu++kqywVKRWarlnoWbm6kPnNco\nRcRxp7BlUk5L5Od1LT4IGO09O0lEsmKsUvcz4wGVAX81Zqo+7T9/1eoYvqCjv0z9GCW6ufH7Y7Mw\npLMcEvtFvljON6nKJNsFALF9FHG5Uk+ja2NZ7U7M5hZv49ncFLcp2/6MMVa6xUscu6+Qm1t6Wydk\nc7swOUcXJ/Uxw4rA783KAyO00VLp34mWSV04vW07PaNM8jTKpBrXklZDLWnAGFXr8kBt2+EOj83K\nK1YRpvdALHZAMN9txDKpUg+cVoj5vbCJmbRi/0X639/abi1At+tl+8aGE/T09rOFjq3WA/rGhhP0\n9i+vk7YX935iqUm053npANyMkZpFkIhSik2beyqu3jGieJRSB1mT4kI+WFgF1WVziz63nRqjtYcu\nFYqZFK8oKQoTPpHa4aAcVXHN5taIwM8Pna36KVN3sQ3cuuyQ8dgwcKdQh1iwND8r8b51opvbRx7Z\nTre8dIhOX0n3jTVFSLKxGKlrlK5EigKziwZ6G6X7uYm5hif9tivmRSlzsmxjdSNb1YWfttncXFZ6\nGUsrJ1TXoTzuWHWU3nNPWpGePldY4NUoVtT20+OZ9WqEO1cfoztXH6Unh4qNlZ0Iv38665uymJyr\n0fhMNSUT5PWfZfavunHFtE/y3XxvpJhJFGZeKypDmUjeIbcb8dDmU/Tbd22kV45djifrjBH9/r2b\n6U03rCi1jipinzZbsbRMypCBpG3C32rA5bAch5hJhnNwOSReNFbarCgvqL+NzVTpxsiVXBxbTYoN\nP2D0c59bQc/syG83urEitWDGYyN5XpTNTX//+VGuAbj/9ond9JOfXmq1ry3cK8DJOkqza+y+GP3W\nzphJv3TzGnrrzavzd7REXNTmbph5lGn1XBbxeleTInCvPBAuKOl0Ct1KzyiTdJH2ueaeB/r0Wdrd\nxjaw6NtuXUtvu3VtartNzCRdquFCyqRa4CS0JINM/gux/cw4vbTvovWkpl2miY9uPUMv7buQv6OG\nSj2gm5YcpOOjGSvCJuWgZlRQLZOIMiyTNIqPIsHqTDGTqooLUdrNTX8OvlXXofNN7713M/3Zg9sK\nxUzi5arvXRnxESo8ToO1NV3hU8XWVSmFEMlt4J51aZcZ8XdZsOfCoGpVlvwtvo/Olklif9MkbdLV\nuXD1WFd6KmaSRf11scWI0hMiV0auztO77tpIl6bKW4VzhbHQYmTHmUSJMDlbo1++ZY0UPJ/IzUyc\nqPmm8qW6ucUrsxn7iOe2jMPAf3dZ6WXEjPfOtm+6bdURK6W4yyuYTDiK3ffpSvhe1oOAZqt1+pvH\nd9GV6UrOUZ0Nv3+6uEBl4QeM6kHaqiHfxbLE90P5tDkfr25eAO6nt5+lDz44RH/75G667NAe8i4v\ncXOzLpKIEnfm46PTkmXS7shaqZnIC892fUbN0hpavA+6rKo2Lt+xhZpQNV18I6Obm2TRJJd904sH\n4kx1Yt9uWvCZrtRpfLZGn31uf/pHpWxdG0glgOGT9eif2gerwdjjRUnL5yTGDy2LIjGTkthm4jb5\nt17K5ibeGltFTLNk00Zo9vz2qSgJyd5zze/nWkXPKJN4sxW1xnwywwVzxtKr5Tots5vlRb4yKc7m\nJliyFHEbqPqBk9CSWCbl78tfaFNazNT+bXr/J2ZrhZUCNp22SyfCKN1WPM80sU4LIUXc3FSBgXfY\n6kQ9z83tzNgsvemzy+NsU/rr1isD3DI1sPhYse3GV9FAO0oygGQjrvQWHbgCxoxBRtV3Us04Ij1z\n0eUg2k1Vuoj7i7+5xwswC5MubD05Rh96aJvBJThE18WobdJmVZFbaamWSZKbW4GLeWTzadp9dpIe\n31peoNwsdK6zjBh9/LFd9J57XqHxmTDb20ik3NpwLDEJ33FmnP7TZ5fT4uuW0AObTlqdz1YgHZ+p\n0gObTjrfwzIFPpsYSFIAW74Cnzeh5wG4HZSuATNbupQegDtlxWreV2eV4IIvvEePbxumZ3aeoztX\nu2W7aiUnL8/QRx4ZynRh4/ekmZZJqXTdfFKb0/5LbSsW70d6DAo/Z3Msk2584QCNXA37nDLTrCcL\nO27H8Rh587VAWGAqrVqZ+BpZTLufuECd4ebGpL/FcV5UJsnlZJH0AcLYJ/weW7Yb5PwsS06xjxSr\nkqvk0maFUxVF6TJM8SI9L5RpKzX9/VBd/Wp+ejEvj0tT8/TinvNOx+jg/XWRmEmiYiVeHIm+tyNm\n0u999ZWmWESJ7do1JmIn0ewqcfmwl2Iy9Y4yKTNmUuTmFqRTlEsBuAs8WtOLIG6P3dwCQdNeoLlW\nar6Tf2kSgDv/uvhtmZitWpXt0p+XNREJAkYTs9XCL7qp89T5M9sQ7qpMEMhL3xuWHviJ0v73NoOk\n+CzF3fPc3NTvp8dmaapSp+EocKjuGanVyQrAbSJR5Mh1SDIcZhf2yvHLRp/uSkYMJ21dqLiFRRjH\nQY5RoGYa4UzM1aRJkfi7zsImle7W8FxVRXh+neX6F+XDjwzRqoOXtH1DYg6cPk6d1NeDfGUev8ZM\nyySHS/EDRouvW0J3rT1GRC0UXHRCNyPaPRxasPB7w60DvvfahfF+uwQrF9tYHraC4coDI3TjCwe0\nbolZNHLflu+/SIuvW0KTkRWbGjNCh+6dyW3D0c8uK70BY9o4M2odykC9h0Vj9dmQpI73BMVS54p7\n20+P0/L9I3RuwhzIOg4y3UTLJP6MUhbsOW2hVDc3i5hJ6exYsqwroo55vK8+emmqgVrKxDGTHKWz\n1ywKlUlzNV8YQxq7mWfHZ+nnPreCTl42W6ATyfcwK+W8OAarYTJMSP2XICeISpE8EqW7vlzez/H6\npWImiXMbpasRzy4qAIwWWgVkPpFUe+VyA4URuNOW6/J+JhnKhv9550b62KM7CylPdg1PxAs/g4Vi\nJoWf4u1XFWTtsEwaOj1ORy5O5+/oSJH4R50YM6nZlkndEPfTlc6VLhzRurlFHSO3TPJZWpmkazQu\nj9nU6CTFgDabm8NJIqp+4OZixFcsLJ4yL3fc0jLJyUKqpBdzulqngBU3KbfLouNWtt4yKS3oqYqI\n0F0q3sGaQcOzzGvXqozAlR3xqn+G1UlyDi4UuQymgvJMEKD4+5q3QPfH922hd961UftbxTqbWzR4\nBy9qQocAACAASURBVKzwIBEwMf1xdB/i8mXefNMq+unPLNOWo0vTnOVSIa6YqrGV8hAvNeu6nxwa\npmUZrqP8unVmy0mAyfRvutXePHcC3mcPDpbj5mbT3+tgjNHFyfmGg/0y5e9YuIwu79LVUJkkph5f\nIFx7Vp8lvoem/Z7bdY7e9NnlNBYJxFygHrNcNOA0IvB9NXL95FaQarw2HWIfqma/MR8T4qZM0sVM\nyq9fEVz6TdOuNT+ggxfyFYy82Q8MeHG/u3DQTnn13K5ztOrASP6OJZKyCNKQlbGsLHxDPVoZgNvG\nco//orbVaSX2z9hMlUau6t3Z3nf/1kaqKRG7uTnOi69dmCiT4utucG79/O7zND5bo8e3ZVuhBozF\nixZZVr+ioiO2TNLNG0Slj3iegG9LZD67mElpeUuWp4KoftEYnBGAO1MxKcjU4pgtnjeOcaStp1pe\n+mRpyyRe53Q2N91+JutuGy5Nhe2/yBj2x/e9So+8epqIEmWdy/l17UR123axpO10xDZnG26ok7O5\nAXt6RpnkaV50nZtbVZng6DoYNzee/O2JFYa46uTWWP2AUc1nxWImWayAJsoku0nG+Gw1Npe2rUej\nTM6a47PoUO+xMZubxp85XZa+fHWz56X3ZSxpi7yzFYUJl8w9g6JlErG47ul2LR+nKvRUZZJWqWrR\ntomyLYOk+D+iCaygYDXB68aFARXXbG6MiguqjLFYYNY937xjOToLm7SbW/K3JMg6Ch22Abg/+dQe\n+stv7TD+zu+z7vxZlkk6gTlvRTbOeugQ/8EF+76D6K03r6Y/e2BbQyeSJhgsbaLPYzh9n2CZJK4w\nVzKUWeJYZ1p1/fhju2iqUqdzkQUiv7+2FqicRgQ+Nf6FSYkqoluJzg3AXUA45++1bjxutpubzb7q\nIV9afph+444NiWIu5/gFA1783i6wVCbdu/4EPRxNoFqFjSKQ34tmWiaZlFr5MZPKr0NWkekxKNww\nW5Utk37+8yvp3XfLweGbYRGnLrTYcm3s5uanMnfpmJit5ir4s8YkET8gumZBOAXKcjsTLYL5mJb3\nvHVuusygtDHB9zB1e7wuvH4ubm6mOEfiGF+TFEvhp25BST2L7rRqXRLLpFDhrY5f6qK7JEcWVL64\nzkOCgNFs1Y/7m8RgwSUmn6YeyjiYNcZ3G3Vpwdiun+lMy6R216D76Bllku5F539z018/z82twIqk\nSSkkDqpxzKQGLJOqsWVLcuChi1fpfIZZuCnLgw7esU1aWiatPTxK/+Wf7bIAuMd6CQc17hbB4fGc\nbJ+Pup9p9V4Urlxc8nR7hm5u6V/4gM+fCW+HiwYHtKa8JuQA3OnyOXlubtxHPVEmpc9lEtpVgTHr\n+Z4Ugp2LdfQEBauJPKHR1Ww5YGVZJqXLNTE5W6OHNicTM/k5RIKlIpyIe9QMwp0NqiKjKPxQfXw5\ncx+jE/ryFGL891TMJMkyyX1SHh9reR/4cZtP2GUkUTFZ+sUuXtFt4DFOxPdavPYsyyRxwmuKORHv\n6/vSMeMzbmm3G1GsiNlMicRJkqUyid+zvAl9VLKLO2gs0GuOKVueTLm5ZcVMij/lg3ZGbpIXcxZy\n+Ls6OODFfy+wdHObq9ZbHhQ1VuJk9A+xMqmZlkmB3B7EoNBZNCUAd0aZqkUo39MmcH+RBEV51zdv\nETPpynSFFl+3hDYJ8eGuXTgQH58li3D+8+dW0u/c80pmXXjbzYsVGjBG10TKrKyxVfwtdnPT9A7S\nNk3/FZ4zKsfFMskQ+zBe5Anyx8x8xVrUdxoWKLL76vwxNqVMiiumt0xSlelimUVjfbkuJKpZe/kY\n7RQzSdSaKdsCiz6vmTQjUZkcNsb9mE6hE62lOp2eUSbxQVVnmRTHTGIsPenWWWQ4nNeYzU04Da9b\nwJKyXV+gqqKMICJ6x+0b6L/essZ4TBKYzz5mkmiZ9MjmU3T7qiNO9dSWLXS+l6cr9Mbrl8WxQ0x8\n4ond9LM3yqlhed1s75y6n42bm4tLXrjSJG/TWiaRrJhhjMUD4qIFA07tTRQYGCUddp47jzrA8xgH\nXBDRtcd3371Jm7oyCEKLikc2n9KeS+S3BRc1cRDm9c4SUnXBREUqcQYZW+1iWTGTuIQjfWh5frec\nVUS8z/FqYIabW0PZ3Ch9rkbQCXFZxeqEpDzBKcnmJg9NjcRMEjG1lSV7LtC6w5fi70UU4NJ5NdYF\nD2w8RTNRm/YVYVlUnIpWWVkKU0mZlBOMnr8r/P7aWqByGhH4eJdVUSz7shfOkx9tYyYVsUzi47RO\nce0qUObdI7d4fPp9F0V+znkTqkAY+3kfr8YhMzFbdYvNWAbxs7Nxc2tFzKTU5Db7uHKzHcqfLsfo\nYiaplDWHvOH5JLOXyWpXZFck892/8WS87doFSQDuRNmcfeF5bp78WeXJvX7AEsukTGVS2s1N1x6k\nxRtx7OVKCXLrA05cnqH5mm90V09iJnHFokzWmKneY76vuNgjysuqe3YWunuTGk8FZajneSnZXLVi\nNVm4c2ardVp83RJ66JVTxnq5vqOqSyMfl136xkSXlA7AzS8jbyGomyjSD3ai4qZVVWrlMPs792yi\nDz1U0NLegt5RJmmybvCOcSpWJmUHKk4sk+yfsNnNLfmBz4sYo7iVur5AfFLh5ObGuECZvy+/ZjFm\n0mee20+3r2o8A4xoefHqiSs0W/Xpay+nU6iLvLD7vFQvojCwsQvqPa5aWLI4CXCUdlvxKD2hY0xe\nMfQDFg+ICwcTSyYbiws1AHeczS3HEqmImxsR0QVN8OuAMfrII9vpM8/tp+Gx2ZSg8NArp2jF/oup\n48R3L7ZMyrjkvBVoWzc3cfLaSDY3NWMNLymrv1DvjfguxBY/iiBrWoWzTYurlk9UzuqPTojLmvjo\nMsPkrerx39VVVv6MxffFBoMMm+Kjj+6gDwgubY0KePEEQjjhbauOxBMA9XdRmTFga5kkCf527wp/\nB22zdnKymt58zadHXj1tfLf4u85dcGzS3geatmurrHHJjhPE91/om6JPV2uTPGWvS3GB4b3irmp5\nfYGYzY33IQtMAfcU5mp+qcoRG/jZXJVJx0en6XiOy18ed605Sn/yjVelc8TuTPzckeLh79/xHwx1\na6gKEvE5LSyT1O8zlXwZR5dZyrZOIvvPJ2mtbQJwxwoJYRuXjeeqfjJWNngvk3Ts2YJvwBgtsnBz\nq2oWdPJeD51lpW7xMYtblx2mL684rCip0vXidVKv19byU6yjOD6LY0RsgawrS/muO29qcTP6DLO5\npd971SJJbFc6xR+ft3xtvXle4SoDxTFCo+9FYiYlbVHcJu9ju/gxMVulp7eftT53O3CxhtMdY0sQ\nuGf1cypf89waZXKuFs9rOa4yfSPsPDNBqw5eyt+xID2jTBJf9Hj1LuADbJLNraJacGhdN+zPa9pX\n3p6Y+fPNri9QyirCAnF1Mg9eH9dYGjaIguk10UqU7WRNvE+T3DLJ8h6ou4mTDClNvdTR68vWbmXp\n7Z6XzubGiEkrhgEjScAPWJi1zAZxji0OsOpgrE4G1PbGJ0/1nImaTrhnjOjKdDU+zlcG988+v58+\n/Mj2dFnCuxcH4M6yTKqF92yRYRI0bxmAO5FR3WKOSTBBYHYoI8vdkD8/1fVLHF9kQdat8qYVzaK4\nxpfTxkzKmejHlkmpANzh5+CA5zTXUPsK2+ffaNrcPIFTdfkSFadic8/qJ2uaVWS1p+fvDn9XqgUt\nk7Ke811rjtFnvruPnlOs8IbHZmnz8Svxiu6coozNtEwSzmcTY0kst1oP6NmdZ636VH6MztrFta+w\nfeZ2JBNQkYXR86zmpPAW3dx4v2FrmTRX9SW5qOYHTbdUslEE6t6Vzz63n65/bl9D5z55eZaOjIQK\nKX7dOrebwQHPGG9IHQMbgumfvWaX5Hv0aePmJlI0/gyR/KwSK2Hz/jolj/j+WWdtzCGZ/GfvJ1om\nZbu5JdeZ6eYmjbfyefgxrhPg85Pz0v0Qj+f14rKker0u7mCxZZIgfFyYTEJoZPfV2d/DuuiVRV70\nf1OA7nisEA7XXVdsNZSpQHO797zOvE/gzdYldqXulGo2U9vFj5f2XaS/fXI3XbKMVdsOxGeTp8zl\nuL7vE7NV+olPL6VvbjrldJwLWVV6YNNJ2lIg/MELu8/TX31nZ5wMhai5mfx2D0/QzjPjTStfpWeU\nSbzd+gETVu+4MolPOllqtVwnABYJlJm1XRczqagyyWXFsB53gjYBuMNP1xVrG8RrjX3kNZO1DUdH\nU8os8fk4r6ZH9+rn/v3305/98mJFmZTsJ94dJxNWSnc6YjY38bdpSZkkuLlFk4M/vm+LlZJi0BQz\nKUdJaszm5vOBTX8+nXAaKkWTAdZWu64Lzpd1u7mbmykLka2CNfFRL26hEzDBTUcRJLNMq9OWSeIk\nWb+PaRXONVZAWUGrObqJBy9W1w/q9t947DLdudps7Wi6Rj921RloSJlnG2/JVsDbePQyrT8ymtqe\nN4aoEydRmSEF4M5QaomnSNqmDF9559fDhRfXvjRr3Lk6H5alxtt7261r6Y/uezW2PuDvsypMc85c\nmY3TeesmY7avbtUP6BOP76Y/vm8LEYVuMW+7dU2c4lmEtwedm5vrO5M3yXDpekzn5n3hXC1bacDf\nl0o9oG9uOklEdgG4q/WA6gGTnvcb/vEl+p//qs+oWRaxIjAzZlL6WU3O1Whq3k2BkiqXWCozaDpm\nUvhemkSpMuOeJH1q/j7x92iDGoA7D1srC117FCdCScykrMl8+Kmz0pADcAu/FxiveR3s3NzCxc0z\nV2aMLoI66+B8yyT92GtzOaJS6Kde/zrpWYt/87lMzRQzycEyid9n8VpFq3Relt1cQjenUs+flKdT\n+qkLDpLrf4a8qb6GUvITxw49UQKGFMrmptmmBpq3VSjw/fLCPxShLCufYpZJbufg2Sm/s/VM5n51\nP6BzGTGFs8iyTLrxhQP0B19/1blMvghS84NCLvmu3PLSIbrlpUNNK1+lK5VJumYvvugL47gCkZtb\nJGz4LB2AW+748l1vVEYNmaZkZVISJFGX6tKG2M3Noe25DMSu2dxcEAcok2XSdKVO77t/K33ooSH5\nWFGZNOcWgJs/67f/9I/QD7/uGuk3qQjNSpkNjKUnp56mDMay3dxcUAUk/k2dyNi6ufH7a2orOgEr\nEJSiHnnWChrp3eMK1oz9eedrcs+oOFoKMdZIAG6WskziA/COM+b4X5mWSdHx6ZhJyd+NxUwSy2xc\nWNDGTIo2zdV8uvGF/VI71w2U//TdffSVleY4bCY3Al7UgkHPMQC3WmG742wtk/70/i30/m+mU2zn\nxrRRrA9EZZIYLyrTUkM4hXiv95+fpLPjYayzRJmUCDJEBSyTMt5xXl+TkM37LC4EmxSQv/LFtfTf\nvrSOpJ3IPWaSuts9647T8NgcvXxUp/QLP8uImZRnOaiWlzUxM91ufq/VFPBHRqZo8XVLaO/Z0PWI\nV0VUoNlYJvE+V+238uLUiDDGnJX2fO9sN7fwU5xMzdX8hgJyD4/N0rM7z6UW69S+yw9YnMZcR5kr\nzEkzMd/DIBmAoz3D7zMW90Jsdq4ZQkUqGmVS9mPnSh5hi6Ag1AXabyQGS15rD1himfTQ5tP0+1/b\nrN1P7+amGQvFQNnCdimbm2soA5L7XqaxWo7d3JQrdpkrqO1+cMCjCxOJMimr/z90Ue4btJZJGZXR\ndYNq/CyxTN3YakrSIH7N6pNWHRhJjQE1Zdzhyjq3mEnptpjUNfxuK2vw8VW3EN8o/Ln/9WM7G1JA\nFHlfXceK2Ksh57jPv3iAfvkW/SJSHs0wxOXPWbxel2QhrkxX6g3H/nShK5VJuv5Y7JD4BF0NwM1Y\ndsykjOK1zNd8etBglSAWK8ZzKmqZFMfaKGCZZKN15uU22zIpDsaqvER8Re3UlRlpuyjsJAG4k/Ke\n3XmWXjWYHCbxVwZSrlI2FmV5MI2fW+jmpgxoFLZB3i5Fy6SFQr1szmxabVMnMrlubkpAd9MgMKNZ\n6QyYMkhb3jPZzY0rbs3H2lom8We28sBIvBKhCz7JmPx8XZWt8wbrjyxUwUf8zqui9kk6U3bdfnno\nXIUaISub20OvnKYHNp2ir647Fv9WxIWiFlvK6dvzoOBGuv30GK0+OJJZXtrNLX0NV6bTCwLzDcZM\nynsn+K2JlRmGSWC2209yDi4IT8zW6Lfu3Eh/8XDoZpq4uUUTj2g1e1wTDyOLrFdFtQQ2MZeKmWTe\nVxeAO9fNzfBm8nugu5famElK9jlbsuq3fP9FWrLngrQta7IbxwpR6sDHi1lFyb86ioXw7M7Q1ZD3\nbVyZmFc/DnctbsSt7e+f2kM/+emlbgdZrNLzaxIVr3NC6m5bLk9X4r7pd7/6CjEWto3Qclx/3YyF\nbm6m8dclTlceyYJjxj5M/91GqSVegu3KuO7dElOaz8fnzVKAhZ9q3EeiKAC3RmlcpB3ywwdylKd+\nwKT3Y/95vcJUnPCpcXTy6kCkz+aWhXx/VFky+R4H4I76dLVpusRjSQJwh58LBrzY4nTBQDLm6u7o\n++6XF1O0lkmqxRAl5elcRxOLpHSZuusKDGMEk/ZJ152I6NzEHH3o4SFarsT5rCsLW7Gbm5MyST6W\nKLkm/mxt+w5ubdqMbJa8XR+6OOW0cKAiZ3Pz6G8e30U/8aklRBQqU3Qyt7thhd1c+PkoPlER659m\nxGPi7+tj24ZjwwjX0BUin31uH/3mHRuMv89W66XI/bZ0pzJJg9gdeZ4XpcQNH96MIMSqDSucGMud\nMf8+NV+juapv1Gxmx/0RFSiiZVJIUTc3XeNYti8d7JhIn1HIBK9PMyyTxMGUvzzqKgB/0VSlj9hx\nczcK8RZ84vHd9IcGk0M+GCwY8OiahXbKJNNz0a5EpXVJkZtb8jdReG01n9H3XbswPHeQTLQlZZLF\ng5Ld3Fhyjoy4O7r6V5WVWNN161wIVNNhW/crnRY+65q5glE13+aIcRr8gNFfPDxEfxCtLspZ0/h7\nIK+Yu2bus0l/rOIrD0IXM2lqvk6/decGIUBxsn9NMrF36zPEepaxQKFbxebFVjQTOl0Abo6pvZks\nk4KA0YAnv1+/+9XN9EHFklFFPY36fWK2qs2I2ejkMAmwrf/dD5gURFKcEIvtUndfOWLZan0vRwoy\nk2USt1wismsbWeMVt3gxWTnw9y+2TGL5ZUpubhbKp6zf+T0wxX8j0lsmuQYCzlKe3rP2mPE3HUz5\n5PDhQrUY5c9AXf2sS/1d/nlNlkkuPFkgSCw/XVaSDF4j8VnN1Xwnxa8fMHrzTavok0/uJiKiS4Jl\nec1nxglnnptbozHWRJLFD5fxyX5fcfJeNM06kRzU38/p74j0riN8DBSDvotjXpHJEG9LeW42Pgut\nnvMM9mwDcIvbpIUcYVHX5noky7FAPkY8XLVMMiWt0GHM5iZkfhQtQl0CEuvOqyqARCWL7v7HSgfN\nHEbXZk0W9jZublwxr46hseJQsUxyipmk2aa6c9ork8LPRhe6dPCxMVSsF+/L6tKCMdEzO8/F1/kf\n/mkZXffMntQxzQr5cnU+MSIhIjp2aZruthyHiwx/B85fzeyHeb3vXH2Utp4cI6LG3Nwe2nyaDmQo\n/uaqvtV1PDE0TJ9/8UDhenC6UpmkWyURtfkehZ0h72Cm55PVNp0mMKXNjr6+6YYV9GtfWku/cuva\n3HqopWotk5ggSDsOkollUrrOpkCjupUeE1nB4G5becRoxXFuYo4e3XIm8yUS68pfHtVUM1YmLZCb\npHisq5ubaLKrKqnEMsSxzKUT0e0qurnxT97+vu81kTKJsbhtLlzg9goOpGImcSs8RWmRY5mkbjc9\nP72bm3i8fXBW/u5dna/Rrsg1LKtt8knDoEGCmY8zHLI4qB2fREsWSIwLGvZmzyoBY6kYTXlHv+P2\nl1PuKLpsbkThqujm41ek8omUtMTC39yt5YBhNTWsnyiE2l3r++7fQu+6e5P2OK0VJ7coiBW3SXvO\nim1gWkFPUi8r7TeyDCBKB7jPQn0P1GNHpyraPo8LVCbhedm+i/Tee18xntcmGPPPXL+MvvbyCSKS\nlUliX5slaIr3SFU6fe+1C4hIUCZFAihPQCEqiV3GBx2xMslwzVz4VYVgU5l3rDqqbXd5Y6bp12sy\nlEmJZVKTA3BrGlJW8aZL5X2oGjfjStT/cTdTXapvG0tMNa5Vq1D7EZU//Ppm+uq6MFNTzWc0OVuj\nmh/QXNXXKwIN8P70RcVKjCh859U2xq3UfMYylQ7NcHPLelxxUGDlGBtkNze7A3XWI/yaxftvY00l\nlsW3hQG4eZ2Se1nMMonfG7nOt608QouvWyLtN+jlZzkU3+uapVWE+KvYpmzGYVEp5AveDOp5a4oy\nSbWay5qnqtXg91nMpprEtnNfeFMRF+2JRMskT+vuq8bJy7NMMo0RsqyqvwZT7E1TzKQibm5SufHi\nSPi55+yEVeIjvjDZDDe3JHsla2ghTTfvJUr6qyeG0gsNrnPhOL5dTjXVNvG++7fQF5cfTsV21GHq\nQ0xsPn6FfvPODZnxU3X3tZEECHnM1nyr/ubvn9pD92882fD5ulKZpEPskDwvUiZFHeO06OameaCp\nCYcwFIxcrdCUKTCf5EqjdGKKuR/fJzZhdmxDqmWS2AjHDS9HXemQs8iqzx2rj9LZcX0gs6+vP06f\nfnYvvaARzuJ6CAILv/+qVRcXIlVlknidrpnmarErWdoyiRk6PdfVQHV3z0vHdOGWca+7JpzghdY8\n3BJL7Kzyzy1nc0tQ27U6cch3u3FRJiUWFX5gbzHDn+UHvrmVblt1JC7LXCd+vmSb+HziNsQSJdIP\nvVaOjRUeE+8m+ys7dOQBEyyTLI85dHGKRhUXKtliSt6fK4Zky6SkjlXhPVoRmWQv3Wt+74pYJm04\nepl2DycxoCRBWqdMUuopxmXJMuE1Tb5MWapCyyRuGWD/jqYC0SvtzdS38/5Wp8hkjNGGo6O07ZQ5\nU4Ya80HFD2ShTXTzENsId7/RIW5VJ+ELI6Uerz8XQLXjn0XjyFQmRZMxUzlJJjlZCDad9rZVRySL\nEWs3N0MdY8skzfseK5MEAd1TfrPFNf5MdrBiPuGQt6sWpZyRKMMPlwV8jZxgI7RzpWYZsRbU53XP\numP07E691RLf09QvHLo4RScuT8fff/ZzK+jDDw+FMZMclElqFkWRzHeN8f6nFW5u8mfWPhyXxyVe\nQZbCXz5f+gSVWJkkLpBktGl+fkMAbj5ZlpJUFLityeRf3n6HkvjBj8aUhXnucBrr4LzbLVspJZ82\nXYoUX0e1TBJ+4315kmhHqbfDzePniK35BweU55Cof/IwXaIuXiR5+gUbXxk/5QU2jYLGMEboFhVV\n+Lig/sz7Tn5ckQDcsZWccN9EJR0R0fDYHL3nHvPCFCe2TCrJzU28H6Kxgm2mbR2mxdLMRTHlfl6a\nys5Wl8QutXsOvPzYktLivXAd/obHQkvvfRmLu7p7YLMIMV2p05NDw86ud7NVH25ueejujzgeeOTR\ngsEBOj46TYuvWxILpqFlkkagDPhx0XfL+1+XzHGVMoXvSTY3intad9M+ro3VKJMMbniiea3uN9H3\nNk/QVCcCnGsXJtkwTOgm8OqLxTswHqBbzM7HmeSWSZaTycT8d4AWDQ5Kvxnd3FyUSZq66AJw83rw\nFfIgSNwtF+asiqmIk1vxPKmYSeqgmqfFN1y2allDFCmTor/rTpZJYSXEgNVZt5ufxTxAJavoXJn0\nA69dmNqP/xkwOUuRi4m/FDPJMNHToVqMiBlS1PdyJBpEA8ZiSzrJzS1jsvrE0DA98upppc5y/Ysg\nvqe686tZYAYF5WhWcMGK0p8s23eRdg1PmC2TAp6a220VXt1XvefThkxQvD/SxUj52ssn6NtbzJlE\n/IDR9c/t156fo3seJvNtk7WGuJtq9bNAiM9GlFyPdvyzuKFZ7zhfSTcpD/k4owpOWcKRuK947rGM\nYJqm0vi7pLVMCngdi90XkSzlqW4Klu2Gwj/lfUxJBy5G/UpVcXMT62QVM6kqyxlZTM7V6G8e3xWP\nyypqW7t12WH6xOO7tfvy05mE6/maL03qiYjWHg4DqpvkOh1ZlriVunksC4LIzc1QbhHLJF2mVLFu\nWe+H6nbkkpRAVIg14uZW9UMFuGiZxCh0oX3f/VtS7UKXZU3MpphYJglt1vEdFIO/m+JbJQthjAYG\nPKMb/aDG4jLuizXVkmWO9A6M7OYWYr39QC5JPEcqALeLZZLyXXWLHRzwpD7ApLDS4SJbewZlkuoK\nJt63k5dn6MMPD0mZC01JGsT3eWq+Tl9ZcTj1rqpeH5wk5mz4fUAzJ8lDt6fOY+TEZfP8iVO2ZZJ4\nGZV6QNtOjVG1HjTkeuVr2gyRwY1cc8xT28/SW76wWlrQVOGyjm3fwOuRuILbKJMc+0Vxjm9A5z5o\nM26tOjBCn3xqD+3MuCcqfsCoWg8KKeOL0pXKJB1ih+R5oTXK9tPyyrEuZhKR2Z83D/G4dBaB5Dt3\nTfKFSbjuRRidqtDFyXnyA5ZK8ap2eKKQaIpzJMaauDpfozWHkmC1n19ygH7m+mWZ2Snk8xsGCAvr\nJ/Faq7EySX6x+AvOV5H54xT9lic0MZOyEK0lrlEsnsQi5FUDfVnazSxdl9AySYYPHskELxGYREss\nm+uS3NzIHDMp5eaWU7hLNjdxhS0I7AdX3WRLd+Thi1OSv694nLh/RXgnrkyH78APfM+iaD/hGOE9\nMLmQ5cGYu2WSWEfOX31nZ1Kmsq8YdyJJIiAoc0RrxzgOW7jtuV3n6PFtsoKjjADcojJMG4A7+qwK\n7xon6/6qAt1ffms7vfvuTcaYFHWuTPLclElpq1MZ04SO908DmhEyL+i3Lmi9iu55zNX0E3nehup+\nQH/5yPZY0JKs9JT+lFsLMaUMGzdv2/pyeFs1rYTze6w+86zTiv2ZeO6s4KC5lknamEnJZJYomcNg\naAAAIABJREFUdNvmLmOub4xrxiJ+iX7A6MjIFM1W67FS3HS7TbETuSJaTdRhUsqZ4EHSbQT1b716\nmp7ZeY7ui1w1VYq4g1Q0fQaLFPlZdbK1TlJdV0QqtXSMiVjxwJKYbTpc44wcOH+V/tNnl9MLUZBY\nHZkLLal62p9bskyK7vfLR0bjgMtE4fWIMqip/KofSNceMEYbjl6mDUcv04nRaWlfXdwdcYyPrWMC\ntzYrn0N/HhFR8TDomZVJOuUBjwOYN57qqs2Y3Tgsx0ySreV0Fjqxa5pqmZSlrFZ+SpTPiUWupBhw\nXHjToUuKEjqup++/qsgRx8RPP7uXVhwYoVeOJYl3Eo8NRt/ecjpVDlEYq+bONcfoiaFh6Vym5EaJ\nZVIYr5Ur+dzkRnObdxXJ4mxuJcVMEq/32KUpeu+9m+nM2GxmX5aVpIBIsbwXlUkZZYrtlIdsOXpp\n2rS7ZebIdJ0WxslI8vtq12czoMjjOnTyh00Abi4/mRRsuucRy5IZF/Khh7bRzUsP5p7flq5UJulu\nj9ghhTGTBuh7FqWtUbJWJ/kL/y/LDtGqA9kTBiJ955icS6xbcn7+4PmLNlOp03e2hjGHfvELq+it\nN6+m657eQ2+8frlUnipESlnODKu1ieDE6GOP7qQ/f3AoNiF8MvJd5S9W3qBt0lbzDi7reHGSwe+/\nOsnm9eCryKp/spjm0PY9F/2/Vfc500vm5Oam6TrCya5ekcM7M58xIdBhOZZJKin3npzna7of+mxu\nyZUXsUwSUe/VfM2n//f2l+mjj+6IL1Bs6+cnEndL8Z3gk7AffG2kTBKK5X+Gq5aUOt6ElJKXiTGT\nMg+TyBuYRbjAxojFsbTEa88SYoKAaFaxIpMskwrKH7Jlkk5Clus2KLTnqh+Yg6cb7r0pm1vAuGVS\n2o00C105IkbLpLrZMinv+YsWWaZ9dY9SF4CdKLEqujRVoWX7L9L20+N0bmKO7l2fTOLVcW2RYpnE\nf6/Wg5T7h03byHrF+TM3mf/HyqRU8gtzoaKpvejGbVL+EZnvdZabGz+EC7ubjibxB7PGgvtePkE3\nRUErdRYMRCTFIdC9BdPR5P2OVUfo/7ntZfr/vr2D/uS+LUSU4ZIRPceHN5+mk8Jq9gi3TPK54lGe\nHBLlj/EPbDpJu89OhufXtIkgYPTcrnOpZBlq/CZOEasXnXzGrylrDmfr+pEVKLpSD4z3PWChFYvR\nMskP6PZVR6RnksWRkSkiCjOQqsQT6CxlgLKvE0qA5+lKnd7/wFZ6SohnctOLB+nPH9yWW1SlHsiT\nW0bxPTClafd0G0lvTVckoyI/ZOOxy/S++7ekZJ96wOhTz+yhIyPT0QKF/qny7aJyi/+tq5ZNjEL3\nmEl6WUZbtvLdxc2Ny6j8nfU8RYkWlWUTQcZ0Wl3yEc/z9AG44wXAtMzP74c4vxP73qeEBAA6zwZV\njkqCTzPt9pOXp+nnPr+C9p2fTJWZh+5xm6yo8uDPqGg2t1RmQI1ikijbze3HP7WUPvLIdu1vQcDk\nGFVC+fOxpXf6uBlBbk3kLmMV4rJsszHz+8wX8+drPo3NVGlqXrac3HlmnB7cFI7ZOiVgFjax6/Sx\nOfPfUT433mVQJunkLi5LZtXn5OUZOnhxKvf8tnSlMkmHOCfn2dy4CxYnYPoJmU6Dv/2MOR4GJ2vQ\nE7/HqYaFgY6f8wtLD9KnntlLrxxPtOw8G4ooWHELAX68KBiLwvbSvRfo+uf2hefgnVZAtPds2BCv\nztWp5gfxarJo3ZGFMcaJ4lesQxQqTf7JKcuk6O3kg/eEGBfKsg+OLZMGNZZJwuXIqwZuHbzaQevc\ncPij4lYbQZBkjREtOWxOLbZzRubBPR2IMLtw0yqWbvIWMFngtU1Bq49ZIn/nHeOWE1eSeDzCTm+L\nguHXlQwyPDbRa6O4VGKxYpwMNRh8ltuMmtK3olgm2Sg1stwfTKuDQSC45ojxxrTKOF4/plH8FRfK\nOZIySZeSV1gRJEqsVHh91feOY7ov/BqPj85ISnI/CFeRTZZJYQyitJClvp9zVVn5mRczSatM0h6R\nPjYLnUAaK/aVOvPr4sJwwBh98MFt9PSOs8Kx8jljJbUy3lT9gH74dXJcsUbd3HgfZtpnVnBzEwXA\nrPOKbf2YsEp58vJMbGHLGJMVvoayMt3cojrw+ye2h6xu7QtLD9I3ImURV/CrypPbo7hwRGkXFCKi\nG144QBOz1dh8fdfwRMoqSr1FYh/6wYfCyf7UfI1mFFfCxMrDvg+48YUDcZBr3bu+/ugoffyxXbQp\nWj2+NprMmayCbOPxiHXTPaPYrSGjPFfLJB06ZZL4HLJiJl2cnKfbVx2lP7lPn1lWhcumulXyJE6M\n+XjV1bpo/173A6rWA2IsSXBCFFroiXHLTKVX6n4qADe3SFLfB37rZTc3oS5xzKRGLJNY/D6tOzxK\nG45eTllF+AGj72wNrVMGBvTKDKLkvdYlkHFZ0OAwSsfY1CG2MT8IJBkp63j1XmUb0Kj7RuO4oCwT\nxyG3LMf6fY2WSRkBuPkRuvYtKrHFssWxUBdiY4HywJPg0zL8WV+6WqH/n7w3D7ekqs7G36o659yx\nb8/dDA000NACAqKIEZEoDqBGjUk0amLikGjilC9q/IhTjENCNA4hokETNSpqnFFB5hlBhmbopmno\ngabn4Xbf7tt3OkPV/v7YtfZee9faVXU7eX55eH7refrpe07Vqdq1aw9reNe7MgXDG1uXM+mmdbtx\nxwa9VjoOQaUwNtkJOuFDQmm+h5vmVgZ44FKlv1wXAFoUbA52A3KAScHzP/+Wrch7Vc69W+bEmW2G\nAK1D9N5nuhme+cnrC4W1vvubLfjcdcTlWvPiuRh1q2SCSntbHYdvlTNJel/U32XrlFLAeCBF/XDk\nqelMEvrHjxk1k2LVn0zJ1dwkxSlE9hyqbuTfi3+0/D/2e/rtnnG9YUtGO/dA2+hcriSy59DlcfW5\n16zZhSsf3GHup9uijLL1/h8+hLd8494C5K9KGQkZf+TFLltg+SIT4lGhdjyyYxy9NLNRofw5ef59\n2QThCxjdqxHHBWSSgjZE/vI79+M+lg45m3RhpYpDUTJ2acEgPqheZp/AdQ5Vr2C+cVsF5Q599mU2\naW4OZ1Kqait8dfhaXEg33UMwMDj6AwqjhzrO76VyurzELaCVzWd+8vpg2lLqGWK8epz+X/yZI9JC\nrwK/J6dZppSZn/zZyyL9SrkRHvqOt/9whDtopPvbcUDIJO5MUoV5RxKs5sbu8ZIv3Gb+5sgA6Une\n8s17sfIj15jPD2wZc3g4SH68ahu+ytJypPENWMehqcSZKSy/+CpceuP6yr6s40ya7krrvRxxo+sd\nZNUsfSWgmOZGsGstvTTDZ69dh50Hp00qKEmdlKayKGAVZ5JtY4av3W77vm4UbyNzJl3yq3V46ze1\n8vmVWzfihA9d7RTY8CXNbCqw9F7osWj/4Ui1di/Dzx/aURkBDZaMrjHlNu+bMnvdZLtn9opQxUg+\nb+hvIt/m39F+PNs0N3tu8TtCbX39jieglMJA7hDxeeGq7rf9QLGYhwmSSdHbGujpuqkfZXqKyDGR\nn67JmsP7LY39/QG9UQcS7b0HShxxtZBJippX7Xgq/tj+2U1tMRA+9qc7aa3If7vrIpMUlOF/CQW0\nuPOA34P4GR3OpFladRv2TBTSQfx3zj/rZbI8zY2f3zPIWf350EzXKatOIiKXVD2dgfs6tK7o6iEh\nKfJkVo8fe25+P4aOlp67SPJdvEfoti4yCeZ6Uu/bwFp4fHObyXUmyU4mU/XOcyaZgLg/TvJn9sdP\n3TFJ+xTg6vapUnjFpbfXuoZzXy/wMVspAB7Yc7hFPw7PWeX3i8OZVEIbIEmI74xfK4R694We27d5\nx6a6+OadT2BPvn/uGp9hRavkdxyaU+R/KBsaUr/WQe/S+35y35SYhSTtmbYqa/i6mVKOHqmUwp7x\nmQI9UF15SjqTZHI7+10Uac6IQrn0rIqA2w7O0Yny1DGgnDPJQSax74whmrmLszR2p5jBQU6bibZG\nFvnPQbxJu8dnjHJAimmm7IBcu+MgVm8/yCaWjWQ2/aRrJiECbp8YXBL+bCGDgyb46EQbX7jhcdNn\nNLkJmSQ5Cd322H4h4zyJI+PIIcmUVuR+tWYX7n1iP/tevnhIOfCHYqaALTmzPwk9A1WU66Y2Dz4U\n6QyJs4CWdERVeo8vISea76DQt3URdmVVDbmIzgjvK8X+L3PacAMmy4B9k23zt39do3grtx/ovYeq\ncvnOJF49zj8eEinybNM13d93mVJKThg+z8siWQoameTyJLHjs9PJjXDIs+R0N0agF/0BypFJIYcL\nR16MTrgVvZIcGSA9y22P7zV/bz8wjdd8+df48E/X4EmhMMBmlooS5kxykUnUri/dtCHYl6MTbWz1\nOAdCDmJpXv3lFffj0Ey3MK7oHZAzKVWqMCd8hcKgIPPG3rFhFJfdvBG7x9s4ftGQcy4VY/Bh3845\nJePHpiSXK7mdXuY57ksMezYOJHJSpRS+fZfmxigrzNDuWR6cOpxJHN331z94EO/93gNOmyWhvvar\nHdaZcqOH2g4/YFUqt/QMu/OA1HELB221Nwo6cZRHqXOier+gKPvt60dx/drdpt1BZFJgU7mIOYnN\n/fP/JfSqRSaF2/8/g0xKg5V9q9Lc/LaS3P/kGFZ+5FdY+dFf4certpvv+/N1UUpZUd7/ktg0ILed\ndYSf2U0zM+a4Y33G64vQ0NFpbm7AYcs+rf/sPdTGvZv3QymFHQemrWOAp4Oxa1Ha52zQdLpt9hyJ\nDN7XO/gYKEMmxQLi0uf0O/3j1+Ht376v8Fup3f9y43o8MRrmgjH39ZxtfFkt640yY75KbJqbfT7J\n2eDPAJlHUb7vsz51g+G8s8ikSHTQ+lUX79wwWjinljOJB7INt5R7w1B2hnHMe2vS4ZRz59dOM2DH\nwWLFsg0lPEH6d+5eVSZv+cY9uNSrXug/H//Mn6msqmWd9pnP7BqUhixVx5WkzC6iNbbutahdPM2N\n5OO/WIt3XrEKgLadq1IQQ9/bQghhkfbuOnOU720Pbiuik8qdSWU2IhyevF6mcNG/3I7f/0p1ZUFJ\nnpLOJEl4n0WRVvCK1WNkZeX9P3ywsGCMeiW9SULVoMoQFvwcboQD1tHEDRAamFMCMmmi3cPb/vO+\nwnOMTepBsedQ2yya1DzfmXNwumuUTM6ZVObpDRFw00L87bufLJCGk/C+qUorAYBHd9o8Tnov5Cyb\n50XVfdnMjEeLTJI5k3jqB4n/3q5Zs7NAbHzpG87S5wr333uojbs27cPOg9M2wkjOJOYgoN/yHq+z\nfocg4r7csX6fg66r2v9mleaW2btnWTjC4YuYplW4tlWS6zoNOWeSeQ7HkWI3iNAGKonrJGMlSfOL\n13EmSetNiGS6za5Pjl2e5vbzh3bgukd2iffJ8v6a7qa4/NaN+Ov/erB2RJNEeh43zS2sOFpkEuNM\n6mWHgUySv08z60it4qEiA+3Hq7bh7UJ+Px/Thyo4k+w9KaoZnndnf+oGPP8zNzsOuJB/RUJEbRub\nxjfv3Fx4V1KaW7HKl3wjuhTfS/qaMd79whXmc6oUXvz5W3H6x68LPFm5I8Ly+JWPsU6aeSkxJc6k\nCnRXmlnHCzlzpMvNdG1qnZQe4COT+HigNlQ5KuIAMonvJaGdde9E2zGmDs30sPziq/DE3sn8Gu75\n7l6l/6dKbscuGCwgmLts3/aroXHxp7a0Fqxj/AqHZnpmHQsZN1RIZM32g873kg5AY+HWx/fi64xr\nCrDjv5SAO+Bo/4erH3UIeflzbfWCPu1u2IhSqjzNLSRfuWUj2r0M3VQ5EV+6joxMUs7/Ynv8/2dh\n+/Hrcs7DiY6PTKq+VqeXOfNqy/4pMy//6vsP4rX/dhe++evNOPeSm/BIXjb7J6u2Y1VOI8GHGc09\nPo/q7LG+7u+Lv89zByulTksilYK311IGYXdLXlWQtzT0Pn72YJhwncQl4HbX+joV/khKncfeZwoE\ndAwySeZM8mU2yCRApxLp6+f2T1Se5kbP9OU8/ZbLZMCZxOcUX/NCVduqCLirkEnbxqZEtCUXN7gp\ndxBP95LEEnCnIqCAy+rt4wXnVFmlOz/Lpg4xdKh95n7sM6Vh+zZmSN8rAx0ZpGrNRc/qCS6AguS+\nJ8dw3SO7sOvgjOVEy4/5zai6Z9n8lHS0KoqQLfumMNXpoT8HIjwucBxJ+rBJcytprkYm2TnUS1Up\n7UeVPCWdSVIH8YkSRxEaSeQoXvMGm0Fk0p0b9uGx3YecRTzoTHKQSdxY89ojRBN4G33Sb67E0ibG\nFSQ+EG97fG9BcR+b6kAphd3jM2bht8ikYodR9StbXr2cDDpEwE3tmuqkuDZg6PLb+zwoJL5C6hNw\nUz7//MFmqRNlI6sgQhM1kTiTFAxvkruoutf7i++swv/98WrnO7qWKhh19m8OGadXRegovlDPVjl1\nnElKroQBaEP6zd+wBJqHuwgG09zy03tZ5syDshQfkQC3ZIMra7HrTIJJc7MRLXluzob/oJDm1pWd\nQGUiVnDoycaC5R+TkUmALYdN4q8tk+0UD28/iNvXjzrPXSdIKW1KVWludF2Jj6CbZoavxpcQ0jGk\nxGhkgEYd/fLhndh5UFbepjppgRPBF27MBpFJ+XpEl+oYx3RcOQCqeKYAq1z5snVsqohMyq83ztLc\n/Pfpr5/W2FRO+wEN9+ZdlGaqUhkuR57mzqSKQdbxUAxl3UjtPWKkXzyeKsuXRI/ysn8ppg7sPdS2\nvEhCn9OxaYb89eXSG9cXHCJcQgTcdZaJnQemRUj/jabyqrdGCOvJrhymv2z+oBkrfnUmoLgH3Lt5\nPz7809Wae8pHJlW8y1TZyrhhZJLCe777AH7nX+8o7CMz3RQ/uHcrDk51cfanrsfdmzRK9MBUF5/I\nic3tudXIpJleis9f/zj++r8edL6/9pFduJWtmbwP/vYn7r6uOZPc65rgX1ae5hYSvsZv2W8DXXbc\n6b7bun8KZ3z8WmwenazlIDIxExMomUWb2N8cDeeneNYJQGjOJDvGNu4toisINcrJyW9/nLhkmM6U\nj5HZEnDzdyrNJSlDgYSKOkhiqrk5RTBsf9+3WY/ZExcPFZ4l1Ooq9Im+L+dMUp4jIvy72aS5FX9L\n/1sdx9GLA2luYoDJayTPeJDWL2m7lgLhvjjIJI6CcSrQ8nen//b1HClNEShSi9hrup/P+6eb8bxL\nbgo3FK6OGVrHKisEMmfS6R+/Fs/9xxuD5+qUaW88+M4yh1jePfboznHcsX4UupJmcX0fn+niwz9d\n7QAIyji7rnxQozJ9Z1JI/yrDgNYtGkViCLjjsAP//ifHMD7TQ6aKKclcQq/IVlcOi+hMKnHa7Zto\n44LP3YIrH9yBBTmIQspO4HNq6/4pfPBHDxmUeVWqNLfJiGD+cOUp6UySxIlOQCv91Mlvfd7xOHnp\nHM2ZFEDYXL16p5M/uK9GmpvrzVX4/HWPYfnFVwFwX6JVSLjineVt1YOQO5MIvscHjs9LIKW5TbR7\nmOqkZiOg9o0Jefx+mcmsEpnEjRG+Odh27Z+U0yR4X3BOAT6pN+51UxksAbf+7UGGTCrz/vLNmqfe\nFJ1JRQXab2tI6OkVwotLfzNx+FYAD5mU/87JWqu8M8Bt8ypoO1WM4W0ISWhhlpSFTLlOjDKnIBdp\n7mkEksK/374JoxNtoxRrsspwm51UIqVYmhs5atg9WKoCf79mDgVu46axMuK/WSjuknOk60U/SHiE\nTOJMAtz3z9tC/TbV6SHLFA5Od7yUt+pGS9F9jrIRI2HGmZTPtcRVhFteeql0XS6haFsvU46ze0fA\n+fH47kP4AiM+lmSCQXsnAqldlO40OtHBX//Xg2a8xVH1POVjMzSvQlxN2w9MCwTcuk8MMklQdnxF\nxYyL/Gs+j5tJ7FgFdcZzFVxa36M8ytbpZU56XzkySZ+3YsmwePyhrQfNWClzlD8xOsnmhuBM8lIH\npPdy/5NjeN3ldwXvYTmTZrEw5LJtbFpUm0Pzg+/DSil87bZN+PGqbRhqJRgZaBSqvnJl0d8DXvtv\nd+GK32zR6C2vD6V1P/IckNSWkEHQyzJTyMQfn5+//nF88McP4/LbNmJ0olOa/kPIl1JnUifFpTeu\nx08f2O5830uVi1Rg1/C5U9q9tHAPu74qjUyqVc/KCu/XJ/dNFb6n93zlg9sxPtPDD+/fahaYg9Pd\nEqMm3+fsN4fVJs15qNvAx/50x+8L+fp+mpvkTJoSyGCldZ504FBwL9QXWcU+589L/rmUgFtwEltU\nscJ9eXr8SUvmFH5bJ03oyge345X/ekfh+8N2JnnHZpXmlpFdQr9RbhaG57g339coqsL3bYO+duy1\n4guwelz4GSacYglcB5WRbRZJ6bY5FFQMIZO++5stODg1O+Ji/hih1xJB70P/ePWjeJtQSZHaMZ3z\nlJVRsUx308J+XECflnCTvfqyO/HH//EbXPvILjz7UzcUdMPfbNqPK36zBWu2jwevwdPef5kTayce\nYIEjY7iUIpPyvaRuumFZmhuJQ3qvFAN7uA0J7UHGJizVaSRkUokzabKDXqYw1Ukx0ErQasT4lxvX\n46IvumnifG99/w8fwg/u24bbcn7Dcr2tqA+QHE6a41PSmSQ9Jv8uiiI0k8gMtpecuhRJzrURGoCX\n3bzRgaCG+En4/PSNzUtv2uB8tm2zxqxix5WySCnOV0GbGPf6+qgO30gdm+w41Tf+9ab1ZiPeJeTn\nkvAKQmURfT4R5vQ3zd98IIdJy912ktDzHZzu4meeEmghxvr6u8ZnMNRK0NeIK5BJxTS3EGeSZISE\nJxFTQMgLrco81fZvegaq4KLfuXKuVVe4w0+p+pHSKi9+Xciovq81Znupy5lUlhISIuBev2cCn7rq\nUbz3ew+ITlhJuEJwYLpbTO107mGv5xC0Vxh/Bc6knqx0lIm0mIfT3Oz35Ezy20iKmf/e6X1MtHug\nQgNc2aqzOcwImx2f3zKkXTnPxPPYu6kyJep94euZpPAV7pMjA0j4+szf6cd//ogpQBCSiRrIJG74\n/fSB7diZr6FJHFU65vayddhXFr7wh2cCgFB5T8udG/YZLiASCiTYNLcwVJ+krI2tJCogk6qEUL2S\nE09Kc/ONjCjS73zPoRn2u/D9aHxwZxLfn153+V0YF4xPXzbvmzTtmyohO5YIuLmE0jV5u3zl3TGY\nAuv01rEp8Vg7FC13Cg/oqnKb9k6i1YjRl8R5ZS67JvvIpG6aFbixtNPCvY+0H5y5bJ49nllkksRT\nA+jxQPubPx5H8zlCwZ+t+8PIOFskJHhKcN9Jc2WcfybxlyaJK4Tra3FJSlRI+PK948B0AQUhUQPQ\nT9bvmcCNj+4Rr2tMfra31Sak9XRYg0zyOJPqIZNcZ9KmvUV+s0mhTLVUBZjuH+IiDTWHP48YvClD\nJpWkLtL3ImcSUOBSq3a9ufLYrkNYLSAefact74OySl4+Z10dNKk5N/9sqqipcODcvWdYJyBxK7y6\nx6IA2s+muYWewHVEhIxyCTUfQib5lyD7QXKYhbIwQlInsBdHET70k9W4/LZNuHFdcd77gY+Q0Joy\n083wnu89YHiqigGDMDKJZPO+KRxq9wr6Ctl6ZWNE2kP8YOh4IJhXzpk0O2QSnecTcHNxKUFkoAEQ\nfnc+h50kIgG3t7bwdnCAyUArMTx767xUNwnxZPbMEn9bWVsPJ83xKelMksRHJmmlP/8c6c+pUpVc\nDFXiTMCAZ5cb2/oL/V/mRRmmOqlZNMYFZ5KT5uZ504vIpK5T1eWLN6w3m8vOUmeSXUjLkUkpjprb\nj0XDfVix2Cr4vF0SAupH92/D1rEpdo59Tnq+H9631VEGlVKWgDvVfXndI7vxvBWL8uPBZjqVf6iP\nmkmgmptwoToLlF3nwm4F7miiV2WRSXYc8DWzjj/H50wqUx/5sboQ2jpy2MikiijW3kNtL81NbtNH\nfrbaec+ugaqc/wEXveMSMsoIIRJnLCjXqAk5Z/y0Lmk82Yow7jFraChzHb/PjHFGSh/ca011LOEw\nd9zWeb3Su3PS3ISL0DdSX6aZRVgB7vriEOWn1UqNz+nmGIisHx/aVg3V5Q6DEGeSn45wQ14ON4ll\nAvB35SSOAPC+HzzktJsLOQMvv3WT+W6w5Tq6/fXaRybtm2xXIpNIpHmv09zcSFyVZErhY1c+gnMv\nuamgABIawSGL98bSSH8Th2Z6TjS1bE2ifYVSSABgTn9DPLes+aOH2mauTJcY7nS/EKffESP9uPjH\nD+NjV64pHAtVs6tjjG8bmxYVZ8uf5n0vcCYBuuBIi+0v9MxdR0cB/vDyuwrcWAenu2KaW5Yph6Pt\n1KNG2LUsyjsUpe9lqrBe+bJrXNZNuAEXQmlxCVU46mVZ0JnkB3I6QpobCaXZztKX5BmRml+FrgfI\nQUulFF5x+pE4YdEQLrlmndh3dv237RtsyijQMjkw1TX70YSHTKLbfv+eLfjePVvF33d6mbP27Dw4\ng+E+d55OCcUGpNQiKc2tTtq7i7QqjgN/XvacMRB29ErV3Oha49NdrNs1Xjhu2lpj7lvHjXsuH5e8\n8i8QzpjQ1/M+s+senO461B1+63xkkoLb9yaTwussEbnufcd1gDbTcQAi4A5zJoUQyICr99VxdtFc\n89eKruDYBKzDU3rGfbPkluGXCO4LEXDPZlsMyLdVOWdSmRD6d/uBafzioR2meq3yxke3JPhDwomc\nJaJ7Z+7lY+RVZx4FoDgeSb555xNmfwuVpvfBBVzo/U1301r2vEEmxUVk0lnH6gAJT/PnnLa+hJwz\n3AkbEqmt3AH8nbufxAv/+RYzf/h63N9I0BdY32UCbnLghxtUpp9UocwleWo6k4Q+cDotchcwiih1\nepmjjB2O8AXa4V/xIvieHWp+y7eGB1kJU5czSf/vpLmVkAgCwP7JDvaMuzxPdZyL1oOAxantAAAg\nAElEQVRZkeaWZoiiCOefvMjpA25sjnlKZaeX4QM/fAgfu/IRe46DTNK/vWbNLpyxbK75XgFGa+tl\nCnsPtbHnUBvPW7FIV3MqeZ5NoxOYP6iRU7yaW5GAW14YZuFTMSlakkjQa6rmxhduDvGtg3iZDZLJ\nKcFb5UwSDodu5XImuc4kKm8OFPtG8nYrZR0O7V7mOWXl+3/n7i246TEbueHjXkxzM1EDtzJKHZJf\nc13lciaFlJfBPnfBl84zsGrvEI+QUTTPdyY1Es9wJUdZftpk21Z042mnYnqfJ2KaW8DpQ0L3ovbw\nZ+plmbMO81RTetapTs+5bjfwTlKlnLE/HTAQ6whfa0MIId+hc12FM+mq1TvF6/iKqFQxc6DCCPSd\nSd+668nCWutHvThiwZdWw+VMypw5F1rPgJtyHh9uHD6wZQzfuVuTqnK0me+kGxloGHLHPzvveOde\nV6/eWXDe0ZgYYoYpR8RySTMVRJhNdW1VKqmCns9dE0o/PHJuP75/71Z8y0ONATzNLbyehNKjdo3P\niPPKN7robxeZZI812R7XYcqwDahEaPdSrNpSrAajnUnud71M4Xe/fKdDYL9wyBa/0Mik3CCY6YnP\n0EszM84Kzs78+1Cgi6Mky9AYJCFkUi9TmO708J27n8SHf7r6MNLc9GeT5jZrziT385M56TfdR1q7\nFPQ6/6fnLseGPROiw838ikXEB1r1nEl8TK3bNW7aQGM/y5SzF3M91RfNmeT2/YleairNTYmvkD++\ncWjw1MwaiA4pQMSlDJmk09zkl5qUIJM2jU6yYGFxP68TGOwJugrgBl381PwyglzfieOPrZsFtIt/\nLk8vc5xJAWMiNH658NR3X/eJItlBS+/08T1FwmESjgCeDQ9RXc4k0mlEZ1KAUzckShjnVef5qEX6\nXZUziebbNLOvJtu9QtCoDjJpqm1RhbzdVF3b4Q3OL/fbJy/GESP9ohN893gbH//FWnwtd3CNB4J5\n1zyyC7c+vhfLL74Kj3lInBmWKnnuJWHeKBJT7CoqUsq8/tnHANBBHXN+FqbYCK5BBkkXfrdSwI/b\nRLsOzmBsqmtAGVwXGWglhoS7eN3ieLBOwGBzSo/9/waZxB+TqvdwWKDmTLJLVBRp7ovV2w/+t5FJ\nLkRYt2TpSB8Ota1y7zuNjELiIZP4YHGcSZTmxhYNPzrnV1c7MNVxkEl0Py4SVH+mZz3PZc4kGlwR\nIlEpoDY4bRQ2ds6ZRMZRu5c5iirgVtLYnKecLKeS1sw5UHiebmZy2Hk1tySOnDGRBaCMdaLJJs0N\nZdEy+zeNE0vAbZX9msh0I36aW12prOaWafJ2jjoYCRhvPEqRZsrZlGZK+GJCTgy6VqeX4YLP3ZJ/\nV77Y0SbXSuJCZTfANbToL33N4tgNbRw+wb5dtFVw8/Wjw5ISFkJEcb6TONJj1r+Pn/7Z8zaxybY1\niMamZLJ7KVKs7++iAwGXq02GtOv/Jd6BXqbQZGtOw0MmzXRTnPqxa3HJr9aZ7/3y6uY+nrObI0h6\nma1+N29QHrNcJnJeKSCc1uQLkccmFc5sX/w+8zkDgGoSfr+amyQhVIzkoG4msWNIS+WTfQkpwDwd\nkEd8/YgjX0uWzR/I26g/v/OKVXjx5291zqfgCX/nIwMyMqmbZnj6310rHuMICymlyJBzU5pbwJk0\nMiCPK6WUMTr9set8CrxipYCdB4rOAgmN4++nBWRS7rilVDf6G9B7z/rdMi+RhEwCgIc9lN9c1gc6\n7dH+RkJM9Nic9Q0gcq5xg5ALPz+EOgqdf/O6PWa+9lKd5vaRn63BFb/Z4qynhRLhAncUfcoUDosz\nyZ83W/L5YhwRQr8rpYfLwmGtE41NdQqOfvoZXV4BlYUHzG/Z34/sGC+kuZl9SEC3+dLuZkVnEkMT\nAlbP5Q5C0s2k9YnPozrBJY646Aht9QOvXA9JojBnUsR00PGZLi7451vwUO5Y4/NT6p46e0Qvtfu9\nc1/nHNdm2B+gktDtKHcm8f3D78sqZNJsODX9azecCq8u4jKCHLSksbd1/3QQncTtnRC6Vmqfb9Tz\n8c7Xf1o7pWcnZBLXHT97rdVjCpU9UT2OI+96HEww0e6ZgFXVekj7HDnYp7sprlmzq5jm5iCT5Ebx\nFFXexwem84I3Anqtkci6q9tGCkSEdZof3KvRkFd7gTq+3ki8UZv2TuDXG0bN59RzCnIH1lnHzgdg\nEaN0HjXdH5qhcZayeRMSGZlkf0HjkJ6J66aNOEJ/gH9UQrdOM0RZSMpQS3X5qLg8JZ1J/JWlmcI/\nXP2oczSKIjQcZBKwzSsDe7jiprnpv49bOOQ4gwrIJLbx89dHk31Of8PhMaCJzQef7330X/b+qS52\ne8gkrnzOH2xiSIhc0abop6QUzssV1ChyB6iT5uYRcPuk4f4zUZRFcmTRBpNmGTbv04rh8oWDXuqW\n3NYVS3VkzFRzy6/tk3BLFXpCk8/5OrLfheZjlvcVYBdcKc3NiYrV0EDc01WpIcqPVKWyZErhDV+9\nG2ewFIi5AQNK3zu/buZyUnCl199MQpxJtKB20sxRXMuQWlQNi3vro4g5zZz5Zw1rMc0tcJsCZxJD\nJoUW20EP4i+V1O0ZFI97Y86TEkXa+elvQIafJSVF332GyU7PzAsexeQVjUJoHI4qo2d3kUmz23x6\nHmdSy0MmUfuuyMsFh64D6PHL1wjurEhThaPmaQfFu16wovBbX5TSjnqlwogWwM41ft84jmqlMAB6\nzS2kuQnIJJ/rwhcad2XOJF98Y5NLqxE7RjFXTqUol75O9TNzJa/MmXT0/EEA5RFaGvd8fZzTJ69H\nP14VhsRPtnsibJyEmkBO8CCZdLDKoB0fqT92A4/nRxglY0lKcysLhDWSyJDdd3pFZFJfIzZpOb6M\nT3cLKRCS8HfYy1yU1OhEG/c/uR/3PGHTNDhnkm8AVSF8+FgKjUmSOHLPf/8PH8JXbtmQtzMLohh9\nv65Uwcwi/HLOthr+mh/dvw13bdwHoDhvnhiddDg5pGlF+zqli/3tT1bjjf9+t3OO7yymPaOO8Dat\n23XI6GndVKHdS41eSntlWcqDDgq4x/0gFO3VXB8s23v5O1q/e8I4DWohk4Q54gdeHWdSHOZMsgGz\nDHdv3IdNo5MGEepy/hWVjtkgk/xl0OdM4vvN/tI0t3JnUiilCLB9yJHdTr+aNDfvGQI6HRepmptF\nJsnIML7fX/WwjPodm+qatSG0h0p7jO/8pHd582N78KxPXm++LzOoyZnEx8FlN28EoJ0gKz78K+f8\nEDLpJIbii6PIGQs8+PHlmy0fb11kEv/9Tx/YLnAmcTtaflZCIPl0FhIyiY7HUYQ4LtcZKLBeNiYp\nYDjkof2rnGmX37oJf8WqeqZsHgOWn/jilz0NS+b0ASim1vptn2z3cNYnrsNNAQ671KznYWeT5Fzj\n84feK6Wj8oBpHEUms4WEps0BjlLPb1EPmRQ+eDjFRJ6SziT+mKlSTu4sICGTIiQBItjZioRMmjfQ\ndEvBexuAMbyVj0zSL3zxnD7HGTVjNnd7s2L+rPv5wFQHu71+4BN16Ui/GBUnz7BS5SgZUlAjuIsh\nR1f5yCQ/AuA7jAgqmmauU4Qic4Ce5JQat2i4D1HkOjIkoci3qTCVPzc3ZjOlHAi//V68pCPUtjJn\nh2LvmtpJi4FGJuUL7yxnYDJL5xNJnWpum0Zd8swQEuDyWzeZe6eZcsY+TzcI5aA77VLhXPAyhYw2\nSp5H3N9ImJLNrsPupRzF0zcclGNwuTDvjKFvwout77CVniGc5majCXGk1zB/A/KrNNlSxfr/yZyA\nG3CdST9hOeihVB63pK7rTGo1YrMZf/mWDVh+8VVeCk7xef00N/53p5e5myD9pgQZw5VO7ljpZRkG\nmgleeupSPOeEBeLvfZmY6aHdy0odZKTozWNO1UYgzU2Sc1csytc2+11TmPBVGze9g5Di5fN0Aa6R\n6UvTI+DmEd6Qosbn8mO7D2H5xVdhg5eCMNNNce0ju/D1O54owNc539HR8wiZVO1M4n03HOBM+rdb\nNwavM921RMJkLHOhMTzdydDuhTkYpLVLXzNzqj5108zuqWwV4jtfv4delHiaJAJuv22895qx5UzS\nyCRqX773NGLXUc8uHEIm+cL3gzTLnD7Ze6iN3//KXU7Vu16Wmffnp6pVaWN8HFYZD5kC/pUVPxmf\n7hoOjF6qHIQ3X9N9J0K7lwb3f1p/6miRn/zlWnznbp0O6aDH4gjf/PVmvPqyO0r1DNJ/KK3zkR3j\nWLP9oGi4c2cXf5wyXc4fU4+xqq+7D7YZN2DuTCpZnzpCmptv9JD4gYltY1NYLXDc8Xf0wR8/jM9c\n81j4YeCuI2JQo4BM4g7FcOoiNYMjFfw2NuKIBYfkNoUklBrj89nxo/vzqrVSFkGVM8lBJnm/Jf3Q\npt4pF3USGANytV/3Ox7YN+nweQtCyKQ0Uzhm/gAWDbcKKdCAdcgTsjHk9/GLDQCCMykfl1vHpivT\n+kn2TbSxassY/v4XawvHfvZgMbjB11vupDvvpEWGM1HbNvaYU2SEdSlfS79+xxPY5FVQJLuS1s2z\njp2HOzeOYvSQa5/x9SSEIqpyJrm8WnZOJFEUtM8AYKCl39/4TA9RJKf6U6XdwZa77/vv74EtY/j2\nXZvN53YvdflCPYQl6SZDfQ1nbPLnME3Px+boRBtjU13cyzituNCz3vDoHhFtFdIrJIJ4ciZxuyqK\nirQsc/JgA6HEuEzW4kwKHkI3zfDtu580SMw68pR0JrmogyIfQRS5C1iEIqT5cEXiTFow1Cp4aEUC\n4Ew5jSeDePGw60yiazkklN5g5IbwnL4GxqY62OOluXFjbfnCIREGTQNXV3MLDwdSUDX6gzmT2IIn\ncSZxmechXSxUtKj88EoaHWbQRuBRd3k2UMoc/Y7QALyiW2gizSrNTQEhjw6/Po0Zur+7MTMnWuWd\nvTQ3VER4vQhXmUiHQ2lua3eOOw49bgzNBBR3OuZv0HyT4ptnVV+YMcE5eZqxGPF1om0OJN5NN/vh\n/dtw0Rdvx805H5PDBcUMGqWUiDgC6vFWUPQ05GzT80GjK/3+ouf2kUkuAXfRmcRlUoDFAsC7vmtJ\npC0yKUUjjhxj9LPXPua0lwt/ol6qgs6kdi8VN8GQ0Z5mbrVJB5mUG/HNRlzJP0Qy0e6WopIAW/KZ\npzjFcVS7mt9gMykYMpIRUFXCud3TKKoQMslHXALAQ1sP4rKbN0CaSS2PgHvVFluVqN1LcWCqg82e\nY5m/lp+s2gYAuHq1W9Gm3cvwjm/fj0/8cm3B8UWOoPmDTTNHypZaEZkUcCaVyVQndfbsT/xiLT74\nI0uQTl3f7qYip9LV730+Fg23goYFT+Xqpgrv+e4DBt0Zej7+viQOLUDmVyhPc4vMdTspd6Dp3/gO\nLL8CZ519j3NWdVPloED2ChwivTSc5lYFo3fT3Ko5k5z7Zgo7DsyAqtqF0vILaW4CMonmjybgDvPr\ncDk43TXKPL/eMQs0Im/N9vGK9AMAkR3vlFLIeT38fc7XBRpJjLU7ZCSaf2fu0Dn/szcbg4mWrrJ3\n1e5lBb6qvgDC3UWbZTjvn27GNTWqYpFxFqykxN6vlCYd2kOBvJpb4L6mwlkaru7U30xq8QZJEgpk\n+ATc/PlIZ5YCCAVnktdmN81NPpcH4/gaQX/7w78s9Z2E79tFZJKMqKMA8/KFQ3hiX7FC4FFzdUCC\nsjFCyJq3fvO+wnf+Ok9t8lNJywJN+yY6+L0v/xrfZahqEmmouJkqrm1o+gJuoIq3kwfCOYL8E79c\ni1885CK3/HTuM5fNg1LArnEXAesQcAd0EKJKUMp1ZtD3fF7QWEjiCHFe8CokNOvGp7sY7muI44j0\nM79Aib83vubLv8ZHGS9vz0MB0d90D3IwthKX+sQijIucSfQueFo/F97+W1gWgG1zgNOPvQNaH8lB\nOsGoc6IoKuiSpE87BTDyxxkXCNJ9KSfgVvjoz9bg1ZfdGTzHl6ekM4l3gR/5BfRAbfLUhJLyn7OV\nq1fvNAONNql5gy7fj94AeHvtQs3fHxl7i+b0yd5MNtB8xww3ZhfN6cPYZBd7DrWdRYcba+edtMhM\nlkXDfeZ7GrhVnEmdNNXwa4RLY09304LCwIXzmTTiyElzC1UpI0QIITU0Abe78XHpb8YYyD3Z9H5o\nweB9EyRYqwFNoqYqlKe5kRhkEidIzQ/PljOJc51Updu4KYEVziThuX1nkmT4XL1ml4tMckq2e+eu\n3oVzL7nJ/VKVkCeWvIu25ygEdP9K0T76y4+u+HNq3U4doaVKcb7Bxa8XUjSGWtUGL+cl4EK3oxRJ\nKc3NVhghZJKX5tbumX73kYIkU8yJwscQn68GmdTN0NeI0UximxOfj0HJ4OVk55rLSDacO71MRNqE\nSIzTTDlj30UmaWOrGUcFozkkh2Z6lXxJtF6NMCdGEtVDJjVyQmR/bEtzqKpyBhlsoTEnIQGmuyk+\nf/3jopO42YidPfMBRsrc7mV41ZfuxAv++RbnN5kwb/z9giNIdh50FVdK2RlsNcyal3nRby40zvkd\nQs7tMpnqpM77uuI3W/CD+7aZz4YzqZeKiL1TjxrB8oVDQYP6c9c9ZnnM0swYx2kWdjnyfYjSM30R\nifsL882ew6u5zXQzc6ibZnlwzX1X056zht8upCotnmP1hnZP78uUJjAqOZOyLJjmJvE8cOHKt5Qu\nXyXbD0zLBgqb8/747fSywni0gavyyl++0PNxg4qnjVfpGRGigvN006hFIHAnkv7s6lCdXobfDRgC\nfM3va8R4aJsbfb5v85jT9jJndzuv5sb7MkSXwMechBgJyfVrd+OcT99QWHd3j89gbLLjjF0pzc1f\nN4k4Hign4KZf+Q5JLv3NxKa4OD+u3iRCVcT4PpdlPjJJ7+nSmu/vI/4YK0uTHp/u4Sertlnj1tPL\nQs6aOpXs/CBSfnkA2kiWej9TuqLzcQuHCoENwK6bFECfDcWLv87Te/CdoqEKqUA5Ebq08vPvfC4q\nev+jE7rQEMl017aTByD89dB/N36QjPQYvyhGqDI5FwIkKOWuZcSRJ6W5ET9tWuKMIztxfKaLkf6m\nGJyltTox+mbq/DYk/lzNvHWM+qGZxM7YPGKkH4C2rf3pS+9is+DY9O8p0skEkUlFwIjhTGLOxAju\nHkr6NQAR4U/oK2nZ+vWGUXz1to2lS1RZMZGQPCWdSVxSJTiTPOUpiqoN77ry2Wsfw8U/Xq3vnb8p\nn/TVJ3emQZJm7h5DXAmLh/vEKDlXYAucSWxwLhpuYaLdw/6JjkNkzQffUfP6TZ8MsxxU40zKlMjn\nYe9nIxNlKJc//OrdhjDNb/N85nRbPKfPLEgU9ePCyQ87vUyjkvKNhyt4viwYbBVKukqcSWFkkvw9\n/5q2P6WK2wZVB+Dv2TqTJALu+s4hwI2mzmZI03i88+ILxONSFMFPc+PILnqm2x7f63jQQyXbSXzC\n1e0HpoPGdNnjGdQZGzd9jaSgZAOu4s372FcejJMwP4Vv0ryseKbCi63PmcTlk7/7dN32QJqbYkqp\nRiZFZg04cq7e6L5115P452sfs5VGStLcQgikCceZJLeVcyb1NROtHOTf0Zgt43Chc1sN2cjopHKa\nWxlikI997nxPM4VeqlPq6lY0mmj3KpFJ1BaOTEriegTcfY1YTFOUYNVV/ut2Nys1BPoCxIxS7j+Q\nE3CzvuTVmtZsP4gt+4kkmPG+CfuZj3TlSu6a7S4qgldlM+XiVdhQtWlu/z1k0nSnF9yvKBU5irTB\nKY1HQPeXnxJL8o07N2N1zr3HURH+2OI6Cn9fx+T8USHh61UhzY01iZyXgF/NTaEZ2/d9Qk6OPOmh\nSfl9hgWH+FnHzsPJS+eYz+2eRpnOHdBcjH4KBaDfLQ0R3wAIVV+zbQqjsrnEEfCBl55c+L7Ty7Bb\nIPfmTgxfb9TIJPc7+phls6vmNtUpKvN8HSncR/G/9bwb9vaSTXutIWPTWGn9L6YOhlCedK9GHOFp\nR45g417XQCqkuZU6k/Q44LpVKM2Nj4HfPOGmi1QF1fYcajtr0C8f3oHn/MONOOcfbnD0DOmZy5BJ\ncRSukMuLjISCcQOtYsAAqIdM4tVbufDW9DK5mptExuu3w39vZXvIh366Gu/7wUMGpaq86/ECPIBe\nP3ppJjqZ/K6SOJP4SXKam/7/+EWDjoOF5Kh5Wh+iFO0qTlAu/tocItouQ+SF5hYg7+e8eZnzt7Uh\n9nkOKgeZxPQGP2X40ps24K++/wD7nedMytcdH5HlIpPk5zFE214glihVXAJua2/FUTkyidb/8eke\nRgaaeMYx8wrnUMZDN1VYu2McZ/79dfjNpn2Y6aal64U/7g25fP7OaA9oJrHjBD86p0fh852Okl0j\njUX/ngOtBOtzKoBHdmjdIKQruwTcLmcSH6dRBJO6Deg+ob6XEP5l1eU+9vNH8I+/Wleq/5btuSF5\nijqTbAdlmRIrbHB+oDiKnIVBqmo2G/lpzj9CA2iBgEzi75C4gbTzwR6gwbF4Tp9o1HGHUSHNjS0E\nhDQ61O45SjuXZhKbXhpgyiLB0zMlp2CQcDRNmfHz0NYDeOcVq8Q2z/OdSZP23qENPc10mVpaTLVj\n0B7zZf5Qy4wH63AociaF09OqNyWHtsg7/YVPW1K4DrWT8rx7DEbJu7zOduinuZW3055Lw18yFAA5\nUnrk3AGHLJYrjNwY4JsU/74qtQ7QY+SxXUKVIVUvDYanZnJkEjeObEqAEtNULcyYbk1KpL2fDxEP\noUT8am5czso3zFCaG98ANDIpNmvMZ//gTMM186WbN5iN0S+xPOkhMbg881h9fzcXXz6ZlIt2LzWO\nEXpmGykSUnHyktLU7jLOpNkQSqeZi5z0kUmdVKGRzCLNbabcmRRHdnPnToykJgF3XzNBEsdIU+Xs\nTnUrLnEZm+pUOJPK05N90Wlu8jl/9X1LXOnMZcGpUUAm9VIsyitQbfB4HLhhzB1UISVW4kw63DQ3\naYxzTjtCE45OyopisxGXGg/URu5gnmj3guOEGwbE7xeS8ZmeQRj6841fvRFHJr2IV3PrppmprgPo\nlAdAK/EkM90Mr/+qJXiWuKlefMpS53O7l6Hd1UGexXP6sHeibVBK5pyuRSa953sPOMeqkEl109wa\ncWzSx3zZIqQk8Oh8Mc0tDe5ZhNyuW82NKmbyMcARjqVpbtB70VCr4Yx/zmkoOb3qou/5T089cqRw\nnKquKZVHwMuM6l6Gbpo5upWUggWUc1+V6Z4k/N28+7t6PHGjCpCRST7qgs+jpMRBSK/I1+e59DcS\nmTOphu5jUcXuuS8+ZYn5O80y54XtK0Em0f48002x91C7nDMp0DzL1SbrStRXp/3dtXjnFatEPaiM\nM4lTC9C1JN0/U9o7aio4e7JouA+NODLGfaH4QYlQCuq1j+zC1at3Btf2w0FnABAVc/qqlcTOfssr\nI/vC09W4Q07q8ysf3IF/uWE9ll98lYNoAazd5TuZejXS3GjO+s4kPjf4swB6TW4k5ZxJdF2NTGrg\nm285B+84/wTnHFqr0yzDF254HDPdDLvGZ9DuZaKd++uNo7hh7W5cv3a3+5yZdQoDdu/zEZTLcv2a\nV4AlCe1Xn75qLb5+xxOFvrkub8MvH5aBFYDmiaJ32U1tIQPLmWTnaxwVq6hzZNLW/VNyKp3wCjbs\nmagEIlQFeyR5SjqTCl7eAjIpciafj6YpU76r5FVnHoVOmhmjCSgikzTE3d6PEDg+Aff2sWlEERw0\nEclIf8OZqGVpblRCFkCpM4kux3NQKS3J5yTxxRBwVyCT/N9w4f20eLjPS3Oz5+nF1RrWhI7QYpEB\n0iI8d6DJkEmu0cPfe2ifmE2aG1CEtLp8SnQvld8/r7bDbj7b9Ev/9LJFgZ9LC32IFstXAEb6G3j3\nBSscIzA0bw61ewbCz9EJdRxzAHDTut2F7xRsdEC6L/UhV0L7mjGrqsCupez/ZWOX0HF2o7TviafG\n+Me4lCFjaPMKbdwZa6dBJjGjmr9P2oT2sDRVQCsgoYgQRca5EyXUHRyZ1GrEaCSxUa7ICJPST/7m\nRw/jzd+4J+BMsg/Q7mWmHXX8K6ly4f/cGNbOqwzNpH6a219esQrrBWJPklYjxtYcoXPsAqvQzgqZ\nlBSRSVIKiFIKl73xmcFr/fSB7fjqbZtK2xoSyZnUTGLTl0tH+grHSbjxwddFUlp8A9AtFe86Zjj0\n266RcoUTQE5zmzPLNLc5fQ2tGAr3mO6m5j3SmJHK2wOaW6EsUkek6nxtmZjpBccJNwRDjhAuRC7t\nGz18fW0mHgF3/n03zdDI0w6SOMJpR2nnwYVfvM38drqbOo4KHxEDFPedDbsnMNnpYajVwKLhPowe\najtpcICuqhZyEoSKAJBw5b3MCRHHYefFlv3FlASOTPKHRbubFXQKpYCHtx3Aqi0HNDJaeBxpf5I4\nk/j45d9/667NhQBVFOn1jgd/nuDIJOX/r2q6uazeFEXAqUfOKRz3eQ/LCLjbvQzdnvK4C+utwVzq\ncFGFovtVBNz+vOHXCXH28OumWRbUGwZaiajn1FGR/UBQHAFvOOdY/CWrSKpREvrv4b6GIRaWxhzt\nz2/95r149qdvKLTr4HT5nOOioNd82rOldfq6tbtrcSaFqrnRt1Lvp5kez8sXys6kZhJjyZw+y5lU\nT9VEM4lM8PMd374f77xildnnfSkLIJSJmOaWv4vh/oZTTTctcVROdVK884r78e7vrkKzhs36hRse\nB1BMIZ07WNT7AFeHLUtJA3KkmjTOOTKJBRv7GklpFc6dB6dx46O7MT7dxchAE3MHmvitExaK5z64\n9YBxEGVKYaabinvU3/5kNf7sW0WOLJ9cnhwlHDUP2NTJV192J255zK3a5vNpkXzt9ifwiV+uLTh6\nyJbmerQvgy3Nt3b/k2M46cO/wv1PalTg6EQbW/dPFZBJlNkAwPE/7J/s4PmfuStcoM4AACAASURB\nVBnv+e4DBedRphTu2rjPScucN9gs1fuAcFXbMnlKOpO40KLDJYKLWIgQORD0w3Umvf7Zxxg43lSn\nF+RM4hsAYKMJxKNATpUdB2fQ14gLSvK8wSZajcRZzMoIuBcO2YExEIAYa2eS/g13JvFqUGXRobap\nEFPucXZ/46e5MWeSl+YWIkjPlJ44XFnh8GNfEladg/qINjNudIWcAXUezaa5FZ05nA/EXjN3ijBk\nkiR1fC9uWlz1+SQ8n1k87l3rtWcfg2YSO87JkJI4Pt01DtHZIpMWz+nDTevkcpv06yXCwkdKSdPh\nTEpEB6PEWcaNW1NZxLy78vYrFX6HvmOZC6WRhiKS9B0hk5LYrlsR3AWe1obHdx1yFJKJdphMlzhn\nppyUPflcej7iTOIpW+SICBnYt68fNYptGTKp3cvQ34yDvDFcskyBZ+H6aW7dXlaALVfJR3+2Jnis\nlcQm/ePZy+eb75Oa1dz6Grot/hiS2qcAvOKMI7FyadGwI7nywR3he5UYb5IRQCnDAPD0o+aa7/2S\n9Qenu8aY5SlgoTQ3wM7LA9Ndt4pdwyJLnTS3wDyie4QIuCVl0pehPq24S0owr2BG+kCIY6yZxAVS\nUy5+ZUVAk2fy23JEy/NOXGT+rkImAdbx4hvTfGw1kkis5tZh82LF4mEx2DTmpVdIyCTf2L/3yf3Y\nPDqFwb5EO5Mm2jK6OmCQVUU+ufLrp3VwacSx6KAFYNI1ufAqg37b5DQ3hVd9SXMPhZYWyYFtSjOz\nW3DUJF93P8bIY+meNF7oXTTiyONMUuZc/b+eW7/3zKPlRjrXt7JwuLi3cmfSnkPtYLEJQO8PnZrI\npJCUpZo59wo6k+zfHWE98dcYP5gXujNd108149LfSJwKaCR1VDPrWLHvcPFwywn4dVOFB7dqI5MX\n+pFSm0lX+PXGfabdXA5MdQy1RpUopX/fMI7yonNfuoek03BbTOoX6d0bAu4AMqkRR1gy0m8qeYc4\nnXyRKEV2eYWLSDqB1OYqkYYKNW+4r+HcP83CY2Wqk+Lq1bvwy4d3VvI7cvFRzPOEICLgvruyOQ5o\npKUUlAlxJvU1YrRLggC/WrMLb/vP+7BtbNropSEgxPfu2WrR8F29Rvuk3IAGZ0hiuN+89d7fNzgo\ngxBFJFVIWrfys7Wly5xJAy1doGXVk2PO92u2j+P5n7kZ926230dRhDf91nH4h9ecDiB3JuXPRQHl\n69YWg/K9TOFPv34PPnedrYj54lOW4hQPkfr2808wmQ9AdbBHkqekM0k5f6tCZCGKXCMzjn1k0uwj\nJ3TdoZxv6BmfuB53bhgFACwY8pBJyt18Rk2am/431GoYxaKvkRTg+yuXzkErRyV00wynfuyawgLB\nnSH89yHFqplYI8h1JlkYY2k1tzQDoI3cuogTfzHx09zGpjqaXyoLR4d0mltqFH4XbVM8P2Jk610P\nvcLfe8iICT2bYxjkbfjSzRsKGwE3lMy98g+NWJfk7joE3LNDJrlpbuXvgV/Z57vxxd8o6CxOKB1y\nwo5PdzH/MJ1JLzh5semr//jTs92DeSctmdNf+J0l4A6ludlz6fp//4u1pvoG56/w30UVV4SCCkat\njl80hJeculQ8Rkq2deAWz8mURSY1Y1bNLXLJY4l7arqbYsv+KdPmNdsPOoTKXMgwuX7tbiy/+Cps\n3BuGu1I/dtIMfY1Eo2y8NLcyziTia2qRI9cjO2z3Msx0U/Q3k0reGGoPH/vjTppbhm5Wzvk2W2k1\nEnzpjWfhDecc66BHkihcgIBLXyPJHXC+AiM4k2osp2VzabbBkWYSGcOYO2r/7Y+fhZOXDpvP49M9\n06c7DlqF26a5hRGDSrlBjqaTdq7/n32am52zUVTtiBnubyBTMrJFciaFSFWbSVxLmefP4pOd8uf4\nwIUrzd/S2uYL9WmpMymOPc4kfayb6nnx9vNPwAcuXCk6AH1SUclR5/9MKW2EDbUaJs1NmhebBPJc\nIBzpJeHcemVGSRJHwai9VHnHrZrrO5PSguORfwwFvHwnLEDE764eyFWzMtuNkEmAfRenHjWC3eNt\no+TTZS2aVevBn3/dM/BXLzopfHHvmaTUUW5InHvJTXhs16HgtSTOpNnSSERRVAudGkI6uIZcsWPL\nOJN8xO+kwyeozPVDa35fU+ZMmk2aG0ckI3JTKbfsn8I/X6cRJwtYBkMZMinUhl6mcO4lN2H7gelK\n3VFBucgk4kzy5oDvxJEe29nz6Fm53Sa8ewIJDPc1HMQjjZMkibB0pA97TDW30scxsnik36RmkoSQ\nj1UVJ32hAKWYVp0/+FBfw9lL/DWCCx+L2wKOEknGPQQacdX6exgfL1W6+iu/dId4jpMKqax+2N9M\nCkGABUIGzkS7Z9YgyUFEct4KHYAhvVLKAAjp64YzqQIlLhX4oDFaFkzi9wAsGhiwfSzpyoMt7Yiu\nYwLSKTxgRPcso0CgQhm3Pm4rzA22ksJeFkeREwifEirbVslT0pnkiCquRRTVJ/HzDWerfNOloihy\nvKc35yUAq5BJNvfTpr+RF7S/GTuGLQCccuQImg1tSK56ckz0inJjtk5UyEUm2WegTSLNyvPWu3m0\nM8Is0ty8xZgGaxTphSVTOoLtp7kBTFnKLAE3UK9CGZ1D9ycnmZt3LG8UdZ6NnA4bhDQZibCWNvU4\nijSZa2aV/dlyJvnIpDL+Fr7xE9qF/37FEms4+s9tlNn+amfSwemu2Sh42VLqg2cdN1/8HQC8YKXl\nB+BKg1LIiahheFhI5rA5SGM2jrRjiR7DGRvsz3vyssdzB4SNw9w7d/YEkG9lyKQoioLOpCIyqXgO\nKa60hhklDm7K1GO7DuGYBdqYfnSnLTVdVmWkEUcYbCUm4nHXxn0lnEkUUSHOJMvfRGOoLPXn4ZzU\nmcbgyEDTS3PTlR/7GrF5DhJpHfKdSfzV6NLZ2awj4mXS14hx7omL8I+/d7pjgCvUc/70NTXpsT+E\nJAJukln6lZ22zkZajICbP0sjjh2Hu3a46L95dbY6yCTAkj0DfkGM3GlbkkJThzPpc689U/wtCRni\nEzM9Z80AdDldenbaW8ZKCLjrwL65g6SMgJuLD7WXhPqizJnUTCIz/jkySSu2MS56+pF4yalLxWCT\n73SRHAx+EOKkfO8YypFJB6a6znrwtT/RgYGyFI4y4dXhfKOEz/MkjkQHLQAxfYVQN4OtpMA9wrmm\nJIkiGZXoI5OICqDdK1YFIikjp819CgDsuzgtRxASssQn4HbShiqGlEO2LjgOfSL6snfVSYkzyfbB\nbB1LEf57yCT+PJJeV07A7VZz+6N//03BYaerucltGmgmxinJ32idgIN1vFveHN0X8vmcDkPiTMqU\nn44sN/oz16wTCfO5EDKJ3l/IUPfX7ypkEr++Ga/CdXlhpeULbTCHmtGIIyyZM3tkEvG61UFezMaZ\n9JzjF+DIHNkh9RR1y5y+hnNvn/qEywHmJNg6JqfiSeJXySVdd8JziDgE3DXyBKU1K3UcUlYvkJBJ\nIc5Dsn/L0MaU1UKViEOgCbHd5EzyntFftyWbgKQq+JF6axC9u6lOiidGJ2VkUlPzre0VKqH6QjoT\nzUcK2hc4QgNrB3dGxlFUKHjViF1n0v9amlsURRdFUfRYFEUboii6WDjeF0XRf+XHfxNF0XJ27G/z\n7x+LoujCOvfzUQf+PhQhcpR2v39nS+RJAzdCsfT3CYuHnCplgEuwzCXNLeQ4tvBiCZn0zhecmDsd\nFL52+xNim3iaG1+sQ9H5ZmIjKA4yKbMbWilnUmo5k2ijrOpHfzGhfkqiyDz/vjyiGUrfSpXK0RFF\nAm5pw47AKsF5SAqHgyqwUUxWeKCpDbatbhs4Hwh/BmqHXxlotgbkYfD3ArCphPx+f3be8c5xSfgC\nHzKED0x3DSHiTx+w3EI03v7kuccF2/XcE22etO9EyPJoK3cyfeQVpziRaDIkmjmpsCHb9q7jixSF\n8FFlkgI10NQcCSFyxjgKR7CbBplk0YC+UCpeBG0kGe6YCPjunz/HzN3pbornHL8QcQSs2zleKz0z\n9pzh3TQrtOEVZxwJgMFzuxn6msT/o3mOOrlxV5YTf18O3aU14g+etayQ5jbTzdDfTHCsxxsjrUOp\nCqfhkvFchqycrbScMcbTY1VlVBew1dwA1/FVtsZW2R+htWK2SNvBvoaYjstTpQCdFkHHdx6wyCTi\nyvIVEn09+zeHTdO744GeTIWd95Yzyd6DExhHKA9+AHbsTXZ6GOxz+0hCJvnpXiStRjlnEgmvxuNH\ngUPJNHWM6OlOinW7xvGj+13eNjfNTeZM6jF0ASD3mb/OyZxJ7u/OP3kxAB2YWjRH7+t7xmdw3MJB\nvOzpR+D8kxeJiB2Sqkiv40zyUuIa3vOEOZOKBhi9x/5mUljD270iNw7/FBpuvkJPPC8XfvE2PLbb\nonp4H5YZJ3pY6nOH832KjGCfZ0ex39BYqiIJd5FJxX3wwCwKI7S7GbqpchxIfH/ur+FM4s4z3/n0\nmrNs2l5oDrrV3IrrSdfTxx1kEux7/ZPnHocHtx7A7etHTbsAzScTruaWGJSZr7dWCa/mRqeXcTi5\nyCR5zefpSqExduWDO5xxKYmCm61gCLj9+3n9vUpARUs2CX/nIgF3ZlM9B4SiMUkcY95gU6/jJc4+\nXyQ6Bi4nsLS62TiT5g40zXoibWn0leZM4ryi4Wty3sEQr5Mk4x5n0kArQSuJiwTcbKyEEMJcJHQN\nf/3c3upvJoU+fvrRc/Gipy1xKCYAu6/7ezQXqpJMfTebAFqaKUy2e86eAgDHeXqnlN69Yc8EOr0M\nU920VHfj+8YTo5P44g3rAQA/vH8bXnHp7cYJxqWvmWCi3cO/MxtfQm8Bdo2ivY72z4XD8vllksQW\nCUr2RBxHDiiman8W2zjrX3gSRVEC4DIALwNwKoA3RFF0qnfa2wCMKaVWAPgCgH/Kf3sqgNcDOA3A\nRQC+nF+vtmRK4EyKgCZ78f7iXIejgztKWsyR4UPxnnP8QiRx5EyQTNkKEz7Xj25vhMX5IBhous6k\nN5+7HEtG+tGII0zM9ApEYCR88nNlMeSxbTFnElcWVa7QlxlrgI3aRbDR9tDAp+tQ1ICEPJ9xHJlF\nfd9kB5kqGia0eWeZMlVjAK0o2Wpb8krsE3BbyGG1J94vnylJmaompbnxShjNvNy7lOZWp0qU78gq\n+wVvZ5oV+7g/wOGg76PP5c6H0GKaZgoLh1r4zB+c4Ty3If0uMZj4fPKdARS94qkgSU4m6/+mmcRO\nClIVf4GPBvzJqm340s0bzH3puXzpbyZQyi0DziVCFCQ5t86kosPLtFXptse50d01RjVw7omL8KO/\nONece+TcfpyweBi/XL3TSQsJScNbpzoCR8gFOVKsm2b44X1bcd+TYzZlK1V4x7fvM7wjZekn5Exa\nMNTCAx99CT544UrHyOikGdq9FP2NpEBCLK1hVJpbEoL5NmugPOoKX7e5MpxmYbQBl75GgkRQog+n\nmhuJj64x9yox2iVZMqfPzG+uL1NEkeTnD+0wqFqOTOqUOEO5jATSr7kjK6Swk6OSr1lumpsbXZP2\nLtrnDs30Cg5ejroiw2zM40yid1U3CsqV/9D64EsdB+h9T47hoi/ejmse2eV8z51Azdg6AtseEQfv\nGx/FIwWEZEe7+/nIuf15GzIszgNDk50UZy6bh6/88bPQ10iw8ohipbB3v1CTC1d1z/7JDq5evRO3\nr99b2JMTZ/2PxPczd6ApIs1oXPU34oIhLHImOWlqVvfg+5bvAHnZ048AIKfZkZQHrSwqg97PotyZ\nVKgcxgJr1jgvuTSsoyNCJL7/EHeYJO1e5iDHATeltU5BhDRTZi5z59MHXnqyGWdAeL/xU0x84VyJ\ngBtIjFme2xl5pUMaIzzdPaSbac6k4j3LSONtW62uQlf36wV+/c029X/BcHmaG+DqtWXBnkrJ7QLa\nU0POBv8er7v8rsI50p5HATNADpJwZJIUH2/EEeYONJEpjbi5Z/O+sqcxQuiTkP6/eE4fPpUTHUuO\nSRLfgT3c37DrSSBICBQd9WXpkNc+Yjlwts4izc1Pe2olMQb7kkKAg8+bOhkZko7J20/PSJxJPqJx\nsJngP978bJy9fIHzPe03Zcgk0lun83WzNYsAWpopXLd2F3qZMojaBUMtQ81BEkJRXrd2F6Y7KQZa\nSTBAwsfTxr1uavdUJ3UCTSS8+BXJ8QGOMJoClN5HuopUvIskZM9rZ5I+RnxajTjCjIOs/t9JczsH\nwAal1CalVAfA9wG82jvn1QD+M//7RwBeFGlt9tUAvq+UaiulngCwIb9eqXATWnu43U6LIg+Z5PXp\n0pFqngL+kvjC4ZOE/dYJemJwRbfH0tx4ig4RcEeR5ZOYO9B0lDcaAK1GjIe3HQjCS/mmyY2d5wQY\n8ZsNa5j6z9BNM01wW+FMAiyEGyim95lnyDuccr1JODKJHFH7Jzu5oeheg+5ByKSWgEyS9neeA99J\nlamKoj/bPgsZMSF4H1cm/PQxLsZQEhZqQib1mEHKr8WvxLlLuHBVowwiq69t/zbIJHbcrW7nOZPy\n/4dZtODIuf14Lhtf5xxvN4Xh/gZ+75nLHJQJdXHZuOJt9M9T0MreuR56qeEZE4A2kqIoMvfkTxOq\n+sePv+8HD5nPPmfSNf/n+ebYQCuGQrhsbBmZaJOluaWZwqU3ri+ckym9dsT5GmacjvlzHsGU6/mD\nLZxy5Ag27S3ykkjR+iR2kUkHp7uFviHjIs0U/uZHDwOgymR63FL1FABYt2tcfE4AeChPc2skMeYP\ntRB7CIKZLiGTYrzolKWOY1pMcytxdr/j2/cDAM44el6wPbMVrlhwg1+jTqt/z5FJXMrS3KpkboDc\nfbZpbovn9OFpR2iy7+ecYOdwErvIJIrQA5q4mJRDMuqqeEG4w5b3hUlzU2Ellu7Bu5A/ZxS5CECp\nr0k5nWz3Co50B5nUJALurqMsJmZt8Z3ccptHWTW4AgedMHRPWjJcizC+jBOBpJFExinW7qaOjsTb\n7zuvJGg//46a569p8xgPxyKGHOXPI1UKe/bxCwrfSdJJM7zzilV403/cg9XbDzrHXMek7Ew6bqHM\nw8aRSQUC7q4uXhBCOvE+4Ggkvoff8L7zccHTbOr2Ve89T7yWjxLgQ4qnAJEDeVG+PvYYkhxgyCR2\nrSqwGz3HZX/0TNGZVNMPCkDmTOJjIORM8vuY2sSLCcRx5CBwQmjyKmdSL3WDbi4Btx3jtIZYxBDp\nAeFqbgkrgc7v4qPpJDEE3LDv0+dw4rbBwhLOJHJucqO2jkMrJAq60iY5Bs11I3f9K+NNJOFrrwKw\n/cA0/u3WjQ7qunB/1t183tGansSR2V9uXrcHd27Y56CKQkK/+dZdm8Xj/c3EzO3pEoevH8Dpa8Q2\nbVE4n57HR7+kmcKrzjyqst3Uz1Wp3YC7XzRiHXQZzFEwXB7ZYfU337EuyZ98/Z7Cd9w+5dyw/c2k\nsMaR7uM7ZMhBUkjZYkLULD4XZx1JlTKOsAtO0WvzEYIPIBTo23VwBlN55dJmIPjD7UAJESihnv2q\newBw4uKAMymfA89YNg9JHOHWnGLHL6DA1z8eOHZ5x2yGCu3jSRxhJ+PF/N8i4D4awFb2eVv+nXiO\nUqoH4CCAhTV/CwCIoujtURTdF0XRfQcO2kmg4ZCuxJE7MHxFKJRjz+Xilz3NKCSkYCslOZO0ocs3\nZXIaAXAUrVRZRYGg4cP9DfQ3E7zidJ1ewhXYEIcD4E5+/nxHjPTjJ+88t3B+I5aRSYB1fpU6k1IL\nnSdFeYFn3Lz2WcsA2I3Ovw8pqUkBmVREHdAalWZuNbcosot1kDPJpLllzuTv1XEm1SBa5U31F2Fu\nKJn7epxJnZ4dH6EuD0HV+b1nww+Y5g47rvjyv0N7CVfmGkmMP8jf8VArwaufYTdBetcjA+48AMqR\nSfxY4ikdWT5Zzl6+ABeettScnwhpG40kRhJrBMWGPYdc5Vy4L2+nf5w+Uw4474OBZgKoMIdA5HEw\ncDHIpF5WgNySEHl/HHsGeP4/r4i4cLgV3Hx85BWglTqepvvlWzY6ZI39TVu9j0eVTDW31E3v+8ot\nG8V7c5Ecf4CudjXTTdHXTDDc18D7X3qyOSatz2kWrviYKoU3/dZxOO8kTdL4yVef5qBiDkfcNDc2\nT0qi1Fz6mrFIUN2IIzOHfKFV4W9f9jTxeCinf7Zpbs0kxhnL5uGeD7/IrNn0veSYIiWdUErtfAxU\npfyN9Ddx+wdfiJve/9sm4BHBQqyVUkEllox+/s4jRHjBysX53+7aITkUSHGfbPcKc3J8uguVD2VD\nwD3VcYJCIWQSJyPnsm/SzumqSO9DH3spfvGe8ypJ4z/x6tOCiDQuDfbuOqmLsOH38O8nVZ/kTkvO\nSceFggwT7dQgk/R59kS/YgygDbQ6zs+xybDuwwNun33tGQ7vFCnQxwVKitO46msmhTW83dNBtRDS\nLw44SXjfJHHsBCtPFfoAKCKgf7zKpjBSwBHQ76KVxGbuP7DlAH5w71aW3maRSrSfh9KkSNJM4Xkr\nFuIlpy4tNeDqSKeXoZe5aW58jIUi+UNeSgv1oePMjSLnczvgoOlVOJPu2jSK2xgBrUvAbfdrnw6B\nlnmqICVJI5arG1dxrAB2LGbK1QejgE60gBU08Nd8Go/cSVJVMbFMlNJ6vuV5JDSb6+ipk/7rG+DX\nrHERliF9yR/Pr33WMpPumeTIJAD45C8fxcKhFt74nGMr20J6UYg+RFc61X8/vrvIiUri938ziVma\nW3E80Dz1baJUKXzudWeW8opy4Ui9kPi6G6AdNr4z6eFtB41uU5cH15csd9Rc8Llb8HhO1B/nyCR/\nbNC9/DXHUpiE1y3qN0r1no3Ok2UK+ye7aCaR2aukog08FZ/L6EQHU51UE1cH9uteZkm3JUeyhEzy\ni3QAwImLAyACth+cs3yBQSn7yKR9LKDFdRmuOyaxtS+5TU6IWkBGoVXJU4aAWyn1VaXU2UqpsweH\nvA733q+O6nNnkj329vNPqMVT8PSj5+KsY3SkmxsW3Ns3p69hFIdh35mULx6LhjmpMCGTIoNMovNO\nzOF31DQamEvm9IkKH980+YbTasTi87USS6Dre8d7OXdKKWcSJ+DO2+xzRV3y+2fgmcfOM7mvPmyw\nmcQY7msgimAghpozqViljBa3TFE1N33NCJFTZcOXCHY4dNPMuS43XEJGTAh+vptNLt5LvvJCXa9g\nDS2XgNut8OS8Ktak0BDlX6eMyFuS0YkOPnblmvxcVYjOO8glvy+j4jnNJDaL8PyhljNeaLHnixaH\nvYaEH2nEUaE/rBNFj5c4ikx0nfOvtPLy1wemunj3dx8A70zJ9uftLPBkmPFl20Uy0Eyc8fmlN57l\nPk8Ufl66TjcLV3BQGTkiZXQl33CXjvQXONxIpDUjiaJCXjrnTuCVUzgpoK7mpjnc+LyZ7KR4ZUVU\njfcd38CJsJcUCa5wSqk/mTB+AY0EWPv3F+HvX3Wa+e5Nz12OOy++oLRdVeKmubkIvjpqV3+eGuhL\nFMFx4Ehy+tFzDeKVS9iZdHjb+JI5/QXDRYKPfzKH/ZPwyH0Z1cLIQAPHLBjECYuHnXfKqyZWV3Nj\nzqQYePvzTzDf82EiOSDJCXOo3SvMyfGZnlk7aW85NNMVyf1feeaReP2zjzHR/+ddchMAFJyCHAlQ\nlQI4d7CJ/mZSqYu89NQj8JLTZEJ/Ls3YJeDm0iiZW0eMFFP+ORoi9gw6kmMXaGfNyiOGnXQB7nfj\n1fxI+ppJsAQ0l5CzHbBz82fvfB7OPXGR4+yjKPfyADKpY5BJcRGZlKe5cUcRf418PvM0NycgElmO\nP72fye/XN+w2s5Q4ohMAgLecezz+/U/PNmvnd+5+Ep+++tECMgmw6O4q9TZlKcNVjqcqafcydL00\ntzrIJF8HpXZwI7G/mThrW5AzKSvX6+7etB9v+ea95jN39MSR1THM/uwVyJjq9ILzOYlZYQx2Sh1H\nDt3nxkf34KZ1ms7Cfx+8L7nhWEB35P38uettNkAIHXXSEtlg5aKg9XyaW5zgmvdFHWSSb4Cv2xlG\nNHOhX9H0PnLegPmSO5NGJ9r4s+ef4BQWCkkZyTKg15ayKfHbJy/GDe87v9D/jThmaYvF39FXUppb\nM4kdh7wvnHtwsMbayYXW2sFWQ0SbUCZBHc4kSXqpwpodB7Fp7yTW5c4kP12ehPYevxJbHZJ+X2+d\nTcXIXqawf7KNBUMtg3yUUyf1Nf0xMjrRNmluobT0XqrMWifZkH4KPSA7k3xErdH7maX0olOWmAwB\njjgCgN3jNtDFAS48uKpTe/XfZCc04gjveuEKrP74S3HCoqFCSn0d+Z9wJm0HcAz7vCz/TjwniqIG\ngLkA9tX8bUE4lDNjGy9JHLkGAD/+oZefUmsDbcS2MhRXVrgi9D4WTedeQF5KtJDmlnM8EXEWLUDE\n8UQLEU2WM5bNM55mPkF5H3Alp68Ri5iWZsNuev6C1snTbqRIOj+Hys/Sdfw0tySOcPrRc41S7Rvp\ncaQnKqV7zR1o6jQ35RrXStnFLc1UISefJORMJ0Wpk7oOsm4dZFIA3vfe7z1QuD6gUSbSvSUyxiTW\nDoJuaqvGVEVlyiTNqkl778srd2V5mhC/Kr93gTMJUeGcVhIZeOmCoZYzXiRnEuXTtxoxfvHu8/D2\n808otM9HJvm+NTpsHVNWwUpYVLGRWMV9bKpTCdWXnF7mvgYVl5l2kRBnEo3tlUvdVI4I5e+UOLNC\nyLMsRyY14sjhfZOYupaO9DtKDVc65oWQSd7cX7/HOpMGWw0T+dvDNqW+ZpxHYDNH6Th63gDexkjc\nJeFOfe6gOTTTw1SnZzbgMvQEkKe5Cf3aTGIMtJKCo6lMsaxjP3F0AndUaP6Mer+XnIqUvlgmIWek\nxGUD1Odh+t1nHIU7/u8Lg8ebiawE+gTpJMS1F5IRAeUDuLxyIYQfVfDiINNdjAAAIABJREFUjxYB\nQZ4k3qd0LxrrE+1e4Z1zziTaW2a6maPofuMtOuP+tKPm4pLfPwN//eKTnWuUoTrqRnrdfikejyLg\nFIF7qHCdJEacpwD7VcmaJXPr6HnFSDdHbVpkkvu7U48awZXveh7+z4tPdnhu3Hfivqsf/sVz8YKT\nF5eWgCYpQzz484PrZ7SeUPWz4nVtNTefg6fTy5Aq5bxX7jqOI1vNzXUm2WvEsW7DxS97Gn72ruc5\n1+etLiM45fveEXP7cf7Ji804meqkefAvPzf/P1Oy4SFJL8tE/eKBj76kUDm1Sqj0tINg5vtlAEEw\n3OeuZfQTvv4MNBMsm2/XntCYqKPXceGVjfh+3fCcsfTuJ9q9YPAxiQ4fmURt/cjP1phU7cL1HWQS\nr+bmI5OK63aov3yuGEmU0gEz6hNap6PIrVBah5fJ37d9lEZYX3KPO++KOZMA4Jzj59fa1wcrkHiN\nJIwsB7RDb8WSOYV9ktOISEu/SXPznUn5gTKEKq+KWlbUQJJh40wqIpMAS/lyuMikVClTnIPS/JI4\nKoxPwD6jjyrin3n/8ICo3291sotI9k10sH+ygwVDfWZtl94xbSO+njU60TbIpNB9x2dsiryUli5V\nWf6UF6QDiplP1BbeXF4t+vSj3X2Oz3lyJjWTyEHLxpHdIeaxIH0cR5jT38Tbnl+u04fkf8KZdC+A\nk6IoOj6KohY0ofbPvXN+DuBP87//AMBNSms7Pwfw+rza2/EATgJQTMz0hCugShWNgyhyeVWiCLjs\njc80UfQ6i04cWyeAj0wgecM5Flbpp7lRE7nnMM2U9kZGNmpnytfnI5kQIqQgPeOYuWZz45uJm/ft\nOpOkicKrufkDtpdXqyiboLxCDCmq8wX0Q3/LsvgXy83rPGfaXBYOtXSaW1as5kabd5qjIYzCGOX9\nmylcfmsxzSZi+aDdXuZERbiiIRHwHb9oqFauaFmaGw0VTvpo0730e+iyHH6XM8leK/gmeGpajWgC\nGf9SNTd+jyAnAEeWJLF5D/MGPWRSPv75Qkye9zn9DZy+bC7e9FvHlT2OdiYZZ5zKiaijvH10vp3b\nMUMyEQE3oBW5KoOft9MfCz5nUsPrAwWXB8s35stse13Nr1hFjSRVOpVMb8hh3jcAWDrS52zEfJPh\nkV9y4iSRJeA+YdEQWkmMDQzKPdhKMHegiVYjdmCujZinudl2f+LVp4kGNW8rj+T468vu8bYx/vxx\nxmXN9oPYPd6WCa0DjpkyNNzP33UeHvrYS4PHAeC8FYtse9gzpEJq14dffkqBOLGvBJlUpQg1EkvD\n+pbnLTffhwgqQ9BrX45ZMOgYZ4XrxHHBad9q6LQdafzROhwShzOJpSlzB3GICJWmR+Ls45GFosM1\nUrjjlRR9iuIq5Z67cukc7Dw4jV15uprDicickH7qgT+myhT7OtWc/GtKqXpRVC8KS4p6qxE7ezVQ\nPgePFIqROByOETmTivc885h5aCaaT82syayf3XUzwrOXL0AURUE0ZV2hZ6U11EEm5evJkXP7Hec6\nCaWxzx9sYarr7vUUVOPvNYRM4k5H7ryhvv6L3z4RTz9admgB5QSnnDOJhJ5xupPm6aX5uSA0hGIB\noOClASDn5LOfbYp6EyuPKPJclUm7qzmT+BziYzqUMjhcSHPTv+FIpoFWgnNXWL7EEAqmijPJlyf3\nW47BOI7wkd85BacdNYJnHjsvvwah4vU5U500eN0kscFVPufqVEOSnsdfZ/nc5etAkTOpOKdCDq0q\ndA4Ao+PQutrjaW7sSWtxJlWMRz8bI3ScG8FJHDn7YRLLQXRfqtKKqwoikH7q92EriRmirbj2GwJu\nD5H3+zm6tZnEwYJGR82161iddwfYOU3zabCViA5RCh6GgjplkuQBxh0HtHOWkHCNWE6Xp/dbhkzi\n75Sjtfzx/eJTqtG6JL98eAf2T3Ywf7Bp1nYelHrWcfNxzvELzJrso/pHJ9qY6qYYaDWc8cPf89Wr\ndxld/CCjpzlmgX53kjPpotOPEBFuXMivwKcGT+E+fdnc4Lyhvnz56Uc6eyS3s5aO9OHoeQM4njks\nX/usY3A48t92JuUcSO8GcC2ARwH8QCn1SBRFn4ii6FX5af8BYGEURRsAvA/AxflvHwHwAwBrAVwD\n4F1KqUpXtw+59LsyjnzCT13y+l/fcJY5XiWNODaDhQaQgjsI+YTh8Ph1u8Zxya/WAXDT3NbuGMet\nj+/Fpr2TZpOlBahpFCS6v/5MFSYA15nkpLk5zqREVPyllCSSXqodNmVKa6enK8REkd28pQhHfyPR\nVaKyYgqDRiY1TB8uHG6ZNDf+TrgiTqkQDWZEbN43hXd9dxV+6JVKtvfJN0D2O1+6XtsWz+nDC1cu\nqVXNLXQdzluQKc69kzuTYotMoYM1QQVGHAeQAqq2gJ5xyhWruTlpbj4yKSqe08yJmAHNl5UIY+qt\nDKlinEn5MSlNyU+z4WdkTKmmRXWILejaOab/bsSWi2XaI6CVhBu6vuFn+brse7Pt1X2VGkdTEYFS\n5sho5ummoc2bE3BzRxG/4stP17nNg62Go6y3GjE+/kq/kKZFGjQSi0yaM9DE8kWDWL/HOpOG+hqI\noghL5vRhD3MmKSjTblp3XrhyMV50ylJxrekPRKlpQ6P+OTjdNagGf7Pj8jv/eof+XnSSh/taIpcF\n9DucO9jE31y4Epe/6VmF4x96+dMcxBV//72syJ/R30oKHCB9jVgc73VSrJPYQu2ff5J1aoXSg0Kk\nkL5UpcNJ8PS+vOT8IgGGPytkkpN2nq+Rwh7hC18f4oinXbnvhTsVKSraEu4JAGcdOw+P7TqEl196\ne36+/W1ZeWJ/rEm8DdR/vpMt5Dzm/SKdE8ElmA7tZzQGWjkRrOMEKZkjEkqIPxf1MfXfp3736bjk\n904v/EZyCvN38nevtGmoZX1cR+hZaQ3mjgwyVDKlsGx+0Zk0NtXBQFM7zaeEvV47k+T2xbFFJjlO\n9IifE273C1ZaYu6yoBUhwLnQO5zqpjnHJTmR8t/A6hLSEuOvqXw+XPN/no8v/OGZSOIoyNkRkulu\nikxh9mlu3lpmCLg9ZNJgq4Gv5mu0hII5et6Ay5nUqzaKt3vIpDOWzcNV730+q/Tlct9MtnvBghuN\nODJznc+5Omlukg7go8q4fzl29Hw5zY1LCDUUQrhyUUrrQbT2+AF8c48azjsnYCqucVp8Z7o/juOI\nO55iF80cR+K4J3nd2cvwijOOFB32XJoVyCQ6dOkbzsLZLNhAmSyhoCx9y+3EC09bit85QwMc3vic\nY4NciXwdWzzcZ0ARH3q5fD5gnU7krAghtQmxEgrqlIlG5cE4kwgVQ+hMADhzmXWo034Q4kwCgKMY\nUpbrHEPePnXKkSPYfMkrsHQknB4IAOcsX4CxqS4OzfQw2EqMbsr30R//5bn4wTuei5OWDOOYBQP4\n6O+4OvTooQ6m2j0MNhNH1xqfcflGz1g2F80kwgGGTPrKH+m1S3ImtZLYZPG8NA8EL5s/gPdcsMKc\nY5BJ3rrw+mdrh89RcweM8+sjrzgF73+JRU8P57/VGRz2t3x9HmwluPPiC/BCtje1GrEZW1R9tY78\nTyCToJS6Wil1slLqRKXUp/PvPqaU+nn+94xS6rVKqRVKqXOUUpvYbz+d/26lUupXde7nLGyQFh1X\nAfMXh3oKvYWvhohf+SLJDRdefYRPiENMgVh5xBz0N2O890UnOW0y0TaT5mYnIzdwtu63OfYuZ1J1\nW/2NnDa+soWWCLgjWJirz5kEWGVuppcW+DSiSENTqT8XDLVMmptjsKWuszBTVkmj5/jVGjmnMwLn\nTFKOp/fyN51tCDH99LQIOlo20e5VVily09xmg0yKcmQSQ5WBb7SsPYEh6jiAaqTckLMry5TjfPGv\nlXo8PvSnT3JLBlWIM+nkpXPwjt/W6WzkqKAU0Kp0HF8h4M65v7lwJT708qfhZU8/wqTXaeNSn9ti\nxns3DSMeSEY8JCEXn5PLbzdPc4vj4rwpW1+aSYROmmEqWDUwJ5uOXSOJv7dLX38W1vz9hQBcwy+K\n7FqgFPCdtz0HN3/gBeacmKEChloJViwZxuO7eZqbPm/JnD4n91qpnBsizSxaK7HvwBceeXLSj/K/\nOaLRpLlxIzQwTiQnXZkjJaQ00/t61wtX4MLTjigcXzZ/MJhmmgpzLomiwpraClRzi6OoMgrI54GU\nSupLnYpgQHWZ7kYSicgkQCb+TJWLTPKfl6dL8WPU3kxVK7FumhtXiiK3mpuQTunwNMUR/vm1Z+Ki\n047AyiPmOMUtfAM2JD4Kzo+wApbXxLexgshP9gwrlmhUyPknLzbf+Ui2UMCHO9j9e/H1ye/vk5a4\nSJT3XLDClAMH2NjK//vj3zoOr2eIbBIT8Q2gxTiKu06aW5nQs6ZGVyo6L6Y7qVP5kqSbKswdaGKo\nr1EoXe1fAyjjTLJj+y3nLjd/h3RFAHjuiQtx8wdeAMA6k6RS0NJIaTAHGufk5GlutGiIKRwFHdj+\nvWz+IF5z1rJge8qEUmccAu46ziRvbabmOXMxHyfH5jwiftrWSH8D2w9M45t3bjbfhSq+cckcPas4\n1oucSSm6wvx974tOQhLHeeqzcq4zfZiV1PxXx9d/fqxAwC3MqZluhpOWDOPrbz4b9374xfjMH5yB\nb731HGddrhIz1zJbeY07vf1UUUmqzC1OVeD8zqcviW0V6CjyEZdxaXrnnzx3OS574zOrddCk3ClF\nP182fxAfZzyNtAZ1Uxl1bgi4fe6aXJ69fAFee3YREbJkTh8uYsTISRwZ55KPNPpD9nsay6ZSWmDN\nXULOpFkik/7yBScaZNL23JlEKLVGHJvg2lueZ21W2g98NA6f85973TPM3zyrx+eKogBQFcp1ASv0\nxDlfJZ1pqK+B2z94AZ693OWr3Ddp09z4GP3z/7wPcwea+MOzj8G6T74MX/njZzkZQIDVm/ZPdgrj\niu/LH37FKbj3wy/GMQsG8f6XrjTfk1/B/+0/vOZ0rPvkRYhjm+753BMX4j25P4H/No5du48j/EK2\nytvPPxHrP/0yfODCleJxSf5HnEn/X0svtYYvh/eSFAm4/UWqWpLYOk2kCLMvnDOJo1skIlxAGzrr\nPvky4xG0RqC+6dHzBnDGsrmYN9jCt/8fe+8db9lRnYmu2vuEm2/3vX1v5xzVQS11UndL3coZoYgE\nsgAJSwgwFhgRjI0xNiDL5ufE2DPM84CZGdvYvGHs8dj48QgmGAdsY4zNMyMwyCQjggClDveec94f\ne6+qVatW1a590r2n6dV/9D07VNWuuGrVt771o4fg/os3wS371sAr8s7yryQceGop6rKbGxV+io7G\npBAyqZGfItOkRTc3wj8hIZM2zYxpa/LUaB0ef/o0tFp2G9GJrdEEyw0upu1w4Jyetwm4t8yOaauz\nG4XNnPw/UyIKBoc/G86kFqBaqPl+chetT37xu/Da931W54sSZUwCWk8Rbm6ITGq1nI0/nWAc/m3c\nzJJnMs4kRCbVbGSSsEi+/cNfsO4V9Useza0FZpyP1ivw4uObIUmUJs9LEsKZlNibyyJ3RRqxiC+k\nHFHGXW1aYPNg8fuh+QKjflz7658Q7zdbGdojTRLbzY08U8mJ7AFsVEWilFY+WwBw0dZlsHHZqH4m\nTUwfr1cS2DwzZinomObs+JCFTMryVDDXaDlISmlE0g053X8jUoTOlahI0PnaZ9QW3XcDc5aETHrH\nXfsLXTlCvTSrL9eAzDlAqqmPM8mMSR+qKkPoufOdD5nEFWRfuhKPAc+Xb1JwTZAMAI2GjbDjCqvN\nmZS7uYFRyHFjHBLa5tRYqhQ3XFBkEkLZqYtERpj9jufvhx2Mg4iT/vqEt6eE9EIOAh/aMZTm3jWT\n8HdvuMJybUyUbeDzrdE4ZpJEOZsZ2j94OQ5vmoIPvPK4PjHft26pfBBXsNfAOrR1EbkfxhDlhuSa\n3ACM4Z1pee/MjVYblo3Cj1+2BdZPjziEwxPDFRiupl70CG1X+tlpovTveiWBW85fDe+57zBcm0fi\nxWe4/PJz9sIfvzzjT8ITdjTCvODIercALXf9r7E58fQ8GpPM/6F5i9vcfcZyn6uNT1CPspFJfrdK\nAICHb9kT7eaWpZGlxw0XuF79w1e+R8qDG1r5+zgnlD2/ZPrN6YYxDtUqmbFIOvzZvWpC6xwZEj17\nZ7iawkmPobLIkMpL7eNU4+6Dw4I74Ym5BiwdrcFlO5bDzHgdbj+wFo5vm4lCJqHgRhXJlQFsPTXG\neGdRWAj38Tbv4xodD2bOR+P3N75/wuWCCwwAjWiKcHPzGaUqiY1a0q7FaaLXn8efPi1GgZM4kyQ9\n8W23nWv9vvvCDdbYwj4KYLsYfuCVx+HaPcbotCcHISAShyN7UNDNLYYyA+W99x+B1169HU7MNeC3\nPvFlDWxAN7dUKbhq5wr4jTvPhxvPW6W5Uv3IJPN7igAUlllubnL0wiKUK3rPfO+ZzJiEh19lAg/M\nNVrwzSdOwnAttea2Tz36OPzgxJxVBj7voM52ar7pfDddK2bHhxwybQATDZ6XN0mUrgPUOfj4wb7G\n6U1SoheF6qEIxcdlMI1JzZbuaE1h4c2s1rYSat/3V+DqJcPwe/ddAGP1iu54MQSndJI4QXzxY0+N\ntYKdzzqvu2YHvPf+IwAAcGzrDLz+2nMAAOCCjVOQJgruOrwOPvHaS+Hll26xNke840gyzjY+6FvN\nOyOXuYatsGAnXr1kGN5wfVY+VACyCBj2+0opeNWV2+AP8u+azpFJ882mtVDSSbKZQ7p9YRu5KGWe\nmWs0ncUD8+FubgqUFUq6KA8Uno5x4TDXDHmhuxnwdQ/fgmajiQCKtHzMm0fDOrhhKXMpk1FOtHwW\nZ9Jozapb2v9pukoZ0sOicWRzJsncEQAAn/7K9wEgc6PD+hiu2ZGRfKfOKBYBN+uouME1nEnMqNMy\nm2jOmVSk1KNRxncShBtsjkzyGeI4wSm+Qk9KLWRS3Wz6trBNFm7yZifqFgE3QLZZn2829eaBosO4\ncAOXTiMvHO0rBpkU3oDQb7PKFVAOJZcNesrnk9Ac8+RJl4w1Iy60N8iVVIHEv6CUgs25f/qLPOTl\niWcO5xswkxdDE3nm8aGA4Q0ga2PHza2C7lOCMallG4O4skTrhLYT8to1W61CjpOUreO0P9HqpXMR\nlnlu3sxpn/uGiSC0gxkT6Zwc4kHifU2az5aMVCFRgptb/hvXdJOGye/8dUtg2VjdGtMK7Pb0KXiG\nswgcRDB9hxqasjDYCravGLfcmm3+m+z/IrfhIW2wppstuay+jU2svPSSzfAPP3MlrMo5kfDbrzhn\nFm46fzU8+vD1sGrJMGyZHYePveZSWMsI5DNkUgCBxuZzFEuXUwC/csd5cGTzNH1V1Pdu3b9G0xUY\n/Shbn6STdUSAW2VifU+jZ8i10AYhhEyiEsvJwqXmQSbxMXLjeavguYfWeVGWljFJu6vmm+eGvabj\nRo26m2hjkmdd4MEEXLSAygOkZL/RyCqR6tJD6wYzqvsMlYXGJFYe2+BgDq74uu8z0EpIuYkSbbx7\n9STcfP5q+PecXy7zTCiHTHIOMZ0nsisuMsn+Q4GCm/et1uWi80u1gDPJHDrGuLnJ94ZrqTW2MK1q\navrBP371+9Y76KJpiPsrFgcUF+oKC2CivVHBsUbXzhEWaeyyPB3st8NddHPDdQPlG3nfQFqL4VoW\nsfNZ564CRZCyuH7yAxvLWEY+9cbzTKRg7maveRELkUlZX2+1bN7gEvzdAJCNb0rA/Qu37BHJvJ9g\nEdrqBKEujX38Lgk5tnlmVKO5QjopBtvhe8sxQi9i6U0WMsmfblkZSGNSs9XScHI/AbcMDwUIIyTG\nhypwdPMynQ9A8QQEYHcGikyKeRfLnOWZ/U6J5ZHK0S3L4K9ffzm8+cbdsHZqBF599Xb7NLDA5xdA\nQiZlA6CI6JOfIuMp1oVbpuHePGQzllmKQJeobEDjM5PDVWi2kBDSlNlCJuUbljLIJMOZ1HKUO+0K\nxdzTlDKDzxfRjafvSwfANs5QMlnXL5worpSA22tkMtJoNkUDEBV0GWwQg9yHXnUxvPueQ1beDlJL\nnwbZxoBRjV6pa4MCjwJFT+XHaoYjqwjh50RzE7gjuOAbQxU7oleRMcki4Gb9WtcZcWVDOTnXgH/8\n2g/g3Z/8clZmpdw+JpQZyT2raRKO5INubqqYgBvANtxwhB8K3ejh4ivxY+C8MDtetxbFVqsFaaos\nI69Z5Nz8bGSSuY/zC51/sGwVzyb0f33GBPdMEmW5J2bl8M9ZyJGn349eOMMP8o1Folw3t0ri9guU\n6bE6PPrw9fCsPaus69JYppdikUk+BFKRm1uaGqNYTRuR8v8FwwCNWgpgK0ujtdRqRz72q2miCY9D\nQruXAkbA7ekzaDz1nZovHa3pE1lg6Ug8SOY5uw6+8YOTTt1jtFKOTGq0Mk7CQxttCD1N8o6DGaqG\nj/uqtWmS+xR+f6rcvOkmjYYerrMTbwCXIgD1l6J1ZkhQrH2GXu6y8J77DocTZ5ImyuJrVErBX7/+\ncvjNH9knPs8V9cnhqndzBeA3glUSJXK+8LKFBOdG1DGkk/Vs3eNl8hiTiI6R6DZ08+Xjz6cj8gi9\nsULHTZoo2LlyAu46vM4ZM1g/HMmJ8wjtkzif4BzEDRfSfGiiI8vuLNyYxOtqrtGCd/7Fl/XcgQeM\nPAIZpo3pU/fn4Woa5UIpiWNEZMgk/L2a8YH5jOCSUa2MwTBVCh66eQ+ck9NDZIcA5n4UMokeCEj3\n84uOoZzp/InKkJNffOu1cHjTNNMZFBzfNgNpouAQc1MCMP2A1scHXnncea6SJl5d6/Cmadi5yqBa\ncX6jLu0nGU/VplzHwv6dKGNAlsYp76+NplsvmK/Fm8v0jQvzACK4FviMmOglUsbNzefK+4MTc1AV\nXOWxWDi2+Riw94gm7b1rZb5gAKOP0IOJw5vcdqdULNVUaZfZY1tnnGeLhFJ7bFs+Bhfk+YWmfKUM\nT6k09v/0gYvgf77sqHP9n3/uavjTB45F7XvRywL7yU/m3FvY5mliv88NS92SgTQmARh/ymyQ8oVS\nJvxECdWf5PoTgy6iExvdLMYik7ibW0hmxuuOD6ROJwKZxJUlyfDjE5r25HDVcj0AMAMGrdR0APF2\noK5GloGmwZFJ5n4xPNGO5saVffzFT8QVmEn+qZMlkEkeNzdKwI2Cbm6+tKRyhvKOOUzAE4dmyywC\nW2bHMrJl6zlWH/lNK9pQJYEts2Pw23cfhMt3zFohuGm70FMO6v5WzJlk978WhMcqgJnIh6qpNak/\nHTDYKJVNtBoNyI1J+W9Ksv3nr74E3v/AMfjeM5lSiW6mlSSxFnsljL9Lt8/A/3xZ5uZQSxPHGEFP\nXQziKYFaWnyCb7lktFomWEDLfSZNzEJfSVxSZYNMsrlGWpBtYulpK+YjNemwZ8zjXEDnBI1M8pAM\nv+L3P6P/TpWCT//MlfDRnHcEIGygdAnn4+bisusrdR9EwQh4IfHZwTJ0Jc4j1FgTx5nkm8cLOZMI\nwmqIGZOkNDMUnflNN+j89BtLiN9VTbLogL/50S8Gy2QrPrabmy+a2x05OSUlL+dC0bwUReSLPsXz\nAAD49pOnHEU/QyYpgYBbntOlwyYbmaQsV05f5D7cYMhubub9NUtH4N4cESe1aWZMInWukUlhMQTc\n5ppP9+HIJLpBWz5Rd5BjXKRxvGJyyGsI5OHAJ4aqQXSUhUwi12PoDoqU80qaZK5UuWFeMoi4Gq1r\nNDfIpBb82ocegb/44nfMGBPyjTnwADCn3GXFcjlKFLz/FcfgLTft8aL5eFQr7LISMgmv8TVdQpdp\n3pZYZBKrLTSO/Mln/x0AMgRMogA+8YXvOGllLvf5xp7AAYerqXb54RLiZANw1x7uQo+baHfDLn+v\ndJ0fyHChbZYmCoZrKfzXew6afMmgOBVBCRHr5uYctHrSQV2BByZYPjEE//rQdY7BPnvXzUNEOidK\nyDmT33rBASsiMS0HGk1PepBa+N1KmX4rGWX4OJWibON4oEtMJbGpXVZMDsGvP/c8ePtzzxfTRZkd\nR2RSvJubT285Nd8U57Mfv3wr/OhFGzUnFB8DNQY4iBFcA1An+vXnngc/f+Nu5zlqhKqmCWxbPg5/\n9frLLFfyWFk/NarbnPLx0v79wOVb4dfuOM96b4xQS3BZPjEE+9Ytda6P1StZO+dJh9aVJcPZN2Lf\nfsnFm+HRh68nhws2wIR6gPzQI5MAIIhM4qdrzsIccOeiz2quG1bjd16wDi5gExZNkyKTYhsLnyvh\nuqqFTkpJYuc5MVSBi3NCzw3TclhoNCbFhCC2kSoqQ54IG8Y//Ics0hqdOHg7UcXFQiYRY0SjlZ1+\nl+n0+OyTp+adkzElLP54HSfCQje3AG+Rya7lGAaVcjlerIVWwqwHpNFsFir5lIA7FM3NhxCgryDn\nzaU7ZqFCOGHc6IBZnse3zcDLSDSAIsNqouwy+ZA29jvZ/aFqaqXvC4sLgAZXgybhBkHsf2jYSRTA\nxmWj1qZH55+43yUhJVEqqYIfnLD719+94Qq9AGFZ0sRFKEhikcWCqQ+KcqORlpoabeUiZ3CDNSv4\nbiulLH4lHepd4kyq+YxJ2TuNZksbLSTOpBAyoJIm3ihtRRI7hUh97l9+/hr4vfsu8D4vubn5Nv6h\nfACYeycZlj7XEL5x8huTwvN7JUk0YgD7TE0rzHYetUqi52YUevrJeTn47FLJucP++etPQEgcPrL8\npwKbm4yGyz1v7RJ49OHrrWtc8KQdwFbKw8gkk9/dRzfAq6/e7tTLBCKTBDc3qbmlOZG2k0pi3dyM\nYssNWbyMI1q5ddfmhK1RsSeXGv3IkKyScKMorYK/+akrdLSibgk/lZ8YrjrX+AZaC9uwFUnMM3Su\nEN3cBJ2Wj/HT+RrVagH82ocybkLdhkIZ+MbV16w+js8i8UXjdCPrXZM7AAAgAElEQVSdZs9xl92W\ngExCUmmc955g6yZ39QKg66fc9yZHapYxxVcPqMPsXDkBL71ks/hMqoibW8OsuEMBNzcfEbJPLN1e\n2Yc4P3KBIbX3RYuU5pciNzep/WYnhuCyHbN5QByTVwwyiZdA2q8BuGMHn0P9KWRoozqDtM4pIQ/J\nKF1Jk+i9Bs6z1ZQgk1i7YxZmL2D2GWL+ojHJ/p7bD6yFuw6vgwcuM2TLHJkEAHDjeau1i6+vn2N/\nLINMCuEdpPlsYqgKP/OsnVqn4GPAh0wCAPizVxyDjzx4sTc/nMe3rxiH5eNuwAV0hQYwc9TKyeHC\ng8Vffs5e59q6qRHdPvONljZG0rRedeU2uOn81dZ7aDyUqAKKJPH0fSo4Z/P9OzZTopRlAEwSorWf\nRSYB4UxyOUroCWb2237Cxz0BYNetz5j00M17NO8PCl3s6UISq4xJJ9GxYnFHJAnQ6fuBy7fCf33R\nIQAA+MOXXQh/+sBFzvs4ARZxJgHYC0OaKPgJNnjQePQ7f/2V7DeZOPjGk0KqaRXTzb3hkFFO/mL5\nlP0UV6QxnyI3txBCjJb1NE8HsB3ZqabK2pifbvsWLgUAr73GZdKnExeN6uLrZg2CsnF5E8xvl0PK\nzY8vavqUkW1yMfLJlTuXWyc5RcYkpZTVR6SxzQX711DVJp4PIZPwOSSC5sYkrItGs5lH1vKXQkKg\nuAEBzN/VNIEfPONC5jWaroHhVW3XQR+HFn2mScYJ7b6odNNIT5Ib1oh2YbQX5eUTQ5AoZaUZ8uW2\n0Iiky+DccGq+qRdAdMmidehz5cFNUrsEvtFzsXBtuJbCykk31Dim67q5FSOTQuNBKupwTZ6fXWQS\nJ7fN/i+DTBpmLiZcUakkChoNmzPJMiYVRAyqpgrmmq3CAwz6aYmylSvanm++yUTWiWlmGiXVNrwG\nkElk/nvTs3fB6iXDTvmHKqnoatZouoFCAGTjA3VTVGBHaPX1YR3NLVHA9wXcEIHrgD2/5P8rZaFg\n8NkitQR1B5tTRC4rR5TwbwrxoLUj3KVtcrjqzCGz40OanJm2M+0bFlkza0vkjIxBolMXPcn9JAs8\nwevE7meIwLHPn/w6Uqyb23gJcmaapLWxJ/3HFxzAdXPL/pciK6aJgtFaCk+ctBG9EoqQBoiQjLoK\nwOLQ8q3tFAH5isu3wQsFovQkMUaMuWZT62Ij1dR7OFfo5sbKQw8kFNBDcgVvvXkP7F6dGcW90SIl\nY1JBG1vj39pHZfNAWc4kK7BKy51L8JP5IZJrhAroYaSeaB2P1FL4sUs3w4b8YMEyeorGpLC+RwXH\n7iXbZ/Q38oiDmBL9Zs1lI2TjHky61BhD1RTectMey7OjSN8I6T6J8vcfSZ4Q+MNQYiJ18jWWtjsv\n5jkrJ7SroCTahaySWjrH6iXD8N77j8D+9Qb1U2ZduXX/Gufa+mUjuqwZz2+WXtGUPxpAJhWJOTzz\ny6XbZ+E5+9dofjcUNHZSJJJOS9npd0MG1pg0TVw0JCSATfhp3/dxT/BncX8tbdC42Mikdgi4s+e4\nElrmXYBsgvQt8ktHa7BrlVGiMcQkIpOi2NtJ2kopeNFFG61QiqGwj7wq6CkYVXaolRy5h5KYUSXk\nI03OWR6uWxdCr9/36a/Bxte/H770bTcqAz6L4rq52eU217MboTDy3Pj0sku2wK8/14ZMUqGf4DME\nzuWRSRotAZlE/nYI+JTZnKDwsvuQSY2GMVhYz0cs0vSRk3NNcWP4S7eaiBfaLadqE3CHkEmoKxlk\nEnNzI8ikIteGGGSSbdx03dwATBpzpO7sKB5y/jVr42Pq3HJz09GtFBzdkhHG3nV4vVNuNLLPTpi5\ndaiawP3HNzljF+tFNHp43NxwkzzXaGreBomA2+eigP0H55hnl0UwRC6cvrqeHpP5RMpyJpn37N8Y\nypy2O93MFpEvo/BNFtatdJJvlYcYk6o5dwSepnGjSZoo+C9/8WV436e/pq9RJf4A461Aos/7cm69\naprA3HwT6gVrjqUEKcaZRO5R40AoRDQKdYWw3NwqKYzXK3A3CfeOIvVLiRw1SSQ3NxmZJM0vQ9a4\ntzcTvi6F+o5Srg7BXekwOR4lCN+XUDpFBNyYls+oQMVFJoUNJ50K10kmvATcWTl8mzIazY3Lvcc2\nwaMPXx+1EUXXi0TJxgUp8AQvE+dMMqUHcQKLJeBOEwW/86MXOFGlJKFl57yd5rpHZ+BubnnNUkMq\n7QfjQ1VnEyttkHHtrpDIs1SUAli71BiTfPVAXURqlQR+TnChScjhINWfQuijQjc39psHEqpqo61d\nTn4AhCITcIcN/akPpQfKOSSNQiYVjAmcr2tsfuXG0dBySg1gdF6bGq3Ba67eIXImSetzLQ0TeVOZ\nHqvDR199Cbzp2buMMSnGzY3wVnKh1+65cAO8+PimKCNImpq1UUo3lEKilLWPofMlTetXbt8Ldx/d\n4LgRXr7DkIZzPjxJQgbVshw+I/owOSNHR6M+QLbGV9NEP9PpujIxVLXGu+aCFcr8wZ84rrmQUDes\nVRL47Juugl+69Vz4sUtltCMXibuWy541k/C25+x1dAnK02WNYmXSPcuZBCbE55e+87SIBLAJuPmm\nye3wv3tv5sJA00KlLAa6TAc8tU7HtpWJwhT3vP2uySQLh0wVOrkAX3roOnjHXVmkgRNl3NwKplq+\nWIY4k+gJiY8zqdFsWWHti/JXEP5+jUwSCKdRwfzA5x4DAIB//JodmcHOxS0rkLy5oT/Ri5m/ji3F\nUDDmZNfN3/PEzS1k9W40W5mbG6868pvXhy43ecblP8gh60McmSSH5/UZZv7z8/fDTXnkBvrE+z79\nNXESvYhwoeBYziL+mWeoqykX7GtYbu4vfionUWw0WlE8T0V8FIrV4dOCoQvf0cgkhhDwGpMoMqll\niOrp6SFFJq2cHIZHH74e9q9f6iKTciVnaqSm7918/poM+u0xDErtM+SJ5oblOD3f1H7euHG2OTfk\nvmwMWAo+/+ZrgoZWSWKXTV9dj9crzhy5aWYUti4fczmTPNHcqPB+8vbnng+//Jy9sHHZqHii6UuP\nb9j4JkpHACpwcwMw4+nUfAOWDFeJm5t5984L1uk0/+27z+jrqLRduXM5vO6aHU66jz58PdyZu2ZU\n8qhJIQQhgFtHvmhuVGLW3NnxIbg/D1l8ioz/eiWBf/q5q+FNz97lvCMp6RI5qkTAHYOyRLHXTGb0\n8aSCfSNVLkm0g87Nv0NCJiXKNoLGHKRleQjGJM8miBtyeHuF1sh2hCP1JoerMFy1xystA81fNNZA\nvF4nCYa/TpQSDQ8tnhm4fc8EQzAFxDJxQ6b0fmhzctHWZdr4y4W6QNP+YxsRzd9eziTWByRkEpWx\noYrm4USRuiQaNypJIiKXFACsnTIIU181nNbrsHwfIPtmjVQgbm4hg1HRHOwc2ljGdOrmZhtaLtk+\nA//tRYdg9RIbPSvNWUUE3BUBmYhlazE3t1Pzsp7FEaVU3MN/EBHgij0f2vgWGYn0cwU6VSVR3nVF\nkg3LRnPOpCwxJOB+ycWb4Y9ffqHjcaIAgm5utL5/9oZdMMb4SH1SSZS1BnAJJZEwBB+iE3evnoCf\nus4YZ27Ztwbe9Oxdzvz8zrsP6nEeE6kzND7KGjcMuXVWpqt3udF6sb+3a0z62Rt2avvA/RdnRqDz\n1i3R9Sx1t63LxzUXEhoP65UEJoaqcPvBtfCaq3e4LwmCfbGd9QZ1EDGamx5T5dP1ycAak5Cl/YH3\n/AN89JFvWfdoyM7st/2uZExChY022nV5GOkQ9wKKdwMU2QukTWCsWIoQC5Hp28AniTnxRLe8OM4k\ngN+79wKtiHPhVucQZ5K96TTXbWNSbiggJ6dF5Qshk/imnb7H+4XvlMEua0u812q1HKQRgHv64usf\nynPfNnYaZTfkjzufG+QchZKm5XFzk0K7o/g5k1ri8z65etcK+LWcKBAXToSnSigeCdI832hZZQ1F\nTMO+hAvRadaGiNST6oxLogTiSEchNH/76sQYOZHzQVmRQXybyCUjNR29pNWSFam6ELYbwDX24SYv\nSZQ28uAz/JswLal6+GbYXM/SPDXf1BBtyufE0+bCif5j4ejjGlYe97yvrpVSmqsP5SMPXgLblo87\nnEkShwEXXp6lozUNr8Zvs1wLC8iXUVxkEhqT5DmCbkC0K+JcE1YvHdbfi2vD7QfWwFtu3C0qrGhM\niqnlapLAU6fmodkKw899aEaKUnLvmb+RG4nyi6BgEA8apTC0BkpjlxtMamnmbssP7BvN4siUKNy9\nNWYerZJNJndZ4Mq/cXOTOZOk4B5FWgkaHWmf9hmTODKJVwtfIzsVbqCY9CCTsBw+Am75QnlBN7ck\nUfLGquXOQRxtj+tE0zJ25Rtaga+Hq6dFiBJ/tLcqPHTzHgCw+0/FM3/7OZMYpxpyJnnmqLF6xXFz\nk9pirtHM+7CHYD5Rlpub7zvxgDV0eEnJ6ilNQAh54dtIYzFw7K2dGoYHLt/qcPxoZBJ7MUmyaGa8\nX0tzpMRrQ8XHH4au7nRNOj0v9yMrkmcRMin/Lt6cIT3Kyc9jzORpeLnR8N00iUK2+vLHsff8I+vh\n3DUmGhnWWcbViZEv3XSQ3uCNz9pZKn96CCBtRYvc3ObIRIKcYptnxuDAepccWhLMO+T1g0LHB1Kw\n0LKUkUu2z8Bdh9dpYMLMeB1qaWJRhKAxybceFcnzDq3T0fEObZyCRx++HpaN1YkrbDhd4+ZWnjPJ\noPPKl127uSnbW0lB/MFqGWmPfGKBpZLY5KZfffyEdT9RCkLIJKnD1/gkDQAvPLoB7ji4Dv7vv/9q\ncZk8HbU8Z1LU45a4BNzyxMoFy4wb71jOpKNblsHRLXKkHG5YsMhEWV34UEvUQNNoNnNCShxUReWz\neXd8Rj4pChtf6L/y+DMgibLKatJpke/I3NzMd2AbuW5u9Jfb+CGUCzUAhZBJv/GRL8LfP/o92Dxr\n+x7TvLmbm3Qa5HAm5f2Hb6TRhbCdyRvfeMGR9fD3//Y9UVmh/RTzmGs0IU1MOXyheQGMgXX/uqXw\n8Ue+7fSFE6cb8JHPPwa//clHYWmAkBR9kV2DJf+m4v6oieGJm9uTxF02NI1cu2cFfOrRx6FFjF+0\nNSWDTVZO+zfd5HFYuOMmgQupMCJ9ZKx4Cp8hk3LOJI1MKp57YtwkufzLz18DX/rOU3D92/8i+nQn\n9NzEUBX+/Qcnnet83qumSSE8PciZlP9P29FXR0WcSbhW+iKV/a+XXwhfzee6mfE63HPhBrht/xqY\nGq3pORHd0abH6iJ5OwBotEfMmldJFXzvmWxzODlcg+88dUp8Lnii6jXEm+t/9GNHodFsiTxb2Pfo\nHBPqYz63CICMnPMrjz8DR7csg//0sX910CGS65JPKjmh63xO2k3nO1/xNAF34nImcQ4y/A7JcOZw\ntkRq9waZ5JaJC+fV4O1YhOgrK7zfTwxVHEQQ3SBzjhcUWsxOlHFqkJaMCxlnkvteJUlgrpGta3Oa\ngJtwOuWfKZE/r58aha8+fgJu3bcG3vfpr8Env+hGJ6PiawLaNnWPO0wa0D81Z5InmpvP7XV8qOIQ\ncEuul2icRvc0LgpM2HQA/0YQ6zA0/6QEDTLfMP5fPm677J68oTTGhuz/T7z2svw65exy3dwUe58b\nsqTxW+S67zMGKgUOATfnCEKpJAqQGZJnx8/Ls+8yD43WUgu9jXdCm3Z6jyJ1uX7i66co1VSJg7sI\nBc05kzSnZH5fu7mB2X/65tb/85Zrg3lJkiGTZF3NJ//vTxzXz1MdGJFJT52cD67lv3nnPu36n42D\nZmlkEgaHQok9cEHZtWoS3nLTHv17qJrCI2+16w8J52P2t5L49tB4tUjfwfWuHc4kk0fpV61o9GXr\ntR0ZUGNS2K9VKQgjk4RoQHrhUXTyzGDIpiH8lh6/oh8oKH2uA2QS50yi/SbU0XFwnTidTSSxyKSQ\nLB2twX//0UPw0Ps/D//y70/oxVMaDHRw0wWOnqzOExKxmPz5M9yggfXhGE/Ancj+40f/VU6f/D3X\naGahfol7EoAblc/n5pYUKK6uYcJIo2mUjVDb/cafZ+G3Q1B3l4BbOfn7Tr34SZcxiLS/KQhZ8Wkd\noivYXKNlXQ8hk/CbXnHFVvjyd56Cz3zVdmd8+nQDXvTuvwOA8GYKx6y72HDDi/mbkulKac3NGwJu\niowLLSYUPWDcUqibWyQyibQjzmf4jOtulP0vbnqsudf8bbm5BZBJvhkwJjQ3l+FaqvOIfTu08Mpc\nK+6aMlR13R/dfMrd8xlnHc4khyw7ycskl33ZWF0HtFBKwc/e4Lp4cXda0eWrEj9HV9MEvp8T0W+e\nGfUak3ib002X15hELofmEURB0PUmZADn4dkBzDg5unkaPv7aSwEARALuZhlrEmRt9VRuTI4xtNIo\nT9yQ5aw5GplEr7vzPQCp/wK9BNu+LDLpuj0rXGNS15FJzM1tpBpEZ4SMwEXcUTGCyKTT801xg+Hr\nKtVUAQJ1T+eoVVoag0xyN/gTw5mb6VyjCe/79Ndgc4DUFsC/IaVt43Nzo2PWx5nEEZ6+YDco40MV\nB03li3yMUR/Fsa8UbJoZg43LRuHL33naOyQ1MqkA0UEPs1BCASLuPLQeTs014X/+w9flsgvfYu4Z\nJBQOcTM8swucF68dTpSqRy9PVMYZFoVMYogqKg4CCXL9NU94fKgKT59uCOi8uPKHkUn+w+3s3USs\nsy2z4fGC/QCRSbwfU31srCRSOkaSxHjjiJxJLK9nnbsSti0f1+Ww3dyy8j15aj5Y59efu1L/jXnH\ncCaVjWjYqSBqqd3ADmW5L7kgoKI9Au54nYoLtmk2H9rjWOl5o3y6PhlIN7dKqoIDkfONuNHcAm5u\nQnox7ei1Xkb2Anxd8ncvfJedJNAsg/7D+eA6MZcjk9ro7JIc2zqjLdS4gZHay16o5LSo2w+AfdKw\nQvDrV4oZkxwDSva/A/MuMVhp+nONpkj27iPg9pEMAsiKYSwyKcbqHgoP7BBw4zt5/U2N1uD8tTbk\nVfMfcGQSiahSVhBFERo2Fr9O/vd8HnkNJYRMsnk9EsdV8cTpOAJ9H+EhLzvts143t/wyorpSlZHb\n01R8QvucFH2p7hmDfKNOCfENMgndV+w8Q26nPq4nnAtOSwTcEX0lhrsu9F4n0dxQfDDuGcIlAgBw\n8bbZQmNqDOqDKqG+Mc7z4UrLs85dCW+4/pzCKD4hwflSIlpGoaS1RVIhRPT7AlB6PmfhZl4pf/3F\n9pIbz1sFd16wDl5ztYHEx4x3Kob42t5Mc1ezZjlbkm5DjrCg+dATXspZxA+knGhu+XfUq+445W2H\nrxZpJdgHreifnv6PBtkts2PwH39kvzO3tHuC7BOu12ScSYKbW/4/NYBQ45FNBt9+eaZG5cAjJk/P\nvErqxSCT6HvZD9HNLU+wmibwsddcAu984YFgGX2h7ekc7HNzo7Jqia2jUZfbj776En0dh4tvHRiv\nu3MXN+xhEdJ88yRt3jB1nFd5f/9gjtbA7y86xKlq/aOlyxNyc9uzZhLuOLjWn2iR8SovEOpY2h06\nf2aIbdRj1kyepY//ClQJZFLAzY3PT9zNTROEK3NfSscnYc4kFXyuksoORUVrNc4ZeABYYQgyeghi\nOJOCSZYWzZkkGZP478Bchob2p06GjUl23ip/t9hQ1I5RpRPRnElt5uvdw+OaWdA3cK1ph7MJk27H\n8KgN9Mp2cwNl9iRdtCUNqDGJGUy40BMDSYJubsJrsSetclkiNzAdIJN4OjbkMzSxIjIp50yKcnOL\n+x787pAxSXqeSpoobeSQXvdFvksC36+j5gkhY2OFpn96vmkpqzix8KLxzbmUr0WciopRoP0aTaNO\nxRgCuW5PU57n9cEW8qt2LndJmNGYxDmTMPx8G5Pne+47DC8+vklzoklCNylbZ7PTlX3rllpjXiK5\nRuGue1whooaokEFAihDC0wcAq6Jj3dySRFlEmWEUi+lzkptbCE2C8tJLNltcEhyZ5JBjojFJGDk+\nMkw8oTk939TRZ1BxpG3KCYRR2kEmWWWIfD1U19ylE2ViqKqNEi+6cGNOzlp+ziOlAAC7HX3jKWX5\n8BP5NUuH4d48ilq7MjefIyAFomVdDhVfz9XEuLkhUaUkDqo4n2su2Dit7/kODIqkXknhoZv3WJFh\nQ5svyTjO3U4wDb6+lAm9DGDWTcV0GVqCbSvGrTyz5xXwcwFu1MFxJK33jjHJs55xwfWHBjPwzTc6\nmpGS5xbs5xggpFPhBzgTQ1WHr4gWgbYz/+5unOROjdaD91utVuG8isZdOlciSkQyJtF+vX56FJYE\n1leAzBXslvNXC2VITOQ1C5kkz03P3rsK/tOP7IO9ayad5ypWPYeRSZI3gR2cwLjejg1lpMWSThQ6\nnAPIiHPTRGkdwKeX4v/Gzc30e26o9KL9BAlNXZTnFPWE4aqN/B+qyGOdy6uu3Kb/5nMe/c0RDbGc\nSdw9DqUFLccN94KNU3DZjlmdrj70QAOMzl/MyhELmRQol+zmlojrR5HrGOdM0ocMYO/rskA/9vzX\nLdHGVGEsOn2Q/OZjDsfaU6fCbm5UcA6P4Uzq1OXqF27ZU/wQEW1M6rL7tIm0Fn6uTtby0nmU0Km4\nNLRXj523arMsRTKYxqRUhiKiZJxJ8oQI4E64AGZhDNdxwDDj5UwKJug81w5nUijP0AYSJzxcOGMs\np7GdEMetht0WvCctevVKYpBJQsYSistFJnGIf/a/Y0xqc3SdbrRsY5Jux5Z1cobXQ2TNNjLJvZ9d\nNxeaLfNSlDHJYxCQxCzg/s3E+FAVapUE1pBQuwAGTca5OmLknJVZBIlQV6R9Zc+aSfjYay6BFxxZ\nbyOTToXc3MxztVRZSCQAY1wFiEMq8D7G37DyK3Jz09Fost9GKfEL3mtSYxJpsLp2JfOncQEL94pF\n1lwsnk2mVD1Vz6mkRibNN+G6PSvhD158GFZOZuTP1CBCu9qqSXOy3a7ypVETkc+HDOYh9xi9hniM\nHFxCa9jBDZmBhZJjx7q5ceNSN+D0ekwLRMsmn/j8KqkxuGxb7nch4HPU9FgdPvSq4/DWm3eDUgre\nfNNu+ECOJiBvFebvk1DZQ9Hc6J0k8URzK9EOVB/xIf3edIMhaUUDTKpcY6yDTMoTsQi4hfQB6Pxf\n4OYmuPv4kKnIIeHb6O5fvxRu2bcajm2VeRnLCp2fK4nS+XPuJvz2GJfbTmSqwJDjQybR78CxQ8sX\nMiaVNcRX00RHLrLLoODqXStg/fQI/NilW/R139qilIJr96zUH2QTJdMDhDwdpWD5RB1ewvKWvAmo\nCke9FTYuG83d3ARkUmBTjTJUSXQdygix7CI9MJhrGCT6MOPoKuJUDJWPyli9QoxJWVv/8u174WWX\nbNaocZczSU7r5Vbb2ZnS9dveR+WBZUq6uXHhc8lzD62Dt95sDAR4YMMjfcbOn7Yhy6/zKqFuKons\n9VI0fvAdPJjkOiFFJo3Vw/Nfu9JoGeMBF1+kPAB3zVu9ZBj2r18KD9+yJ3q/h/2xiNy9G/K8Q24w\njZAYZFJ36xvrpkjfQYNvOwcRxpZUvuxN3edsgAktbzfd3AaUMylctUop6xSXt7V0wmuiuYVS9td8\np9Hcjm2dgct2zMJPk1CM7QqtndAGDOuBW9PDaZcrA6IRfPNmrZLA6fmmeD8zJslwZAA/MomKzwWJ\nG5PKzOu0KJmbm7t55r7lBmbu3+hZkVk8ExX9OV/Wza2NE3x8ReKKmByuwl/+5GWOcoxoshAy6f0P\nHIOvfk8mOM/KFt8gGG2RjsEybm7PMOX7KaLEhJQiY0wKb97pL25MfMdd+6x3uFtnNc1IV8PcDXjP\nELfS1hqq+A0AvjKjUC4W+/nsf5l3QF646pUE1k2NwCuv2Aq1SgIXbJrW96xTI1L4JSM1WL10GP72\n0e9F889xMVFO4vpU6LGYkzeebzv5vPj4Jrhy53LYRLhNYt3ceLrdOIXCTYNkPDH5KO89LtQta9WS\nYdg0Mwpf+vbTznNSHW6ZNYic5x9e79zvREcPciYJ9W/c3My1VCnnoCMzJsWXg7qmDtcSuGDjFPzN\nlx+30ti5agJ2r56Af/76E+WiuSWYR4SbW2RlYt3QyJi+OWtUc4bIaU2N1uBXbg8T3pYR6t4wOVzV\n5Rqpp/DdvMvZURN7e8a6dDTsbhriTHIfNn/iRlZyUWvHEC+1TyVNYNlYHT72mkvhmyQQgQ+ZZMqJ\nOgFde6nuY5BJf/NTVzivy4hQ8/GVJIFWqwWnAGDj9Ch8/ptPiO5m7ie5V4aqqeZc9PHqAGQ6KzXu\nYB9yoxUqq6yhdTi0sxmqppZbPwDA8okheO01O8gzdjv4kdDm72qSwEmQEYWWYQYyHZV6T/iiAvrQ\nlK2WH6WJOiYSJj+NB4LK+q9QYlzm77lwgx+ZJDxfiExK0ZiUjT0eBZfqz71yc0PibMnY4jskyO5x\nY6KC9730KAAAPPLYk1F5o3vfiIdTksul22fg2NaZ4ge7IJOIfu/yvI61VrRE4jzUCR9yOzoN5sc9\nuSjgohscgCgDaUyaIAqBJInyk8D6JMyZVPy+zxATu4EZrqXwrrsPRj1bJLHIJJzwyiCTYmdAXMOG\nC9zcaikak9z79UqqN9fafYx0fmlRUqC0SwaAu7Bgv3Hd3OJHa8jNDe9wziRqHLDTMn/TExssT6j9\nmk2jorSFTAo8qy3iOOl45pxlYy5kf67pKo5cdq6agJ2rJrz321F+aX4hAm5LkUqToCuDjwAYQOZM\nUiAt3KSMTLkzJIjZb2481UqJ92tMfs2m6d+0nJqXKKDw+6pb8w1xg1kAmWTzJdA8lCYpdt/xbTzl\niI9lJKYOLQk8uGf1ZHS+RfNpMJqbUpYhCcBv2HTmOE5cGixFnMxxHjQh0VjDQ5ZOVjerlwxDNU1g\n6+yYaExqR4nqBEYf2hRLfVRCaqWJ5OZWrh1wU4jJ3nFwbaxJxXkAACAASURBVGZMIqkkSmkSYq10\nJsrhv+MIUcPfJ7hDsEuS26wkHDERknolgUSV6y8ozzsU4JvxlY3kM0Fch0eqsvpbsRdl/aelkHcw\nqqYL3NyczLBcQntJyKTdqybhA597jL1bvrwyOspctNzcCsac5kSykEnmb/wOL2dSgZtbmih48mS2\n5m9YNgrXn7sSRmopfPT/fNt6JwaZVK8kcCLfHEuloXxL2O/pwR7nLXIioYaMSQXNxN3cuLgudnKC\nFhUGq3O6l3EJuFtRm+KQruF7Hy8bZJL/QDA2b+nrH334egDwuIN6+l8xZ5LK08yMjCG9sZtubh/8\niePwyGNPAUCGXHvkLdeKe1FnTbT2iP70Y6doNKLFIpN++55DcQl3QSZzLtBuRwlFKdJLOWl+GcGU\n2+kqqAekiUvAjSl3wxNKp9u9pPon9Yrs14qilAvP9MmhDVPwoxdtDHImxYgPhdFlJGOcRBqTcGFC\nY1KMwhH7ObGcSVUP8gEgM5AYNzf3vo+snJ6W+FAjrptb9v8Dl28V05SeBTDR3Mw9M0hbwmmU4+ZG\natQ2Yrh5cZlvNqOiuaGEorlx0SgDgrSKlRv3rgIAgLXM/a2MtGM4oItFSBGh9cD5NNw0mVJA00GD\nj8dFC8UipWVQWxOlMPufu7nVKsXzEkWP4WMSZ1JoLS0KO+872eIIxCwte2MdI/bGwj3FK5MWF0Pq\nHvd+aKN4y77V8D9eciQu34LyljV6+NKj17Ow2Pb9bsDpr9m9AgDCZNmmHxYLtvf66WyO2ErQRlTa\nMQx18rUxSEQqVeEQKlEuCXbbbm76ZNJ9NyX50BPMeRbmykUmZc9ayCRPwIeQmzMVXAPnI4xJSikY\nrVXaatvbD5Q3JtHvt4xJ7BRdOsDhn90N3TsUzUi7wwj3pL4pkSG/7NIt8IFXHofty82Yamc9LUKd\n2lyR4bRwTrc5k8zfvB9zGReCB9Bvr6ZKb4w2LhuB49tm4MCGKecdTjwrHmJWUzgZ4EyiIbexPuYa\nZtXiBh0fb6ckRa307Fy32rZcni9j3dyoOG7SHoOfyo3XZeZ3Lkr5N7CcMwmRSWXJgjlpuE+wGaj+\nTonAqRStoZQzSTT6Wm5u3YvmtnX5uBVVrVZJxHHLr1AdJ3zIGFdGbFPuOrwYBN3cfBQTnUpRHcW6\niovv6oPQ8mWnc6p9qNt9VBzAgCKTAIpdNizrdODZ95KNQaLCjRbqCz5+mG6Gf4wV6/SyQDlOFHVz\n6yJnkjae4GCQJcTBUa8khghR+A7RzU3Zftz8pBlT8bmI3XDuSnj7h7/gKa0rcw07vK/eUPFobvkj\nLlLK/N0UkEmh/kP19pgICWWQSfyZMhDNey7cAHcdXt9RdMB2DhGoEsF9+R++ZQ/83qe+Ap/92g+s\nE6EikvBQiFeDTOJoM389cxJAjm7iSDzD9xNSQLN7lpJGyhmDTPKNfd/45GTL9UqqQ1LHzr1U8Dl+\nAj1aq8BT+Ylzu8YkE80t7vnwQYWC/QGDipSvT8p+j68uaT63nL8myI/Qrly1a4U+0aVpXr1rOVy4\nZRncdP5q+J2//jcAiFOasF+ty0nfL90xC7/x5190nmsPmVT+HZOf/2WJwNMcQtkGVB7QgEZajBG+\nKdRKJVMKtcKYmLwdNzfPZlEKnc7rG98tRiaZTXWMjNRT8YCoSNqZA+iau4ugYaWIbgD2XGjHxKAb\n69LFiBLMTkpfmqPpOneauEhvX2EbG9qJhOkztOi/yyCTmm456N8GuSSvQ5wzKVHsYIektWHZqLcc\nDkBDrGcFjz9zGgA8iCgQkEmNlt6sFhNwe4tX2K9u2LsKrt29wqu31B1jUvlDRh/noVKo15ajl6Df\nlBF4h99HwyHq/mXHGkeKe59DhGYl0WNnqJrCkyfnvM8W5XlyvmHtBTVqHAm4lSLGpPB3dFNCiLzl\nE3X4+vdPyO+VzEfiNlto2TA9CmmiND9nrHzyJy+Dbz95ynsf67RoHcMh2I6bG+bRTl8xxqTAnqSL\npEkDiUwCCFeuUjKXQZHUKok4emLS8COT7Jffcdc++MufvCy+UG2I7VYTLnwlNWSDMYparIWUb5J9\ndRgyJi0ZqZrNtXRC5DkEpYtVDDKpTqz5MZtfWpZT8zJnEkdN+VwLfGRoeqIKtEmj2YQWZCTF91y4\nobDcvItKdcoNQLo+Ssw5vkgqZaQtZFJgVr9h7yp4z32HAcB1cwumGYAra9dFpry4Cqu5wPPjRNa4\nGZNQTz7RTdQipyDk/qGNU/DAZVtg71q/ixbvl/idZnzKeeJ1ikyyXYwLi6/lN+/cB+9/4BiDhBvl\nuG1kkn4v0rBVdD+yb3bCmVRGaD5veJbAudeDnS/WwcENU/CCIxuyCFklUIzYRxCZtH/9Uvir17vr\nYjtt3okLUmi8cXcQANm9PUmU5pBAaTTLcSYNVVKrf+DfCgB+794L4NZ9mdFQoyQIgokbsnzRJi33\nbEyfI5PQmFREwF1BzqRiZBJAZiRuZ45v5x00Au5aNQEPEaJfX1IWMom5uXWTsFSS//5X/5bn696T\n+iZt61PMbYd+XzvoROmVVxDkNq2novQlNzbbndBNkwo36py7Zomuo+nRmmUY3TAdMiZhf87LLaKv\nEr2JpBFVUSxkEuEwwr4yXJPXeJR2OZN0+QI6i4uKKkxOHwLp9KnBj63lLYhzjQnNo15kUv4/Rnj1\nPtBB3lSwXeg8OFxNxfIV2eTQCHpqrhl0R1VAkEl9tCaFuFd5AB2J6zVWRhahMWnTzBj805uugnNW\n+mk1JFm9ZBjOW7vEe18f+BfqefmesC03N70wl37XRHOzCbgzQu7s724uZ4uv5SMlVLetVlZhaaJK\nQctqHvK1GImN5rZldgxWLSlnIS0r1ilpQSesJkorgN1EUeF348mIb8DVPC44q5cMw5KRGvxrzqMh\nwe0lZJICsIh9faTTVAmrENcQ+vjW2TH4wreeEvNAmWs0WTQ3M3EUuUQB2N8tWa55tVnf38zQT9ef\nuxL2r3ch3W5a/gUFBTmsGPCkJ1FtQtLOJjL0Tq1iIkBytyCUkVoKqVLwJIkE5/i+k79R6SpSFi3j\nVYGbm/Zzzsul3Ud8llOgCrLZsNK+NFRN4VVXbfe+L5ULFyLtIseRSazcVJlvx80NADRcm/ZxSmba\nLscAbiZjX2+Xc4cP3yJDZbfmW44Ec12VupKNJZhkIq01EZMFRyYBgHhy2J57TulXtATdwoUdRUU4\nDEmV4ZBAycaTP+1NM/YGuF613RV0+krB0S3L4OiWLNIZHlpQdzjOmcTRHgaZ5HKL8Pq+cudy+OD/\n9xhcsHEaQoJ1M8cQoW+77VzRJWe4lra1mWpnXZgeywJEnLvG3hjw8YqfHoPi6RUy6al87ZFItIvm\nk5Ahrz0CbvudvWuXwJZZw+Nm989wWqiH+8idm8J9KtSY9BNXbIO7j26Al7/n0wAA8IortsI5Kyfg\nOe/4KwBwUX1UnNSF7KqVBH5wIkOnLBkRyNKJIUr3+0YL0O7EEX9ljEmdwkg5AXdMu+O36ncSV5/N\nipa51cYgLGgaFpUDhDiTsusTzKUx9AW//Jy98L0cRSbmHTLcCQe8w9VU3DNGI5PmGsxIb3Sz7DcN\nQBDf2H/w4sPRhnpJeE60TVYv9e9Hy66/q5YMFT+0AMJJ8bshvgMY97m8D3SSRxvvGtSybaJW0NmB\nm08G2JjkrwwdZjRRXvSKJLVK2raSICmaAO5gHKuHI3l0Q+jaVaR8VdJE88vE6GllN2Q4TxdzJtn3\nd62aAKWMcorp0AHpiwqRJgp+/LIt8B8+8kVHMcRs8N0XHlkPH33k2wRpYZ4/sGFKNCbRcTjXaNmL\nB4U0CkijIGeSVU65XqjQ0I8xEqO81ysJPHXKlMugXvprTmpnA+xTthOFEQ1UzimjxHfedtteWDpa\nhTt/62/0Nd5/qCKkXdGI8eTolmn42vdsyDBNgs8TuNEzyCTkCLPTDrmPaNdKaH+R4HWHhtq6JgKW\nFWLMm25MKx5ltB2xCLjbtIokSXYSE/t6p8YXfL0YmdSdBb2IAL4XigNHptFrMRFCcN5fN+VHEdA0\n+yVlOZMkrsU0UU40yfmGH5n0xbde64yvoUrq8DABuEol34RnLna20uOLIBrj5nZs6zLLvdEnK/NN\nBN+YPMfDcbRqyXBbrlftGJNWLRmGP33gIssQAuBHGVFkgbUmQ/ei39TSJLg5fPqUG0CiKNquL0w7\ngIyqKxJ3HvFL0VyGde1zgS4yJlG9+YJNU5pUFyCL5npQ4EeShBdTRGeTuloyXHPuaze3xKzP842m\nt2e4BzH+8vnq8UCka7XLmVQeIe47DEoSdFMrTiM0tosQGnLkPnns3bp/TTDvol6fJjaKfqjmBmTB\n54rSAQA4Od8UOdFokmP1CgxVE+93SkIPyNsRp9+TbrEmYEyKXX+rqYK5RgtmxxenMamXUrQkzeRB\nitZNtQ8iaUdXvPPQenjPp74Kl2yfhf/xd1/T12lS3dzWDa4xKeKZaqJgrkRl1StJ25xJXmQS62lj\nJSaQdoV+Q9EkSBeOkFGikmTw+dgujZthXMx87/mive1aNQn/57EnYK5ZDjXFjTBupIocjp8rXq++\nejv85b9+V+Qo8i369JlGsyW6uWW2JJdfhyuE1mdJ8NrAd4fQKpLw0xURmcTc08q4rsTIO+7a55w8\nSdLO5Onr65SUMHMfkY1JlVQ5JxguZ5L5myOT3nbbuTBSqwRPgXj7m3GCRqOm9TsmShJFIxnjn/dx\nUbibGxpbax43N04MWPcQcLfTjl4C7g4sC5VERRtVumXA6DZnEgDAu+4+AC96999Z13h9O/2vhwYZ\na7MhoEd9gpvKddNhkv5UKRivVyy0YJF08r1BzqSAmxs3/PBIQacbTW/vk9wihqqJVRbt5sYSedFF\nG+GN/+tzMDNe18+5bm4yMkk6QfcRcBfJsa0z8O57DsJFOWKqSH7l9r1Rz3Fp1wC7a5Xr4ss3p5iy\nFQzA25c7G1R/9frL4ImT/j7NjZFZucKGAb5JL4NQl6RMXRc9W2Qs0m5wEcgkPs/gK9fsWgHbVsjE\n1L5ySrnReg66uSkFkNsN5pqGI5NXRanAJ8K1Lz10nfd5Lg4yKcKW9IIj6+G/5e6V2TumFA4BdyQy\nKbT2xXImmXzxvcJsAcDP1yQ+q5Tg5iZ4CBQdyuf3T883xWhy+uAXsvz+5MePweoee6hQEbQC/Rcv\nh32oHZf+J193WceoukGT2Lo5snka3nX3ATi2dabneVHZs2ZSHwTZLvPEza2L1qSBNSaFFi9UEipp\nAnPN+PCSNU+UuJh29E2e9PLmmVEYCUBwuyWKLCDFk6BLHi0+l+bGpMhOzSHjvgUUN+8SMukL33pS\nQ/bLbFSsfFnr4eYYlX0kUTSQRfOsN6wq+42LUavV0nXY5ATcyjYOSHnYBNzhMgBgKPj4OTwGbo3f\n0sgNVe0aJ3xyze6VxQ95ykbl52/c5Sh6vpNbaigZqqVeN7dqqpxoFFyBlyL0aZJsJfd1+rPKjHUp\nQ+bNNWyl++jmafjcN54QlVpeDrqZKOuf7SCT0M3NY+zlm9uhCuU2iptTYoSGmm2XMwnfjV+Qu6MV\noau1D0HZzudctmM5LBmpwvefMa4JXHnmc35v3Nzyfiu4rcTMFXtWT8KxrcsKCTsTpeDDD14M33zi\nZHzZOjE6BhAcUrpVDzLplIASKVOssaGK6D7Nk3jBkQ3wgiMbrOe4mxsPDoJDvZ2gDSG5ZPts9LNS\ndK4Y6WQO4OJHJhFjErmuVOb292sf+gK8KIKjMCTTY3WYzk+sP/gTx+HKX/24db8dZFJI2qm3GLd4\n37NcsB5930C9CSQZqWUcYs2WfXgCYOaidzx/v/NevZJYYzEGmaQjNCoPATcxjCWt7H0axRANBnhg\nWcZAK90qg8h1yL8j3n3RhRstY5KPgLteSeDUXDPusMA6pLbv+dZDFH6wVRZZWwbxqJT9vUMezqRY\nNzcATx8nbm4A4KAkey0OypD8DiGTYuf/2YkfPkQSrsYx4+GyHcs7yKFzjZTOA4qkd5YzCcILmyGP\nVVDiQDPjTJLmgajy+IxJ5vqHH7wkvjAdCC1JMQG3uR+aOLINczPepUpvrPG3/By6sfD7u1ZPwJ98\n9hv6lDVWGdJGmMTOHwURFCfJQl+tJM5kH8qT10FdIuBu2SfE3PDArwPIJwKhw8j5Zk7+HTnTxCiH\nuMHgblWLjTOJbqDMO3Jl1YihIzvxN/csZFKSOMYkhzOJIpNSbFM0CGXX3YWbKBqcv4SNE45Met01\nO+COg+tg7ZQfwaF0n6PIpHItxhWgpsOZZD/Py02RSfwUpKzsXjUJH/jcYwBgI5M6IaysJEl0WbqJ\n5AkZk9o1evDv4HMKT7W3bm50/cj+j3EFuv3gWrj9YHGYd6UyRbWMstqJvaGs65UUQCJNlENqC1Cu\nHe4+uhGOk5PM2PUvI+BmhLqeA4w4Y1JUtn2TTtCJXHy9NIQAmh0fgr/96Su6VgaALLw3l3aQSSFp\nz5hk/w6lUFQ0iTNJkpDONVavwBMn581GyIMEovKx11wKf/SZr8PDf/Z5T7ruNXRzmxiqWmvO5Ttm\n4dtPnYJ/+voPdJlwaGUGXMJTSI1JrG5CfbjT7s2jubXjSkrfoe0xWqvA06fnI5FJ/g7hJeAuaM9Y\njcZ2+y7ub9RoX00T8fsK6UIomovMt8bwieVZGHFpCszfq5f4dctu8uieadLPqulmXkp1duDmk/ZX\npwUWqZNfu3sFAJhJJ01cMtKQ1Arc3IqSEiO7LMBgtBX8cP41zykEl7LKyLNyMt3dqydzvhr5OUQm\ncf6AFRNDlktgt6oRv/cECTtaTxOdgUgoy4RXRVVYPFrQslyTjGuB36BTGpnUKmfk4ZBnqa/jwjqv\nkUlofe+vOamd9uYn8Ch00zRUsYlf6d/VNHHd3FiSEtoM0UXSBpteB/ATcBtkkn2aWUmTwlMs/Qkt\ngO3Lx+Hm81fD2593fvAdLnzDiZxJNX1Ky5QRhvyjyCRr/mlDmX3ZpVvg8h0ZymG0lpr5vINJoMz8\n1c0Zux1lvkh4ks4psGtN6pmkQlt3c6poR+npxHhWlmNEr/nMgMoJuAHKzWkz43WLJ8M3t3CRjJcc\nbSW7uWX/87ZbbJuJDuwphYJ9zXZz6/cxSiZPCaegsVGqUOjTbc2dJV5phzNJktB8iWg2Q2jrHgBy\nWTE5BPvWGb6hmHexjJx8+513H4Q/fvlFFopKu6E3bfQT5S6KoRfQ9zqcrIcYD1rM+FUK4MbzVunf\ntJ9ZxqR6BZot2dDJxduOreIxFULRxIjNyxV+NlXKOgwGkMsXM++i0D0VtqfW7RdoOnVVAnOFczxJ\nUaXPiitE7V70Yvdfur51MY/uJbXwcjhXvujCVWYsXLJ9Bo5s9hOdFVX8F956HWxaZhOK9lL58UkM\nugbFB0e94hwbsl5lG+YiuXbPSvjSQ9fB5pkxqKZ+VAAik54+ZRao+49vAqUUTI0Y8kPtQsGGLn6e\nr3zuxiuBSqJ0tJREKahXE200iNkIO65zFXfxaLVsQkxTTj+KoNUyPu8YeaZoEWs0W9EKSAwyCcuH\nrhJ6wuzzjNnWSWqMMamaWsod/Vtyc+ObWapooMLEXSp5KXxIKACbOBfAdXOLkfU5ifF5a5dAJU3g\nV+84T4ygFBIfZ5IvmptDwF2NV+CKJE0U7F6dcZxYnEkdIZPi3dy6uYHupluOETtNm3BUiubW/TIY\nl043n4VWrjr53LKbbu3mxngKRTe39otFoieGn1PKRZVyNCS6woxHHNYsOmNSF8tz677V4nWf0ebo\n5jg+qG7IM6clN7dyyqSlB7bhIufqC/40OuVM0ukE7qNLrIv2iN/oa/Sk5lty30U3tyUB13KAbK7A\nuXe+YdMaUGOS43Yc+MZOu7fLmRRhTAIFL790i/gO/Xss19WfCnB9oVhuNeyjvNHckNg8f97h8onl\nTCrR1xOGTMrKJ6RZgi5k1yo3BH0rsq/2Svg+NLafLdT0308+qY6lh5sj3yFPWdlI7BIZMin7OwZl\nGCsD6+YmLQJ8kuaRm6hMj9bgu0/bISUf9ITPLjOeXL6K/o9GOmEVurl5Ii/dcXAdfOhfvqV/p2zD\nHCNYF6F2QCQIVZ5ef905AACwdJQYkwzkxyn/6UZGejfXMAYpHYrTg76ZJxHsXn7pFq2A0+ryLiDs\nss1tkf3fbNrIJB35i7ukkHpptVqwa9Uk/PyNu2DHiom8DHIRUBoleKxiuFTQqID1sVCLSTvjxveO\nRbBYs6MkWWSTaeK4fvA6ot0P61OTzOfPOidr1njMnn3wym2wY+UEQSZl97HPlEG07FkzCR9+8GLH\nkF1GHDc3jOZWkd1QsV9i/617kEntCqZBo7l1ypnUbTe321gkGcm9q+wGUJJ333PQQiq4bWEbRHnx\nezmErY3HIjE8dGS0KbnpljiTEqXEyFqdQMtj+24MMmnfuqXwzhcesBEbeAjCD2sW2XFjN7vY7QfW\nwtbl43DLf/xL6zpdo1utzPh21+F12sDdD6GHa6Zc8scf3zYDH3/k28H0ek3AXTTNFXEmoYSRSYxf\nM8LNjafJZ0fpVUQ4TxQYk5LEzH+U0kAp+wCL130v50mOMonRI+jmMnuHuv6bG6irS6g5LqFsi9zc\nEqXg82++xtGnYiMpltGdEuUGnREJuAuSpOsGBSR4ti19F97vY8f2Quxf//anrxAj4v3Sbedqj5LF\nIIulbWPkmt0rYNlYHb7z1KmcM6n77Tq4xiRh8eKcDZUAn8yHXnUxfP/EnHyzA+ET2YIYk6hiWzAL\n2pGAzPUrdy6Hd9y1D17yO58GgM789X3E5gCgkSCS8jRFjEk+RTxNFEAj+44Tcy6SRnqtXkk0VDdR\nyg67SY1Jnjx5lUpEqc2WfUKM17mbG00Ln6aRZxxkTAdTl/s97vehz712c/NsMnot7RmT5OtUsXvN\n1dstKz+PXOL2M9nIgs8DuO51IQQYtv/6ZaNw5c7l5BlUSstFL0TZPNMZoSM31MyXRSYJY6ATwXQt\nzqQOki2DTIpZaGPCpQN0B5nEiY35d9gE3O539sIggFlIkXMWyDPISIf9pIxUBU6xLtgPHdEbq4KP\nS5RyIj/yDXySKLj8HJsQlKM90Ch1JiOTFEGWUHEieEL/6+HVV29zrnFX5E3LRuHW/Wvgxcc3wdaf\n/jPn+TIIdUn4K6EUigylRQTbKKH7SHuAT2xZPgafevRxxx0tlKY7N7r5oYF4CUHGS5JFRVKQqOwg\nUOK85Pln7/nT7JTLxHFzi253Ww+S3se1+MmTxfumMD2DD5mUl0TZyK6yE3qZvp4mykFlS8auonah\nurXk3aIPtxdoOi3K90UXboR3ffLL7ns9Kk9IMDIpl9sPFHMs9lOoF8ogyL3HNsLDf/Z5WDs1An/9\npce7nv7AGpMkpYqjVyqB0+ilozUL+dItKbNw9ErsU4ZwASoBzqTDxMhS1s3NyiPxG5NWTGbEqsM1\nVwOnxiTj5sbSThXAnIsA0AuTkGeGosgWREe5IBe8wCT2ksSZ1Gy1LFcHEwI+hExyy8sNQDQcbllS\nPzdErfuMQSbZ0dya/sj0PZF2xo1vwafGvoMbpqx7tNvwE6osTX9+2kWNRWTjQq+jUZZHdcR2fv8/\nfdNKu1/iuvNl/9crLvICwHwTvieh8zoRVGJHa91ZolIBseOTThW+MvNvO+KGty4wZvaQgFtZ8yX+\nvbDaVWecSeF37ziwFvavN4geJOvlbm5iuTpoBp1+QRqJEpBJEdZEad1pLIARpUi6XRrp++xobq08\nglj/6uGqncvh5vPXONe5UXDL7Bj8GHFPCkk760koKqmTvlLwyiu2OusrChoQivpiqJzImYRt9sZn\n7YRn7VmpUdw+sfQzdk/KDXkNY9zcsDx0zKn8H0oZd8FOe9mQR68IiVL2mk33BPR9dDN8IsbNjbxH\nS9CCVuHm21fispGcAYrHbaIyN7f3vfSI/i40/NywdxX873/8RlSetN+unDQuWnpFXGACbi68Wt54\nw04Yq6fw9o98UYxYfFZcMYdnPXRz04f5ncuLj22Ca3atgA3LRnty8LfIQMzxIq05CTM4VFLVVWNO\nDDrD3bD3fzCWIeC2J177nqQgt/M11YrfqPfcg+vgLTfthruPbnTuLSUnQ7521OgQ7W5QbC2ukQ2y\nG+WAfnPc8KhbRKYZMqDV4m5u8nfQ3zQal1QeKqHTNp+4m0xXeDQ3sz3s7waxPeVXvi4ZiUw+MqRb\np8l+S6gmzZmUPxw6DUQD6eyEffrC22Z6rPuG7nbEuLn5x4lS7hjoVDCJ0YLQ8bESE82tFwa8sqS5\nMVLEfeZsmHq4BFn8Y7j+djBVPGf/GnjdNTs6KlMn31u0+frF2861otD53Ny6XS6dRsH9RNkuNwBx\nffBX7zgPLtsxC2vzMNE4T/V73i+UHvZlPX+TPFo5YXA/1ThuEEDx8e35JMbAGZIyryRKwSuv2AYX\nbpF5pbqCTGKcSUPVFI568vOl6RrIBGNirhNMFrq5Kf1/s+UnLubfFPrGTvtZO5xJWb7mOV80txHk\nTGJublKZ6TV+34tM8lwvWyccwRd8NlFQrySwf/0UXJojgNGd9fo9K2DHijjuSR7RV0v+u6mRSQtj\nnIniURSunTUm+WXQaiZJFGzIqTBuPj/jC7yMcSN3IoOLTBJaEhXBFjkF6ebGJkb6jSiQhJagqDwh\nw4oic7KkNMdKNU28G4w0UXDX4fXiPYpM8m3QceHgCrOJ1uG+hxtfaePQjrsCh8kmKlMubAJuZf3P\nrwPImzBffaeJcohWi8SJ5iYkrqO5MWRSv6Gc7YxbL2dSoCFtAu5iZBLdp3G0mZ+A21zZvXoSPvSq\n47Bl1lZSaD6/d98FsGxMhvr2W7A/OOGNye+RagoTQ0bx7sYUuGJiCJaOVGGsXunKyU+aqEKywVqa\nwIlmo6sbx6KT+I3LRr1EwLHilLfESXinedJ+oOeKNiB4QwAAIABJREFUDtJ923P2QqvVgl/8f+RQ\n3kVlktCdZaQsZxKuPzFrbieIqZjIVb68Y3i7zl+3FN5190H9+733H4GPfP4xJ7rlQku3UXZSfVpr\nMmR9qp9qHTcIoHAdh+pELz6+CXau9CN0usFB2EmkY5zDizmT/H0VOZNKGxdCB6ZCWrjm+dznzlk5\nAf/y70/o3xlKvOUdozFclbo8HfZvB5kUxZmkQJFZ2xfNDY15nIC7Xkng5JwNXQ/1N46cRKFublb5\n2P0isTmywvLGG3bB2imb7HnzzBh86aHrIEkUHNm8DL75g5OFeSaJgl+67Vw4vFEO4BTylOiHFB04\nAQBcvG0ZvP3DX4BjW42BVsXb5X5oZZEdt0TJ7tWT0VQNsbK4NIUSIinIuA5Rsr9+23YWAwmp7VZT\ntHjLRg5+rR0CbpRampFklxWKTOKGQhQsf40p9UHOpKrMA5O97z/FMs/Y4nBS5MoFRSb5ovHQ382W\nG5nNpwzQfsbfee7BtfD7f/tV5x3XkOWmq93cmvby1+8Jsy1kUv4/72/1inzSC2AbSURjkotNcsrI\nkUlFCis3JGXlMA8d8rgKLITUPJxJdGz8wf1HYO3UCPzyBx/Jnu3CpHvTeavh2t0roVZJutL3KhHG\n13o1gRNzja6exhX14z9/9SWl03Qiszhubvx+90UbTkVkUmct1qnxq5P3y7olaje3CDRwJ58VGw1I\n1IvayHjd9AjcfeHG0u/1So5tXQaf+MJ3nGibnYq93mf/8/qS1uVeiheZxAY+7as/lQctoUI/ox13\nW6ffBJIomudakc+F9OdxRCZ1wKHD9UMxmls+pn0E3O+57wJ49LvP6N+JUtC03NxscebjwDd2uvTU\nKwmM1FLNCRoXzc2/Z6Dvo9vf48/YgYuqqWRMstOnUrw8cF0j+kUAKIfav2b3CvE66jCTw9VChBqK\nxOljeHUWl+u3VC/71085BoaF380uXonxguk8D+h5Ht2SgbU7Sp2cE2Jlk0p/h8OiQCaRIhRt7PBk\nVXqMXuIb5jJSTZO2WoEy+he5e7nIpEwkxQONCyLSk4yIUFvSDX+t4oaTbzRbLMJHlhZHnMT4dIvX\nAwvmK6/YZp0uSO8AyHXDkUnJAk1m7QwjrKs6O9kNublZkUuEU9MgMon1PXw0xp3QyYeWqRcMviXl\n8KasfxsjKDNyMrQVVbi6xZnEI3p05L4U4M9DqXWAvvRJLziTihTDGMWxW0L7AdbvQuk9Zvy1n0bZ\n9VtC7PrquxvNUIxMkq4tvE7SqTx08x74y5+8rGturyiFyKRW1p/7WYU8oigKrjOIXCo6uKR32zHw\nl5k3iubWaM6kAHIJCbjLBhSg67pLayA8n2fg40xaMlKD89Yu0b9TJbm5Kes+laCbm/dOnCil4A9f\ndmFUXuYdZniknEnUmJQf7n73qVP6Wi2V3cdDeq0XIdylhcM6aF0kU58PddUvcek14gpy1s2tWAbA\nztMXGVhkkjyBZf8bZFLSXc6kiF6zUIrbm2/cpSNxhRYyLlXhZBXFOq3oYIObIcQ6qxefAoHKvEaV\nRGRTS/3IJB9xIJerdi2HTz2aMeJzY0WiwCLfBgBAfWaomsKDV24zKA6SSVPw0SjiipJEKfnbeF+Q\nmgSh2vPImWSOhbz59ULa6S9I4r5uagQ+9w0DQw9zJpm/+ckvgFtH9ITJRSbZRiWUGEV+6UgNapUE\nfvHWPYXP9kPedfdB+M6T5gTSUUYC00HvFJD2060kCuYKXteGgS4eQPSGM4n/zi6M12U3kF60h3Fz\nE4xJC6xddUTAXbKupD7TC3RybJ0WuW4PqtQrCcxODHU9XVEHIHMbEgb3k+ukiDNppFaBk3OnSxmI\n2umTJYBJhX1MH/Cy+bBeSaCaJpqHJ6TXIAF32fFNDVj8zdCBWlE0N52Gsg0kSoUNeUE3ty70s+2E\n5yeKgBsUUP3OQiaR92uVBMbrFfjuU6eta2KanmxbrbhobqH7RdINZHS3hCNL+olwlMphLsS9d9aY\n5BfTtmfNSQCDjEwK9HHDmdS5EaOsLJQx6flHNogwyyIOCFxoRWQSueZDKMRIxXN6UUZ8p96YqmPs\nCoTiNG5uUj4kbU+R+XXXmKTg1HzDuSa9X8SZ5FsY06CC5Dlxjeib6B3G3RL7j0wq31+2zI7DL912\nLrzjrv3Wdd9JL89HRCax2pWQSZozKX/U4R4rLjoM11J45C3XilF8FkJGahVYNz2if5eJSLMYFZA0\nUYWKHA6pdouPUYX2rCGn1mWP0SNEQr790Y9dCB9+8OL8Pjj3uy2Ypj2XZf8vuGrVwQd3A5lE2+e9\n9x+B9fk46mSjiEb+orElu/8vvvFYWnr0CRaiLM9EWpP7OaX5jElbZ8dg88yo5g4qYyBqx6hdZh4v\n6mO4bnJj0WffdBX8/c9cEZXngfVL4cIt07Bm6bD3GUnsUPf2PSk7PGCNdW9CPj4671m6s4OG8n9j\nt/tZ7Ninz/nc3AAApsZq8N2nbWNSEbrPilgMtg4lSYzBr0jefNPutt/thbSMNWmBhOsMcQVZhKrc\nopF+9K1Bqv4zDJlkX0sDIenbkZi0FhukvEjhqATCmtNLRcSJIaml7beDUplCxyMFrZ8egX/77jPw\nrSczyG2VcTqFCO/qHh4Yfi286JMTG4czScEp7kOeyIsrzaIllNdXhkqB1Ut6y1FqhL7aaGblRmTS\nQm0Q2x1Htx9Yq130UGLd3GIIuKk4yCTPOwsVwSNGPvVTl8OJuUbhc2WaYzEak7JgDOHvxPHRbumP\nb5uBj7/mUssI1ws3N1DIy5b/VGC5XZQJ6d2pSMikhRKVLxadFKPsWK3q9dNcoxvWVUuGYBgRw+0X\nK9qoIc2bC90u3ZBefYO4TpI6RC6cftah7/Djql0r4KpdK+DqX/14VqaiuSVSl/FJKWNS4bNyPXI+\nw9B8uWHZKPzuvYejy4RCD1RjXICxTEs9BNxcEqUYqTTfh5QwJkXlGC8x649SAIoU3+fmBpAhqL/y\nuOGLqlcSUX/wZdtqtUojOTi6J0bOzSOyLfTUh9k3F8AoTcVFM8e9t9D1d1YGRwbWmBREJuX/d8O9\nqqz0ZPPQgRRtyqtJnGGloiNWlZdqqtreUC8ZrsL3nplzynffsU3w2BMn4ZnTDXjnX3zZ8NbkjyGU\nVlK4agHOpHaEGysUAJxkyCSfUY8qN01hI8TfiyKyVB43N4e41xXkeULliNdnv6STYcRRaiFjkk3A\nXWygttzc8nsV5irqnKwtrinBkljXkTJoq25/7/LxrIy+KEcxkibFcxDOFZ0Y/6ghCSAcSahdSZSC\nSmJI5ouMRz0xZuZp0vmpWwTcnUo/h5tBJskb92qaGFRIBwWLdvEQ8lgMQUE6lZ4Zk4Rkbdfz/Lme\n5C5L3YNMQsH+VMQ8QMvcHgE3Sy+QRFHysZvpXqDo7IM3lp9QoOv2ZIEfYtfGJEHOJNvVjd638/Sn\n1e25OqY+FdjltZBc7PWp0Zpl1KmmsjGJ6qeX7ZiFn/3jzwFA1g98yCTfuqEK7otpRT/ZW9EkzQtc\nonYPmM6Eg4heSTtGznZloftPjAywm5uw8cM/EFLbASJGkljOpJBbTb+l0JhUsY0wVKQID+3U5/Xn\nroKbzlsV8dxK5xpCjTlCZqiawoNXbYep0Vpevnhjl0YmFZziBqNukL9rqUsU7CKT7PvS39J84QvN\nKUUoMb+V2E4xCwp+/1yOUFo4H+/u5VsPaN125I/s799/8WGYzvsVL0XLOsHLjUkMmdQOAfdil4V0\nc/vF286Ft912LuxaNdl2GpW0uCdrZFIXi2+FWe5SwgqKSFx73/8wTR/KciFEKlOs1NrkBJTQjNyY\nZHiVei/SmrbQ7dIN6d0nuP2X9p+/+7eMF7GfroJDBfojHpaUmU/aI+DuXvpoCFiIzWlQVxKKMzNe\nh+cdWhedfqJcQ5LNocafj9MruyFRfUT5+VF5H0B9W6fvbffs+kM374G1U/YBSzFnkp3m7Qcz+o7L\nz1nuyUtIC2kuot/orSy0lxvP9ywBd+eijZy9NPQMUP0vHqtHSQlx/GDjTg5XYKwL0T/KbKhTIQrR\nQkqhm1sAmUSvJGzDXEZu278G7r94c+Fzv3nnPic05WROgsgXILNxyP7nqJKQ4S/s5ib/bedt3+B5\nJ4lykEk2sbcSr0shiIui2AHEzzd84Zf69R35wj2HrmJ9tL73SkInvdKJ7eFN0/CGZ2Whlnnd0mrA\ntkFeHB/nzpmwIJfh4ek2TdDkcBWeI/DBlZEMmVT8DEB3FT7KmdStDWmiVJADpR/IJEySzincFbnf\noo0Bbbz7wVcdh3fcta/0ezXhMIbWSSVVGv3bEWeS5gAMp4FzDeWVWWyu9+1Ir+ZQmTfRXPzEF74D\nAP3V6X2cSSjo0t9rAm4AxiEZGFlF7fOG63fCcDXVfE/9FBpYwwQJ6J5xi7u58RQdN7eC4CndlKK+\nBJAfPpLfIRQbNyb5nsQkpO9peKBJPoPLrlWT8OjD1ztGqZDoHBZY99IGB43MW5jyODpB7HtdL8mZ\nI/1EJg2CDK6bm9DNNV9O3rivunI7PHVyvp/FgjRJYKiSAsBcX/P1SZHCIXE+oFhQXeHUrh+CyKQf\nnLDrU2/c8zavMCJUDCMrKS/oE1+kSIa+lFaDSMDNkUmeE3z6tzQn+ZTAIDLBc6somtvBDUs1Imdm\nrJ49k9/rt5tbNyWEOvApkz7FhtYDKl0GmYQby3A9D6K4yKT4ZxeD3LJvjTOHcOkkyIBPqmScdmtP\nr1RY4W+XH6EdkTabCw3Jbqf51k+Pwvrp0dLvVYXIoDT/amLc3Dpphj05B8i9F20MPodz/K5VE/C1\n751wyjao4kPodpxuZN30E6FbZADQgR8Kym4ZONvkvEyU0mteKLuisty6fw3cun9hgksk+UFCFpXP\nvteNVs3qyN5U2jqemwvlvLPK0+VuNhJxsK2UTZ8QKsNSHuGOPTs5XIWZ8TrsW7cUfvdvviLWr8+Y\nRMvTLVksM99CI6WcNSB23lssFbgIxbgw9l4GYfs1sMakIuMHQGZF55b0TiSmPe88tA6ObVkGr33f\nZ7uWby+lIijDKHQRNBut/pQL5dCGpfDxR74NE3lYWDMp2+XhBoN7L9oE1SQR4cq1ADKpSAnQ94T0\nUBIlcCZ5oNb0b4kzyUHGCFFRYt1auGHRVawUbJoZg1+9Yy9cun02f2bwV5MQZ5LPKOc7SaKTOtan\nTsNzGncm1GGZT1iMQIhn7y12s+0NMonMod1yc1MqGCUuhmS24zJI1xb4pA5DXPdz4y+5sNlubso5\n6GhHpsfqDmpXkmdOZ+vOrlWT8IHPPZaXp/18+yXvfOEBHfpdkl59Qmy6/azDIpoE7HNFiDN6t31k\nUjamiqTTOeb9DxyDz3z1+50lEpBKomCu4c4N3Vibk8Q+ZFJKFdY9NdJZ5elyT4/1ktAo64L6mBb2\nU/SN89ctgXffcwg+8LlvZveE5OZ9yKQubstxv7Bt+VjX0mxH8PsXmoDb5QqLfO0M0F17Jf2omUGq\n/YE1JoVqeSGteEc2T8PhTVMDY0yqRp7G+8iFey0vu2QLHN2yDPatW8rKk/2Pk6I5/c3+r1USuO/4\nJjHNkJubTaQql4m/xg1ZSkAm+dBIFjJJ6Le+U+V2Tpv54aRv00nD0yNyLQYuvVglpJx7jUn5//wu\nVXg0MokhD/g7g7Qg+CTGRZLeHUTBMdVNJAd1R+uem1sYmYTFnxiqwJOn5mF6tN6VfO08hLkz/78b\n6+//9fz98PXvn2jr3X7qvzzwA4Dr+ldja1Mv5ZHHngQAgJ0rJ/S1QdgQFPGh9IOA2/RfYZPfxyos\nWmt1BN4ybm7tzj0eXYVLp+2zc9UE7Fw1Ufxgm5KiMQkN3vn1bkzJaW4Y8hlDxAiLXmhS5+WhEoVM\nIn8XBapYWnA4j7QZJjKqmxYik5awaHkGDd55JWyZHYP33HcYzl+3pPjhHsqiQes6vxf/mjAoMgio\noX7IAHMmBZTZbg/ckuNuEJQ3FINMCj+nTyz6/G1JoixDEifpw0lRIkL1Sb0a982hb6VtLCGTTs3b\nxiR64mNP5OZvCYbtUwLpJlVCwkgTnGMQcE4r3LwOb5yGV16xFR6+ZY9YjkGQsQBPgx+ZJPu5Scik\nCuNEKeMSNihSZrMwaBwtV5yzHFZODvUEfUkRRN2qF6WggDMpu7d+ehT+9qevgL1ru69Qm7XWvdiN\n9feqXSvgngs3dpxOr6WmkUnufFxLE1BKkfmh9+V55nTm1n9ODzfmCyE9MyZZ7ebPo5+ugkVRK7E/\nFUVok5DlZaXIcN1p+v2SqmcMdgWZpATOJHooKQZ6yYwpt+xbDf/5+fvtd7soI9VivIBSxoBUScJm\nhqlRP3oQwHDI6WVPSKzRbMFLLt4Mn3njVdb1G3L08ORIOI9YObJ5etEcgnbTUNaOdKqT7l59Zq0n\n3ZAfuWA9rJocgpvOL0a9dyqDYK8aWGSSNBYWGmY/iCJxPkjCPHkWTtgeH4tdFU6IfVITwjlLEsRe\nkJsiZ1LIzc1z2tcSCbjN3/vXG6NaKEIJgDz5OG5uzn35nVdesU1IbTDk4Vv2wFU7V3jv+2Dd5uRS\nidcBjJK9dXYMLtqyDM5ZMQ4AcUa6QZMyLveDFor8v7zwAAAA3P6Ov+p62jZnUnfqJVEqjEwify8b\n6z4qCUBeazlnYd9lAbrdxFAVnndoHRzdMq2vYf/X0R7b5KtpR371jvPgY498G1ZNxoU1HxTp1ZQi\npSt1334eEBYik5CAu4T+0r4xSUGaZK5JYQLutpLvm6QedGA3yp0k2eGdPReSvIU8EqWglibwK7ef\nB98gCMxu97MYNzcFBOlfwJk0VYBy5QF9fElJ9f6aq7bDSy/ZrF3UzgjJv3Oh3dxcnTT+3T97xTFY\nTQI6nJVM1k2PwF++/vKe5jFIqvQZhUzCkVvA79a2nIlGqhABN5V+hsaNEQOUyv6oluClwOheRVGn\nYjd/HBWVGZO4m5ucFr0aUmI3zYzCH7z4sD71j91M8nKFfp+J0Ndj22ba5EySCROpCwRuGpeO1uB3\n7r0AZieyDZxbr4MvZQwh3Y7m1i/pDTKp+8akjDMphEzqSjZRIrkELZTszxGs/TTeJomCX7hlD+xa\nNWmukVN+ALo29b5c66dH4QVHNgwUOjpG+mlMEp/rTfaiFHEm4fxaxkA0VGkPoZEoFaVbLfb+VvHM\n7d3QeTKPNcqZZOcj6c4pORCoFBwMdiIh3UfnqUw9ZMgkfymmOAE32G2vXTDRmFSCpiFJ1JllSLJk\nod3cODIpvqeds3LiDG6Xs9ItGVC1v5g8+azEiVlkw5WnfaAXWR1jcSoldrAhziQr7ZDyRP6WIKQn\n5xp5ubJ71N5E65r+LRFwZ+8qqFdS7ZLI84xFjRRFc1tsbdsNKfqkQhJTdpvunUMkyFQWmyG2HSlj\nIBtUJFYvorlRVEoJT9ygKAi79erw1z1UYA0XBLmGaKWe5RqW33rhAfjfL78oagPVS8HhjuWodiGa\n2w+79GNOQZJ+iWS4n1N4ETIJ56dYY9J1e1a07aai1OJ3YYsRHlyh1UWkCLq5+ezqElI3c1XO9VAP\nar2vEolMGh+qOP2BHiigO2FRMIszoEtFCUfwLhZk0lkZMFlEh3Y+GVhjkjRLmUu9qfgzcUCaBS38\nnIGtLmwl4AaJR3OrVrBcxeWLNiYFb7p3W+QWIpOkvOibFjLJ020T5ZbF5kwSyiIk5rq5hZFKZ4IU\nfZLP0OPzcacnkL79/BlYjaWUv0HdfCQFCnA7Qo3c3XL/Swo2eH3pf6H1d4H0nrF6BfasmSx+sMfC\nozx2I5rbD7v0quroMvmKy7fC537ualhSgL7otRShiGIDBaBb/F0XrG+7/BkyafA7rna/KuCNbEey\nyGw0aAeL5uYh4JaQSQuhgylQJpBNAWdSkihYKowPFB6QwPc5ix3J1m1ZaFPAmUi98MMgC73fLiMD\ny5kk6dI4QQ2AEW/RSDWNU0xwEV7oqAQo2scb3dzaQCYVGhp8rmkR72EfHKqm8PTphhdJRP/2uWcm\nyj0tCrWXbwJyjB9Omt4kB1aK+rXPXdDn406byIdMOhMJuB3lL/BNiVLw4QcvhrlG0//QIpSUzSld\nSdM6de5Ouip3kfizVxyDz37NDafdT1uSxRPSB0TUIAgPs20ipi5YkQZe+rH5SRIFo3VZJe7n2lgv\nIODGshQhHX/y2h1w3/FNItIqVooM14MiPOIqSjf6VZJkh0zaNV750ecoKXFVtpBJHZcmXmqVBE7P\nNwFIedMCZBJARsL9nadOZT9a9vchYrbIk+GHxZiBX9ls2Yfg/S/HmaeTnpXFJQNrTAqGJu5Rnmei\nkYoT5vkE17tmrwip2pThWgqJMkSDMZNkPT/5K1zQArd96CKebjEyycImiXlJ5QxGWIlcwHkSZ+Jp\nUdEX+fqARsCx2zNjdfjWk5ki5UUmReYxSFJmP5EogM0zY70rTI+kF5xJdJx2a1OGG7xzVk7AOStd\n95V+HKoYl7aWe21xLRF9F2xmHe1RiPh2VsrJQk+h/VwbCzmTIpFJSqmOCfgzsv/+cX71Svjc7lvf\n20pbqcyY5M0b4Fdu32u5L1LeO0uX61IVv+vuA/DYE6eCz9TT3JjUMtlmZQoXIoRM0ofTGuUrp3UG\n2CejBMcM7psWi5vbD0n1nzEyCCrVwLq5ycik3uR1Jg88Dkv1CS58C21L4hHbn713Fbz3/iMwMRxP\nEGcMPOHnYtpdqjd6Dcm+fZxJVJot+V6i3Hx80eFQpGbim1me1xm5wEf2ay5mQ2zff99Lj5J3I5FJ\n4SIMhJQhax/Uk+winoe20iQuIt2K6qWUsvjTnDwRRdrDufrBq7bD7Hgd9qw2bmW9PswZFOFubmWC\nQ5wVWXplyIhNtl9tV68khd9qb/x7K6+7ZgfccXCtle8gijHYxK9jsaJyziQgaGaaaqoU3LJvDVy3\nZ6W+liiXrLpb5QEAuGzHcnjeoXXBZxABd6phkPMxyKTpMWJMYs9WWHRoX1ojHgTgmSrGBXJhpCj4\nzlk5K53KwI5oadJFg8KKRRYW9wOvPA4jESE6F0JqaSwyCY1JC7tV4NkPVVM4sGEK/uWbTwJA3GRd\ni+RM8rq5gVlwJfc6EZnkMf7Q86xWqyWWPxEibATd3CKRSfyxQT559EmRcubjsaH8V1TWTo3AjhXj\n8PlvPimG/JXeORMWbhqhar7ZgjWBULGDSjiuN2ddLD6dH975woNdSfOlF28O3sfP6OVMfXDDFHzq\np6+wrhlk0g+3OclxcztLwD3w0q85vIh8G8B2Seq13H5wLfz557/V83x6LWnSO4NuojK91KCdbIOM\nGM0tMYivooPBXsnv3nsYfv9vvwIzY3XN8ZmqYnMWRybR59Glt6hrLh354YgOpqtBGxoXZhXg2U7+\nkNT/WemfDK4xiQyOj776EqikCtYsHYH/8Lzz4Ypzli9cwQTZvmJ8oYvgFXOSEH4OlanGQkOTcnHm\n5BIbmFg3t9BtHUpVsCjQuixyc6Pi+wKJM8ki4HZO2+TqKOLyGVAbQFCK1m6v4SOvwFCdpB50CFcY\nzgBbkv6Gl1y8Ge47timojHSLaLrf0osgA7hRuPG8VbBx2WhX0rx0x2zwvo7m1nejTp5vn3NdbIL9\nX7u5oUFxQMfFWemfIXCogC8JwHSjfh9SSNn9+asvgUcee7Kv5WhHKtrI0f06S5PczY2g5ukaIq2H\niTIE3GmEbtgL2b5iHH72hl3WtQyZFC7FFOXgYpN91UEmyWkt7YDHaxBloddE2gq/eOseuG3fmgUr\ny1mJl0GiDjgjjEkbiJJ+Qx7etRdyJhKLSlBbSXDfvODIpII2iOJMqpaLYBcSMVIHgfhyQsJQIZvN\nlniLZoHVT6NEte3mRpaY3asn4MGrtovlGmRpVznbs2YJAABctGXGTVO5SuCZLproPk0KT7UGFYmV\nRp6qlhHcMPSzRoxLcn/n6kFSfHopWA8amVQ5i0xarBLbVxcTMskQcPenTCaCrisbl412zUjeS+EE\n3N2co9DNzUIzk8qS2kkpst7krmUtD81BP0Qjj1MV5uMEZkxigofTRX1zKsC7dCYJNqch4F6ocpic\n7zgYdn88K2elHRlgzqT+Dcsz0f0HpRpJrmiQST0vUqTY5S2jG0hoITEHz22lzD3pEUU23oYsk9z3\n5OcncHSxEqEF39eWHEhDH/uTHz8G25YvXgRdu9LuPHHe2iXwzz93NVyze4WQZvZ/kdLVaRkWk6Dt\nMob3p0RgxUUlJgJN99rLhIXvXx8wyKS+ZQkAZzmTUPScj5xJPXSxOSu9kRcf32T9nmv2R/EpIt8G\n6P96ciYYh7VRn1VdN6oyVVn0XoNMshMdE/iB0kRZa6mvfP0SagAvMmheu3ulcXNn5a0yDlbf54QM\nUmeSYF/QxqQFbt+zclZ6JQOq9p895euWGGRS+LlkgU67feI19ET0DORM6mSDR9/EcMKogGJd1tNE\nP0jdqbwRxFoB4xQn0AuEk/V91aCFrP+l286F376nM56ZTr5RUgJpmrHcQIu9nmPEIJMi0HoD+sG9\nIOCONTh2UxZqrtbz6SJZIxZKsB+lJQywZ2VhxDdV/dR151i/nzw534fSxHImZf8v2PgeQDFze/e/\nIUkAGq2WFSEOc3ng8q3wwgs3uO8oZQXwMC7WCyOYb5ooHRnZJysmh+DBq7aJ97TrXoFxbMkPGWeP\nNjQuFGfSguR6VjoVc0C3+HWqgXVzOxNO+xeDVCPd3HBP1FxgziSf/lRGrzKcSeHnYvqYUgpqlQQe\nffh6571qJdHH9BZnkidZH8eJRIpIN6mim5uQVsjNbTHK7QfWdpxGL74R0wwE1LLkTJirDBpr8Z2c\nd0uKFOCO0uxekoXSDwLukCx+tae3ot2QtOtIfnixUAU6Kx3Lkyfn+pLPUCWegLtftqQzwTZc6SkB\nN+NMImd/25aPwcSQazhRytbhKomCUz0qX4wxEzHeAAAgAElEQVTQaG7DUa6WckGr+UHtuqkRuGzH\nLOzN6QK4+A7qzjRRC7wWowyyIfisDIYM7Iju59i4atdy2P+ppfCKy7dGv7NsrA5X71pcROCS4CKL\n69pn3nilOPGgYrxI+Le9EsWZ1KmbW0E+eK+WJtqinAaQRChNj8+8ZPQKoWJ8ZRs0ZFInglHHerGD\n05DwCMPK667Z8f+3d+9R0qV1fei/T3X3e537hWEuDAM4OMP98jqACA4yMwyoS42KRxMdjR4i8TYG\njyBqMMIyrkSNYZnjgRiUkBVP9JgjRqMcJEEjJieMHPGELAOeiAKiMlyiyGWYt5/zR9Wuru63qnp3\nVVftrq7PZ62Z7qraVfW8VU/v/ezf/j2/J3etwH5gP8Opm22mYaxoJffeAq5eDzO5lviRbCz5ZLPx\n2OsuyfMee02+887xV63XRdOPmp8nhlM/VvPvguVlJp1sUYB7GCxe0h9418uaH4a9FwoO85PrB5N2\nvo+SndV3Jx1LNsru2kQ7x8yOMleGY5p2waQy4YNspvSeObGZ13395KzytdsXdnzetKJDMlbICgeT\nlvfXccmprfzCiz/3QM+57/vu2H+jI2BrT02PyyYUxivDYNLRiCbt/fYPMrA6sbk7gDb5PdpkJo27\nrznxLsMTulaZSakTp7ntfc7uFUDa/S3sDSatagZJGxuDYFKbf+K9d9ycp9x4eevXPkgB7hffPn0Z\n91UxzLY7xqOS4fd5qJlJTVbK8j63rqa5bW308pqvPbfU9zyKenv2D8OsiM5axCRXX3wyZ09s5Hte\ncMvU7f7ik8vJTPqcm67Yd5vecCy26NYcH8NaPoO/wuaC4mH8TfZKP2N/tAD3fkODOx5zTa677PTw\ndvc1k3b2VW1WFNyYMJ5tM6X3klMre9o5s+3abiy6KEd9FgLjrdIp2vr9VbPLVtuaSUckmLTfu7f5\n29vslfTKvDWTJj+3+Sy3NnrD9u4uwD3+uZM+2nEFuHdlOu15sKTkKTdenv/wnvsnPqe/3fE1TBtv\nse29dxwsk6J5zWWtpnMUNIPv/eoprLJFrua2TF0V4Kav+cqboN7mnqK0HB0nNzfyrh+8e9/tnnPL\nQxbajv/4PV+QTz5wPo+8+qJ9tz0qY7FVsjcz6Q3f+LS88Xc/kKsvPnkor71rmtvIY5P+5l969+7g\nZRfTofcqpb/POtXiGD8pkWqzxdz/SResj7Oa7r9bWCTBpDXX7Pz3y1JpjhHnj2rNpAO8RiklJzc3\n9s9MmjTNbbTC4hjNZ3li5MC6sTuaNFZ/adhxr3dh4GtaIKOUfrbN8x//0HzzG34n7/3wJwbPuXC7\n42qYnbGARXhGU8LXxXWXnc5rvvap+fxHX911UxZm54Tj8L7XRdRh2v89+z+dbHZjb2bSMPv3WIfv\nj693v+r5w2zmRbn20tP7b7THsoZiw+lbK9x9d8o59P8Rj7jq7IEvIk1SSsn57TryOe1kkrf9yBZx\n7Dmokv7FjwNNc9ujTeby5WtUfHu0WH6XMwFW+W+X1bgwuLKruSXJE2+4ND/6lU/suhkrbXN4NX76\n3qY5OT9/RHr1pINZ24Pxya3eoQQDxr1C87InNnu7BhjTnpNMrtg/+t00r7dfxkMpJbc89JJdV4ou\nrJl0fI8wj7zqbP+XBfwTm8+xi6yTLj3vsQ9ttdrQqlrIam4bh/+a+1l2gV52Gy1mm+wEk8SSVtOi\nA0kHtZN5uJw/8GfdfHWe89lX5/u+8DFLeb9FWGRQf6P0yxmM1pY6aOC4CTx3OaQopaRXys7+aoph\nO2syumNr89xL1ygzqekHk1ZqXnY7WC2rdI620plJb/zWz+u6CStvp2bS9O26Kuo6yd7mNkGTNkuX\nJ/2soXmuFEx7ZrMDOLHRGwbfRps1aQexvefA3OjtO81t/yl3e59z3L3u6z8nb3/vR3Pp6cO/CtZ8\niqtaaJrxhsszH+o0t8WtIjTJxpJPNtmtqct/wTS3rhrEsTKsfbykP+/TJzby099w23LebEE2FziN\nrNfrX2QdXc2t0Xa/v7GnplMXeqX9BbJJY8k2NZMuW8CYjOlWKCbBilrpYBLz2xzWTNonM2nweNfT\n3CZNaHvhuRvyvo98It/ecsW9k1u9faO+bQJG44zWTHrwM+f797VazW18kb7+NLe97z+tbaPPLWN/\nP+6uvOhk7n7cQxfy2s3HuG6ZScfdTgLJ4U9zW6Zh5sLS35lkdJpb//ZWBwFFjq9ml2Iaa3uLrFvW\nX81tpAB3LlwwZT8bC7iQcVAlZRjU2s9wLFmS0SNNm8yky9Zwmtve35dtncb+x9Eq7OkFk9Zcs/Pf\nb5XzrlYImmTvvvHk5kZe/oJbWz+/Tc2kie+9qx1jMomazKTNXj7RBJMmrH4x+nFO+mh7pUw9wZ32\nzxg9mXVAORzNd+HzPF4WMaDfu4rQMvTUTOrU3mlum0cg64DjQ7D44Iarai7gmN1rprmNq8DddqXd\no3Bhquxepe3ik5NPDyd9jG0usK1jAe6k2/2/oepqasaPq7CKsmDSMfUr3/55uWjKwaCx1Tozqf/z\nuJyfnD2x0eoqyiTTPq3hMuoTCnBPzSqa8nrJ+M9/3Gpu4953naa5LdIwM6nlVTxWw8YCMkg6KcB9\nxKYkr5udVQF3HwcM6DkUMpMObKHT3MrujP1ZslE2OzhO7DU6ze0/fPdzcnbK+cNwTLq3ZlKL+mLr\nNM1thrjiQjj0rKave8ZNuf/jD+Sbb39U103Zl2DSMfXY6y5ttd1myys2R2Wa22GNn37wSx63bzHh\nNgf2cZs0zzu52Rs2ePdibgfbtfd6F77R1EylXYOZ0WDSgd6WCZqPVGbS8XLRqc2c3Oztujo7ry5q\nJjVXuZ1qdqM5Ru0U4O7+RJHj40ufdH1e8xv/PXc9ZjHTuI+jRa6W1usNprmNJCYd9H2G9fq6zF5J\nGR47HnbFmanbTrowubXfFIckl59dn2DSqC7LIjj2rKZTWwebcdMlwaQ1t5OZNH27ozLNbTgvfc6d\n4xMfdtnMzy1lv5pFOycRTXsnTXMb99p7bZTpQ4xpj91xy0Pyzvd97II2MLvm21Az6Xj5nz7nYXn6\nI6/YtQLivHYG3Uuc5qYAd6eaRReGBbibgKLrwxyCW6+9JO/94S/suhkrZbGZSSXb23W4Gm9vZLzW\n9v0WWdOprVLaj2kmTnPbJ1v7jluvWasg6O6LuV0Gkxx7WCy5CmuulJKNXpkYaLjloRfni55wraKP\ne0zbN48W4G4+rrlWjtuvUPiex0dvfctzPmv4u2luh6O5+ObzPF7OntxsndHZVtvVJQ/TcZuSvGq2\nt5sVPGUmwVHQXCBYxAW1jVKyXZvVePe/2DjpNZrndqU3OBdou22SZM+/ddLx7kXPfmSe+VlX5qfu\nOTd1+txxM/ppzFNW4zDbAYsw1191KeWKJP8qyU1J3pvkhbXWj47Z7p4k3ze4+apa6+tLKWeS/HyS\nRyU5n+Tf1FpfNk97mM1mr0zMTPq1e5+dJPnf//MfJzkK09z677+cq7z7v8f41df6d57YnFQzacoU\ntTHvOW41t+b+cV/H6Ov3eiVnTmzkEw+cl5l0SJrvSDCJ/XRSM+mIZJGuq+YYuTPNzTU76NIiaxL1\nev1sxJ1pbu3GeqOGx4lOp7m1H9Psrpm0Y3PCNLdVmaqzSN1OczNWZbHmHeW8LMlbaq03J3nL4PYu\ng4DTK5I8LcltSV5RSrl88PCP1FpvSfLkJM8spTx/zvYwg62N3v41k3pNzaRltKiFTtOBp6+utisz\naXC03VXHaOprX3jfyc2dYuGjx+62J6rbe6ZdMJ/m8xZMYj87U5yWpxnodxz3X1vDaW6D72FnCov9\nBXRhkcfqUkpqrbvGeged5tbFRYe9brjiTB52+fRaSY1J8fE2BbjXye6sre4+G0NVFm3efMMvSXL7\n4PfXJ3lrkpfu2eZ5Sd5ca/1IkpRS3pzk7lrrzyb590lSa32glPKOJDfM2R5msLUxOTOp8fRHXJkk\n+fKnXL+EFh19bWomndzsZXsQfGu7mts43/uFt164YltpTlYuPGPc+/LDgrBOZg5F8/0KJrGfLmph\nqJnUreE0t8G5w3A1t64aBGtukZlJzTS30d3tQQPHO5lJ3fnV73hW621H/327pnIZE03U5eq/6vWx\naPMGk66ptX5w8PufJrlmzDbXJ3nfyO33D+4bKqVcluSLk/zjSW9USnlRkhclyY033jhHk9lrc6O3\n7xSoG688cySKPi7z9GjWgcdoZlJjY9fBd8o0tzEPPe768XVcdlYAmW5Yt8lFo0PRfN6Cc+yni9T2\n5sRELKkbTWZS8z0chWW/YZ01NZMWsppb2V3+YTQzqa2jkJl0EKM1k0YPM4e5eMVxcHQKcHf21qyJ\nfYNJpZRfTzKu/P73jt6otdZSyoGHr6WUzSQ/m+TVtdb/Pmm7Wutrk7w2Sc6dO2eYfIi2phTgPqqO\nRsWk8UZrJu2sPjd7ZtKopz+ynyH2jEddmZ9+23vHvuDe12/SrwU/DodpbrTVRS2MYQHupb0jo5rM\npOY40Ez9sLc4uH92z7l84GOf7LoZrLgmoLuIQ3avV7Jd6656nhNKCk20MbzStxp7ieHnuLdmUofZ\nN0fdlqu5HGP7BpNqrXdMeqyU8mellGtrrR8spVyb5M/HbPaB7EyFS/pT2d46cvu1Sd5Ta/3xVi3m\n0G1u9ESu9zjR+grLuILZO4VX656r1OOfMfpq07+I2x5xRf7bq+7Oyc2NiQOjvVffhtPcBD8OxTAz\nyefJPoZTnJY5zU0B7k5dUIC7t7isiOPuubeOS3aHg1lkUL9XSra3Rwpwz/AWTQxmVYYUky4+tx83\nr58uA229Fct8Y/XM+5f/S0nuGfx+T5I3jtnmTUnuKqVcPii8fdfgvpRSXpXk0iT3ztkO5vCEGy7N\nLQ+9uOtmtLJzwF7cXvFdf+95eecr7pq+6trUx/o/R5dJHR0kjD51loDEyc2NXc/dd5rb8H0dSQ7D\nsLDuqoz86EwXtTCaDETBpG6cb6YV7y3A3VWDmNklp9ZnGfPjbJG16zZ6g5pJg9ujf+1t69ZtrFjA\neTSYNNpiY6ILNR9Vl1MAfSss2rxHyh9O8nOllG9M8kdJXpgkpZRzSb651vpNtdaPlFJemeTtg+f8\n4OC+G9KfKvf7Sd4x2In+RK31p+ZsEwf0E1/zlK6b0NruA/ZinD25/5/FtPdvDrQnR1a22L2S2s7v\nj73ukjzhhkvze+//H/u/8IT32W/8MS47itk1n7fV8djPTr2cZU5zUzOpSw+5+GSS5MYr+isjOcFa\nTb/6Hc/KVRed7LoZHIKbH3JxHnHV2Vx6euvQX7uUfp200QudB5/mNnjuobduMSbN2DLGnKzL48BI\niStYiLmCSbXWDyd57pj770vyTSO3X5fkdXu2eX/0bVbcuHPEncyk3k7x6wk1k0opecldn517Xvef\n+7cP8N5tgxnNgGZSzaQrzp44wLvSfEtOEtlPF4PrZqAvmNSNL3rCtTl7ciO3P/ohSfr7+K2NsvQp\nBm/8lmcu5OR5Xdx67SVdN4FD8oxHXZl//123L+S1e6Wk1jqsTTnLLn9lC3DvsSqZVctU0h+Ddzle\n3Lnw7PthMeTwslKWudz11NpGUx7cXYD7wuLXe5866+69ec396gBMW83tV77983LNJadmbMF6asYE\nMpPYTxep7cPMJCW4O1FKyRfcsrvWz2avl2VfO3viwy5b6vvBOtoo/Wlu26OZSYPH2g5Xh9PcVuT6\n+qSLo0y2dQSmufmqWBTBJFZS1wewaQf9sZlJvdHHy9jtxz02zUGvZo3LTHrsdZe2fj/6hnPgBZPY\nRxfLwm8MC3Av7z2ZbrODzCRg8XplUHR/JHK087fesmZSMw1pRfYR49qpvth4pZSk1m5Xulux/sXq\nUXof5jBu37w7M2n3feOeM+vVqIOuNGo+++Fovq9Jqd7QWOQqQpMM63WY53ZknNjouSoMx1BvJHi/\nd0hw0MykVTH672p+/9V7n91NY464pktsdvgd91rOYoBZrdYeDJZoWqxg+jS3/s/RZVJHAzlTX7dt\n4zJ6gJjuRc9+5OB9HUgOQ9vMpNEC7KynLlLbd1ZzW/pbM4HMJDiemnHY+VpHphM1U43bGRbgXuF9\nxKSanPR1WoC7s3dmXchLZKUMV8w4IrvHccfPXZlJ9cKijHufM+sxeFgzaZ/nv/wFt+blL7h1tjfh\nAs33Oy3T6/9++XMFkxj+3XcxzY2jY7PXOzLHLODwNPvb89t1eMHuoPv7Yc2kFQnIlCnjWXYbXnzs\ncJrbrP0S2hJMghlML87df3RrY9I0tz01k3Y9t30bFIDuSOkHCaYN/BQ1J+n3kc3ecsMIq3JCsk66\nWM0NWLzm7/r8dr1gP99+mtvgtQ6tVRw1R6IAtw7Ggrh0zkq5946bc8XZE3nCwxZfOHreaW5bG2WY\n57yrvs6U5dwOsq9vu5obh6tE9sc4p7Z6ufGKM10348jZ6C03kKBvHj3XX35agBmOoeE0t+063M8P\n69a1nOi2OcxMOvTmLY3VQ8drxuddTnNTM4lFk5nESjl30xV5x/ff2XUzhsbtnMcV4N5VM6nFa7R6\n750J+ixRrxQn7GO86+/drSuO8d1335Lbbrpiae+nax49P/31t/le4BjaGA0mZfdJe9vMpFU+2V/F\nNi/VcJpbh7kbviIWTDAJZjJ57zxagHunZlIZeXzPNLdd88/b7/UFNLpRimKT4+iP433j5z1iqe9n\nlcGj54T6aXAsDae51Toyn+hgr9HU07HrPr46LcA9eGtDNBbFCAcmmHbFZfoUuAszk0ZXBb2gAPeM\n7dtZdpxlMs2No0zfBFiOYQHu82NqJrV8jWFm0orsuk9tbSRJbrxyZ1p72yysddN8pZ0W4G5+rkoH\nY+UIJsEcxu2bm/tGC+6NZrJMDVId4L13BiAOEMtUTHPjCJOZBLAczf72we06Ml2tr7aMsGwOLwyu\nxr77+stO559+3bm8+qufvDIBsK51WYBbnI9FM80NZjDt+LmrZtJgLz4a8LkgM2nGo7GARjdK2VnK\nF44auwWA5WhW1T2/vT1SgPtgO+HmNVYpMHPnY65JIiNpP8132uU0t+F5SGct4LhzRgSTtNjzjtuk\nN5KZ1KxwMbUA9+gdB9jbNy/pALFcJSVd1lKEaWQqAixHMw47P3vJpJGVeVeXw850XQaThqlJviMW\nRGYSzGDaCVuTmXRyJDOpNyVgtPuh9nv7VZtnf1xcf9mp3HD5mf03BACOrWYctr1dh+PCZkzWNmtn\npwD36g7mZCiNtz34XLpcze2S05v5G0+/MS8897DO2sDx5vo6TDDtsD71scGAYGtjNJg0uWbSrAMI\nKwR14947Hp2f+1vP6LoZMNVfe8r1XTcB4FjbGNZM2p458WNvraVV8lWf0w9QXHp6q+OWHE0Pnt9O\n0nEB7lLyqi99fJ5ww2WdtYHjTWYSTNAmyDNum62Nkq2NyUWa9z7l8jNbEx+b5uQgmLTCF7NWUk9R\nGo64//aqu7OlrhfAQjXjr/PbGUaDhgW4W5Y+3lzBmkmNe++4Od/ynM9ycXOCJjPJ8ZjjTDAJZjDt\noP/Vt92Yx19/6cTt9z716otPztSGk5sbg9dbwREIsDDNvgGAxdkYLcA9uK+5yNh26tfVF5/M2RMb\nObW1evvtUkpObBqD7qfLzCRYNMEkmOBJU1JCpwWTrrvsdK677HSSnaVhd6/mtvvJF53czKmtXj71\nmYOlSZ/c6l/peHDbZHUAgGVqpqidrxeO7doGk774idflWTdftZLBJNrptAA3LJi8O5jg0jNb+Y7n\n3jzXa4wbS+wNRJVSZspOarIPPv3g+RlaBgDArHamuW0Pf9+Z5tbORq/kyotmy1BnNXRZgBsWTe+G\nKSZlIB10atmUxdySJFcPBhKz1Ez69Ge2D9QWAADmszPNre6M7SShsIfMJI4zwSSYw37BnybNeVfN\npDHPecjFp/qPHWAU0kxz+/SDgkkAAMvUTHPb3t6Z5taM42rbeW4ce1sykzjG9G6YRcuYz1MffnmS\n5PSuufAXPnmeaW6f+oxpbgAAy9QEkx7c3k6TfNJcMBRKojFpdWc4DhTghikmXVhqe1j40Rc+MX/7\nOY/KZWdO7Dx3zJObYNJnzrfPMjolMwkAoBO9Yc2kmgtGhqJJDGxZzY1jTGYSzGG/aW6ntjby2Osu\n3f2cMds1waT7/+qB1u99YqMJJslMAgBYpibj5MHtOqYAt2gSfZs9p9scX3o3zGDvErDzPrcpwH3/\nX3669euc3GqmuclMAgBYpmaa22gB7jmGhxxTmzKTOMYEk2AG8xwWpmUmfejj7YNJpzZlJgEAdKEJ\nHG3XekEQSf1tGgpwc5zp3bBk02omfegAmUkPv/JskuRRV190KO0CAKCdXdPcsmc1t85axVGjADfH\nmQLcMIN50pjLmNykqy46+Gputz3iivzCiz83T3rYZbM3BgCAA2umuW2P1kwSN2APBbg5zgSTYA7j\nAkP7PmfMU04Mpqxde+mpA73WUx9++YHfHwCA+TTBpAdHaiY1THOjoQA3x5lgEsxgliDSfn7t3mfl\nyrMHz1ACAGC5mtlL/cykwTS3wX1Wc6OhADfHmWASzGCuaW4TnnvLQy+Z/UUBAFia0ZpJO1OZBjWT\nxJIYUICb40zvhjnMElRaRFYTAADL02Qjja7mpmYSeynAzXEmmAQzmOewIN0VAGC1NTGCB7frsH7S\niUEWigACjS01kzjGTHODWcwxRji9tXF47QAAYOmagNH58zuZSS+569E5sdnLlz/lhg5bxlHiIjLH\nmWASzGGWw8PZk/7sAABWWZONdL7urOZ28amtvPwFt3bXKI4cwSSOM3l3MMWk+onz1D06c0JmEgDA\nKmuCSQ+OrOYGe22a5sYxpnfDHGYZPJzc9GcHALDKmhjB9na1tAoTyUziOHNWCzOY5wKUq1cAAKtt\nNDNJNIlJFODmONO7YQbGDAAA66s3cnHQuJBJZCZxnAkmwRwcHgAA1k9vZBAo65xJNnv6BseXYBLM\nwKABAGB9bfRkJrE/5wwcZ4JJMAPHBQCA9bVrmptxIbCGNrtuAKy0GQcPX/O0G7O9XQ+3LQAALMWp\nrY3h70VuErCGBJNgBvMOGX7oyx5/KO0AAGD5zpwYCSaJJQFryDQ3mIOxAwDA+jk9mpkkmgSsIcEk\nmIExAwDA+ur1Sk5t9U+lDAuBdSSYBDMxbAAAWGdnTvQrhrjICKwjwSSYg7RmAID11Ex1MxwE1pFg\nEszAoAEAYL01Rbit5gasI8EkmIEhAwDAehsGkwwMgTUkmATT1Dr1YWMHAID1dHqYmQSwfgSTYAZq\nJQEArLemALfUJGAdCSbBHIwdAADWk8wkYJ0JJsEMDBoAANbbmcFqbj0DQ2ANCSbBDGQkAQCst50C\n3AaGwPoRTII5WAoWAGA9nR7UTDIaBNaRYBLMoAki1Uxf7Q0AgOOpyUx6cNt4EFg/gkkwA9nMAADr\nrQkmfeoz5ztuCcDyCSbBHExzAwBYT6cFk5ji1msv6boJsFCbXTcAOBxf+dQb8s73f6zrZgAArIUm\nM+mTgkns8fuvvDsblvnjmBNMgjkcpelu//Arn9h1EwAA1sbprf6p1CcfEExit1NbG103ARbONDeY\nwVEKIgEAsHw7NZO2O24JwPIJJsEM1EoCAFhvTTDpgfOCScD6EUyCKSz0CgDAOE0BboB1JJgEAABw\nQGdOKD8LrC/BJJhBlbMEALDWzshMAtaYYBLMoajEDQCwlkxzA9aZYBJMMSlUVCUmAQCstTOWfwfW\n2FzBpFLKFaWUN5dS3jP4efmE7e4ZbPOeUso9Yx7/pVLKf5mnLbAI+8WM5CUBAKynzQ3X5YH1Ne8e\n8GVJ3lJrvTnJWwa3dymlXJHkFUmeluS2JK8YDTqVUv5ako/P2Q4AAAAAlmDeYNKXJHn94PfXJ/nS\nMds8L8mba60fqbV+NMmbk9ydJKWUi5L8nSSvmrMdAAAAACzBvMGka2qtHxz8/qdJrhmzzfVJ3jdy\n+/2D+5LklUl+NMkn5mwHdEL9bQAAANbN5n4blFJ+PclDxzz0vaM3aq21lNK6LHEp5UlJHlVr/c5S\nyk0ttn9RkhclyY033tj2bQAAABbixivO5JFXn+26GQBLt28wqdZ6x6THSil/Vkq5ttb6wVLKtUn+\nfMxmH0hy+8jtG5K8Nckzkpwrpbx30I6HlFLeWmu9PWPUWl+b5LVJcu7cOWtp0SmruQEA8Jvf/Zyu\nmwDQiXmnuf1SkmZ1tnuSvHHMNm9Kclcp5fJB4e27kryp1vqTtdbraq03Jfm8JO+eFEiCo8o0NwAA\nANbNvMGkH05yZynlPUnuGNxOKeVcKeWnkqTW+pH0ayO9ffDfDw7ug5VVIzUJAACA9bTvNLdpaq0f\nTvLcMfffl+SbRm6/LsnrprzOe5M8bp62QBdKpCYBAACwXubNTAIAAABgjQgmwRSTCm0rwA0AAMC6\nEkyCOSjADQAAwLoRTIIpBIsAAABgN8EkmGLiNLflNgMAAACODMEkmIPEJQAAANaNYBLMoKrADQAA\nwJoSTIJ5KKoEAADAmhFMAgAAAKA1wSSYgUluAAAArCvBJAAAAABaE0yCGaiUBAAAwLoSTIIZmOYG\nAADAuhJMgjnIUAIAAGDdCCbBDKrUJAAAANaUYBIcwG+99DlJkluvvTjXX3Y6L3v+LR23CAAAAJZr\ns+sGwCo5tbWRJDlzYjNve9kXdNwaAAAAWD6ZSQAAAAC0JpgEAAAAQGuCSTBFze5K21ZvAwAAYN0J\nJgEAAADQmmASAAAAAK0JJgEAAADQmmASHEApqiYBAACw3gSTAAAAAGhNMAkAAACA1gSTAAAAAGhN\nMAmm2NrY/SeiYhIAAADrbrPrBsBR9ree/ah88oHz+bn73pePfuIzXTcHAAAAOiczCaY4fWIj3/OC\nW3Nqa6PrpgAAAMCRIJgELZjeBgAAAAEfls0AABBnSURBVH2CSdBCKWXws+OGAAAAQMcEk6AFQSQA\nAADoE0yCFgSTAAAAoE8wCVroiSYBAABAEsEkaKUMfwoqAQAAsN4Ek6CFIjMJAAAAkggmQStCSQAA\nANAnmAQtSEwCAACAPsEkaGE4zU1QCQAAgDUnmAQtiCEBAABAn2AStGCaGwAAAPQJJkELPdEkAAAA\nSCKYBAcipgQAAMC6E0yCFoooEgAAACQRTIJWemJJAAAAkEQwCVqRmAQAAAB9gknQQkkZ/AQAAID1\nJpgELchMAgAAgD7BJGhBAW4AAADoE0yCFoSSAAAAoE8wCVpoEpNkKAEAALDuBJOghZ4gEgAAACQR\nTIJWhJIAAACgTzAJWpCYBAAAAH2CSdBCGeQmiSkBAACw7gSToAWZSQAAANAnmAQtCCYBAABAn2AS\ntFBMcAMAAIAkgknQSpOZJEMJAACAdSeYBC30RJEAAAAgiWAStCKWBAAAAH2CSQAAAAC0JpgELTTT\n3BTiBgAAYN0JJkELprkBAABAn2AStCCWBAAAAH2CSdBCkZoEAAAASQSToJXeIJYkpgQAAMC6E0yC\nVkSRAAAAIJkzmFRKuaKU8uZSynsGPy+fsN09g23eU0q5Z+T+E6WU15ZS3l1K+f1SypfP0x5YFBlJ\nAAAA0DdvZtLLkryl1npzkrcMbu9SSrkiySuSPC3JbUleMRJ0+t4kf15rfXSSxyT5jTnbAwvRE0wC\nAACAJPMHk74kyesHv78+yZeO2eZ5Sd5ca/1IrfWjSd6c5O7BY38zyd9Pklrrdq31/jnbAwtRTHMD\nAACAJPMHk66ptX5w8PufJrlmzDbXJ3nfyO33J7m+lHLZ4PYrSynvKKX8fCll3POTJKWUF5VS7iul\n3PehD31ozmbDwZjmBgAAAH37BpNKKb9eSvkvY/77ktHtaq01ST3Ae28muSHJb9dan5LkPyb5kUkb\n11pfW2s9V2s9d/XVVx/gbWB+gkkAAADQt7nfBrXWOyY9Vkr5s1LKtbXWD5ZSrk3y52M2+0CS20du\n35DkrUk+nOQTSf714P6fT/KN7ZoNy1VEkwAAACDJ/NPcfilJszrbPUneOGabNyW5q5Ry+aDw9l1J\n3jTIZPo32Qk0PTfJf52zPbAQTShJTAkAAIB1N28w6YeT3FlKeU+SOwa3U0o5V0r5qSSptX4kySuT\nvH3w3w8O7kuSlyb5gVLK7yX52iQvmbM9sBAykwAAAKBv32lu09RaP5x+RtHe++9L8k0jt1+X5HVj\ntvujJM+epw2wDEJJAAAA0DdvZhKshZ5oEgAAACQRTIJWmmluRY4SAAAAa04wCVoQQgIAAIA+wSRo\nQQFuAAAA6BNMghbEkgAAAKBPMAlaaGJJgkoAAACsO8EkaEEQCQAAAPoEk6CFnmgSAAAAJBFMglbE\nkgAAAKBPMAlaKSP/BwAAgPUlmAQt9ESRAAAAIIlgErRimhsAAAD0CSZBC8UENwAAAEgimAStNJlJ\nRYoSAAAAa04wCVroCSIBAABAEsEkAAAAAA5AMAlakJgEAAAAfYJJ0EJTgFtMCQAAgHUnmAQt9ESR\nAAAAIIlgErRimhsAAAD0CSZBC0U0CQAAAJIIJkErTSxJTAkAAIB1J5gELRSltwEAACCJYBK0IiMJ\nAAAA+gSToAWxJAAAAOgTTIIWeoPUJIW4AQAAWHeCSdCCGBIAAAD0CSZBC2JJAAAA0CeYBC08/obL\n8qybr+q6GQAAANC5za4bAKvgzsdckzsfc03XzQAAAIDOyUwCAAAAoDXBJAAAAABaE0wCAAAAoDXB\nJAAAAABaE0wCAAAAoDXBJAAAAABaE0wCAAAAoDXBJAAAAABaE0wCAAAAoDXBJAAAAABaE0wCAAAA\noDXBJAAAAABaE0wCAAAAoDXBJAAAAABaE0wCAAAAoDXBJAAAAABaE0wCAAAAoDXBJAAAAABaE0wC\nAAAAoDXBJAAAAABaK7XWrttwYKWUDyX5o67b0YGrktzfdSNYW/ofXdMH6ZL+R9f0Qbqk/9E1fXB5\nHl5rvXq/jVYymLSuSin31VrPdd0O1pP+R9f0Qbqk/9E1fZAu6X90TR88ekxzAwAAAKA1wSQAAAAA\nWhNMWi2v7boBrDX9j67pg3RJ/6Nr+iBd0v/omj54xKiZBAAAAEBrMpMAAAAAaE0wCQAAAIDWBJMA\nAAAAaE0w6Qgqpfhe6EQppXTdBtZbKWWj6zawvkoplw5+Og7TiVLKQwc/HY9ZulLKY0spp7puB+ur\nlPLMUsqjum4H7RgsHRGllNtKKd+eJLXW7a7bw3oZ9L9/muSlpZSru24P66eUcq6U8oYkf9cggmUq\npfRKKZeUUn45yasTx2GWr5Ty5FLKW5K8MkmqFXJYolLKE0opv5XkVUmu7Lo9rJ9SylNKKf9Xkn+X\n5NKu20M7gklHQCnl3iT/Z5LvK6U8f3Cfq/MsXCllo5Ty99NfavNtSZ6S5BWllGu6bRnrYnAi/xNJ\nXpPkLUmuTfIDpZQz3baMdTEIHP1lkq0k15dSviqRncRylL5/lOSfJ3l9rfV/7rpNrKXvS/J/1Fq/\nrNb6gUR2HMtRStkqpbwm/XORVyd5U5LbB485Dh9xvqCj4Q+SfFGSFyf5niSptZ63E2cJekn+OMkL\na60/k+TeJE9PcrrLRrE+Bify/y7Jcwd98B8kqUke7LJdrJ1bktyf5MeT/PVSysW11m3HYRZtkIF0\nUZL/p9b6z5OklPIoJ1Esw+CCziOTfLzW+uOD++4spVyWZGNw236QRTqZ5DeSPKvW+stJfiHJraWU\nTVnCR58DVQdKKU8vpTx65K5fSfJ7g58fb6a7ZbATh8O0p/9tJ/nZWuu7Sykna61/kuT9Sa7qroUc\nd3v3gbXWf11r/Vgp5c4k96WfnfRDpZRbO2skx9Zo/xs5SfqDJA8k+cPBf/eUUm401YhFGDMOfEmS\np5VSvr+U8rYk/zDJz5RSntpNCznORvvf4GT9/iTPKqV8YSnlF5N8V/oZIv/LYBv7QQ7Vnn3gX9Va\n/2Wt9ZOD25tJztdaHxRUP/p8QUtUSrmslPIrSd6c5IWllLPNQ7XW87XWTyX50STfWEq5qtbqyjyH\nZkz/u2jQ7z6WJLXWT5dSLk7yiCR/0mVbOZ4m7QNHTug/muRraq13Jvmr9E/oTbnkUIzrfyMnSeeS\n/EWt9V1J3pXkFUl+cpB+b6zEoZi0D6y1/kWSf5LkK9LPUP/qJB9M8uXqGHJY9ul/P51+va7X1Vqf\nl+Snkjy9lPL0zhrMsTPpODyY7tsca38jyZeVUi6XmXT0GSAt19n054F+2+D3ZycXFPp8a5L/NNgm\npZTblttEjrG9/e9ZY7Z5WpJ31Vr/pJRyUSnl5mU2kGNv0j6wDn7eV2v9t4NtfzXJk5N8ooN2cjyN\n7X8Df5zk4lLKv0ry3Ul+J8m7a62fMZjlEE3sg7XWVye5vdb6m7XWTyf5xfSDnPaBHJZp+8BfTnJT\nkssHt+9L8mdJPr3E9nH8TRwHDqaW95K8d7DN53fVSNoTTFqwUsrXlVI+v5RyyaCg3WuT/FyST6Wf\n0nzdYLuS9Gslpb+SwktLKf8jyVPMVWZWB+h/m4OnXJbkfaWUb0jy9iRP6qLdHB9t++AYT03/yrwM\nTWZ2gP53eZKrk/xp+kHMFyf5bFMtmddB9oG11o+OPPWp6U87P7/UBnOstOh/1ydJrfX30p/W9q2l\nlKuS/I0kj0vy4Y6azjFxkHPhwcWbk4Onfqq5v4t2004xDfbwDTr9Q5P8y/Rr0vx/6Udfv6PWev9g\nm2cmeWGSt9da/8Xgvl6SR6afavpAkntrrf/v8v8FrLJZ+9/g/jck+etJXp/kHw0GF3Agc+wDL0k/\nO+6H0j+pf0mt9d3L/xewyg7Y/+6rtb5hcN9VI49flORErfUjHfwTWHFz7ANPJnlGkh9JP5huH8iB\nzboPHNz/d9I/F7k5yXfWWv/rkpvPMTDHPnBjsAjVv0jyB7XWH+ii/bQnM+mQDf4IapKLk3yg1vrc\n9K9wfiT9SGySpNb6tvTT+G4ppVxaSjkziMb+RZK/W2t9rkASBzVj/7tkcOKU9IvAv7DW+g0CScxi\njn3gqUHdhprkVbXWL3YSxUHN0P8+e9D/ztZa7y+lbJRSerXWjwskMYs59oGnB9PbHoh9IDOaYx94\n8eD+H0s/iPQ8gSRmMee5cJOJ+TcFklaDzKRDUkrZSL9w3UaSf5vkkiRfUWu9Z/B4L/2ixl9Va/2N\nwX0XpT+l7XOTPDzJU2ut7++g+ay4OfvfM5PcmORJtdYPdtB8joFD6oNPrv0VBeFADukYrP8xM/tA\numQfSNf0wfUkM+kQlFI+P/1inZenv7zwK5N8JslzmgLag6yjHxj81/jCJH87yTuTPF4giVkcQv/7\n3fT7n0ASMznEPmgAwYEd4jFY/2Mm9oF0yT6QrumD62tz/01oYTvJj47UXXhy+sur/90kP5nkqYNo\n7C8m+YJSyk211vemX1jsjlrrb3bTbI4J/Y+u6YN0Sf+ja/ogXdL/6Jo+uKZkJh2O30nyc4P0viR5\nW5Iba60/k2SjlPJtg2jsDUnOD/54Umt9oz8eDoH+R9f0Qbqk/9E1fZAu6X90TR9cU4JJh6DW+ola\n66dHiobdmeRDg9+/IcmtpZRfTvKzSd6RWOaQw6P/0TV9kC7pf3RNH6RL+h9d0wfXl2luh2gQja1J\nrknyS4O7/zLJy5M8Lskf1lo/kCRV5XMOmf5H1/RBuqT/0TV9kC7pf3RNH1w/MpMO13aSrST3J3nC\nIAL7/Um2a62/1fzxwILof3RNH6RL+h9d0wfpkv5H1/TBNVMEBQ9XKeXpSX578N9P11r/WcdNYo3o\nf3RNH6RL+h9d0wfpkv5H1/TB9SKYdMhKKTck+dokP1Zr/XTX7WG96H90TR+kS/ofXdMH6ZL+R9f0\nwfUimAQAAABAa2omAQAAANCaYBIAAAAArQkmAQAAANCaYBIAAAAArQkmAQAAANCaYBIAwAGVUs6X\nUn63lPKuUso7SykvKaVMHVeVUm4qpXzNstoIALAogkkAAAf3yVrrk2qtj01yZ5LnJ3nFPs+5KYlg\nEgCw8kqttes2AACslFLKx2utF43cfmSStye5KsnDk7whydnBw99aa/3tUsp/SnJrkj9M8vokr07y\nw0luT3IyyT+ptb5maf8IAIAZCSYBABzQ3mDS4L6PJfnsJH+ZZLvW+qlSys1JfrbWeq6UcnuS76q1\nftFg+xcleUit9VWllJNJ3pbkK2utf7jUfwwAwAFtdt0AAIBjZivJT5RSnpTkfJJHT9juriRPKKV8\nxeD2pUluTj9zCQDgyBJMAgCY02Ca2/kkf55+7aQ/S/LE9OtTfmrS05J8W631TUtpJADAIVGAGwBg\nDqWUq5P8b0l+ovbrB1ya5IO11u0kX5tkY7DpXya5eOSpb0ry4lLK1uB1Hl1KORsAgCNOZhIAwMGd\nLqX8bvpT2h5Mv+D2jw0e+1+T/EIp5euS/FqSvxrc/3tJzpdS3pnkZ5L84/RXeHtHKaUk+VCSL13W\nPwAAYFYKcAMAAADQmmluAAAAALQmmAQAAABAa4JJAAAAALQmmAQAAABAa4JJAAAAALQmmAQAAABA\na4JJAAAAALT2/wPK0YLrnykkLAAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize = (20,10))\n",
+ "spy.log_return.plot()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABI8AAAJCCAYAAABJU+dSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3WuQ5fl91/fPry/Tt+nLXLpnZm+a3ZVW8hqsC2uBZbCC\nFJOUTbAJFBUCRKEMTqWoFIFUgkOlUlCVKiAPIDxIKBtcKYVLxWDAJtwKWZZlwFjS6uKVtCvtSnud\na/fM9Onb6e7Tl38enO7RWt7Z6d3t0/9zeb2qtmb6cvp8d/fBTr33+/v9S1VVAQAAAIA3MlT3AAAA\nAAB0L/EIAAAAgHsSjwAAAAC4J/EIAAAAgHsSjwAAAAC4J/EIAAAAgHsSjwAAAAC4J/EIAAAAgHsS\njwAAAAC4p5G6BziK8+fPV5cvX657DAAAAIC+8cUvfvFWVVXz9/u+nohHly9fztNPP133GAAAAAB9\no5TyylG+z7E1AAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAA\nAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQj\nAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADgnsQjAAAAAO5JPAIAAADg\nnsQjAADu2tuv8lf+1XP5U5/8Qr52daXucQCALiAeAQBw11/5l8/lpz/7Yn79xTv5o3/717O80ap7\nJACgZuIRAABJkkazlb/3uVfyhz70UH7+v/2BrG/v5v/8zLfqHgsAqJl4BABAkuTnvvBatnb286d/\n6NG87+JMfvwDD+YffP7VbO3s1T0aAFAj8QgAgCTJv/jq9Xzwkbm87+JMkuQPfvDBNFt7+dXnl2qe\nDACok3gEAEAazVa+enUlH31i/u7nfuDxc5mdGM2//tqNGicDAOomHgEAkF9/8XaqKvnBd5+/+7nR\n4aF8/HsW8ulvLGZ/v6pxOgCgTuIRAAD599+6nalTw/nAw3O/6fMfefx8VjZ38sLiek2TAQB1E48A\nAMiXX1vOBx85k9Hh3/zHww9fPpsk+fzLd+oYCwDoAuIRAMCA29nbz/M31vO9D8z8lq89fHYiF2bG\n8vmXxCMAGFTiEQDAgHvh5npae/t58g3iUSklH370XJ62eQQAA0s8AgAYcM9eX02SN9w8SpL3PzSb\n6ytbubW+fZJjAQBdQjwCABhwX7+2konR4Tx6/vQbfv1wI+nr11ZPciwAoEuIRwAAA+4b19fyxMXp\nDA+VN/z6916aTdKOTADA4BGPAAAG3Eu3NvL4/NQ9vz47OZqHz07YPAKAASUeAQAMsI3t3dxY3crj\n8298ZO3Q916azdev2jwCgEEkHgEADLCXbm0kSR49f+/NoyR536XpvHKnmc3W3kmMBQB0EfEIAGCA\nHTUePXFhOlWVfHtp/STGAgC6iHgEADDADuPR5XNvHo/es9A+1vbC4lrHZwIAuot4BAAwwF5cWs+D\ncxOZODX8pt93+fxURoZKXrhp8wgABo14BAAwwF6508y7zk3e9/tGh4fy6PmpPC8eAcDA6Wg8KqXM\nlVJ+vpTyjVLKc6WUHyilnC2lfKqU8sLBr2c6OQMAAPd2ZXkzD5+5fzxK2vceObYGAIOn05tHfzPJ\nv66q6n1J3p/kuSQ/leTTVVW9J8mnDz4GAOCEbe3sZWltOw+dmTjS9z8+P5XX7jTT2t3v8GQAQDfp\nWDwqpcwm+aEkP5skVVW1qqpqJPmxJJ88+LZPJvnxTs0AAMC9XW1sJkkePGI8unx+KvtVcmW52cmx\nAIAu08nNo0eTLCX5v0spXy6l/J1SylSSC1VVXT/4nhtJLrzRi0spP1lKebqU8vTS0lIHxwQAGExX\nl9vx6KEjHlt718ET2V6+vdGxmQCA7tPJeDSS5ENJ/lZVVR9MspHvOqJWVVWVpHqjF1dV9TNVVT1V\nVdVT8/PzHRwTAGAwXbkbj464eXRwsfbLt2weAcAg6WQ8upLkSlVVnzv4+OfTjkk3SymXkuTg18UO\nzgAAwD1cWW5mZKjkwsz4kb7/7NSpTI+N5BWbRwAwUDoWj6qqupHktVLKew8+9fEkzyb5Z0k+cfC5\nTyT5xU7NAADAvV1Z3swDcxMZHipH+v5SSi6fn8pLt20eAcAgGenwz//vkvz9UsqpJC8m+ZNpB6t/\nWEr5iSSvJPkjHZ4BAIA3cLWxmQfnjnZk7dC7zk3mq1dXOjQRANCNOhqPqqr6SpKn3uBLH+/k+wIA\ncH83VrbyOx89+5Zec/ncVP7V125kZ28/o8OdvAEBAOgW/osPADCA9ver3FzdyoXZo913dOhd5yaz\nt1/dfVIbAND/xCMAgAF0a2M7u/tVLr3FeHT5/FSS5CWXZgPAwBCPAAAG0M2V7SQ58pPWDl0+145H\nr9wSjwBgUIhHAAAD6PpK+9jZW908On/6VKZODedlT1wDgIEhHgEADKCbq1tJkotvcfOolJJ3nZvK\nK46tAcDAEI8AAAbQ9ZWtjAyVnDs99pZfe/n8pM0jABgg4hEAwAC6sbqVhemxDA+Vt/zad52bymt3\nmtnbrzowGQDQbcQjAIABdGNlKxfe4n1Hhx46M5Hd/eru0TcAoL+JRwAAA2hxbTsXpt9uPJpMklxZ\n3jzOkQCALiUeAQAMoMXVrSzMvPX7jpL25lGSXFl27xEADALxCABgwGzt7GV1azfzb+Oy7CR5cO4w\nHtk8AoBBIB4BAAyYpbXtJHnbm0fjo8OZnx7LVfEIAAaCeAQAMGCW1tvxaH767cWjpH107UrDsTUA\nGATiEQDAgFlcPdg8epsXZiftS7MdWwOAwSAeAQAMmOPaPLrW2MzefnVcYwEAXUo8AgAYMEtr2ykl\nOTd16m3/jIfOTGRnr8ri2tYxTgYAdCPxCABgwCytbeXc1KmMDL/9Pwo+dGYyiSeuAcAgEI8AAAbM\n0tp25t/BfUdJe/MoSa4suzQbAPqdeAQAMGCW1rZz/vTbP7KWJA/OtePRVZtHAND3xCMAgAFza72V\n+dNv/7LsJBkfHc7502OOrQHAABCPAAAGzJ2NVs6+g8uyDz10ZkI8AoABIB4BAAyQZms3mzt7OfcO\nN4+Sw3jkziMA6HfiEQDAALm93kqSnDuWzaPJXG1sZn+/esc/CwDoXuIRAMAAub1xEI/e4YXZSfLg\n3Hh29qrcWt9+xz8LAOhe4hEAwAC5s9EOPcdx59Gl2fYT166tbL3jnwUAdC/xCABggNw6OLZ2/hju\nPHpg7iAeNVyaDQD9TDwCABggdw6OrR3H5tEDc+NJxCMA6HfiEQDAALm9vp3x0aFMnhp+xz9rdmI0\nk6eGc63h2BoA9DPxCABggNzeaOXc1FhKKe/4Z5VScml2PNdXbB4BQD8TjwAABsjt9daxPGnt0ANz\nE46tAUCfE48AAAbInY3Wsdx3dOiB2QlPWwOAPiceAQAMkNvr2zk39c6ftHbo0tx4lta2s727d2w/\nEwDoLuIRAMCAqKqqfefRMR9bS5KbK9vH9jMBgO4iHgEADIiN1l62d/dz7piPrSXJNZdmA0DfEo8A\nAAbEnfVWkhzvnUdz40ni0mwA6GPiEQDAgLi10T5adv70Md55dLB5dN2l2QDQt8QjAIAB0YnNo4lT\nwzkzOZqrNo8AoG+JRwAAA+L2webRcV6YnbQvzb4uHgFA3xKPAAAGxO2N9ubRuanjO7aWtI+uObYG\nAP1LPAIAGBC311uZGB3OxKnhY/25D86NO7YGAH1MPAIAGBB3NlrHfmQtSS7NTWRtazdrWzvH/rMB\ngPqJRwAAA+LW+nbOHeNl2YcuzY4n8cQ1AOhX4hEAwIC4s9E61ietHXpwbiJJcs3RNQDoS+IRAMCA\naDR3cqYTm0d345HNIwDoR+IRAMCAaDRbmZs4/nh0YXosQyW5vmLzCAD6kXgEADAAWrv72Wjt5czk\n6LH/7JHhoVyY8cQ1AOhX4hEAwABY2Ww/CW2uA/EoSR6Ym8h1x9YAoC+JRwAAA6DRbCVJZieP/9ha\n0n7immNrANCfxCMAgAHQONw8mujc5tG1la1UVdWRnw8A1Ec8AgAYAI1mOx6d6eDmUWt3P7c3Wh35\n+QBAfcQjAIABcHhsrVN3Hl2anUiS3Fhx7xEA9BvxCABgABxuHs12LB6NJxGPAKAfiUcAAAOgsdnK\n8FDJ9NhIR37+YTy6vioeAUC/EY8AAAZAo7mTuYnRlFI68vPPnR7L8FDJDU9cA4C+Ix4BAAyAxuZO\nx46sJcnwUMmF6bFcd2wNAPqOeAQAMAAazVbmJjoXj5Lk4uy4O48AoA+JRwAAA6DR3MmZyVMdfY9L\nsxPiEQD0IfEIAGAANJqdPbaWtDePrq9spaqqjr4PAHCyxCMAgAHQPrbW6c2j8Wzu7GV1c7ej7wMA\nnCzxCACgz7V297PR2svcCWweJcn1VU9cA4B+Ih4BAPS5lc2dJMmZDsejS4fxyL1HANBXxCMAgD63\nstlKksx2+MLsi7MTSeLSbADoM+IRAECfW262N4/mJjq7ebQwPZZSbB4BQL8RjwAA+lyjeXhsrbOb\nR6PDQ5k/PZYbK+48AoB+Ih4BAPS5RrN9bK3TF2Yn7XuPbB4BQH8RjwAA+tzh5tHsCcSji7Pj7jwC\ngD4jHgEA9LnGZivDQyXTYyMdf69LsxO5sSoeAUA/EY8AAPpco7mTuYnRlFI6/l4XZ8eztrWb9e3d\njr8XAHAyxCMAgD7X2Nw5kSNrSfvOoySOrgFAH+loPCqlvFxK+Wop5SullKcPPne2lPKpUsoLB7+e\n6eQMAACDrtFsZW7iZOLRxRnxCAD6zUlsHv3eqqo+UFXVUwcf/1SST1dV9Z4knz74GACADmk0d3Jm\n8tSJvNel2YkkyfWVzRN5PwCg8+o4tvZjST558PtPJvnxGmYAABgYjebJHVtbmBlLYvMIAPpJp+NR\nleTflFK+WEr5yYPPXaiq6vrB728kudDhGQAABtrK5k7mJk5m82h8dDjnpk7luieuAUDf6PTzWn93\nVVVXSykLST5VSvnG679YVVVVSqne6IUHseknk+SRRx7p8JgAAP2ptbuf9e3dzJ3Q5lGSXJgZt3kE\nAH2ko5tHVVVdPfh1Mck/TfLhJDdLKZeS5ODXxXu89meqqnqqqqqn5ufnOzkmAEDfWtncSZKcOcF4\ndGl2PNfFIwDoGx2LR6WUqVLK9OHvk/y+JF9L8s+SfOLg2z6R5Bc7NQMAwKBb2WwlSWZP6MLsJLk4\nO54bLswGgL7RyWNrF5L801LK4fv8g6qq/nUp5QtJ/mEp5SeSvJLkj3RwBgCAgbbcbG8ezU2c7ObR\ncnMnWzt7GR8dPrH3BQA6o2PxqKqqF5O8/w0+fzvJxzv1vgAAfEejeXhs7SQ3jyaStJ+4dvn81Im9\nLwDQGZ1+2hoAADVqNNvH1k7ywuxLs+NJ4t4jAOgT4hEAQB87vDB79gTj0cWDeHRj1b1HANAPxCMA\ngD623GxleKhkeqyTV13+ZhdnbB4BQD8RjwAA+lijuZO5idEcPMTkREyNjWRmfCQ3xCMA6AviEQBA\nH2ts7pzokbVDl2YnbB4BQJ8QjwAA+lij2crcxMnHo4uz4zaPAKBPiEcAAH2s0dzJ3OSpE3/fS7Pj\nubEqHgFAPxCPAAD6WDse1bN5dGt9O63d/RN/bwDgeIlHAAB9bGVzJ3MTJ795dHFmPFWV3LR9BAA9\nTzwCAOhTrd39rG/v1rJ5dGF2PEmyuCYeAUCvE48AAPrUyuZOkuRMHcfWZtrx6Obq9om/NwBwvMQj\nAIA+tbLZSpLM1nBh9oWDeOSJawDQ+8QjAIA+tdxsbx7NTZz85tGZydGcGh7KTcfWAKDniUcAAH2q\ncRiPaji2VkrJwsxYbto8AoCeJx4BAPSpRrN9bO1MDcfWkva9R+48AoDeJx4BAPSpwwuzZ2vYPEra\n9x7dXLV5BAC9TjwCAOhTy81WhodKpsdGanl/8QgA+oN4BADQpxrNncxNjKaUUsv7X5gZy0ZrL2tb\nO7W8PwBwPMQjAIA+1djcqe3IWpJcnB1PEvceAUCPE48AAPrUysHmUV0Wpg/jkaNrANDLxCMAgD61\n3GxlrqYnrSWv3zwSjwCgl4lHAAB9qtHcyVyNx9YuzIwlSW6IRwDQ08QjAIA+tbK5k7mJ+jaPJk+N\nZHp8JDdXxCMA6GXiEQBAH2rt7md9e7fWzaMkuTAz7sJsAOhx4hEAQB9a2dxJkpypOR5dnBl3bA0A\nepx4BADQh1Y2W0mS2RovzE6ShZmxLIpHANDTxCMAgD7UaLY3j+Ym6t88Wlzbzv5+VescAMDbJx4B\nAPSh5cN41AV3Hu3uV7m90ap1DgDg7ROPAAD6UKPZjjVnaj62dmFmPEly09E1AOhZ4hEAQB86vDB7\ntvbNo7Ek4hEA9DLxCACgDy03WxkeKpkeG6l1jouz7c0jT1wDgN4lHgEA9KFGcyezE6MppdQ6x/zp\nsZSS3FzdrnUOAODtE48AAPpQY3On9suyk2RkeCjnT4/l5orNIwDoVeIRAEAfWmnuZG6i/niUJBdn\nxnNzTTwCgF4lHgEA9KHlZitzNT9p7dCFmbHcsHkEAD1LPAIA6EONZnccW0uSCzPjWVxz5xEA9Crx\nCACgD61s7mRuols2j8ZzZ6OV7d29ukcBAN4G8QgAoM/s7O1nfXu3azaPLs6MJ0kWPXENAHqSeAQA\n0GcazZ0k6Zp4tDAzliS5uereIwDoReIRAECfWdlsJUnXXJh9cba9eXTT5hEA9CTxCACgz9zdPJro\njs2jC9PteHTD5hEA9CTxCACgzyx32bG1ucnRnBoZyqJ4BAA9STwCAOgzjWb72NqZLjm2VkrJhZkx\nm0cA0KPEIwCAPrOy2d48mu2SzaOk/cQ1F2YDQG8SjwAA+kyjuZPhoZLpsZG6R7lrYWbchdkA0KPE\nIwCAPrPcbGV2YjSllLpHuetw86iqqrpHAQDeIvEIAKDPNDZ3uuay7EMXZsbSbO1lbXu37lEAgLdI\nPAIA6DMrzZ3MTXRbPBpPktxcce8RAPQa8QgAoM8sN1uZ65InrR1amG7Ho8U19x4BQK8RjwAA+kyj\n2X3H1hZmxpIki2s2jwCg14hHAAB9ZmVzJ3MT3bZ5dBCPPHENAHqOeAQA0Ed29vazvr3bdZtHp8dG\nMjE67NgaAPQg8QgAoI80mjtJ0nXxqJSShZkx8QgAepB4BADQR1Y2W0nSdRdmJ+2ja4ur7jwCgF4j\nHgEA9JG7m0cT3bV5lCQLM+NZsnkEAD1HPAIA6CPdemwtOdg8Eo8AoOeIRwAAfWS5eXBsrcuetpYk\nC9PjWd/eTbO1W/coAMBbIB4BAPSRlc2DzaOp7tw8SpLFVdtHANBLxCMAgD7SaO5keKhkemyk7lF+\ni4WZdjy66dJsAOgp4hEAQB9ZbrYyOzGaUkrdo/wWC9PjSeLeIwDoMeIRAEAfaWzudOVl2cnrjq2J\nRwDQU8QjAIA+stLcydxEd8ajucnRnBoeyuKaY2sA0EvEIwCAPtLYbGVusvuetJYkpZTMT49lyYXZ\nANBTxCMAgD6yvNG9m0dJMj895tgaAPQY8QgAoI80mq3MdumdR0n73iPH1gCgt4hHAAB9orW7n43W\nXs506bG1JFmYsXkEAL1GPAIA6BONzVaS5ExXbx6Np9HcyfbuXt2jAABHJB4BAPSJRnMnSbr2wuwk\nuTAzliRZsn0EAD1DPAIA6BPLG4ebR90bjxamx5PE0TUA6CHiEQBAn1i+u3nUvcfW5qfbm0eLq+IR\nAPSKjsejUspwKeXLpZR/fvDxo6WUz5VSvlVK+blSSvf+rzEAgB7SaB5sHk117x+vFu4eW/PENQDo\nFSexefRnkzz3uo//WpK/UVXVu5MsJ/mJE5gBAKDvHW4edfOF2eemxjJUkps2jwCgZ3Q0HpVSHkry\no0n+zsHHJcnHkvz8wbd8MsmPd3IGAIBB0Wi2cmpkKBOjw3WPck/DQyXnT49l0eYRAPSMTm8e/R9J\n/qck+wcfn0vSqKpq9+DjK0kefKMXllJ+spTydCnl6aWlpQ6PCQDQ+5abrZyZHE37/9d1r4WZMRdm\nA0AP6Vg8KqX8/iSLVVV98e28vqqqn6mq6qmqqp6an58/5ukAAPrPcnOnq5+0dmhhetyF2QDQQ0Y6\n+LN/MMkfKKX8SJLxJDNJ/maSuVLKyMH20UNJrnZwBgCAgdFotrr6SWuHFqbH8syVlbrHAACOqGOb\nR1VV/c9VVT1UVdXlJP9Fkl+uquqPJflMkj988G2fSPKLnZoBAGCQ9M7m0Vhub2xnd2///t8MANTu\nJJ629t3+QpI/X0r5Vtp3IP1sDTMAAPSd9uZR98ej+ZnxVFVye6NV9ygAwBF08tjaXVVV/UqSXzn4\n/YtJPnwS7wsAMCiqqkqjuZMzPXJsLUkWV7dzYWa85mkAgPupY/MIAIBjtra9m939qieOrR0Go8W1\nrZonAQCOQjwCAOgDjY2dJOmZC7OTZHHNE9cAoBeIRwAAfWC52b4/qBfuPDp/+jvH1gCA7iceAQD0\ngcN41At3Hp0aGcrZqVOOrQFAjxCPAAD6wMrm4bG17t88StpH1xxbA4DeIB4BAPSB5Y3e2TxKkvnp\nsSyu2jwCgF4gHgEA9IHlZnvzaHaiN+LRwvS4zSMA6BHiEQBAH2g0W5kZH8nIcG/88W5hZixLa9vZ\n36/qHgUAuI/e+NMFAABvarm5kzNTvXHfUdK+82h3v7p70TcA0L3EIwCAPrDcbPXMZdlJ+9haEkfX\nAKAHiEcAAH2g0dzpmcuyk/axtUQ8AoBeIB4BAPSB5WYrZ3pq8+ggHnniGgB0PfEIAKAPNJo7meul\nzSPH1gCgZ4hHAAA9rrW7n/Xt3Z7aPJo4NZzpsZEsiUcA0PXEIwCAHtfYbD+xrJfuPEqS+Zkx8QgA\neoB4BADQ4xrNnSTpqaetJe17jxbX3HkEAN1OPAIA6HHLG4ebR70Wj8bdeQQAPUA8AgDocct3N496\n69jawvRYFle3U1VV3aMAAG9CPAIA6HGNZnvzqNfi0fz0WDZ39rK+vVv3KADAmxCPAAB63OHmUc8d\nW5sZSxJH1wCgy4lHAAA9rtFs5dTwUCZPDdc9yluyMD2eJFlcFY8AoJuJRwAAPa7R3Mnc5GhKKXWP\n8pYsTB9uHnniGgB0M/EIAKDHLTdbPXdkLfnO5tGSY2sA0NXEIwCAHne4edRrZiZGcmpkSDwCgC4n\nHgEA9Lhe3TwqpWRhesyF2QDQ5cQjAIAet9zcyZmp3ts8SnIQj9x5BADdTDwCAOhhVVWl0Wxlrgc3\nj5JkfnrM09YAoMuJRwAAPWx1aze7+1XOTfVmPFqYHndsDQC6nHgEANDD7my0kiRnezYejWVlcydb\nO3t1jwIA3IN4BADQw+5stLd2ejYezYwliSeuAUAXE48AAHrY7fX25tG5qbGaJ3l7FqbHk8TRNQDo\nYuIRAEAPOzy21qtPW5uftnkEAN1OPAIA6GG3N3p88+jusbWtmicBAO5FPAIA6GF3NlqZGB3OxKnh\nukd5W85NjWWoOLYGAN1MPAIA6GHLG62evSw7SYaHSs6fHsviqngEAN1KPAIA6GG3N1o5d7p341HS\nvvdo0bE1AOha4hEAQA+70+ObR0myMD3m2BoAdDHxCACgh/VHPBoXjwCgi4lHAAA97PbGds5O9ng8\nmhnL7fXt7O1XdY8CALwB8QgAoEc1W7vZ2tnP2R6/82hheiz7VXJ73fYRAHQj8QgAoEfdXm8lSc71\n+LG1+enxJHF0DQC6lHgEANCj7my049HZqbGaJ3lnFmba8y+JRwDQlcQjAIAedad5GI96e/NoYbod\njxbXtmqeBAB4I+IRAECPutM3x9YO4tGqzSMA6EbiEQBAj7p7bK3HL8weGxnO7MSoO48AoEsdKR6V\nUv5JKeVHSyliEwBAl7i90crocMn02Ejdo7xjC9Njjq0BQJc6agz6v5L8l0leKKX81VLKezs4EwAA\nR3BnYztnJk+llFL3KO/YwsyYzSMA6FJHikdVVf1SVVV/LMmHkryc5JdKKb9WSvmTpZTRTg4IAMAb\nu7PR6vnLsg8tTI+78wgAutSRj6GVUs4l+a+T/KkkX07yN9OOSZ/qyGQAALyp2xutnOvx+44OLUyP\nZWltO1VV1T0KAPBdjnRAvpTyT5O8N8nfTfKfVVV1/eBLP1dKebpTwwEAcG/LG608dGau7jGOxfz0\nWFp7+1nZ3MncZH8EMQDoF0e9XfFvV1X1L1//iVLKWFVV21VVPdWBuQAAuI/bG62c65djazPjSZKl\ntW3xCAC6zFGPrf1vb/C5/3CcgwAAcHTbu3tZ29rtozuPxpLEpdkA0IXedPOolHIxyYNJJkopH0xy\n+CiPmSSTHZ4NAIB7uL3eSpKcPz1W8yTH4zvxaKvmSQCA73a/Y2v/SdqXZD+U5K+/7vNrSf5ih2YC\nAOA+bq23N3TO98mF2fOH8cgT1wCg67xpPKqq6pNJPllK+UNVVf3jE5oJAID7uBuPpvtj8+j02Egm\nRocdWwOALnS/Y2t/vKqqv5fkcinlz3/316uq+utv8DIAADrs1lr72Np8nxxbK6VkYWZMPAKALnS/\nY2tTB7+e7vQgAAAc3dLB5tF8n2weJe17jxZX3XkEAN3mfsfWfvrg1798MuMAAHAUS2vbOT02kvHR\n4bpHOTYL0+N57vpq3WMAAN9l6CjfVEr530spM6WU0VLKp0spS6WUP97p4QAAeGO31rf75rLsQ/PT\njq0BQDc6UjxK8vuqqlpN8vuTvJzk3Un+x04NBQDAm2vHo/45spYkCzNjWd/eTbO1W/coAMDrHDUe\nHR5v+9Ek/6iqqpUOzQMAwBHcWm/1XzyaHk/SPpIHAHSPo8ajf15K+UaS35Hk06WU+SRuMwQAqMmt\n9e2cn+6vY2sLB5d/O7oGAN3lSPGoqqqfSvKRJE9VVbWTZCPJj3VyMAAA3tjO3n4azZ3Mnx6ve5Rj\ntTDTjkc3PXENALrKmz5t7bu8L8nlUsrrX/P/HPM8AADcx+31VpL03ebRxZl2DLuxIh4BQDc5Ujwq\npfzdJI+Dj6CgAAAgAElEQVQn+UqSvYNPVxGPAABO3K319rGufrvzaHZiNKdGhmweAUCXOerm0VNJ\nnqyqqurkMAAA3N9Sn8ajUkouzoznxqo7jwCgmxz1wuyvJbnYyUEAADiaw6eRzfdZPEraR9dsHgFA\ndznq5tH5JM+WUj6f5O7/Cqqq6g90ZCoAAO7p7rG1PrvzKEkuzI7nmSuNuscAAF7nqPHoL3VyCAAA\nju7WWiuTp4YzeeqtPPukN1ycGcu/WdlKVVUppdQ9DgCQIx5bq6rqs0leTjJ68PsvJPnSm72mlDJe\nSvl8KeU3SilfL6X85YPPP1pK+Vwp5VullJ8rpfTf/zIDAOigW+vbmZ/uvyNrSXJhZjzbu/tZ2dyp\nexQA4MCR4lEp5U8n+fkkP33wqQeT/MJ9Xrad5GNVVb0/yQeS/KellN+V5K8l+RtVVb07yXKSn3g7\ngwMADKpb69t9d1n2oYuz40mSG+49AoCucdQLs/9Mkh9MspokVVW9kGThzV5Qta0ffDh68FeV5GNp\nh6gk+WSSH3+LMwMADLR2POrP5e2LMwfxaEU8AoBucdR4tF1VVevwg1LKSNoh6E2VUoZLKV9Jspjk\nU0m+naRRVdXuwbdcSXuLCQCAI7q13urbzaMLB/HIE9cAoHscNR59tpTyF5NMlFJ+OMk/SvL/3e9F\nVVXtVVX1gSQPJflwkvcddbBSyk+WUp4upTy9tLR01JcBAPS13b39LDf7Px7dWNm+z3cCACflqPHo\np5IsJflqkv8myb9M8r8c9U2qqmok+UySH0gyd7C5lLSj0tV7vOZnqqp6qqqqp+bn54/6VgAAfe3W\neitV9Z3I0m9OjQzl3NQpdx4BQBc50vNdq6raL6X8QpJfqKrqSGtApZT5JDtVVTVKKRNJfjjty7I/\nk+QPJ/l/k3wiyS++rckBAAbQYVS5MNOfm0dJO4w5tgYA3eNNN49K218qpdxK8s0k3yylLJVS/tcj\n/OxLST5TSnkmyReSfKqqqn+e5C8k+fOllG8lOZfkZ9/Z3wIAwOC4eTce9efmUdJ+4poLswGge9xv\n8+jPpf2Ute+vquqlJCmlPJbkb5VS/lxVVX/jXi+squqZJB98g8+/mPb9RwAAvEWLB/Fooc83j37j\ntUbdYwAAB+5359GfSPJHD8NRcjf+/PEk/1UnBwMA4Le6ubqd4aGSc1P9G48uzozn9kYr27t7dY8C\nAOT+8Wi0qqpb3/3Jg3uPRjszEgAA93JzdSvzp8cyPFTqHqVjLs62w9jiqieuAUA3uF88ar3NrwEA\n0AE317b7+rLs5Dv3Obk0GwC6w/3uPHp/KWX1DT5fkvTvLY0AAF1qcXUrD5+drHuMjro42/5j5g3x\nCAC6wpvGo6qqhk9qEAAA7u/G6laeunym7jE66uLB5pEnrgFAd7jfsTUAALrE1s5eGs2du3GlX81O\njGZsZMixNQDoEuIRAECPWFprXyC90OfxqJSSi7PjueHCbADoCuIRAECPONzEudDn8Shp/z3edGwN\nALqCeAQA0CNuHmzi9PvT1pJ2PHJhNgB0B/EIAKBH3N08mu7/zaOLM2O5sbqVqqrqHgUABp54BADQ\nI26ubeXU8FDmJkfrHqXjLsyMp7W7n0Zzp+5RAGDgiUcAAD1icXU7CzNjKaXUPUrHXZxtb1c5ugYA\n9ROPAAB6xI2VrYG4LDtJLs6IRwDQLcQjAIAecXNtayAuy05et3nkiWsAUDvxCACgRyyubg/M5tGF\nmfEMleR6Y7PuUQBg4IlHAAA9YGN7N+vbu1kYgCetJcno8FAuzIznasPmEQDUTTwCAOgB11faGzgP\nzA1GPEqSB+Ymcs3mEQDUTjwCAOgBhxs4D8xN1DzJybk0O343mgEA9RGPAAB6wOEGziDFowfnJnJt\nZSv7+1XdowDAQBOPAAB6wLXGZoZKcmF6MJ62lrRDWWt3P7c3WnWPAgADTTwCAOgBVxubuTgznpHh\nwfnj2+GWlXuPAKBeg/OnDwCAHna9sTVQR9aS71wOLh4BQL3EIwCAHnBtZTOXBi0ezR5sHq1s1TwJ\nAAw28QgAoMvt71cHm0fjdY9youYmRzMxOmzzCABqJh4BAHS5Wxvbae3t58EB2zwqpeSBuXHxCABq\nJh4BAHS5a432sa3DY1yD5IG5CfEIAGomHgEAdLnrB/Fk0C7MTpIH5yZyteHOIwCok3gEANDlrt6N\nR4N151HSDma31rezvbtX9ygAMLDEIwCALnetsZXJU8OZnRite5QTd2m2HcxueOIaANRGPAIA6HLX\nGpt5YG4ipZS6Rzlxh5eEX3XvEQDURjwCAOhy11Y2B/K+o+Q79zxdXRaPAKAu4hEAQJe71tjKgwN4\n31GSXJobTynJFfEIAGojHgEAdLGtnb3cWt/OpdnB3DwaGxnOxZnxvLbcrHsUABhY4hEAQBe7dnDX\nz4MDemwtSR4+M5krd2weAUBdxCMAgC726p32xs0j5yZrnqQ+D5+dvPvPAQA4eeIRAEAXe+0wHp0d\n5Hg0kZtrW9ne3at7FAAYSOIRAEAXe/VOM2MjQ5k/PVb3KLV5+MxkqsoT1wCgLuIRAEAXe/VOMw+f\nnczQUKl7lNo8fLB19Zp4BAC1EI8AALrYq3c2B/rIWvKdI3uvufcIAGohHgEAdKmqqnLlTnPg49HC\n9FhOjQyJRwBQE/EIAKBLNZo7WdvevXtsa1ANDZU8NDeR15bFIwCog3gEANClXvWktbseOjuZ1+64\n8wgA6iAeAQB0KfHoOx45a/MIAOoiHgEAdKnDePTw2YmaJ6nfw2cm02juZHVrp+5RAGDgiEcAAF3q\ntTvNnD89lslTI3WPUruHPXENAGojHgEAdKlX7zTziK2jJO3NoyTuPQKAGohHAABdqh2P3HeUfOfe\nJ5tHAHDyxCMAgC60s7efa41N8ejA7ORozkyO5qXbG3WPAgADRzwCAOhCV5c3s199564fkkfPT+Wl\nJfEIAE6aeAQA0IVevLWeJHlsfqrmSbrH5fNTednmEQCcOPEIAKALvXiwYfPY+dM1T9I9Hjs/lesr\nW9ls7dU9CgAMFPEIAKALvXhrI3OTozkzdaruUbrG5fPtLSzbRwBwssQjAIAu9OLSeh4778ja6z16\n8M/jpVviEQCcJPEIAKALvbi0kcfmHVl7vcvnxCMAqIN4BADQZda3d7O4tn1304a2qbGRXJgZE48A\n4ISJRwAAXebwcfSPe9Lab3H53FReFo8A4ESJRwAAXebFW+tJkkc9ae23eGx+yuYRAJww8QgAoMt8\ne2kjpSTvOjdZ9yhd5/K5qdzeaGVlc6fuUQBgYIhHAABd5qVbG3nozETGR4frHqXrHN4D5egaAJwc\n8QgAoMu8uLTuyNo93I1Ht8UjADgp4hEAQBepqiov3drIY5609oYeOTeZoZJ8e3G97lEAYGCIRwAA\nXeTm6naarb085klrb2hsZDiXz03l+ZviEQCcFPEIAKCLvLC4liR597xja/fyngun8/zBPycAoPPE\nIwCALvLNG+0o8sTF6Zon6V5PXJjOK7eb2d7dq3sUABgI4hEAQBd54eZ6zk6dyvnTY3WP0rXevXA6\ne/vtu6EAgM4TjwAAusg3b67liQuOrL2ZJy60t7LcewQAJ0M8AgDoElVV5VuL63fjCG/ssfmpDA+V\nvHDTvUcAcBLEIwCALnFtZSvr27vi0X2MjQznXecm87x4BAAnQjwCAOgSzx9eli0e3dcTC9N5wbE1\nADgR4hEAQJc43KRx59H9vefC6bx8e8MT1wDgBHQsHpVSHi6lfKaU8mwp5eullD978PmzpZRPlVJe\nOPj1TKdmAADoJd+8uZaF6bHMTZ6qe5Su954L09mvkheXPHENADqtk5tHu0n+h6qqnkzyu5L8mVLK\nk0l+Ksmnq6p6T5JPH3wMADDwXri5nvdedGTtKA63s9x7BACd17F4VFXV9aqqvnTw+7UkzyV5MMmP\nJfnkwbd9MsmPd2oGAIBesb9f5YXFtbxnQTw6ikfPT2VkqOSbN8QjAOi0E7nzqJRyOckHk3wuyYWq\nqq4ffOlGkgv3eM1PllKeLqU8vbS0dBJjAgDU5rXlZrZ29t13dERjI8N598LpPHt9te5RAKDvdTwe\nlVJOJ/nHSf77qqp+03/dq6qqklRv9Lqqqn6mqqqnqqp6an5+vtNjAgDU6rmDCPI9l2ZqnqR3PPnA\nTL5+TTwCgE7raDwqpYymHY7+flVV/+Tg0zdLKZcOvn4pyWInZwAA6AXPXlvNUIk7j96C731gNktr\n21lc26p7FADoa5182lpJ8rNJnquq6q+/7kv/LMknDn7/iSS/2KkZAAB6xbPXV/P4/OmMjw7XPUrP\nePJgS+tZ20cA0FGd3Dz6wSR/IsnHSilfOfjrR5L81SQ/XEp5Icl/fPAxAMBAe/baap58wJG1t+Lw\nn5ejawDQWSOd+sFVVf27JOUeX/54p94XAKDXLG+0cm1l6+4mDUczOzGah89OuDQbADrsRJ62BgDA\nvR1elm3z6K178tKMY2sA0GHiEQBAzQ43Z2wevXXf+8BsXrq1kfXt3bpHAYC+JR4BANTs2WuruTgz\nnnOnx+oepeccBrdvOLoGAB0jHgEA1OzZ6y7Lfru+90GXZgNAp4lHAAA12trZy7cW1x1Ze5suzozn\n/OlT+Y0rjbpHAYC+JR4BANTohZvr2d2v8j3i0dtSSsn7H5rLb7wmHgFAp4hHAAA1euZqO3p830Oz\nNU/Suz7w8Fy+vbSRlc2dukcBgL4kHgEA1OiZ11ZyZnI0D52ZqHuUnvWBR+aSJM84ugYAHSEeAQDU\n6JmrK/ntD82llFL3KD3r+x5qx6OvvCoeAUAniEcAADXZbO3l+Ztreb8ja+/I7MRoHp+fylfcewQA\nHSEeAQDU5NnrK9nbr/LbHxSP3qkPPHwmX3mtkaqq6h4FAPqOeAQAUJNnrqwkSd7/8FzNk/S+Dzwy\nl9sbrVxZ3qx7FADoO+IRAEBNnrmykoXpsVyYGa97lJ73gYN7j77s6BoAHDvxCACgJr9xpXH3smfe\nmfddms7YyFC+/Opy3aMAQN8RjwAAarC2tZMXlzbyfS7LPhajw0P5wMNzefpl8QgAjpt4BABQg68e\n3HckHh2fDz96Nl+/tpL17d26RwGAviIeAQDU4PBung8+fKbmSfrHU5fPZr+Ko2sAcMzEIwCAGnzp\nleU8Pj+V2cnRukfpGx96ZC5DJfnCS3fqHgUA+op4BABwwqqqypdfa+RDj9g6Ok7T46N58oGZfMG9\nRwBwrMQjAIAT9vLtZu5stPKhd4lHx+37L5/Nl19bTmt3v+5RAKBviEcAACfsS6+0N2NsHh2/7798\nNls7+/natZW6RwGAviEeAQCcsC+9upzpsZG8Z+F03aP0ne+/fDaJe48A4DiJRwAAJ+xLrzbygUfm\nMjRU6h6l78xPj+Wx81P5nHgEAMdGPAIAOEHr27v55o3VfNCRtY75yLvP5XMv3s7OnnuPAOA4iEcA\nACfomdca2a/aj5WnMz7y+PlstPbyzBX3HgHAcRCPAABO0OdfvpNS4klrHfQDj51Lkvzat27VPAkA\n9AfxCADgBH3h5Tv5noszmRkfrXuUvnVm6lSevDSTX/v27bpHAYC+IB4BAJyQnb39fOmVRj786Nm6\nR+l7P/juc/niq8vZ2tmrexQA6HniEQDACfna1ZVs7uyJRyfgI4+fT2t3P198ZbnuUQCg54lHAAAn\n5Asvtx8f//2XxaNO+/5Hz2ZkqOTfu/cIAN4x8QgA4IR8/qU7eez8VOanx+oepe+dHhvJ+x+ec+8R\nABwD8QgA4ATs71f5wsvLto5O0EceP5dnrjSyurVT9ygA0NPEIwCAE/D84lpWNnfcd3SCPvL4+exX\nyedfvFP3KADQ08QjAIAT8OsHx6fEo5PzwUfmMjYylH/n3iMAeEfEIwCAE/Br376dR85O5uGzk3WP\nMjDGR4fz4UfP5t++sFT3KADQ08QjAIAO29uv8usv3s5HHj9X9ygD56NPzOfbSxu5stysexQA6Fni\nEQBAh3392kpWt3bzA+LRifuP3jufJPnV5x1dA4C3SzwCAOiww8fFf+Tx8zVPMngenz+dB2bH89nn\nF+seBQB6lngEANBh//5bt/LEhdOZnx6re5SBU0rJR987n1/71u3s7O3XPQ4A9CTxCACgg1q7+/nC\ny3dsHdXoo0/MZ217N19+tVH3KADQk8QjAIAO+vKry9na2XdZdo0+8u7zGR4qjq4BwNskHgEAdNC/\nfeFWhodKfpd4VJuZ8dF86JE5l2YDwNskHgEAdNBnn1/K73jkTGbGR+seZaB99In5fPXqSm6tb9c9\nCgD0HPEIAKBDbq1v56tXV/LRg8fFU58feqL97+DfvrBU8yQA0HvEIwCADjkMFR99Qjyq2297YDZn\np045ugYAb4N4BADQIZ/95lLOnz6VJy/N1D3KwBsaKvmh95zPrz6/lP39qu5xAKCniEcAAB2wv1/l\nV1+4lR96z3yGhkrd45D20bXbG608e3217lEAoKeIRwAAHfC1ayu5s9Fy31EX+T3vaf+7+Ozz7j0C\ngLdCPAIA6IBPP7eYUpLf/e7zdY/Cgfnpsfy2B2fyK99crHsUAOgp4hEAQAf80nM38zseOZNzp8fq\nHoXX+dh7F/LFV5bTaLbqHgUAeoZ4BABwzK42NvP1a6v54Scv1D0K3+X3vm8h+5WjawDwVohHAADH\n7JeevZkk4lEXev9Dczk3dSq//A1H1wDgqMQjAIBj9kvP3cxj81N5bP503aPwXYaGSj763vl89vml\n7O1XdY8DAD1BPAIAOEarWzv59Rdv2zrqYh9/34U0mjv58qvLdY8CAD1BPAIAOEa/8s2l7OxV+eHv\nEY+61e954nxGhko+7egaAByJeAQAcIz+1VevZ356LB985Ezdo3APM+OjeerymXxGPAKAIxGPAACO\nycb2bn75G4v5kd92McNDpe5xeBMff9+FfOPGWq42NuseBQC6nngEAHBMPv2NxWzv7udHv++Bukfh\nPn7v+xaSxPYRAByBeAQAcEz+xTPXsjA9lqfe5chat3t8fiqPnJ3ML4tHAHBf4hEAwDFY397NZ765\nlB/57Zcy5Mha1yul5GPvW8ivfftWtnb26h4HALqaeAQAcAx+6dmbae3u5/d/36W6R+GIPva+hWzt\n7Oc/fPt23aMAQFcTjwAAjsE/+fLVPDg3kQ95ylrP+J2Pnc3kqeF8+hs36x4FALqaeAQA8A7dXN3K\nv3thKf/5hx50ZK2HjI0M53e/+3x++bnFVFVV9zgA0LXEIwCAd+gXvnw1+1XyBz/4YN2j8Bb98JMX\ncm1lK1+/tlr3KADQtcQjAIB3oKqq/OMvXcmHHpnLY/On6x6Ht+jj33MhQyX5N1+/UfcoANC1xCMA\ngHfg69dW///27jxMrqpe9/i7aux5Hsk8Jx1CAgkzGMQEgiCIwhVFREW5OBwPl3MVjlcuDwevB68D\neBQUFEQeLiKCMhuGMIlCSEJCCGSe00l3utOdHqq7a1z3j6rudIZKV9Ldtbu6v5/nqad27dpV9XYl\nq/auX621tjbUt+szp4x2OgqOQ0muT/PGl+ilj5j3CACAZCgeAQAA9MPjy3fK53ZxlrUMdkFNpdbV\ntWlnU4fTUQAAGJIoHgEAABynjlBEf32vVp+cVaWiHJ/TcXCcFtZUShK9jwAASILiEQAAwHF69v3d\nagtGdPUZ45yOgn4YV5qraZX5evkj5j0CAOBIBq14ZIx50Biz1xizpte6EmPMy8aYjYnr4sF6fQAA\ngMH26NIdmlKRp3njOKTJdAtrKrVsW7OaAyGnowAAMOQMZs+jhyQtOmTdLZKWWGunSFqSuA0AAJBx\n1tS26P1dLbr69LEyxjgdB/10wcxKRWNWr67b63QUAACGnEErHllr35TUdMjqyyT9IbH8B0mfHqzX\nBwAAGEwPv71NWV6XLucsa8PCrFGFqirI0ksMXQMA4DDpnvOo0lq7J7FcJ6kyza8PAADQb43tQT21\narc+e8poFWZ7nY6DAWCM0QUzK/XGhgZ1hCJOxwEAYEhxbMJsa62VZJPdb4y53hiz3BizvKGhIY3J\nAAAAju6Rd7YrFInpq+dMcDoKBtDFs6rVFY4xdA0AgEOku3hUb4yplqTEddI9s7X2fmvtPGvtvPLy\n8rQFBAAAOJqucFSPvLNd50+v0KTyPKfjYADNG1+i8ny/nl+9p++NAQAYQdJdPHpG0rWJ5WslPZ3m\n1wcAAOiXZ1btVmN7SNfR62jYcbuMLjqxSq+t38vQNQAAehm04pEx5o+S3pY0zRizyxhznaQ7JS00\nxmyUtCBxGwAAICNEY1a/eWOzaqoLdNakUqfjYBAwdA0AgMN5BuuJrbWfT3LXJwbrNQEAAAbTc6t3\na0tjQL+++hQZY5yOg0HQe+jaJSed4HQcAACGBMcmzAYAAMgksZjVr17dpKmVebpwZpXTcTBIGLoG\nAMDhKB4BAACkYPGHddq4t13fPn+KXC56HQ1nDF0DAOBgFI8AAAD6YK3VL1/dpInlubp4VrXTcTDI\nOOsaAAAHo3gEAADQh1fW7tXaPa361nmT5abX0bDndhldPKtaS9btVUtn2Ok4AAA4juIRAADAUURj\nVj97ab3GlebosjlMoDxSfOaUUQpFYvQ+AgBAFI8AAACO6qmVtVpX16b/ecE0edwcOo0Us0YVakpF\nnp58b5fTUQAAcBxHQAAAAEl0haP6+csbdNLoQuY6GmGMMfrMKaO1YnuztjYGnI4DAICjKB4BAAAk\n8fDb21S7v1O3LJrOGdZGoMtPHiWXkf5K7yMAwAhH8QgAAOAIWjrCuue1zZo/tVxnTS5zOg4cUFWY\npbMnl+nJ92oVi1mn4wAA4BiKRwAAAEdw7+ub1NoV1s2LpjsdBQ66Yu5o1e7v1NKtTU5HAQDAMRSP\nAAAADrGloV0P/mOrPnvKaNWcUOB0HDjogpoq5fk9TJwNABjRKB4BAAAc4o7nPpLf49b3Fk1zOgoc\nlu1z6+JZ1Xrhgz1q7Qo7HQcAAEdQPAIAAOjl1XX1em19g/71E1NUkZ/ldBwMAV84faw6QlE9tbLW\n6SgAADiC4hEAAEBCMBLVHc+t1cTyXF171nin42CImD2mSLNGFeqRd7bLWibOBgCMPBSPAAAAEn7/\nj23a2hjQ/76kRj4Ph0k44ItnjNWG+na9y8TZAIARiKMiAAAASfWtXfrlko1aMKNS502rcDoOhphL\nZ49SfpZHjyzd4XQUAADSjuIRAACApB//bZ3CUatbL5nhdBQMQdk+t66cO0Z/+2CP6lq6nI4DAEBa\nUTwCAAAj3ortzfrLylp9/WMTNK401+k4GKK+cvZ4xazVQ//c5nQUAADSiuIRAAAY0aIxq9ueWaPK\nAr++ed5kp+NgCBtTkqNFJ1bp0aXbFQhGnI4DAEDaUDwCAAAj2qNLt2tNbat+cHGNcv0ep+NgiPva\nuRPV2hXR48t3Oh0FAIC0oXgEAABGrMb2oH7y4nqdPblUl5xU7XQcZIBTxhZr7rhiPfDWVoWjMafj\nAACQFhSPAADAiPWfL6xTZziq2y89UcYYp+MgQ9wwf5J2NXfq6VW7nY4CAEBaUDwCAAAj0rJtTXry\nvV362rkTNbkiz+k4yCALZlSoprpA97y2SRF6HwEARgCKRwAAYMSJRGO69ak1GlWUrX85n0mycWyM\nMfrOJ6Zoa2NAz66m9xEAYPijeAQAAEach/65Tevq2nTrJTXK8TFJNo7dBTWVml6Vr1++Su8jAMDw\nR/EIAACMKPWtXbr7lY2aP7VcF86sdDoOMpTLZXTjgqna0hDQn1fscjoOAACDiuIRAAAYUX74/FqF\nojHdfulMJslGv1w4s1JzxxXr5y9vUEco4nQcAAAGDcUjAAAwYvxzU6OefX+3bpg/SePLcp2Ogwxn\njNH3PzldDW1B/e7vW52OAwDAoKF4BAAARoSucFQ/eHqNxpRk65vnTXI6DoaJueNKtGhmle57Y7Ma\n2oJOxwEAYFBQPAIAACPCva9t0paGgO647ERled1Ox8Ew8r1F09QViem/lmx0OgoAAIOC4hEAABj2\nNtS36ddvbNan55yg86ZVOB0Hw8zE8jx94bSxevTdHVpX1+p0HAAABhzFIwAAMKxFY1Y3P7laeX6P\nbr2kxuk4GKZuWjhVhdle/eCvaxSLWafjAAAwoCgeAQCAYe2Rd7Zr5Y79uvWSGpXm+Z2Og2GqONen\nWy6aruXbm/XEil1OxwEAYEBRPAIAAMPWtsaAfrx4nc6dUqbLTx7ldBwMc1ecMlqnji/Wf/5trZoC\nIafjAAAwYCgeAQCAYSkSjenGP62Sx2X0f684ScYYpyNhmHO5jH746Vlq64rozr+tdToOAAADhuIR\nAAAYln712iat2rlf/+fyWaouzHY6DkaIaVX5uu6cCXp8+S79c1Oj03EAABgQFI8AAMCws3JHs375\n6iZdfvIofWr2CU7HwQhz44KpmlCWq+8+sVptXWGn4wAA0G8UjwAAwLDS0hnWjX9apaqCLN1+2Uyn\n42AEyva59dMrZ2tPS6d+9MI6p+MAANBvFI8AAMCwEYtZ3fjYStU2d+oXV81RQZbX6UgYoeaOK9bX\nz52oP767Q29saHA6DgAA/ULxCAAADBt3L9mo19Y36LZP1Wje+BKn42CE+x8Lp2pyRZ5ufmK1WjoY\nvgYAyFwUjwAAwLDw5Ipd+q8lG3XF3NH64hnjnI4DKMvr1s//22w1tgd185OrZa11OhIAAMeF4hEA\nAMh4b25o0M1PrtbZk0v1o8tnyRjjdCRAknTS6CLdvGi6Fn9Yp0eW7nA6DgAAx4XiEQAAyGhLt+zT\nDY+s0JTKfP3mi3Pl83B4g6HlunMm6Lxp5brjuY+0dk+r03EAADhmHF0BAICM9fbmffry75epujBL\nf/jqqcpngmwMQS6X0U+vnK2ibK++/eh7CgQjTkcCAOCYUDwCAAAZafGaOn359+9qdHG2Hrv+TFXk\nZ38HoUkAABOcSURBVDkdCUiqLM+vu6+ao62NAX33ifeZ/wgAkFEoHgEAgIxirdUDb23VN/7fCs2o\nLtBj15+h8ny/07GAPp01qUz/ftEMvfBBne59fbPTcQAASJnH6QAAAACpag9G9P2/fKBn3t+tC2dW\n6u7Pnaxsn9vpWEDKvnbuBK3Z3aKfvrReNdUF+vj0CqcjAQDQJ3oeAQCAjLC+rk2X/uotPbd6t757\n4TT9+uq5FI6QcYwxuvMzJ6mmukDfeWylNta3OR0JAIA+UTwCAABDWjRm9bu/b9Glv3pLrZ0RPfK1\n0/Wtj0+Wy2WcjgYcl2yfW/ddM1dZXre+9OC72tPS6XQkAACOiuIRAAAYsrY2BvS5+97WD59fq7Mn\nl+mFfz1HZ00qczoW0G+ji3P00FdOVVtXRNc++K5aOsJORwIAICmKRwAAYMjpCkd19ysbtOjuN7Wh\nvk0/u3K2Hrh2HmdUw7Ay84RC3f+ludrW2KGvPbxMnaGo05EAADgiikcAAGDIsNZq8Zo6Lfj5G7r7\nlY1aWFOpl2+ar8/OHS1jGKaG4eesSWW663NztHx7s77y0LsKBCNORwIA4DCcbQ0AAAwJK7Y36+5X\nNujvGxs1rTJff/z6GTpzUqnTsYBBd/FJ1YrE5uimx9/XNQ8s1UNfPU0FWV6nYwEA0IPiEQAAcIy1\nVm9tatQ9r23SO1uaVJTj1W2fqtE1Z4yTx00HaYwcl80ZJZ/bpe88tlJX/3apHvrKqSrN8zsdCwAA\nSRSPAACAA2Ixq5c+qtM9r23WB7UtqirI0g8unqHPnzZWuX4OTzAyXTSrWvd5Xbrhkfd02T3/0G+/\nNE8zqgucjgUAgIy11ukMfZo3b55dvny50zEAAEA/haMxPb1qt37zxmZt2tuucaU5+sb8Sbr8lFHy\ne9xOxwOGhPd37tfXH16u9mBEd31uji6cWeV0JADAMGWMWWGtndfndhSPAADAYOsKR/WnZTt1/5tb\nVLu/U9Or8vXNj0/WJ0+sYngacAT1rV26/uHlen9Xi26YP0k3LZwqn4e2AgAYWKkWj+gXDgAABk17\nMKKH396mB9/aqsb2kOaOK9Ydn56pj0+r4OxpwFFUFmTpT//9TN3+7If6zRub9Y9NjfrFVXM0sTzP\n6WgAgBGInkcAAGDAdYWjeuSd7br39c1qCoT0sanl+tZ5k3TahBKKRsAxWrymTrf8ZbWC4Zi+t2ia\nvnTmeLldtCMAQP/R8wgAAKRdJBrTEyt26RdLNmpPS5fOmVymf7tgqk4eW+x0NCBjLTqxSiePLdL3\nnlit25/9SH9dWasfXT5LJ44qdDoaAGCEoOcRAADot1jM6vkP9uiulzdoS2NAs8cU6eYLp+msyWVO\nRwOGDWutnlu9R7c/+5GaO0L66tnjdeOCqZyhEABw3Oh5BAAABp21Vq+vb9BPXlyvj/a0amplnu6/\nZq4W1lQyPA0YYMYYfWr2CfrYlHL9+MV1+u3ft+qpVbv1bwun6sp5YxjKBgAYNPQ8AgAAx+WdLfv0\ns5fWa9m2Zo0pydZNC6fq0tmj+AILpMnKHc364fNrtWJ7s6ZV5uv7F8/Q/KnlTscCAGSQVHseUTwC\nAADHZOmWfbrrlQ16Z0uTKvL9+pdPTNHn5o3hNOKAA6y1WrymTncuXqft+zp02oQSffO8SZo/tZze\nfwCAPlE8AgAAAyYYieqFD/bo4be3a+WO/SrP9+sb8yfpC6ePVZbX7XQ8YMQLRWJ6dOl23ffmFu1p\n6dKM6gJ99ezx+uSsauZEAgAkRfEIAAD0SzRmtWJ7s/62Zo+eWbVb+wIhTSjL1ZfOHKfPn0bRCBiK\nQpGYnl5Vq/ve3KJNe9uV43NrwYxKLaip1NmTSlWa53c6IgBgCKF4BAAAjom1Vtv2dWjZ1iYt3dqk\nNzc2qKEtKJ/HpfOmluuaM8fp7EllcjGnETDkWRsv/v55+S69vLZeTYGQJGlMSbZmjy7S9Kp8jS3N\n1biSHI0tyVFRjpdhbgAwAlE8AgAAScViVtubOrRuT6vW7mnV2ro2rdq5Xw1tQUlSSa5PZ04s1YUn\nVun86RXKY9gLkLGiMatVO/drxfYmrdq5X+/vbFHt/s6DtsnP8mh8aa7Gl+VqQmmOJpTnanxpriaW\n5akwx+tQcgDAYEu1eMSRIAAAw5i1Vo3tIW1uaNeG+rZ4oWhPm9bXtakzHJUkuV1GE8tydc7kMp06\nvkSnTSjWpPI8eiEAw4TbZTR3XLHmjivuWdcRimhnU6e27wtoR1OHdjR1aNu+Dr2/c7+eX71bsV6/\nL5fk+jSxLFcTynI1sTxPE8pyNaYkW6W5fhXleBnCCgAjAD2PAADIcKFITHvbulTfGlR9a5e27Qto\n896ANje0a0tDu1q7Ij3bFuV4NaOqQDOqCzS9Ol811QWaXJHHlz8APYKRqHY2dWprY0BbG9u1tTGg\nzQ0BbW0M9PRO7C3X51ZRjk+5frdy/R7l+T3K9XkSy/F13evzszyqyM9SVaFflQVZys+iVxMAOGlI\n9zwyxiyS9AtJbkm/s9be6UQOAMDwEI7GtL8jrOaOkJoDITV3L3eEtL8jrEAwomAkplDiIklej0te\nt5HP7VK2z62ibJ+Kc70qyvGpKNur4hyfinK8ys+Kf+HxuFM/DX0oElMgGFF7MKJAKJJYjvas6whG\nFAhF4/d3bxeMKBCMKhCKKBK1isasYjZ+HY1ZRRPLsV7L0ZhVJGbV1qs41K2ywK9J5Xm6bM4oTSrP\n1aSKPE2pyFdlgZ8eRQCOyu9xa3JFniZX5EmqPOi+1q6wtjUGVNvc2fNZ2xQ48FkbCMU/0+pbuxQI\nHvici8SO/IN1rs+tqsIsVRVmqbIgS1UFhy+X5fnlHoS51sLRmDpCUXWGouoIRdQRiiYuEXWGogqE\nourstb4zHP8cj8as/B6X/F63/J74PqQs16/SPJ9K8/wqy/OpIj9LPk/q+w0AGOrSXjwyxrgl3SNp\noaRdkpYZY56x1n6U7iwAcCysteoKxw46wAyEIuoIHn7Q2RGKqiscldtl5HG55HEbeVxGXrdLWV63\ncnxuZXndyvbFl7O97p712Yn1fo9rxH3Jt9aqtSuilo6w9nfGv4zs7wyrpeNAQWh/RzjxRSWxLhBS\nW/Dw4kk3n8elfL9Hfo9LvsTFyCgciykcjSkcsQoEI0d9DknK8bmVn+VRjs8jYySXMTKSrKSucDRx\niakzHFU0yZekQ3ndJv6LvC/xS73frVyfR163kdtl5DJGHnf82u0ychsjlyv+f8mVuO12GRXleFVV\nEP+yVVmQpTEl2fyaD2BQFGR5ddLoIp00uijlx1hrFUwU1Vu74oWl+tYu1bV0qa7X8tItTapv7Tqs\n0OQyUpbXLZ/HFS/aeOLLPrdLbpeRMZKRpMTncu/P6HDMKhiOKhiJHbiOxBSMRBWOHtsIjOzEftrt\nMgpFYwqG48+T7CO/JNeX+Fz2q6ogSxWJglhlgb/n87o018dJCABkBCd6Hp0maZO1doskGWMek3SZ\npGFdPNqxr0M/Xryuz+2sUtuJpTraMOXtUnjd1J8rxe1S3l8P3HuSerYUXzPl50txu5Sea2CHmg7k\n/5FUn8+J14w/X2qiMavOULSnINCZuHSFYyk+Q5zbZVIuIhyJMQcOVLO87oOXfW55eg42Tc/2ptdj\n4/eYA8u91knx99faA+9fz+3Ec8TX2173x///Wemwder1GNv7Mfbw55WVYokvEp3haM973f0+H+3f\nM8/vUVGOVyW5PhXl+DS+LFfFOb74Jdfbs1yU41Vxrk8lOT5l+1IbjhWOxtTSGT6oKNXSGVZbVyRx\niS93hKOKJf6gmLUyiS813f9G8UKg66BhGgcN3UgM5cj1u+X3MFQMwPBnjOn5nCzN82tCWW7SbWMx\nq8ZAUPUtQdW1xotLDa1d6kwUfkK9ij+hSEzR2IH9Uu99kk18Rue6XfLn+3t6Cfk9rp5CVPd+Ncfn\nif9444sX8Lt/2DnoPq87aZGnMxTVvkBQje0h7WsPqqEtGB9G3Nal+pYu1bd16cPdrWpsDx62j3MZ\n9bxGPIOnp0DV/QNB/McC9fyo0F0wGyxGg/rkwLBQke/XbZ+a6XSMtHKieDRK0s5et3dJOv3QjYwx\n10u6XpLGjh2bnmSDqCsS1fr6tpS2TfUzNdWdRqo7gIHcCaXaW2LA/9YUthvo9yPlt20A35OBzubE\nv1fKByYDuFn3r5F98XpdKk5MANrdIyg7UbTJ8rqU23OQ51GO360cb7wocOhBp9ftkrVWMRsvTERj\nVuForKf3UmeiONXdZb67kNJdROlMsr4jFFVTIBQ/YE5SxJEOFG66l7u3U2Jb0+sXWtOrABW/Nge9\nZ4cWo0yvjQ88x4HH9n6vjeJ39qwzkse4VJDt7Xl/s7yunh5XhdleFWbHh48V53hVlONVYbZPhdne\nQR0C4HW7VJbnV1mef9BeAwBwdC6XUUV+liryszRLhU7HSUm2z63RvhyNLs456nbhaEyN7UHVtcTn\nqNvb1qWGtqACB/Vgjh8fRKJWkVhMwYhV1MaLar2HMw+WwZwNNxPm2gVS1d519PY+HA3Zs61Za++X\ndL8UnzDb4Tj9NrUyX6/cNN/pGADSzJjuXwvpYQIAwEjmdbtUXZit6sJsp6MAwDFzYha3Wkljet0e\nnVgHAAAAAACAIcaJ4tEySVOMMROMMT5JV0l6xoEcAAAAAAAA6EPah61ZayPGmG9LelGSW9KD1toP\n050DAAAAAAAAfXNkziNr7QuSXnDitQEAAAAAAJA6J4atAQAAAAAAIENQPAIAAAAAAEBSFI8AAAAA\nAACQFMUjAAAAAAAAJEXxCAAAAAAAAElRPAIAAAAAAEBSFI8AAAAAAACQFMUjAAAAAAAAJEXxCAAA\nAAAAAElRPAIAAAAAAEBSFI8AAAAAAACQFMUjAAAAAAAAJEXxCAAAAAAAAElRPAIAAAAAAEBSFI8A\nAAAAAACQFMUjAAAAAAAAJEXxCAAAAAAAAElRPAIAAAAAAEBSFI8AAAAAAACQlLHWOp2hT8aYBknb\nnc4BJFEmqdHpEMAIQFsD0of2BqQP7Q1IH9rb4cZZa8v72igjikfAUGaMWW6tned0DmC4o60B6UN7\nA9KH9gakD+3t+DFsDQAAAAAAAElRPAIAAAAAAEBSFI+A/rvf6QDACEFbA9KH9gakD+0NSB/a23Fi\nziMAAAAAAAAkRc8jAAAAAAAAJEXxCEiBMabEGPOyMWZj4ro4yXaLjTH7jTHPHbJ+gjFmqTFmkzHm\nT8YYX3qSA5nlGNratYltNhpjru21/nVjzHpjzKrEpSJ96YHMYIxZlGgnm4wxtxzhfn9iX7Upse8a\n3+u+f0+sX2+MuTCduYFMdLztzRgz3hjT2Wt/9pt0ZwcySQpt7WPGmPeMMRFjzBWH3HfE40ocjOIR\nkJpbJC2x1k6RtCRx+0h+IumaI6z/saS7rLWTJTVLum5QUgKZr8+2ZowpkXSbpNMlnSbptkOKTFdb\na+ckLnvTERrIFMYYt6R7JF0kqUbS540xNYdsdp2k5sQ+6y7F92FKbHeVpJmSFkm6N/F8AI6gP+0t\nYXOv/dkNaQkNZKAU29oOSV+W9Oghj+3ruBIJFI+A1Fwm6Q+J5T9I+vSRNrLWLpHU1nudMcZIOl/S\nE309HkBKbe1CSS9ba5ustc2SXlb8iyyAvp0maZO1dou1NiTpMcXbXW+92+ETkj6R2JddJukxa23Q\nWrtV0qbE8wE4sv60NwCp67OtWWu3WWtXS4od8liOK1NE8QhITaW1dk9iuU5S5TE8tlTSfmttJHF7\nl6RRAxkOGEZSaWujJO3sdfvQNvX7RBf/WzkABw7TV/s5aJvEvqtF8X1ZKo8FcEB/2pskTTDGrDTG\nvGGMOXewwwIZrD/7J/ZtKfI4HQAYKowxr0iqOsJd/6v3DWutNcZwmkLgOA1yW7vaWltrjMmX9KTi\nw0gfPr6kAAA4Zo+ksdbafcaYuZKeMsbMtNa2Oh0MwMhE8QhIsNYuSHafMabeGFNtrd1jjKmWdCzz\nqOyTVGSM8SR+URotqbafcYGMNQBtrVbSeb1uj5b0euK5axPXbcaYRxXvxkzxCDigVtKYXrePtE/q\n3maXMcYjqVDxfVkqjwVwwHG3N2utlRSUJGvtCmPMZklTJS0f9NRA5unP/inpcSUOxrA1IDXPSOqe\nef9aSU+n+sDEzv81Sd2z+h/T44ERJpW29qKkC4wxxYkJDS+Q9KIxxmOMKZMkY4xX0iWS1qQhM5BJ\nlkmakjgLqE/xCbCfOWSb3u3wCkmvJvZlz0i6KnF2qAmSpkh6N025gUx03O3NGFPePSG9MWai4u1t\nS5pyA5kmlbaWzBGPKwcpZ0ajeASk5k5JC40xGyUtSNyWMWaeMeZ33RsZY/4u6c+KT3a4q9dpjG+W\ndJMxZpPi49gfSGt6IHP02dastU2S7lD8QGGZpP9IrPMrXkRaLWmV4r8k/Tb9fwIwdCV6wH5b8QPj\ntZIet9Z+aIz5D2PMpYnNHpBUmthn3aTEWQ+ttR9KelzSR5IWS/qWtTaa7r8ByBT9aW+SPiZptTFm\nleITad+Q2NcBOEQqbc0Yc6oxZpekKyXdZ4z5MPHYZMeVOISJ/5AEAAAAAAAAHI6eRwAAAAAAAEiK\n4hEAAAAAAACSongEAAAAAACApCgeAQAAAAAAICmKRwAAAAAAAEiK4hEAAAAAAACSongEAAAAAACA\npCgeAQAAAAAAIKn/D98l76PR+IfvAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize = (20,10))\n",
+ "spy.log_return.plot.density()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAD8CAYAAACYebj1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl4lOW5+PHvPVv2sIRgMGHfERA0UteKIgouoNYF1Kq1\nFq1Lq+3PivXosbYerVarPdJjFa2gUtdWsUVxKdW6VAREEBAIeyCBsGed9fn9MQuTZJJMJnmTTHJ/\nrosrM+/7vO/cGZK58+xijEEppZQCsLV3AEoppToOTQpKKaUiNCkopZSK0KSglFIqQpOCUkqpCE0K\nSimlIjQpKKWUitCkoJRSKkKTglJKqQhHewfQXL169TIDBgxo7zCUUiqpLF++fK8xJrepckmXFAYM\nGMCyZcvaOwyllEoqIrItnnLafKSUUipCk4JSSqkITQpKKaUikq5PQSnVfrxeL8XFxdTU1LR3KKoB\nqampFBQU4HQ6E7re0qQgIlOAJwA7MNcY81Cd8/2AeUD3UJnZxphFVsaklEpccXExWVlZDBgwABFp\n73BUHcYY9u3bR3FxMQMHDkzoHpY1H4mIHZgDTAVGATNFZFSdYv8FvGqMGQ/MAP5oVTxKqZarqakh\nJydHE0IHJSLk5OS0qCZnZZ/CBKDIGLPZGOMBXgam1yljgOzQ427ALgvjUUq1Ak0IHVtL/3+sTAr5\nwI6o58WhY9HuA64SkWJgEXBrrBuJyCwRWSYiy8rKyqyIVakWKS4v5sNtH7Z3GEq1WHuPPpoJPG+M\nKQDOBV4QkXoxGWOeNsYUGmMKc3ObnJCnVJv76ZKfctu/bmNv9d72DkUl4N1332X48OEMGTKEhx56\nqOkLLHDHHXcwYsQIxo4dy0UXXcTBgwfbJQ4rk8JOoG/U84LQsWg/BF4FMMZ8DqQCvSyMSSlLbDiw\nAYBth+OaNKo6EL/fz80338w777zD2rVr+ctf/sLatWvbPI7JkyfzzTffsGrVKoYNG8aDDz7Y5jGA\ntUnhS2CoiAwUERfBjuSFdcpsByYBiMhIgklB24dUUjHGRB7vqtBuMStt3bqV0aNHR57/7ne/4777\n7mvRPZcuXcqQIUMYNGgQLpeLGTNm8NZbbzV6zTfffMOECRMYPnw4drsdEWlxDePss8/G4QgOCD3x\nxBMpLi5u0f0SZdmQVGOMT0RuARYTHG76nDFmjYjcDywzxiwEfg48IyK3E+x0vtZE/4YplQQOew5H\nHu+v2d+OkbStX729hrW7DjddsBlGHZ3Nf19wTIvv89JLL/HII4/UOz5kyBBef/31Wsd27txJ375H\nGjUKCgr44osvGr3/7bffzm233cYVV1zBSy+9xGuvvcbs2bNrlSkvL+e0006Lef2CBQsYNaruYMwj\nnnvuOS6//PJGY7CKpfMUQnMOFtU5dm/U47XAKVbGoJTVyqqOVG4PuQ+1YyQq7Morr+TKK6+07P7L\nly/nnXfeAeDyyy/n1lvrj5HJyspi5cqVzb73Aw88gMPhsDT+xuiMZqVaaE/1nsjj6FpDZ9caf9En\nIroxwev1xizTnJpCfn4+O3YcGShZXFxMfn7dgZK12e32SByBQCDS7BMtkZrC888/z9///nc+/PDD\ndhv6q0lBqRYKjziyiU1rCm1g27ZtlJWVkZOTw8cff0xhYWG9Ms2pKZxwwgls3LiRLVu2kJ+fz8sv\nv8yCBQsAuOuuu5gwYQIXXXRRrWsmTpzIggULuOaaa3jxxRdjfvg3t6bw7rvv8vDDD/PRRx+Rnp4e\n93Wtrb2HpCqV9PZUBWsKg7sP1qTQBnJycrj66qspLCxk9OjRzJ8/n02bNiV8P4fDwZNPPsk555zD\nyJEjueyyyzjmmGAtaPXq1eTl5dW75vHHH+fFF19k7NixLFiwgCeeeCLh1w+75ZZbKC8vZ/LkyYwb\nN44bb7yxxfdMhNYUlGqhvdV7yXJmkZeep/MU2kBWVlakPR+I2UzUXOeeey7nnntuveNer5eTTjqp\n3vH8/Hzef//9Fr9utKKiola9X6K0pqBUC+2p2kOv9F5kubK6VJ9CV7B48eL2DqHNaVJQqoX2Vu8l\nNy2XTGcmVd6q9g6nUxswYADffPNNe4fRqWlSUKqFDrsP0y2lGxnODCq9le0djlItoklBqRY67DlM\ntiubdGc6noAHbyD2MEmlkoEmBaVaqNxTTrYrmwxnBoA2IamkpklBqRbw+D3U+GvIcmVFkoI2Ialk\npklBqRYo95QDkOXKIt0ZnHCkSSH5dISls++55x7Gjh3LuHHjOPvss9m1q30WV9SkoFQLhIegZrmy\nyHBoTSEZdZSls++44w5WrVrFypUrOf/887n//vvbPAbQpKBUi0TXFDJdmYD2KVipMy+dnZ2dHXlc\nWVmpax8plYyqfdUApDvSSXeEmo98XaSm8M5sKF3duvfMGwNTW958k6xLZ999993Mnz+fbt26sWTJ\nkkZjsIomBaVawO13A5BiT9GO5g4kWZfOfuCBB3jggQd48MEHefLJJ/nVr37VKvE2hyYFpVogkhQc\nXTAptMJf9InozEtnh1155ZWce+65nS8piMgU4AmCO6/NNcY8VOf874EzQk/Tgd7GmO5WxqRUa4qu\nKYRHH4WblJQ1OuvS2Rs3bmTo0KEAvPXWW4wYMSLua1uTZUlBROzAHGAyUAx8KSILQ7utAWCMuT2q\n/K3AeKviUcoKbt+RpOCyuRCEGl9NO0fVuYWXzt69ezeTJk1i/vz5XHvttQwePDih+0Uvne33+7nu\nuutqLZ09bdq0etc8/vjjXHvttTz66KP07t2b559/viXfEgCzZ89m/fr12Gw2+vfvz1NPPdXieybC\nyprCBKDIGLMZQEReBqYDDY31mgn8t4XxKNXqomsKIkKqI1WTgsU669LZb7zxRqveL1FWDknNB3ZE\nPS8OHatHRPoDA4F/NnB+logsE5FlZWVlsYoo1S6ikwJAqj2VGr8mhc5Cl85uPzOA140x/lgnjTFP\nG2MKjTGFubm5bRyaUg2rlxS0pmApXTrbelYmhZ1A36jnBaFjscwA/mJhLEpZwu1347A5sNvsQCgp\naE1BJTErk8KXwFARGSgiLoIf/AvrFhKREUAP4HMLY1HKEm6/O1JLgFDzkdYUVBKzLCkYY3zALcBi\nYB3wqjFmjYjcLyLR3fkzgJdN9OBjpZKE21cnKWjzkUpyls5TMMYsAhbVOXZvnef3WRmDUlaq8dfU\nqylU+XTtI5W8OkpHs1JJyeP3aE2hE+gIS2fv37+fyZMnM3ToUCZPnsyBAwdilrPb7YwbN45x48bF\nnEPRUpoUlGqBWDUF7WhOLh1l6eyHHnqISZMmsXHjRiZNmtRgckpLS2PlypWsXLmShQvrddO2mCYF\npVrA4/eQ4qhdU9BlLqzTmZfOfuutt7jmmmsAuOaaa3jzzTdbdL9E6YJ4SrVAja+mXvNReO5CZ/fb\npb/l2/3ftuo9R/QcwZ0T7mzxfZJx6ezdu3fTp08fAPLy8ti9e3fMa2tqaigsLMThcDB79mwuvPDC\nRmNtLk0KSrWAx++hu/PIGo7ap9AxJOvS2WEi0uAmO9u2bSM/P5/Nmzdz5plnMmbMmITXfYpFk4JS\nLRCrT8HtdxMwAWzSuVtnW+Mv+kR01qWzjzrqKEpKSujTpw8lJSX07t075rXh2AYNGsTEiRP56quv\nNCko1VHEGn0EwWal8FLaqnV11qWzp02bxrx585g9ezbz5s1j+vTp9cocOHCA9PR0UlJS2Lt3L59+\n+im/+MUv4n6NeHTuP2WUsljdmkL4scfvaa+QOr3w0tmFhYWMHj2a+fPns2nTpoTvF7109siRI7ns\nsstqLZ2dl5dX75rHH3+cF198kbFjx7JgwQKeeOKJhF8/bPbs2bz//vsMHTqUDz74INJHsWzZMq6/\n/noA1q1bR2FhIcceeyxnnHEGs2fPbnSznkRoTUGpFqhbU3DanMHjAU0KVumsS2fn5OTw4Ycf1jte\nWFjI3LlzATj55JNZvbqV98WuQ2sKSrVA3bWPXHYXoDWFzkKXzlZKxc0YE0wKUfMUXLZQUtCagiV0\n6WzraVJQKkG+gI+ACcSsKXj9sUfFKNXRaVJQKkF1N9gBbT5SyU+TglIJCq9xpB3NqjPRpKBUgsK1\nAa0pqM7E0qQgIlNEZL2IFInI7AbKXCYia0VkjYgssDIepVpTrJpCuKPZG9A+hWT10ksvMXbsWMaM\nGcPJJ5/M119/3S5x3H333fTt25fMzMw2fV3LkoKI2IE5wFRgFDBTREbVKTMUuAs4xRhzDHCbVfEo\n1doiNQWH1hQ6k4EDB/LRRx+xevVq7rnnHmbNmtUucVxwwQUsXbq0zV/XyprCBKDIGLPZGOMBXgbq\nztv+ETDHGHMAwBizx8J4lGpV4YXvavUp2EN9CpoULGHF0tl1nXzyyfTo0QOAE088keLi4iavee21\n1xg5ciQDBgyILGb3n//8p0VxnHjiiZFVU9uSlTOa84EdUc+Lge/UKTMMQEQ+BezAfcaYdy2MSalW\nE7NPoQs1H5X+z//gXte6S2enjBxB3i9/2eL7NGdBvMY8++yzTJ06tdEylZWV3HrrrXz22WcMGjSI\nH/3oRxxzzDGceOKJtcotWbKE22+/vd716enpfPbZZ3HHZLX2XubCAQwFJgIFwMciMsYYczC6kIjM\nAmYB9OvXr61jVCqmmH0Kdp281hG0xtLZS5Ys4dlnn+WTTz5ptNyGDRsYPnw4gwYNAmDmzJk88cQT\n3HZb7dbwM844I+GltNuSlUlhJ9A36nlB6Fi0YuALY4wX2CIiGwgmiS+jCxljngaeBigsLDQo1QHE\nnKdg6zp9Cq3xF30iWnvp7Dlz5vDMM88AsGjRIo4++mhWrVrF9ddfzzvvvENOTk6j8TgcDgKBQOR5\nQ0tpa00h+ME+VEQGEkwGM4Ar6pR5E5gJ/FlEehFsTtpsYUxKtZpwUggvlw06o7kttPbS2TfffDM3\n33xz5Pn27du5+OKLeeGFFxg2bFitspMmTWL+/Pm19lsYPnw4O3fuZMOGDQwbNoz58+czceLEeq+T\nLDUFyzqajTE+4BZgMbAOeNUYs0ZE7heRaaFii4F9IrIWWALcYYzZZ1VMSrUmt69+TSHS0azNR5Zp\n7aWz67r//vvZt28fN910E+PGjYsknUAgQFFRET179qxV3uVyMW/ePGbMmMGYMWNwuVzccMMNLY7j\nF7/4BQUFBVRVVVFQUNDqHeoNsbRPwRizCFhU59i9UY8N8LPQP6WSSqzmI4c4EKRLNB+1FyuWzo42\nd+7cyFLV0dauXcv3vvc90tLS6p077bTTWLFiRavG8fDDD/Pwww+36j3joTOalUpQrKQgIjhtTq0p\ndEKjR4/msccea+8wLKdJQakEhZNCuB8hzGV3aZ+CRXTpbOtpUlAqQW6/G4c4cNhqt8K67K5O3XwU\nPfpHdTwt/f/RpKBUgupusBPWmZuPUlNT2bdvnyaGDsoYw759+0hNTW26cAPae/KaUknL7au9FWdY\nZ64pFBQUUFxcTFlZWXuHohqQmppKQUFBwtdrUlAqQXX3Zw5z2VyddpkLp9PJwIED2zsMZSFtPlIq\nQQ0mhU5cU1CdnyYFpRKkSUF1RpoUlEpQo0mhk3Y0q85Pk4JSCWpo9JHLpvMUVPLSpKBUgtw+d72J\naxCsKYQntimVbDQpKJUgd8BNqr3+eHBtPlLJTJOCUglqsKZg045mlbw0KSiVILe/kZqCJgWVpDQp\nKJUgtz92TaEzL3OhOj9NCkolqKGaQoo9RWsKKmlZmhREZIqIrBeRIhGZHeP8tSJSJiIrQ/+utzIe\npVqLMabBmoIuna2SmWVrH4mIHZgDTAaKgS9FZKExZm2doq8YY26xKg6lrOAL+AiYQK39mcOcdic+\n48Mf8GO32dshOqUSZ2VNYQJQZIzZbIzxAC8D0y18PaXaTKxd18JctmDtQfsVVDKyMinkAzuinheH\njtX1PRFZJSKvi0hfC+NRqtXU+GuA2EkhfEz7FVQyau+O5reBAcaYscD7wLxYhURklogsE5Fluo67\n6gjCH/gNrX0EdNrls1XnZmVS2AlE/+VfEDoWYYzZZ4wJrwcwFzg+1o2MMU8bYwqNMYW5ubmWBKtU\nczRWU3DanAC61IVKSlYmhS+BoSIyUERcwAxgYXQBEekT9XQasM7CeJRqNfHUFLT5SCUjy0YfGWN8\nInILsBiwA88ZY9aIyP3AMmPMQuAnIjIN8AH7gWutikep1lTjC9UUYq2SqklBJTFLt+M0xiwCFtU5\ndm/U47uAu6yMQSkrNFZTCB/TPgWVjNq7o1mppKR9Cqqz0qSgVAK0T0F1VpoUlEpAYzWF8OQ1bT5S\nySiupCAifxWR80REk4hSxFdT0OYjlYzi/ZD/I3AFsFFEHhKR4RbGpFSHp6OPVGcVV1IwxnxgjLkS\nOA7YCnwgIp+JyA9ExGllgEp1RNqnoDqruJuDRCSH4DyC64GvgCcIJon3LYlMqQ5M+xRUZxXXPAUR\n+RswHHgBuMAYUxI69YqILLMqOKU6Ko/fg13sOGz1f4W0T0Els3gnrz0TmogWISIpxhi3MabQgriU\n6tBq/DUxawlwpPagSUElo3ibj34T49jnrRmIUsnE4/doUlCdUqM1BRHJI7gHQpqIjAckdCobSLc4\nNqU6rBpfTcytOAFEhBR7iiYFlZSaaj46h2DncgHwWNTxcuCXFsWkVIfn8XtibsUZ5rK7cPs0Kajk\n02hSMMbMA+aJyPeMMW+0UUxKdXhuv7vB5iOAVHuq1hRUUmqq+egqY8yLwAAR+Vnd88aYx2JcplSn\n11RScNldmhRUUmqq+Sgj9DXT6kCUSiZuv7vBPgXQmoJKXk01H/0p9PVXbROOUsnB7XeT7cpu8LzW\nFFSyindBvIdFJFtEnCLyoYiUichVcVw3RUTWi0iRiMxupNz3RMSIiM55UEmhyZqCI1U7mlVSinee\nwtnGmMPA+QTXPhoC3NHYBSJiB+YAU4FRwEwRGRWjXBbwU+CL+MNWqn01Nk8BtKagkle8SSHczHQe\n8Jox5lAc10wAiowxm40xHuBlYHqMcr8GfgvUxBmLUpbx7dtH1fLlGGMaLdfYjGbQPgWVvOJNCn8X\nkW+B44EPRSSXpj/E84EdUc+LQ8ciROQ4oK8x5h9xxqGUZYzXy9aZV7Dtyqs4+MqrjZbVmoLqrOJd\nOns2cDJQaIzxApXE/qs/bqENex4Dfh5H2VkiskxElpWVlbXkZZVqUMVHH+Hdvh2AfXPnNlpbcPvd\nMfdSCNOagkpWzdlJbQRwuYhcDVwCnN1E+Z1A36jnBaFjYVnAaOBfIrIVOBFYGKuz2RjztDGm0BhT\nmJub24yQlYpfxSefYMvIIO++/8ZbXIx748YGy7p9jc9TSHGkRDbiUSqZxDv66AXgd8CpwAmhf02N\nFPoSGCoiA0XEBcwAFoZPGmMOGWN6GWMGGGMGAP8BphljdClu1S4qP/2M9BNPJHPixMjzWHwBHz7j\na3T0UYo9RTfZUUkp3qWzC4FRpqnetyjGGJ+I3AIsBuzAc8aYNSJyP7DMGLOw8Tso1Xa8JSV4d+yg\n5/e/jzMvD0efPtSsWROzbPjDPtXe8NpHKfaUyEY8SiWTeJPCN0AeUNJUwWihPRgW1Tl2bwNlJzbn\n3kq1pqoVKwBIO/44AFJHjKBm3bqYZcN9BU3VFLwBLwETwCbNaaVVqn3FmxR6AWtFZCkQ6T0zxkyz\nJCql2lj1iq+Q9HRShw8HIHXkSCo++ohAdTW2tLRaZcNJodE+hag9FdIcaQ2WU6qjiTcp3GdlEEq1\nt6qvVpB27FjEEfyVSBk2FAIBPNu2kTpiRK2y4eajeJKCx+/RpKCSSrxDUj8iOJPZGXr8JbDCwriU\najP+ikrc364nffz4yDFXv34AeLZuq1c+3FfQ1OgjQEcgqaQT7+ijHwGvA38KHcoH3rQqKKXaUs2q\nryEQIG38cZFjzn79AfCE5i1Ea25NQalkEm8P2M3AKcBhAGPMRqC3VUEp1ZaqVnwFIqSNOzZyzJ6Z\ngb1XLzzb69cUIn0KjUxeCycFHYGkkk28ScEdWr8IABFxAHEPT1WqI6tesYKUYcOwZ2XVOu7q3x9v\njOaj8OqnTa19BFpTUMkn3qTwkYj8EkgTkcnAa8Db1oWlVNswfj/VX39N2vhx9c65+vXDs63hmkJj\nQ1LD57SmoJJNvElhNlAGrAZuIDj34L+sCkqptuIu2kSgspK0cTGSQv/++MrKCFRW1r4mlBQam7yW\n6gie0z0VVLKJa0iqMSYgIm8CbxpjdEU61WlUr1wJUGvkUZhrwJHO5tSRIyPHm1NT0EXxVLJptKYg\nQfeJyF5gPbA+tOtazFnJSiWb6pUrsffogTM0BDWaq38oKdRpQopn8lq4FqFJQSWbppqPbic46ugE\nY0xPY0xP4DvAKSJyu+XRKWWx6q+/Jm3cOESk3rmG5irEkxTCNQVPQDuaVXJpKil8H5hpjNkSPmCM\n2QxcBVxtZWBKWS3gduPZupXUkSNinrdlZODIzU2ophC9zIVSyaSppOA0xuytezDUr+C0JiSl2oZn\nyxYIBEgZMqTBMq7+/eslBZ28pjqzppJCYz/R+tOukpp7YxEArsENJwXngPpJocZfg8vmitnkFKYd\nzSpZNTX66FgRORzjuAANj8dTKgm4NxWB3Y5r4IAGy6QMGMChffvwHz6MPTsbaHp/ZgCXTZOCSk6N\nJgVjjL2tAlGqrXk2bcLVrx82VyNDSwcNBsC9aVNk2GpT+zMD2G12HDaHNh+ppGPp7h8iMkVE1otI\nkYjMjnH+RhFZLSIrReQTERllZTxKRfPu3IWzoKDRMilDg01L7qKiyLGm9meOXGtP0ZqCSjqWJQUR\nsQNzgKnAKGBmjA/9BcaYMcaYccDDwGNWxaNUXd7SUpx9+jRaxpmfj6Sm4inaFDnm9rsbnbgWpvs0\nq2RkZU1hAlBkjNkcWkzvZWB6dAFjTHR/RQa6yJ5qI4GaGvz79+Psk9doObHZSBk0qFZNweP3NLrE\nRZjL7tKagko68e68loh8YEfU82KCE99qEZGbgZ8BLuBMC+NRKsJXWgqAI6/xmgKAa8hgqpZ+GXle\n46+Jq6bgsmlSUMmn3XcUN8bMMcYMBu6kgUX2RGSWiCwTkWVlZbr0kmo5bygpNFVTAEgZPARfaSn+\n8nIgvtFHEKwpaPORSjZWJoWdQN+o5wWhYw15Gbgw1gljzNPGmEJjTGFubm4rhqi6Km9JKCnkxZEU\nQp3Nnk3BfgW3XzuaVedlZVL4EhgqIgNFxAXMABZGFxCRoVFPzwM2WhiPUhG+0hIAHPEkhcGhYamh\nfoXmJAWtKahkY1mfgjHGJyK3AIsBO/CcMWaNiNwPLDPGLARuEZGzAC9wALjGqniUiubdVYK9Z09s\nqU13GDsLCpCUFNxFR2oKcfUp2F1U+6pbHKtSbcnKjmaMMYsIbsgTfezeqMc/tfL1lWqIt7Q0rqYj\nALHbcQ0ahDvcfORzRzbRaUyKPYVD7kMtilOpttbuHc1KtQdfaQmOJuYoREsZMuRI81HAHVnGojE6\nJFUlI00KqkvylsRfU4Bgv4KvpAR/RUXco4+0o1klI00Kqsvxl5cTqKjAeXQzagpRy13U+GqaXPsI\ntKNZJSdNCqrL8ZbEP/IoLDwCqbpoIwYT/zwF3XlNJRlNCqrL8UUmrsVfU3D27Yu4XFRvWA80vsFO\nmNYUVDLSpKC6nOZMXAsTux1n3764i4Mrt8RbU3D73RijS3qp5KFJQXU53tISsNlw9O7drOucffrg\nL90NxF9TCJgAPuNLKE6l2oMmBdXl+EpKcfTujTiaN03H2acP/pLmJQXQfZpVctGkoLqc5kxci+bo\nkwcHDuL0mbgmr+k+zSoZaVJQXY6vpCT4Ad9Mzj5HA9DzMHHtp6A1BZWMNCmoLsUYE6wpHJVIUghe\n06tcawqq89KkoLoU/8GDGLc7rn0U6goPYc05TNyT10CTgkoumhRUl+KLTFyLf45CWHiyW6/DkGZP\na7K8Nh+pZKRJQXUp3tCQ0kRqCraUFHzdM+h12MRVU3DanADU+Gqa/VpKtRdNCqpL8TZjc51YPDnZ\n9CyPr6M5zRGsTeieCiqZaFJQXYqvpBQcDhy9eiV0fU3PTHrG2dGc4cwAoNJXmdBrKdUeLE0KIjJF\nRNaLSJGIzI5x/mcislZEVonIhyLS38p4lPKWluLs3RuxJfajX90jNdjRHMfktXBSqPZqTUElD8uS\ngojYgTnAVGAUMFNERtUp9hVQaIwZC7wOPGxVPEpBeI5C8zuZwyq7p5FVAza3N3Ks2uNn58Fq3D5/\nrbKRmoJXawoqeVi5HecEoMgYsxlARF4GpgNrwwWMMUuiyv8HuMrCeJTCW1pK2rHHJnx9eY/g3APf\n7t2Ygr48uOhbFizdjscXwGETzhzRm19MGcGQ3pmkO9MBTQoquVjZfJQP7Ih6Xhw61pAfAu/EOiEi\ns0RkmYgsKysra8UQVVdiAgF8u3cnNPIo7HB28O8oT2kps99YzfOfbeWicfk8ePEYrjl5AF9s2c+5\nf/g3760pxWlz4rK5tE9BJRUrawpxE5GrgELg9FjnjTFPA08DFBYW6jrEKiH+/fsxXm9CcxTCDnSz\nA7B82Xr+VtyLn00exk8mDY2cv+H0Qfxo/nJuemkFT199POnOdKq8VS2OXam2YmVNYSfQN+p5QehY\nLSJyFnA3MM0Yo1M/lWUi+yi0oKZwICv4K/P5F+sY2juTm88YUut876xUXvzhBEb0yeLWBV/hlDRt\nPlJJxcqk8CUwVEQGiogLmAEsjC4gIuOBPxFMCHssjEWpFs9RAKiwe6hMs2PbW8bPzx6G3Sb1ymSl\nOnn2mhPISnWyrxwOVFck/HpKtTXLkoIxxgfcAiwG1gGvGmPWiMj9IjItVOwRIBN4TURWisjCBm6n\nVIv5Ethxra4ar5u9mQ4GmUrOOabh+xyVncrcawrx+1x8vXM3gYC2eqrkYGmfgjFmEbCozrF7ox6f\nZeXrKxXNu7sUcbmw9+yZ8D12HjrE3nQnY+3ViNSvJUQbnd+Nwb1y2Li3jLmfbGbWdwcn/LpKtRWd\n0ay6DF/bTctZAAAYwElEQVRJKY68vCY/zBtS7fGzu6KC8u5ppB7cF9c1g3vlkJnm57H3N7DroE5i\nUx2fJgXVZSS641rYc59uwW/cuPp0w79vHwFP06ufZjgzyEj1YQw89M63Cb+2Um1Fk4LqMrw7d+I8\n+uiErt1X4eb//rWJFFcAR58eAPj2ND1nJsOZgdtfzazvDmLh17tYueNgQq+vVFvRpKC6hIDbjW/P\nHpx9CxK6/pHF66n2+nE6fHhzugHg213a5HUZzgwqfZXM+u4geqQ7eez9DQm9vlJtRZOC6hK8O3eB\nMbgKmp8UPt5Qxstf7uC6UwZQ469CeucE71nadFLIdmUTMAFsdg83nD6YjzeUsWzr/mbHoFRb0aSg\nugRvcXDFFWffvk2UrO1wjZc731jF4NwMbj6zX/AD/qhcAHyhDXsak+nMBKDcU87VJ/WnV2YKj76n\ntQXVcWlSUF2Cp7gYAGd+82oK97+9lt2Ha3j0snH4CU64T+3WE1tGBt44mo8yXUeSQrrLwU0TB/P5\n5n18VrS3md+BUm1Dk4LqErw7ipGUFBy58W+u8/7a3by+vJibJg5hXN/ukTWMMpwZOPLy4qopZLmy\ngGBSALjiO/3Iy07l0fc3YIxOaFMdjyYF1SV4i4tx5ufHvbmOxxfgvoVrGJGXFVnwLrzaaYYjA+dR\nR8VVU8hyBpNChTe41EWq084tZw5h+bYDfLRBV/xVHY8mBdUleLZuwdU//o39Xl9ezM6D1cyeOgKX\nI/hrEl7YLt2Z3uyawmHP4cixywr7UtAjjce0tqA6IE0KqtMzPh/urdtIGRLfMhMeX4A5S4oY17c7\npw/LjRwPJ4UMZwaOo3rjKyvD+HyN3ivcp1DhObIonsth4ydnDmVV8SE+WKfrQKqOpUPsp6CUlTzb\nd4DXi2twfEnhjRXBWsIDF42utSRGuE8h3YAz1QOBAL5/PIjTVQmeCvBUgt8DNjvYHJDajaxuwdFO\n5e5DtV7j4uPy+eO/ivj9+xs4a2TvhJfeUKq1aVJQnZ57UxEAKXEkBY8vwJP/rFNLCARg67+p/OrP\nAGQ8fSauYgF64Xn3Dzj7pkBKJrgywJ4Cxg9+L1TvJ6X6AK7+fSn//Emo8kPhD8CZhsNu4+YzhnDH\n66tYsn4PZ444yqpvX6lm0aSgOj3Ppk0AuAYOarJsrVoCwNqF8K8HYc9aKnv0hO6ZpJ90Ky7XYPjX\nA3hOfoSM71/b8A0rysh86wLKBVh8Fyx9Gi54AgadzoXj83niw4384cMizhiutQXVMWifgur03EWb\ncBzdB3tmRqPlatUSCuzw6veD/0wALvoTh065FZvYyDrzHhynXIGkpODZ2URnc2Yu2em5VAw8Da5+\nC8QG86fDR4/gFPjxxMGs3HGQT4viW3VVKatZmhREZIqIrBeRIhGZHeP8d0VkhYj4ROQSK2NRXZd7\n8yZSBg9pstwrX25n58Fq7vqOC3l2MmxYDGf9Cm78FI6dwSFfFd1c3bCJDbHZcPXrh2fbtibvm+nM\nDM5TGDQRbvwExlwKS34Dr1/LJcfmkpedyh/+ubHl36hSrcCypCAidmAOMBUYBcwUkVF1im0HrgUW\nWBWH6tqM349n02ZSBjXedFTp9vHEh0VcmV/KhH9eDtX74eqFcOptYA+2sh6oOUC3lG6Ra1wDBsSV\nFLJcWZR7y0MXpcPFT8PZv4G1b5Hy6kxuPiWPpVv288VmrS2o9mdlTWECUGSM2WyM8QAvA9OjCxhj\nthpjVgEBC+NQXZh31y6M242rieGof/50CxOqPuLXB2cjqd3g+g+h/0m1yhxyH6JHao/Ic9eA/nh2\n7IhrWGr0kFRE4ORb4cKnYMu/uXL9rQzI8DLnX5ua/w0q1cqsTAr5wI6o58WhY0q1GffG8MijhpuP\nDlS4cX/0OH90/QHb0ePhhx9ATv0kcsBdv6aA14t3585GY8h2ZUeWuahl3Ey4/AVspat4Ne1BVm3Y\nzOriQ/XLKdWGkqKjWURmicgyEVlWVqZLA6j41Xy7DoCUYcNiF/C52f78dfxcXuTw4GnBJqOMnJhF\nD7oP0iPlSE0hfM+a9esbjSHTmRlZ5qKeEefBzL+QW7OVV1Mf4IUPljbxHSllLSuTwk4gep3igtCx\nZjPGPG2MKTTGFObm5jZ9gVIh7m/X4+zfL/bIo4oyPM+dz7F7/87iXteQfeU8cKbGvI8xhoM1B+me\n0j1yLGXoULDZcH/b+DabWa4sqn3VeAPe2AWGTkaueIWBtj3M2vwTtmzRTmfVfqxMCl8CQ0VkoIi4\ngBnAQgtfT6l6ar79ltQRI+ufKP0GnjkDKVnJT3w/YeTMh6CRxfIqvBV4Ah5y0o7UImypqbgGDaRm\nXeNJIdZSF/UMmkj15a/SR/aTtWA6HNzRcFmlLGRZUjDG+IBbgMXAOuBVY8waEblfRKYBiMgJIlIM\nXAr8SUTWWBWP6nr8FRV4t28ndeSI2ifW/R2ePRufz8ulnnvJOv4y+uWkN3qvPVXBNYp6p/eudTx1\nxEhqmqgphPshDrgPNFoue/jpvDzif3F5DuB7dgrs39JoeaWsYGmfgjFmkTFmmDFmsDHmgdCxe40x\nC0OPvzTGFBhjMowxOcaYY6yMR3Ut7lBbf8qIUFIwBj7+HbxyJeQO54Gj/8g6GcKtZw5t8l67q4KT\n1OolhZEj8JWU4Nvf8BabuWnBJs991U0POT333Av4vu+/8FQdhj+fC3u1KUm1raToaFYqETVr1gKQ\nOnIk+Nzw11nwz1/DmEvZdP4rzPumhqtP6k9et9j9CNEiNYW02kkhbfx4AKpXrGjw2nBSCN+jMX26\npTHyuNO4zP1fBHzuYGLYs67J65RqLZoUVKdVvfIrHH364Mx2wQsXw+pX4cx74OJn+O0H20l3Ofjx\nxKZnOsORD/Tc9NoDHVJHj0ZcLqqWN5wUeqUHd3vbWx3fFpw3nj6Ytf4C5g55MrgsxvPnQcmquK5V\nqqU0KahOq2rFV6QfMwyePQeKl8L3noXv/j+Wbz/Ae2t3c+Ppg+iZ4YrrXnuq9tAtpRupjtq1CpvL\nReqYMVStWN7gtVnOLFLsKZRVxTecekCvDKYdezSPfiWUXvI3cKTBvPNhZ8OvoVRr0aSgOiXvrl34\nSktJq1wCFaXw/b/BmEuo9viZ/cZqjspO4bpTB8Z9vz1Ve+r1J4SlH388NWvWEqiqinleRMhNy2VP\ndfwb6twxJdgP8j+fu+EHiyC1O8ybDtv/E/c9lEqEJgXVKVX+bS4A6flO+OH7MOBUAH7zj7UUlVXw\n6KXjSHfFv3J840nhOPD5qF7VcBNPbnpu3M1HAPnd07jhu4NY+PUulh7Mgh+8A1lHwQsXwerX476P\nUs2lSUF1Psv+TMXf/owj00bKLz6A3OEAvPtNCS99sZ1Z3x3EqUN7NeuWJZUl5KXnxTyXdvzx4HBQ\n+dnnDV7fO713XB3N0W6cOJj87mnc+cYqqtPygomhz7Hwxg/hndnBjXyUamWaFFTnEfDD4rsxb91G\n5Z50Ms+ZjmQHP8h3HazmzjdWM7agGz+fPLxZt63yVrG/Zj8FWQUxz9szM0kbdyyVn3zS4D3yM/PZ\nVbELf8Af9+umuxw8culYtuyt5OHF30Jmb7jmbfjOj+GL/4N5F8DhkmZ9L0o1RZOC6hzcFfDKVfD5\nk1T2vIiAJ0DmpLMA8AcMt7+yEp8/wB9mjMflaN6P/Y7y4OzihpICQOapp1Kzdm2D8xUKsgrwBryU\nVTdv7a6TB/fimpP68+dPt/Jp0V6wO2HqQ8FO85Kv4alTYeMHzbqnUo3RpKCSX9l6eHYybHgXpj5C\n+f6+2NLTyTj5ZAD+uKSIL7bs5/7poxnQq/Hd12IprigGoG9W3wbLZJxyCkCDTUgFmcGEEk4wzTF7\n6kiG9M7ktldWsrfCHTw45hKY9S/IPApe+h68d482J6lWoUlBJbeVC+DpiVCxB658HTP+Wg6/9z6Z\nZ03ClprK8m37efzDjUwfdzQXH5fYyu3F5cGkEP5gjyV11CjsOTmUfxD7r/ZwLSN8r+ZIc9l58orx\nHKr28vNXvyYQMMETucPhRx9C4XXw2R/guSlwoOlNf5RqjCYFlZzcFfDXG+DNH0P+8cFtLodMovLz\nzwkcOkT21KkcrPLwk7+s5OjuqfzmwtGISEIvtaN8B1murFp7KdQldjvZU6ZQsWQJ/or6C9/lZeTh\ntDnZciix9YxG5GVz7/mj+GhDGXM/2XzkhDMNzv89XPo87N0AT50Ga99K6DWUAk0KKhlt+yzYlr7q\nFZh4F1z9FmT3AeDQP/6BLTub9JNO5qcvr2RPeQ1/mDGerFRnwi+39fBW+mf1b7Jc9vnnYdxuyt+v\nX1tw2pyMzBnJ12VfJxzHld/px9TReTz87nq+3nGw9sljLoIbPg5uDvTq1fD3n4En9rwJpRqjSUEl\nD08VvPvL4HpAJgDX/h0mzgabHQDfgQOUv7uY7PPO5ZElW/hoQxn3TTuG8f16NHHjhhlj2LB/A8N6\nNrBJT5S0ceNwDRzI/vnzMcbUOz8+dzyr965ufAntRogID108lqOyU7nlLyuO9C+E9RwI1y0ObvW5\n7Fn43+Ng+bzguk9KxUmTgur4jIFVr8KThfCfOXDCD+HHn0UmpIUdfOUVjMfDokGn8tRHm7jyO/24\nYkK/Fr10WXUZB9wHGNaj6aQgIuTMmoV73TrK33233vkz+52JN+Dl4+KPE46nW7qTJ68YT1m5m6vm\nfsGewzW1CzhccPZv4AfvQrcCePsn8NioYEf0zhXB91KpRmhSUB1XIADr3oZnzoC//ggycoMfduc9\nCimZtYr6ysrY+8xctg0/nl+vqeHi8fn8enri/Qhhy3cH1xsa3Wt0XOW7XXA+qcccQ+l9v8JTXHuj\nwXG9x5Gblst7295rUUzj+/XgmasL2bavinP/8Alvrdx5pPM5rP9JwZncV/0V+p0In88Jvo+/Hx2c\n+Lb10+C8DqXq0KSgOp6KPfDZkzBnQnDuQfUBmD4HfrQk+GFXhwkEWPvT/4enxs2v+57FTycN5XeX\nHovN1rKEALBkxxKyXdmMzokvKYjDwdG/ewRjDDtuuAH/oUORczaxcVb/s/hk5ydUeVvW3n/a0Fze\nvPkUcrNS+OnLKznr9x/x7CdbOFjliQpGYMgkmPES3FEEF/4f9BkLy56D58+FR0cE+x62fAx+X4vi\nUZ2HxGr7bLWbi0wBngDswFxjzEN1zqcA84HjgX3A5caYrY3ds7Cw0CxbtsyagFX7MAb2FcHG92Hj\ne8EPKeMPjio66WYYOR3ssdcp2r6vin/f9WuO+/hNXjx5Juf98iZOHtK8JSwasrd6L2e/fjaXDLuE\nX37nl826tvKLpWy//nrSx4+n79xnsLmCq7EuK13GDxb/gEe++whTBk5pcYyBgOHtVbt4/rOtfLX9\nICkOG+eN6cOVJ/bjuH49YteU3BXB93ntW8Gv3ipI7wUjL4BjLoT+pzb4fqvkJSLLjTGFTZazKimI\niB3YAEwGignu2TzTGLM2qsxNwFhjzI0iMgO4yBhzeWP31aSQxIyB8lI4sCW41WTZt1C6KrhXQHVo\nJnCv4TDiXDh2ZmTNotq3MGzdV8Wyrft5/6vtDHxrPhcWfcy2E8/iu3/6PekprfdhdufHd/Letvf4\n27S/MaDbgGZff+jtv7PrjjvIPv98jn74t4jNhj/g56zXz2J87/E8NvGxVosVYO2uwyxYuo03v9pF\nhdvHkN6ZTDkmjzNG5DI6vxspDnv9izyVwWS89k3YsDiYINJ6Qv+Toe8EKDgB+owDV+PblaqOryMk\nhZOA+4wx54Se3wVgjHkwqsziUJnPRcQBlAK5ppGgNCm0E2Mg4ANfTXA0i7c6+NVXHfxgcZcH/3kq\ngn+JusvBUx58XLEnmAgObA1+6ITZXdB7FCZvLL4+46gqOJ3ytKOp8vipdPsiX/dVeti6t5KNeyrY\nsGkXPUq2cULpOqbsWEaWu4KUSy9n4H33IPYYH3oJKPeUM3/tfJ76+iluGncTPz72xwnfa+9Tf6Ls\n8cdJHTWK7pddSvqECTxR8hdeLHqFOyfcycwRM7FJ67biVrp9LPx6F2+t3MnSLfsJGHDZbYwp6Mb4\nvt0ZlJtJ/5x0ema4yExxkJXqINVpx+Gvxr75Q+TbRbDji+D/GYDNAb2GBZN07gjIGRKcSZ2VB+k5\nwbkSjtRgc5XqsDpCUrgEmGKMuT70/PvAd4wxt0SV+SZUpjj0fFOoTINrDCecFFa8AJ/9b+hJ6Huu\n9b1HPY51vMmyJubpWGUPVXtw+wKAIfrXSKh/r9q/ZlHHQ/cSYv//hY9LPPeKlI193k4AF17sBGK+\nVsnSblTtdYUuCd7FGDBGCCAEsOE3dnzY8GPHb4JfA0jwmqjvRUz4PTHYwsdDxxwYUsLDK+12Mk47\njV4/vI70E06IGRfAC2tf4LUNr2GMIWACBEwAw5HHsY5VeavwGR9TB0zlwdMexG5LPNkYYzj89tvs\nfepPeDYfmXTmtwseuyFgFwJ2G367hP6BaeTDNduVTbfUhifR1RUIGEou+j6f5h/L8m0HWLXzEB5f\n7P9HCH6uO202nHYh11bOOFsRY9nAELOdgaaYfHZja+Bnzo0LL47g/2vopyoQ6rY0wf9djEjkMXXO\n1ysbKR/9s2lN4nHYhfxuaZbcu1VNvBNGfy+hS+NNCknRcCgis4BZAP36JTjEMD0Heo+Mvmn4QYxj\nDR1vomyT1wePl+4uZ1/lkQ7B8C+IhB6L1E8XsX8X6scV/kCJvlf0a9SOK8Y9ar2OLXJPn7jw2Vx4\nJQWfzYXflhI5llOyitSU/fhtDgLiIGBz4Lc5MWKLfO/BuCT4PPz9hY7Z7YLDbgv+c9gjX512Gw6H\njRSnnYwUJzabDUfvXFwDB5E+4QTsmbVHIMWSk5rDsB7DsGFDRLCJDZvYEKIei2AXe+RYpiuT0wtO\nZ0yvMS0evSQidJs2jewLLsCzaRPVq1bj27OHQFUlRWXfUnpoJ/h82H0BxB/A7jONDhvNSO9NSkaf\nZsVw3Ki+fPeU4M++P2AoPVzD9n1VHKzyUO72UVHjo8bnx+c3eP0BvKGvPn8Ab2AEGw1sDCUCh7+G\nHp4SMr37yPLtJ913EKdx4wx4cAbc2E3w5zr4R0vwnxBATDhNmMg5wYAJRP4ICD4/khKCZesnMCv+\njE112MnvnW3BnVtZanfLX0Kbj5RSqguIt6Zg5ZDUL4GhIjJQRFzADGBhnTILgWtCjy8B/tlYQlBK\nKWUty5qPjDE+EbkFWExwSOpzxpg1InI/sMwYsxB4FnhBRIqA/QQTh1JKqXZiaZ+CMWYRsKjOsXuj\nHtcAl1oZg1JKqfjpjGallFIRmhSUUkpFaFJQSikVoUlBKaVUhCYFpZRSEZaukmoFESkD2mp38l5A\ng0tudGH6vsSm70ts+r7E1tbvS39jTG5ThZIuKbQlEVkWzwzArkbfl9j0fYlN35fYOur7os1HSiml\nIjQpKKWUitCk0Lin2zuADkrfl9j0fYlN35fYOuT7on0KSimlIrSmoJRSKkKTQgwi8oiIfCsiq0Tk\nbyLSPercXSJSJCLrReSc9oyzrYnIpSKyRkQCIlJY51xXfl+mhL7vIhGZ3d7xtCcReU5E9oR2VQwf\n6yki74vIxtDXHu0ZY1sTkb4iskRE1oZ+f34aOt4h3xdNCrG9D4w2xowFNgB3AYjIKILLex8DTAH+\nKCKtszFwcvgGuBj4OPpgV35fQt/nHGAqMAqYGXo/uqrnCf4MRJsNfGiMGQp8GHrelfiAnxtjRgEn\nAjeHfkY65PuiSSEGY8x7xhhf6Ol/gILQ4+nAy8YYtzFmC1AETGiPGNuDMWadMWZ9jFNd+X2ZABQZ\nYzYbYzzAywTfjy7JGPMxwb1Rok0H5oUezwMubNOg2pkxpsQYsyL0uBxYB+TTQd8XTQpNuw54J/Q4\nH9gRda44dKyr68rvS1f+3uN1lDGmJPS4FDiqPYNpTyIyABgPfEEHfV8s3WSnIxORD4C8GKfuNsa8\nFSpzN8Gq30ttGVt7iud9USpRxhgjIl1yyKOIZAJvALcZYw6LSORcR3pfumxSMMac1dh5EbkWOB+Y\nFLVv9E6gb1SxgtCxTqOp96UBnf59aURX/t7jtVtE+hhjSkSkD7CnvQNqayLiJJgQXjLG/DV0uEO+\nL9p8FIOITAF+AUwzxlRFnVoIzBCRFBEZCAwFlrZHjB1MV35fvgSGishAEXER7HBf2M4xdTQLgWtC\nj68BulSNU4JVgmeBdcaYx6JOdcj3RSevxSAiRUAKsC906D/GmBtD5+4m2M/gI1gNfCf2XTofEbkI\n+F8gFzgIrDTGnBM615Xfl3OBxwE78Jwx5oF2DqndiMhfgIkEVwDdDfw38CbwKtCP4ArHlxlj6nZG\nd1oicirwb2A1EAgd/iXBfoUO975oUlBKKRWhzUdKKaUiNCkopZSK0KSglFIqQpOCUkqpCE0KSiml\nIjQpKKWUitCkoJRSKkKTglJKqYj/D7YbOfSmhKJBAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "de_2 = pd.Series(np.random.normal(0,2,10000),name = 'μ = 0, σ = 2')\n",
+ "de_3 = pd.Series(np.random.normal(0,3,10000),name = 'μ = 0, σ = 3')\n",
+ "de_0 = pd.Series(np.random.normal(0,0.5,10000), name ='μ = 0, σ = 0.5')\n",
+ "mu_1 = pd.Series(np.random.normal(-2,1,10000),name ='μ = -2, σ = 1')\n",
+ "df = pd.concat([de_2,de_3,de_0,mu_1],axis = 1)\n",
+ "plt.figure(figsize=(20,10))\n",
+ "df.plot.density()\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial7 Random Variables and Distributions.html b/Introduction to Financial Python/Tutorial7 Random Variables and Distributions.html
new file mode 100644
index 0000000..222a9de
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial7 Random Variables and Distributions.html
@@ -0,0 +1,144 @@
+Introduction
+In the last chapter we learned the definition of mean and variance, which are kind of point estimation. Point estimation means using sample data to calculate a single value which is to serve as a 'best estimation' of an unknown population. However, this it not enough because point estimations can be deceiving. We need to use more rigorous methods to test our ideas. That's why we consider distribution and hypothesis testing. Random variable distribution is the basis for almost all quantitative finance topics: linear regression, CAPM, Black-Scholes, binomial tree pricing, etc.
+Random Variables
+First let's start with the concept of random variable. A random variable can be thought of as a drawing from a distribution whose outcome prior to the draw is uncertain. Imaging rolling a dice, you know that your chance of getting each is 1/6, but you don't know what's the number of your next roll is. If we roll the dice N times and record the number of each roll, a collection of those numbers is called discrete random variable. A discrete variable can take on a finite number of values. For our example, we can only take numbers from{1,2,3,4,5,6}.
+The other kind of variable is continuous random variable. A continuous variable can take on any value in a given range. You can think the rate of return as a continuous variable, it theoretically can take any value from \((-\infty, +\infty)\).
+Distributions
+Each random variable follows a probability distribution, which is a function that can be thought of as providing the probabilities of occurrence of different possible outcomes in an experiment. In our dice example, the probability distribution of each number is 1/6. We usually use \(P(X)\) to represents probability distribution function, where X is the outcome value. In our example, \(P(1) = P(2) = p(3) = 1/6\).
+However, we can't use this for a continuous distribution, because the the probability that draw a specific number from a continuous variable is 0, due to the infinity possible outcomes we have. Instead, we use probability density function(PDF) function to describe the probability that a value is in a specific range. We we cover this later.
+For each probability distribution function, we have a cumulative distribution function(CDF). It defines as \(P(X<x)\), which models the probability that the random variable X will take a value less than or equal to x. For discrete random variables, we just sum up the values less than or equal to x and then divide it with number of observations.
+Uniform Distribution
+Uniform distribution is the simplest type of probability distribution. A discrete uniform distribution has equal weight assigned to all outcomes. Both rolling a dice and toss a fare coin are classical uniform distributions.
+Here we use python to simulate rolling a dice 10000 times.
+import random
+import matplotlib.pyplot as plt
+import numpy as np
+import pandas as pd
+def dice():
+ number= [1,2,3,4,5,6]
+ return random.choice(number)
+
+series = np.array([dice() for x in range(10000)])
+print series
+
+We create a series of random variable here. We can plot the values on the x-axis and put their number of occurrences on the y-axis to have a direct view of the distribution:
+plt.figure(figsize = (20,10))
+plt.hist(series,bins = 11,align = 'mid')
+plt.xlabel('Dice Number')
+plt.ylabel('Occurences')
+plt.grid()
+plt.show()
+
+Let's say we want to know the frequency that the observations are less than or equal to 3. In other words we want to seek the value of \(P(X<3)\).
+print len([x for x in series if x <= 3])/float(len(series))
+print np.mean(series)
+
+\(P(X<3)\) is very close to 0.5. This is not surprising because we rolled the dice 1000 times, and the frequency that the observations less than or equal to 3 should be close to the real probability, which is 0.5.
+For a given uniform distribution, it's straightforward to calculate it's mean: it's the center of the distribution because everyone outcome is equal weight. For our dice example, we can think it as
+\[\mu = (1+2+3+4+5+6)/6 = 3.5\]
+Or
+\[E(x) = 1*\frac{1}{6} + 2*\frac{1}{6}+...+6*\frac{1}{6} = 3.5\]
+More generally, if we a assume the minimum value in a uniform distribution is a and the maximum value is b, the mean can be given by:
+\[\bar{u} = \frac{a+b}{2}\]
+Usually we use \(\bar{u}\) to represents the population mean, or the 'real mean'. Here we create a sample with 1000 observations, the mean we calculated above is the sample mean. Sample mean usually doesn't equal to the theoretical population mean unless the number of observation approaches to infinity.
+The variance is given by:
+\[\sigma^2 = \frac{(b-a)^2}{12}\]
+Deducing the formula is out of our lecture scope. It's useful to realize for a given standard distribution, we can formularize its mean and variance.
+Binomial Distribution
+A binomial distribution is a discrete probability distribution of the number of successes in a sequence of n independent experiments. Let's assume that the market has 50% probability goes up and 50% probability goes down, and we observe it in the next 10 days, what's the distribution of the number of days it goes up? This is a binomial distribution example.
+In general, if we carry out the experiment n times, and each outcome is independent, with the same probability of success p, the probability of getting exactly k successes is given by the function:
+\[P(X = K) = C_n^k p^k (1-p)^{n-k}\]
+Where
+\[C_n^k = \frac{n!}{(n-k)!k!}\]
+Under such circumstance we say X follows the binomial distribution \(X \sim B(n,p)\).
+Let's simulate a binomial experiment with success rate p = 0.7 and experiment times n = 10
+def trial():
+ number = [1,2,3,4,5,6,7,8,9,10]
+ a = random.choice(number)
+ if a<= 7:
+ return 1
+ else:
+ return 0
+
+Each time we execute trial(), we did an experiment. If it succeed, it will return 1, otherwise it will return 0. Now we are going to do the experiment 10 times:
+res = [trial() for x in range(10)]
+print sum(res)
+
+Now we did the experiment 10 times, and the number of success is sum(res). However, it just means during these 10 experiments we succeed sum(res) times. If we want to see the binomial distribution, we need experiment N times. When n is large enough, our frequency will approach the theoretical probability. Here we simulate each outcome 10000 times:
+def binomial(number):
+ l = []
+ for i in range(10000):
+ res = [trial() for x in range(10)]
+ l.append(sum(res))
+ return len([x for x in l if x == number])/float(len(l))
+
+print binomial(8)
+
+The number printed above is the simulated probability that we succeed 8 times if we experiment 10 times.
+for each possible outcome, we simulate the probability:
+prob = []
+for i in range(1,11):
+ prob.append(binomial(i))
+prob_s = pd.Series(prob,index = range(1,11))
+print prob_s
+
+Here we got the simulated result of the binomial distribution. Now we are going to check if the simulated frequencies close enough to the theoretical probabilities. Let's take X = 7 and X = 8 as example:
+print (float(factorial(10))/(factorial(7)*factorial(10-7)))*(0.7**7)*(0.3**3)
+print (float(factorial(10))/(factorial(8)*factorial(10-8)))*(0.7**8)*(0.3**2)
+
+As we can see, the simulated results are pretty close to the real probability!
+we can plot the results as follows:
+plt.figure(figsize = (20,10))
+plt.bar(range(1,11),prob)
+plt.grid()
+plt.show()
+
+Another good property of binomial distribution is that its mean and variance are simple enough:
+\[\bar{u} = np\]
+\[\sigma^2 = np(1-P)\]
+We will not introduce the deduction here, but if you are interested in it, we encourage you to do it yourself, based on the probability functions we provided above.
+Normal Distribution
+Before looking at normal distribution, let's first talk about continues distribution. As we mentioned above, we use a probability density function(PDF) to model the probability that our value is taken our a specific range. We define it as:
+\[P(a<X<b) = \int_{a}^{b}f_x(x)dx\]
+Now we can talk about the normal distribution. The normal distribution is most commonly used distribution in natural sciences, of course also in financial research. The PDF of normal distribution is given as follows:
+\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
+Where \(\mu\) is the mean of the normal distribution, and \(\sigma\) is the standard deviation.
+Generally, if a random variable X follows normal distribution, we represent it by \(X\sim N(\mu, \sigma^2)\).
+Specifically, if a normal distribution has a 0 mean and 1 standard deviation, we called it standard normal distribution.
+Now let's simulate a standard normal distribution using Python packages to see what it looks like:
+plt.figure(figsize = (20,10))
+norm.plot.density()
+plt.show()
+
+Financial data is highly disordered and is considered to has lots of noise. Most of the time we believe those noise follows normal distribution. It's also widely believed that the return on an asset over a short period of time follows normal distribution. Let's check it with the daily logarithm rates of return on SPY:
+import quandl
+quandl.ApiConfig.api_key = 'tAyfv1zpWnyhmDsp91yv'
+spy_table = quandl.get('BCIW/_SPXT')
+spy = spy_table.loc['2009':'2017',['Open','Close']]
+spy['log_return'] = np.log(spy.Close).diff()
+spy = spy.dropna()
+
+we calculated the logarithm daily return of S&P 500 index from 2009 to present.
+Let's first have a look at the what the time-series return data looks like:
+plt.figure(figsize = (20,10))
+spy.log_return.plot()
+plt.show()
+
+This is a classic daily return chart. Let's now plot the density chart of the returns:
+plt.figure(figsize = (20,10))
+spy.log_return.plot.density()
+plt.show()
+
+If we observe the x-axis and y-axis carefully, we can see the return of asset is not a standard normal distribution. The peak of the standard normal distribution plot is around 0.4, while it's over 0.6 for this chart. This is because the standard deviation \(\sigma\) of the return is obviously not 1.
+We can demonstrate the normal distribution with different mean and variance by simulation:
+de_2 = pd.Series(np.random.normal(0,2,10000),name = 'μ = 0, σ = 2')
+de_3 = pd.Series(np.random.normal(0,3,10000),name = 'μ = 0, σ = 3')
+de_0 = pd.Series(np.random.normal(0,0.5,10000), name ='μ = 0, σ = 0.5')
+mu_1 = pd.Series(np.random.normal(-2,1,10000),name ='μ = -2, σ = 1')
+df = pd.concat([de_2,de_3,de_0,mu_1],axis = 1)
+plt.figure(figsize=(20,10))
+df.plot.density()
+plt.show()
+
+Summary
+In this chapter we introduced random variable, the difference between discrete random distribution and continuous random distribution, and most importantly, normal distribution. In the next chapter we will introduce how to use these distributions to test our idea or generating trading signals.
diff --git a/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.html b/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.html
new file mode 100644
index 0000000..5debe04
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.html
@@ -0,0 +1,109 @@
+Introduction
+In the last chapter we discussed random variables and random distributions. Now we are going to use the distributions we learned to test our hypothesis and also to model the financial data. When building a trading strategy, it's essential to do some research. However, you won't be able to test your idea using all the data, because it's infinity. You can only use a sample to do your experiment. That's why we need to understand the difference between population and sample, and then use confidence interval to test our hypothesis.
+
+As we mentioned before, both mean and standard deviation are point estimation, and they can be deceiving because sample means are different from population means. Financial data is generated every day now and in the future, thus even though we can use all the data available, it's still just a sample. This is why we need to use confidence interval to attempt to determine how accurate our sample mean estimation is.
+Confidence Interval
+Sample Error
+Let's use the daily return on S&P 500 index from Aug 2010 to present is our population. If we take the recent 10 daily returns to calculate the mean, will it be the same as the population mean? How about increasing the sample size to 1000?
+import matplotlib.pyplot as plt
+import numpy as np
+import pandas as pd
+import quandl
+quandl.ApiConfig.api_key = 'tAyfv1zpWnyhmDsp91yv'
+spy_table = quandl.get('BCIW/_SPXT')
+spy_total = spy_table[['Open','Close']]
+spy_log_return = np.log(spy_total.Close).diff().dropna()
+print 'Population mean:', np.mean(spy_log_return)
+print 'Population standard deviation:',np.std(spy_log_return)
+
+Now let's check the recent 10 days sample and recent 1000 days sample:
+print '10 days sample returns:', np.mean(spy_log_return.tail(10))
+print '10 days sample standard deviation:', np.std(spy_log_return.tail(10))
+print '1000 days sample returns:', np.mean(spy_log_return.tail(1000))
+print '1000 days sample standard deviation:', np.std(spy_log_return.tail(1000))
+
+As we expected, the two samples has different means and variances.
+Confidence Interval
+In order to estimate the range of population mean, we define standard error of the mean as follows:
+\[SE = \frac{\sigma}{\sqrt{n}}\]
+Where \(\sigma \) is the sample standard deviation and \(n\) is the sample size.
+Generally, if we want to estimate an interval of the population so that 95% of the time the interval will contain the population mean, the interval is calculated as:
+\[(\mu - 1.96*SE, \mu + 1.96*SE)\]
+Where \(\mu\) is the sample mean and SE is the standard error.
+This interval is called confidence interval. We usually use 1.96 to calculate a 95% confidence interval because we assume that the sample mean follows normal distribution. We will cover this in detail later.
+Let's try to calculate the confidence interval using the samples above:
+bottom_1 = np.mean(spy_log_return.tail(10))-1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))
+upper_1 = np.mean(spy_log_return.tail(10))+1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))
+bottom_2 = np.mean(spy_log_return.tail(1000))-1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))
+upper_2 = np.mean(spy_log_return.tail(1000))+1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))
+print '10 days 95% confidence inverval:', (bottom_1,upper_1)
+print '1000 days 95% confidence inverval:', (bottom_2,upper_2)
+
+As we can see, the 95% confidence interval became much narrower if we increase the sample size from 10 to 1000. Imagine that if N goes positive infinite, then we have \(\lim_{n\rightarrow \infty}\frac{\sigma}{\sqrt{n}} = 0\). The confidence interval would become a certain value, which is the sample mean!
+Confidence Interval of Normal Distribution
+Normal Distribution is so commonly used that we should be able to remember some critical values of it. Specifically, we usually use 90%, 95% and 99% as the confidence level of a confidence interval. The critical values for these three confidence levels are 1.64, 1.96, and 2.32 respectively. in other words:
+\[\%90 upperabnd = \mu + 1.64*SE\]
+\[\%90 lowerband = \mu + 1.64*SE\]
+The same for other confidence intervals.
+It's also important to remember the famous 'Three sigma rule' or '68-95-99.7' rule associated with normal distribution. This is used to remember the confidence level of the intervals with a width of two, four and six standard deviation. Mathematically:
+\[P(\mu - \sigma \leq X \leq \mu+\sigma)\approx 0.6827\]
+\[P(\mu - 2\sigma \leq X \leq \mu+2\sigma)\approx 0.9545\]
+\[P(\mu - 3\sigma \leq X \leq \mu+3\sigma)\approx 0.9973\]
+This can also be remembered by using the chart:
+ +
+Central Limit Theory
+As we mentioned, if we use the sample to estimate the confidence interval of the population, the 95% confidence interval is:
+\[(\mu - 1.96*SE, \mu + 1.96*SE)\]
+Now you may have some sense to the number 1.96. It's the 95% critical value of a normal distribution. Does this means we assume the mean of sample follows a normal distribution?
+The answer is yes. This assumption is supported by central limit theorem. This theorem tells us that given a sufficiently large sample size from a population with a finite level of variance, the mean of all samples from the same population will be approximately equal to the mean of the population, and the means of the samples will be approximately normal distributed.
+This is the foundation of population mean confidence interval estimation.
+Hypothesis testing
+Now we can talk about hypothesis testing. Hypothesis test is essentially test your inference based on a sample. Let's use our dataset, the daily return of S&P 500 us our population. Assume that we don't know the mean of this population. I guess that the mean of this population is 0. Is my guess correct? I need to test this hypothesis with my sample.
+Let's start from observing our sample:
+mean_1000 = np.mean(spy_log_return.tail(1000))
+std_1000 = np.std(spy_log_return.tail(1000))
+mean_10 = np.mean(spy_log_return.tail(10))
+std_10 = np.std(spy_log_return.tail(10))
+s = pd.Series([mean_10,std_10,mean_1000,std_1000],index = ['mean_10', 'std_10','mean_1000','std_1000'])
+print s
+
+We know how to calculate the confidence interval now. If I were right, i.e. the population mean is 0, then the 90% confidence interval of the sample with 1000 observations should be:
+bottom = 0 - 1.64*std_1000/np.sqrt(1000)
+upper = 0 + 1.64*std_1000/np.sqrt(1000)
+print (bottom, upper)
+
+Our mean of the sample is out of the 90% confidence interval. This means on a 90% confidence level, we can claim that the mean of our population is not 0. In other word, we rejected the hypothesis that the daily return on S&P500 from aug 2010 is zero.
+Can we claim that with 95% confidence level?
+bottom = 0 - 1.96*std_1000/np.sqrt(1000)
+upper = 0 + 1.96*std_1000/np.sqrt(1000)
+print (bottom, upper)
+
+This time the sample mean is within the confidence interval. Thus we can't reject my hypothesis. In other words, we can't claim with 95% confidence level that the mean return is positive. Even though we can claim it with 90% confidence level.
+We have actually already finished a hypothesis testing above! In general, we have null hypothesis \(H_0\) and alternative hypothesis. They are usually in the following forms:
+\[H_0:\bar{\mu} = 0\]
+\[H_0:\bar{\mu} \neq 0\]
+If the tested value is outside the confidence interval, we reject the null hypothesis, or accept the alternative hypothesis; If the tested value is within the confidence interval, we can't reject the null hypothesis.
+Although the hypothesis testing method we used above is straightforward, it's not so convenient to implement. Instead, we reverse the process to calculate the critical value, or Z-score. Z-score is defined as:
+\[Z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\]
+Let's calculate the Z score from our sample:
+print np.sqrt(1000)*(mean_1000 - 0)/std_1000
+
+We know that the critical value for the 90% confidence level is 1.64 and that for the 95% confidence level is 95%. The higher the Z score is, the further the tested value is from the hypothesized value(which is 0 in this example). Thus with 90% confidence level, we are far away enough from zero and we reject the null hypothesis. However with 95% confidence level, we are not far away enough from zero, so we can't reject the null hypothesis.
+one reason of doing in this way is that we can know how wide our confidence interval is. In our example, the z-score is 1.8488. We can know the width is the confidence interval referring to a normal distribution table. Of course we can do this in Python:
+import scipy.stats as st
+print (1 - st.norm.cdf(1.9488))
+
+It's worth noting that st.norm.cdf will return the probability that a value take from the distribution is less than our tested value. In other words, 1 - st.norm.cdf(1.9488) will return the probability that the value is greater than our tested value, which is 0.025659 in this example. This calculated number is called p-value. If our confidence level our confidence interval is 95%, then we have 2.5% on the left side and 2.5% on the right side. This is called two-tail test. If our null hypothesis is \(\mu = 0\), we are conducting two-tail test because the tested sample mean can be either positive enough or negative enough to reject the null hypothesis. We can see it from the chart:
+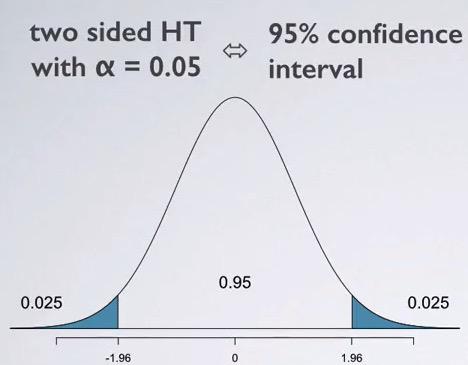 +If we use 95% confidence interval, we need a p-value less than 0.025 to reject the null hypothesis. However, now our p-value is 0.025659, which is greater than 0.025, thus we can't reject the null hypothesis. It's obviously less than 0.05, so we can still reject the null hypothesis with 90% confidence level.
+Now let's test the hypothesis that population mean = 0 again with a large sample, which has 1200 observations:
+
+If we use 95% confidence interval, we need a p-value less than 0.025 to reject the null hypothesis. However, now our p-value is 0.025659, which is greater than 0.025, thus we can't reject the null hypothesis. It's obviously less than 0.05, so we can still reject the null hypothesis with 90% confidence level.
+Now let's test the hypothesis that population mean = 0 again with a large sample, which has 1200 observations:
+mean_1200 = np.mean(spy_log_return.tail(1200))
+std_1200 = np.std(spy_log_return.tail(1200))
+z_score = np.sqrt(1200)*(mean_1200 - 0)/std_1200
+print 'z-score = ',z_score
+p_value = (1 - st.norm.cdf(z_score))
+print 'p_value = ',p_value
+
+Using the a larger sample, now we can reject the null hypothesis with a higher confidence interval! our p-value is 0.0105, and it's a two-tail test, so our confidence level of the interval is 1-(0.0105*2) = 0.979. We can say at most with 97.9% confidence interval, we can claim that the population mean is not zero. We already know that the population mean is not 0. As our sample size increasing, the accurate rate of our hypothesis goes up.
+Summary
+In this chapter we introduced confidence interval, especially that for the normal distribution, and hypothesis test. Now we know how to test our idea rigorously. Normal distribution and it's confidence interval can be applied to many quantitative finance theories, we will see it frequently in our following tutorials.
diff --git a/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.ipynb b/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.ipynb
new file mode 100644
index 0000000..841ef73
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial8 Confidence Interval and Hypothesis Testing.ipynb
@@ -0,0 +1,229 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Population mean: 0.000552553099108\n",
+ "Population standard deviation: 0.00914773017108\n"
+ ]
+ }
+ ],
+ "source": [
+ "import matplotlib.pyplot as plt\n",
+ "import numpy as np\n",
+ "import pandas as pd\n",
+ "import quandl\n",
+ "quandl.ApiConfig.api_key = 'tAyfv1zpWnyhmDsp91yv'\n",
+ "spy_table = quandl.get('BCIW/_SPXT')\n",
+ "spy_total = spy_table[['Open','Close']]\n",
+ "spy_log_return = np.log(spy_total.Close).diff().dropna()\n",
+ "print 'Population mean:', np.mean(spy_log_return)\n",
+ "print 'Population standard deviation:',np.std(spy_log_return)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "10 days sample returns: 0.0011564735434\n",
+ "10 days sample standard deviation: 0.00221735894302\n",
+ "1000 days sample returns: 0.000464511512788\n",
+ "1000 days sample standard deviation: 0.00780054327516\n"
+ ]
+ }
+ ],
+ "source": [
+ "print '10 days sample returns:', np.mean(spy_log_return.tail(10))\n",
+ "print '10 days sample standard deviation:', np.std(spy_log_return.tail(10))\n",
+ "print '1000 days sample returns:', np.mean(spy_log_return.tail(1000))\n",
+ "print '1000 days sample standard deviation:', np.std(spy_log_return.tail(1000))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "10 days 95% confidence inverval: (-0.00021785976801675451, 0.0025308068548152993)\n",
+ "1000 days 95% confidence inverval: (-1.8971168442191949e-05, 0.00094799419401722998)\n"
+ ]
+ }
+ ],
+ "source": [
+ "bottom_1 = np.mean(spy_log_return.tail(10))-1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))\n",
+ "upper_1 = np.mean(spy_log_return.tail(10))+1.96*np.std(spy_log_return.tail(10))/(np.sqrt(len((spy_log_return.tail(10)))))\n",
+ "bottom_2 = np.mean(spy_log_return.tail(1000))-1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))\n",
+ "upper_2 = np.mean(spy_log_return.tail(1000))+1.96*np.std(spy_log_return.tail(1000))/(np.sqrt(len((spy_log_return.tail(1000)))))\n",
+ "print '10 days 95% confidence inverval:', (bottom_1,upper_1)\n",
+ "print '1000 days 95% confidence inverval:', (bottom_2,upper_2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "mean_10 0.001156\n",
+ "std_10 0.002217\n",
+ "mean_1000 0.000465\n",
+ "std_1000 0.007801\n",
+ "dtype: float64\n"
+ ]
+ }
+ ],
+ "source": [
+ "mean_10 = np.mean(spy_log_return.tail(10))\n",
+ "std_10 = np.std(spy_log_return.tail(10))\n",
+ "mean_1000 = np.mean(spy_log_return.tail(1000))\n",
+ "std_1000 = np.std(spy_log_return.tail(1000))\n",
+ "s = pd.Series([mean_10,std_10,mean_1000,std_1000],index = ['mean_10', 'std_10','mean_1000','std_1000'])\n",
+ "print s"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "(-0.0004045467332738398, 0.0004045467332738398)\n"
+ ]
+ }
+ ],
+ "source": [
+ "bottom = 0 - 1.64*std_1000/np.sqrt(1000)\n",
+ "upper = 0 + 1.64*std_1000/np.sqrt(1000)\n",
+ "print (bottom, upper)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "(-0.00048348268122971096, 0.00048348268122971096)\n"
+ ]
+ }
+ ],
+ "source": [
+ "bottom = 0 - 1.96*std_1000/np.sqrt(1000)\n",
+ "upper = 0 + 1.96*std_1000/np.sqrt(1000)\n",
+ "print (bottom, upper)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "1.88309240519\n"
+ ]
+ }
+ ],
+ "source": [
+ "print np.sqrt(1000)*(mean_1000 - 0)/std_1000"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "0.025659656888\n"
+ ]
+ }
+ ],
+ "source": [
+ "import scipy.stats as st\n",
+ "print (1 - st.norm.cdf(1.9488))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "z-score = 2.33417302452\n",
+ "p_value = 0.009793331898\n"
+ ]
+ }
+ ],
+ "source": [
+ "mean_1200 = np.mean(spy_log_return.tail(1200))\n",
+ "std_1200 = np.std(spy_log_return.tail(1200))\n",
+ "z_score = np.sqrt(1200)*(mean_1200 - 0)/std_1200\n",
+ "print 'z-score = ',z_score\n",
+ "p_value = (1 - st.norm.cdf(z_score))\n",
+ "print 'p_value = ',p_value"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 2",
+ "language": "python",
+ "name": "python2"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Introduction to Financial Python/Tutorial9 Simple Linear Regression.html b/Introduction to Financial Python/Tutorial9 Simple Linear Regression.html
new file mode 100644
index 0000000..0ee7f8b
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial9 Simple Linear Regression.html
@@ -0,0 +1,78 @@
+Introduction
+In finance and economics filed, most of the models are linear ones. We can see linear regression everywhere, from the foundation of the model portfolio theory to the nowadays popular Fama-French asset pricing model. It's very important to understand how linear regression works in order to have a comprehensive understanding of those theories.
+
+If we are holding a stock, we must be curious about the relationship between our stock return and the market return. Let's say we hold Amazon stock on the first day of this year. In order to see the relation directly, we plot the daily return of our stock on the y-axis and plot the S&P 500 index daily return on the x-axis.
+import numpy as np
+import pandas as pd
+import quandl
+quandl.ApiConfig.api_key = '_fgkxjSbt5389zGt4crC'
+spy_table = quandl.get('BCIW/_SPXT')
+amzn_table = quandl.get('WIKI/AMZN')
+spy = spy_table.loc['2017':'2017-6',['Close']]
+amzn = amzn_table.loc['2017':'2017-6',['Close']]
+spy_log = np.log(spy.Close).diff().dropna()
+amzn_log = np.log(amzn.Close).diff().dropna()
+df = pd.concat([spy_log,amzn_log],axis = 1).dropna()
+df.columns = ['spx','amzn']
+print df.tail()
+
+We successfully create a DataFrame contains the daily logarithm return of Amazon stock and S&P500. Now let's plot it:
+import matplotlib.pyplot as plt
+plt.figure(figsize = (15,10))
+plt.scatter(df.spy,df.amzn)
+plt.show()
+
+The plot is scattered, but we can see they are approximately correlated: generally the higher SPX's daily return is, the higher Amazon stock's return is. This is called positively correlated. We will cover it in the following tutorials.
+Slope and Intercept
+It's natural that we want to model the relation between these two rates of return. Intuitively we use a straight line to model it, this is called Linear Regression. In order to find the best straight line, it's natural to think that the vertical distances between the points of the data set and the fitted line should be minimized. Those vertical distances are called residual. Our objective is to make the sum of squared residuals as small as possible. This method is called ordinary least square, or OLS method.
+We use x and y to represent the two variable, S&P 500 daily returns and AMZN daily returns. The linear relation is:
+\[Y = Y = \alpha + \beta*X + \epsilon\]
+Where \(\alpha\) is called intercept, \(\beta\) is called slope.
+Generally, if the scatter points can be represented by\(\left\{\right (x_1,y_1),(x_2, y_2),(x_3,y_3)...(x_n,y_n) \left\}\right\), then the intercept and slope are given by:
+\[\beta = \frac{\sum_{i=1}^{n}(x-\bar{x})(y-\bar{y})}{\sum_{i=1}^{n}(x-\bar{x})^2}\]
+\[\alpha = \bar{y} - \hat{\beta}\bar{x}\]
+Where \(\bar{x}\) is the mean of X, \(\bar{y}\) is the mean of Y.
+In python, we don't need to do the above calculation manually because we have package for it. But it still very important to understand the calculation process of \(\beta\) in order the understand the modern portfolio theory and CAPM, which we will cover in the future.
+Python Implementation
+In python, we have a very power package for mathematical models, which is named 'statsmodels'.
+import statsmodels.formula.api as sm
+model = sm.ols(formula = 'amzn~spy',data = df).fit()
+print model.summary()
+
+We built a simple linear regression model above by using the ols() function in statsmodels. The 'model' instance has lots of properties. The most commonly used one is parameters, or slope and intercept. We can access to them by:
+print 'pamameters: ',model.params
+print 'residual: ', model.resid.tail()
+print 'fitted values: ',model.predict()
+
+Now let's have a look at our fitted line:
+plt.figure(figsize = (15,10))
+plt.scatter(df.spy,df.amzn)
+plt.xlabel('spx_return')
+plt.ylabel('amzn_return')
+plt.plot(df.spy,model.predict(),color = 'red')
+plt.show()
+
+The red line is the fitted linear regression straight line.
+As we can see there are lot of statistical results in the summary table. Now let's talk about some important statistical parameters.
+Parameter Significance
+From the summary table we can see 'std err'. This means standard errors of the intercept and slope. The null hypothesis here is \(H_0: \beta = 0\), and the alternative hypothesis is \(H_1: \beta \neq 0\). This hypothesis score is calculated by:
+\[t = \frac{\beta - 0}{SE}\]
+Where SE is given by:
+\[SE = \sqrt\frac{\frac{1}{n-2}\sum_{i = 1}^{n}\hat{\epsilon}^2}{\sum_{i = i}^{n}(x_i - \bar{x})^2}\]
+The distribution used here is 'Student's t-distribution'. It's different from normal distribution but used in the similar way. The column 't' in this table is the test score, and 'p>|t|' is the p-value. By observing the p-value, we can see that the significance level of spy, or the slope, is very high because the p-value is close to zero. In other words, we have 99.999 confidence to claim that the slope is not 0, and there exists linear relation between X and Y. However, regarding the intercept, the p-value is 0.923, which means we have only 7.7% confidence level that the value of intercept is not 0. We can also see from the plot that the line crosses the origin.
+The following 2 columns are the lower band and upper band of the parameters at 95% confidence interval. At 95% confidence level, we can claim that the true value of the parameter is within this range.
+Model Significance
+R-square
+Sum of Squared Errors, or SSE, is used to measure the difference between the fitted value and the actual value. It's given by:
+\[SSE = \sum_{i=1}^{n}(y_i - \hat{y_i})^2 = \sum_{i = 1}^{n}\hat{\epsilon_i}^2\]
+If the linear model perfectly fitted the sample, the SSE would be zero.
+The reason we use squared error here is that the positive and negative errors would offset each other if we simply summed them up.
+Another measurement of the dispersion of the sample is called total sum of squares, or SS.. it's given by:
+\[SS = \sum_{i = i}^{n}(y_i - \bar{y}_i)^2\]
+If you are familiar with variance, we can see that SS divided by the number of sample n is the sample variance.
+From SSE and SS, we can calculate the Coefficient of Determination, or r-square for short. R-square means the proportion of variation that 'explained' by the linear relationship between X and Y, it's calculated by:
+\[r^2 =1 = \frac{SSE}{SS} =1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2}{\sum_{i = i}^{n}(y_i - \bar{y}_i)^2}\]
+Let's assume that the model perfectly fitted the sample, which means all of the sample points lie on the straight line. Then the SSE would become zero, and the r-square would become 1. This means perfect fitness. The higher r-square is, the more parts of variation can be explained by the linear relation, the higher significance level the model is.
+Some other parameters, such as F-statistic, AIC and BIC, are related to multiple linear regression, with would be cover in the next chapter.
+Summary
+In this chapter we introduced how to implement simple linear in python, and focused on how to read the summary table. In next chapter we will introduced multiple linear regression, which are commonly used to built models in finance and economics.
diff --git a/Introduction to Financial Python/Tutorial9 Simple Linear Regression.ipynb b/Introduction to Financial Python/Tutorial9 Simple Linear Regression.ipynb
new file mode 100644
index 0000000..6055db3
--- /dev/null
+++ b/Introduction to Financial Python/Tutorial9 Simple Linear Regression.ipynb
@@ -0,0 +1,259 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "import numpy as np\n",
+ "import pandas as pd\n",
+ "import quandl\n",
+ "quandl.ApiConfig.api_key = '_fgkxjSbt5389zGt4crC'\n",
+ "spy_table = quandl.get('BCIW/_SPXT')\n",
+ "amzn_table = quandl.get('WIKI/AMZN')\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {
+ "collapsed": true
+ },
+ "outputs": [],
+ "source": [
+ "spy = spy_table.loc['2016',['Close']]\n",
+ "amzn = amzn_table.loc['2016',['Close']]\n",
+ "spy_log = np.log(spy.Close).diff().dropna()\n",
+ "amzn_log = np.log(amzn.Close).diff().dropna()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | \n",
+ " spy | \n",
+ " amzn | \n",
+ "
\n",
+ " \n",
+ " | Date | \n",
+ " | \n",
+ " | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 2016-12-23 | \n",
+ " 0.001351 | \n",
+ " -0.007531 | \n",
+ "
\n",
+ " \n",
+ " | 2016-12-27 | \n",
+ " 0.002254 | \n",
+ " 0.014113 | \n",
+ "
\n",
+ " \n",
+ " | 2016-12-28 | \n",
+ " -0.008218 | \n",
+ " 0.000946 | \n",
+ "
\n",
+ " \n",
+ " | 2016-12-29 | \n",
+ " -0.000247 | \n",
+ " -0.009081 | \n",
+ "
\n",
+ " \n",
+ " | 2016-12-30 | \n",
+ " -0.004601 | \n",
+ " -0.020172 | \n",
+ "
\n",
+ " \n",
+ "
\n",
+ "
 +We simulated this graph using 10 stocks. In the real world there are far more than 10 assets, but the graph would be almost the same shape. Before demonstrating how to simulate this, we should totally understand it.
+
+The black curve is called efficient frontier. More accurately speaking, only the part above the blue dash-line is. Efficient frontier means that for a given expected return, you can't achieve a standard deviation lower than that of the portfolio on the efficient frontier. In other words, all of the assets and possible portfolio should lie inside the efficient frontier.
+
+Start from the definition of efficient frontier, we know that for any given standard deviation, the portfolio on the efficient frontier has a higher return, so we would only choose the portfolio on the efficient frontier. However, we have infinite number of portfolios on the efficient frontier, which one should we choose? Now we need to understand the concept of Sharpe Ratio.
+
+We simulated this graph using 10 stocks. In the real world there are far more than 10 assets, but the graph would be almost the same shape. Before demonstrating how to simulate this, we should totally understand it.
+
+The black curve is called efficient frontier. More accurately speaking, only the part above the blue dash-line is. Efficient frontier means that for a given expected return, you can't achieve a standard deviation lower than that of the portfolio on the efficient frontier. In other words, all of the assets and possible portfolio should lie inside the efficient frontier.
+
+Start from the definition of efficient frontier, we know that for any given standard deviation, the portfolio on the efficient frontier has a higher return, so we would only choose the portfolio on the efficient frontier. However, we have infinite number of portfolios on the efficient frontier, which one should we choose? Now we need to understand the concept of Sharpe Ratio.
+ +The blue curve in the chart above is the efficient frontier formed by the portfolios with only three stocks: IBM, GE, and PFE. Obviously the portfolios on this curve has lower sharpe ratio than the portfolios on the original efficient frontier. As the number of stocks increases, the efficient frontier becomes better.
+
+The blue curve in the chart above is the efficient frontier formed by the portfolios with only three stocks: IBM, GE, and PFE. Obviously the portfolios on this curve has lower sharpe ratio than the portfolios on the original efficient frontier. As the number of stocks increases, the efficient frontier becomes better.
+ +If we use 95% confidence interval, we need a p-value less than 0.025 to reject the null hypothesis. However, now our p-value is 0.025659, which is greater than 0.025, thus we can't reject the null hypothesis. It's obviously less than 0.05, so we can still reject the null hypothesis with 90% confidence level.
+Now let's test the hypothesis that population mean = 0 again with a large sample, which has 1200 observations:
+
+If we use 95% confidence interval, we need a p-value less than 0.025 to reject the null hypothesis. However, now our p-value is 0.025659, which is greater than 0.025, thus we can't reject the null hypothesis. It's obviously less than 0.05, so we can still reject the null hypothesis with 90% confidence level.
+Now let's test the hypothesis that population mean = 0 again with a large sample, which has 1200 observations:
+