Skip to content

Latest commit

 

History

History
630 lines (424 loc) · 16.1 KB

menu2.md

File metadata and controls

630 lines (424 loc) · 16.1 KB
Raw

@def title = "Solutions" @def hascode = true @def rss = "here" @def rss_title = "Solutions" @def rss_pubdate = Date(2019, 5, 1)

@def tags = ["syntax", "code", "image"]

\toc

Lab Two

Some of the solutions here are difficult to understand. If you want to understand them, you should come to tutorial! This list is not a substitute for tutorial (or office hours).

Problem 9

Q: If Alist=[9,-4,33,2,89,100,36,11], what is Alist[2]? What is Alist[2][1]?

A: Test it out and see for yourself! Email any questions and I'll be happy to answer.

Problem 10

Q: In the cases provided in the problem set, predict the behavior of the code, and check for yourself.

A: Covered in-depth during lecture; solution not provided.

Problem 11

Write a code to find $$\sum_{j=1}^{10,000} \frac{1}{j}$$

val = 0
for j in range(1,10_001):
    val += 1/j

val

or

sum(1/i for i in range(1,10_001))

Problem 12

Write code to find $$\sum_{m=1}^{600} \sum_{n=10}^{450} \frac{m}{n}$$

val = 0 
for m in range(1, 601):
    for n in range(10, 451):
        val += m/n

val

Problem 13

Find the sum of all positive integers from 1 to 1000 which are not divisible by 4 or 5

sum([i for i in range(1,1000) if i % 4 != 0 and i % 5 != 0])

Problem 14

Create a list of squares of all numbers $x$, where $1 \leq x \leq 20,000$, and $x$ is divisible by $7$.

sList = []

for i in range(1,20_001):
    if i % 7 == 0:
        sList.append(i**2)

sList

or

[x**2 for x in range(1,20_001) if x % 7 == 0]

Problem 15

From a list of squares of numbers $x$, where $1 \leq x \leq 100,000$, remove all entries which start with $9$ and end with $0$ or $1$.

sList = []

for x in range(1,100_001):
    if(str(x**2)[0] == "9"):
        if(str(x**2)[-1] == "0" or str(x**2)[-1] == "1"):
            pass
        else:
            sList.append(x**2)
    else:
        sList.append(x**2)

sList

or

[x**2 for x in range(1,101) if ((str(x**2)[0] != "9") and (str(x**2)[-1] != "0") or (str(x**2)[-1] != "1"))]

Problem 16

Write a code to determine whether a given year is a leap year or not. Input: a year between $1600$ and $2200$. Output: Year $1997$ is not a leap year. Year $2004$ is a leap year. etc.

note: years divisible by 4 are leap years, except if they are divisible by 100 but not divisible by 400. Thus, 1700, 1800, 1900, 2100 are not leap years, but 2000, 2400 are leap years.

def IsLeapYear(year: int) -> bool:
    return(year in [year for year in range(1600, 2500) if ((year % 4 == 0) and not (year % 100 == 0 and year % 400 != 0))])

Problem 17

Find the sum of all digits used in writing down the numbers from 1 to 2 million (including 1 and including 2 million).

sum([sum(map(int,str(x))) for x in range(1,2_000_001)])

Problem 18

Write a Python code which computes the sum

$$S=\sum_{i^{}=1}^{10000} \frac{1}{i^{}}$$

where $i^*$ is a number written without the number seven, e.g.

$$S=\frac{1}{1}+\cdots+\frac{1}{6}+\frac{1}{8}+\cdots+\frac{1}{16}+\frac{1}{18}+\cdots+\frac{1}{69}+\frac{1}{80}+\cdots+\frac{1}{10000}$$

sum([int for int in range(1,10001) if "7" not in str(int)])

Problem 19

You are speeding on a highway and a police officer stops you. Write a code to compute the fine that you might have to pay (call the variable fine), based on the following rules (assume that the speed is a positive integer):

  • If your speed is 110 km/h or less, the fine is zero.
  • If your speed is between 111 and 130 inclusive, the fine is 150.
  • If your speed is above 130 km/h, the fine is 350.
  • If it is your birthday, your speed can be 5 km/h higher in all cases (use your actual birthday, or make one up)
  • For instance, if you drive 114 km/h on your birthday, your fine is zero. If you drive 118 km/h on your birthday, your fine $150. If you drive 114 km/h and it’s not your birthday, your fine is $150.
def FineValue(speed: int, isBirthday: bool) -> int:

    fine = 0

    if(isBirthday == 1):
        speed -= 5

    if(111 <= speed <= 130):
        fine = 150

    if( 130< speed):
        fine = 350

    return fine

Problem 20

Let $M = 123456 ... 99979998999910000$ (i.e., M is obtained by writing all numbers from $1$ to $10000$ next to each other)

  • How many digits does $M$ have?
  • How many times does the number $7$ appear in $M$?
digits = 0
sevens = 0
for i in range(1, 10_001):
    for j in str(i):
        digits += 1
        if j == "7":
            sevens += 1

print(digits)
print(sevens)

Problem 21

Problem Twenty One

Let $N = 124567891011121415 ...282940414244 ...999799989999$ (i.e., N is obtained by writing all numbers from 1 to 9999 that do not contain digit 3)

  • How many digits does N have?
  • Is $N$ divisible by three?
N = ""
for i in range(1,10_000):
    N += str(i)

len(N)
int(N) % 3

Problem 22

Create a list with the following pattern:

write natural numbers in a sequence and remove all numbers which are either divisible by 3 or contain the digit 3. Find the 10,000th number in this list

and find the 10'000th element in this list

aList = []
val = 0

while (len(aList) <= 10_001):
    val += 1
    if(val % 3 != 0  and "3" not in str(val)):
        aList.append(val)

aList[10_001]

Problem 23

Problem Twenty Three

Write a code that computes the transpose of some matrix M, of the form:

M=[[1,2,3],[4,5,6],[7,8,9]]

from typing import List

def Transpose(M:List[List]) -> List[List]:
    """This transposes a matrix :D"""
    return([[row[i] for row in M] for i in range(len(M[0]))])

Problem 24

Given a non-empty list of numbers (call in num), write a code to find the largest and the smallest numbers in num. Then compare with the built-in functions max(num) and min(num).

from typing import List, Union
import math

def BruteMin(num: List[Union[int, float]]) -> Union[int, float]:
    """Returns the smallest number from a list of numbers"""
    min = math.inf
    for i in num:
        if(i < min):
            min = i
    
    return min 


def BruteMax(num: List[Union[int, float]]) -> Union[int, float]:
    """Returns the largest number from a list of numbers"""
    max = -math.inf
    for i in num:
        if(i > max):
            max = i
    
    return max

Problem 25

Define the function is prime(p) which returns True if $p$ is a prime number and False otherwise. You can assume that $p$ is an integer, $p \geq 1$.

def IsPrime(p:float) -> bool:
    """Checks if a number is prime!"""
    if p == 1: return False
    return all([p % i for i in range(2,p)])

Problem 26

Define the function all divisors(n), where $n &gt; 0$, which stores all divisors of $n$ (including $1$ and $n$) into a list.

from typing import List

def nDivisors(n:int) -> List[int]:
    """Returns all divisors of integer n"""
    return [j for j in range(1, n+1) if n % j == 0]

Problem 27

Print “I love math” once, then “I hate math” once; then “I love math” two times, then “I hate math” once; then “I love math” three times, then “I hate math” once; then “I love math” four times, then “I hate math” once, and so on, until a total of 100 lines are printed.

val = 0
for i in range(1,101):
    if i % 2 != 0:
        val += 1
        print(val*"I love math ")
    else:
        print("I hate math")

Problem 28

Create a list A so that A[i] = sum of digits of i, for $0 \leq i \leq 10000$, i.e.,

A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4,..., 1]

A = [sum(map(int, str(i))) for i in range(1,10_000)]

Problem 29

Create a list of the first 100 prime numbers.

primes = []
counter = 1
while len(primes) < 100:
    # Using problem 25 function `IsPrime`
    if(IsPrime(counter) == 1):
        primes.append(counter)
    counter += 1

Post Test-One

\newcommand{\note}[2]{ @@definition Note: !#1

#2 @@ }

At the request of some students, here are some later problems. The numbering scheme changes across the versions of the problem sets, so in this case, I am using the 28 February - 4 March problem set.

Some solutions contain graphs, or programming concepts that you may not have covered in lecture (e.g. comprehensions) --- though I'm trying to avoid the later one for these solutions --- so don't worry about this if you haven't seen it before. The graphs especially are simply a nice way to view the solution. Don't worry about it.

Problem 58, 68

Write a function Newton(f,fprime,x0,tol,max steps) which produces a list of approximations (starting with x0) of a solution to f(x) = 0 using Newton’s method. Stop the process when either the number of steps reaches max steps or the value of f is less than tol. Recall that Newton’s method gives a sequence of approximations:

$$x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)}$$

which, for a differentiable function, approximate a solution $f(x) = 0$ (if $x_0$ is close to it).

Test your function on $[-1,3]$ by solving:

$$f(x)=x^{3}-x^{2}-2 x+3 \sin (2 x)=0$$

Soln: first, we write the functions for $f$, $f^\prime$.

def f(x: complex) -> complex:
    return x**3 - x**2 - 2*x + 3*np.sin(2*x)

def fPrime(x: complex) -> complex:
    return 3*x**2 -2*x +6*np.cos(2*x - 2)

The question asks for these both, and so the assumption is that it wants an analytic solution to the derivative. We will also extend the question, and explore the case where the derivative is not computed analytically, and so not required as a function argument. The solution for Newton's method follows:

import numpy as np
import math

def Newton(function, derivative, x0:float, tol:float, max_steps:int) -> float:
    """A simple Newton's method solution to a function with a known derivative."""
    ratio = math.inf
    x = x0
    steps = 0

    while(abs(f(x)) > tol):
        ratio  = function(x)/derivative(x)
        x = x - ratio

        if steps > max_steps:
            break

    return(x)

We would like to extend this into the case where the derivative $f(x)$ is not know a priori (it isn't in most real life scenarios). To do this, we write a function to compute the derivative $f(x)$ of some given input $F(x)$. This is a separate problem in the worksheet (68), but we solve it here instead. To find the derivative, we go back to calculus one, and use the difference quotient:

$$f(x) = \frac{F(x + h) - F(x)}{h}$$

def Diff(f, x, h = 0.001) -> float:
    """This gives us a crude approximation to the first derivative of f"""
    return (f(x + h) - f(x))/h

We can rewrite Newton's method using this as:

def Newton(function, x0:float, tol:float, max_steps:int) -> float:
    """A simple Newton's method solution to a function with an unknown derivative."""
    ratio = math.inf
    x = x0
    steps = 0

    while(abs(f(x)) > tol):
        ratio  = function(x)/Diff(f,x)
        x = x - ratio

        if steps > max_steps:
            break

    return(x)

Now, this is a decent approximation, but it fails in some major respects (if you want to know more, take a numerical analysis course!). We can construct a much more clever approximation to the derivative using a simple Taylor series trick. (you can ignore this if you want; it won't show up on your test. it is very cool though.)

Given some function $f: \mathbb{R} \to \mathbb{R}$, we can construct the taylor series with:

$$f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n !}(x-a)^{n}=f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime \prime}(a)}{2 !}(x-a)^{2}+\ldots (\text{error})$$

$$f(x)=f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime \prime}(a)}{2 !}(x-a)^{2}+\ldots (\text{error})$$

Now instead of taking a step along the real axis for $h$ small, we instead step along the complex axis, taking $ih$ small. That is, we evaluate:

$$f(x + ih)$$

Which gives us Taylor series:

$$f(x+\mathrm{i} h)=f(x)+\mathrm{i} h f^{\prime}(x)-h^{2} \frac{f^{\prime \prime}(x)}{2}+ \text{error}$$

Where the error shrinks as we bring $h$ small. We can take the imaginary part of both sides to yield:

$$Im(f(x+\mathrm{i} h))=Im \left(f(x)+\mathrm{i} h f^{\prime}(x)-h^{2} \frac{f^{\prime \prime}(x)}{2}+ \text{error} \right)$$ $$Im(f(x+\mathrm{i} h))= h f^{\prime}(x) + \text{error} $$

And then rearrange to solve for the derivative:

$$\frac{Im(f(x+\mathrm{i} h))}{h} + \text{error}=f^{\prime}(x) $$

$$f^{\prime}(x) = \frac{Im(f(x+\mathrm{i} h))}{h} + \text{error} $$

It's like magic! We can use this to define a nicer formula for the derivative for use in our question:

def Cstep(f, x, h = 0.001) -> float:
    return np.imag(f(x+ 1j*h))/h

This numerical computation of the derivative is much more well behaved, for numerical analysis reasons (subtracting two floating point numbers of similar sizes can destroy your accuracy, and it also converges faster). We plug this into our initial Newton's method function to get:

def Newton(function, x0:float, tol:float, max_steps:int) -> float:
    """A simple Newton's method solution to a function with an unknown derivative."""
    ratio = math.inf
    x = x0
    steps = 0

    while(abs(f(x)) > tol):
        ratio  = function(x)/Cstep(f,x)
        x = x - ratio

        if steps > max_steps:
            break

    return(x)

As a quick side note, the reason I don't type hint functions as inputs (here) is that I don't think type hinting objects as callable is helpful for the only purpose I'm using type hints in these solutions --- easier to read functions.

Problem 59

Assume that $x \in \mathbb{R}$ represents an angle in radians. Reduce this angle to an angle in $[0,2 \pi)$.

import math

def angle_reduce(x: float) -> float:
    return x % (2*math.pi)

Question: the following code doesn't return the correct answer:

import math

def angle_reduce(x: float) -> float:
    return x % 2*math.pi

Why?

\note{Order of Operations}{ The function without the brackets evaluates left to right, calculating (x % 2)*math.pi, which isn't what you want. }

Problem 60

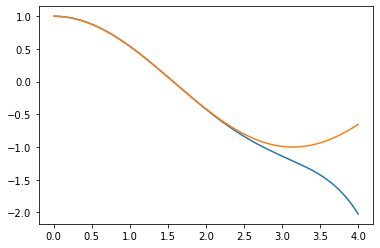
Write a code for the function cos_series(x) which calculates an approximate value of $cos(x)$, where $x \in \mathbb{R}$, based on the partial sum (of the Maclaurin series) which consists of the first 25 terms. If $x$ is not in $[0, 2π)$, reduce it to that interval.

$$cos(x) = \sum_0^{1000} \frac{-1^n}{2n!} x^{2n}$$

Note that I am not going to reduce the angle in my solution, because I think it leads to a nicer graph, and I just solved that in the previous question.

import numpy as np
import matplotlib.pyplot as plt

def cos_series(x:float) ->float:
    out = 0
    for n in range(0,4):
        out += (((-1)**n)/(np.math.factorial(2*n)))*x**(2*n)
    return out

x = np.linspace(0,4,2000)
yVals = [cos_series(xi) for xi in x]
yTrue = [np.math.cos(xi) for xi in x]
plt.plot(x, yVals)
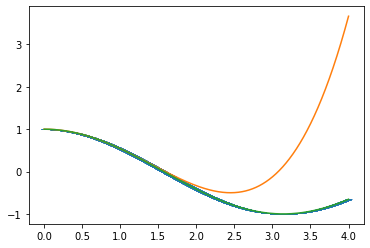
plt.plot(x, yTrue)

taylor's version

Problem 61

Write a code for the function cos_series(x,tol=1e-7,max terms=15) that calculates an approximate value of $cos(x)$, where $x \in [0, 2\pi)$. You will use a partial sum of the Maclaurin series for $cos(x)$, and end it, depending on which of the following two events happens first: 15 terms are added, or the next term to be added is less than the tolerance tol.

$$cos(x) = \sum_0^{1000} \frac{-1^n}{2n!} x^{2n}$$

import numpy as np
import matplotlib.pyplot as plt

def cos_series_2(x: float, tol = 1e-7, max_steps = 15):
    """Cos taylor series approximation"""
    out = 0
    n = 0
    while(abs(out-np.math.cos(x)) > tol):
        out += (((-1)**n)/(np.math.factorial(2*n)))*x**(2*n)
        n += 1
        if n >= max_steps:
            return out
    return out

x = np.linspace(0,4,2000)
yVals = [cos_series_2(xi) for xi in x]
yVals3 = [cos_series_2(xi, max_steps = 3) for xi in x]
yTrue = [np.math.cos(xi) for xi in x]
plt.plot(x, yVals, '_')
plt.plot(x, yVals3, '-')
plt.plot(x, yTrue)

taylor's version2