Skip to content

Latest commit

 

History

History
229 lines (177 loc) · 10.5 KB

안구건조증.md

File metadata and controls

229 lines (177 loc) · 10.5 KB
Raw

Tree

트리는 비선형 계층적 자료구조이다.

  • 비선형 : 하나의 자료 뒤에 여러 개의 자료가 존재할 수 있다.
  • 계층적 : 부모-자식 관계로 서로 연결됨

트리의 구성요소

  • 노드(Node) : 트리를 구성하고 있는 각각의 요소
  • 간선(Edge) : 트리를 구성하기 위해 노드와 노드를 연결하는 선
  • 루트 노드(Root Node) : 트리 구조에서 최상위에 있는 노드
  • 리프 노드(Leaf Node) : 하위에 다른 노드가 연결되어 있지 않은 노드
  • 부모 노드(Parent Node) : 어떤 노드의 다음 레벨에 연결된 노드
  • 자식 노드(Child Node) : 어떤 노드의 상위 레벨에 연결된 노드
  • 형제 노드(Sibling Node) : 같은 부모 노드를 가지는 노드
  • 서브 트리(Sub Tree) : 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
  • 레벨(Level) : 루트 노드부터 해당 노드까지의 경로를 따라 이동할 때 거쳐야 하는 간선의 수
  • 트리의 높이(Height) : 가장 긴 루트 경로의 길이
  • 트리의 깊이(Depth) : 루트 노드 경로까지의 길이
  • 트리의 차수(Degree) : 각 노드의 자식 노드의 개수
  • 트리의 크기(Size) : 트리에 포함된 모든 노드의 개수

왜 트리를 사용하는가?

  • 단순한 비선형적 방식에 비해 데이터 간의 다양한 관계를 표현할 수 있다.
  • 계층적 구조를 가지기 때문에 데이터 간의 관계를 명확히 하고 직관적으로 이해할 수 있다.
  • 데이터의 탐색(검색)에 유리하다. (이진 검색 트리)

Binary Tree (이진 트리)

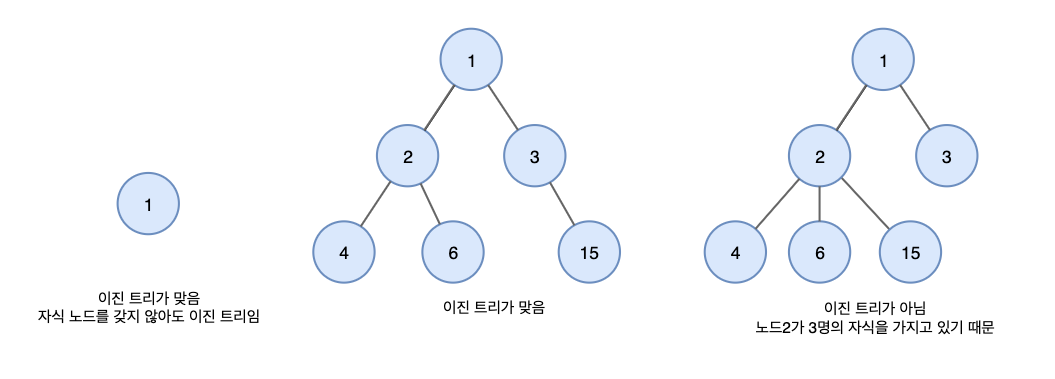
img_1.png 사진 출처 : https://velog.io/@dlgosla/CS-자료구조-이진-트리-Binary-Tree-vzdhb2sp

노드가 최대 두 개의 자식 노드를 가지는 트리 (공집합 포함)

  • 모든 자식 노드들 또한 최대 두 개의 자식 노드를 가질 수 있다.
  • 자식 노드의 위치에 따라 왼쪽 자식 노드와 오른쪽 자식 노드로 구분한다.
  • '최대' 두 개의 자식 노드를 가지기 때문에, 자식 노드가 하나인 경우에도 왼쪽 자식 노드와 오른쪽 자식 노드로 구분한다.

정 이진트리(Full Binary Tree), 완전 이진트리(Complete Binary Tree), 포화 이진트리(Perfect Binary Tree), 균형 이진트리(Balanced Binary Tree) 등의 특수한 형태의 이진 트리가 존재한다.

정 이진 트리(Full Binary Tree)

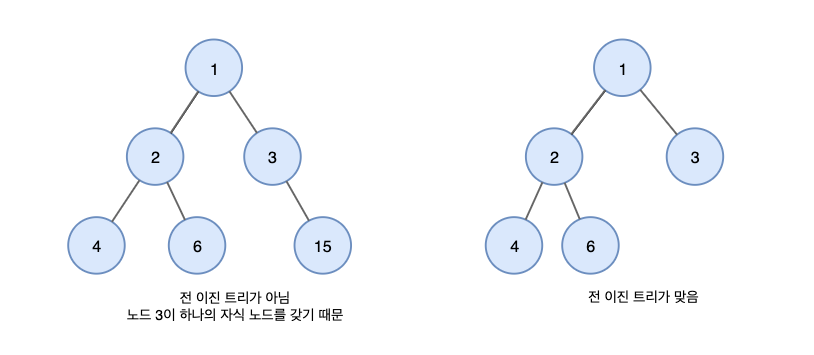
모든 노드가 0개 또는 2개의 자식 노드를 가지는 이진 트리 img_2.png 사진 출처 : https://velog.io/@dlgosla/CS-자료구조-이진-트리-Binary-Tree-vzdhb2sp

장점

  • 구조적 일관성 : 자식 노드의 수가 일정하므로 알고리즘 설계 및 구현에 있어서 예측 가능한 구조를 제공한다.

완전 이진 트리(Complete Binary Tree)

마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 이진 트리 img_3.png 사진 출처 : https://velog.io/@dlgosla/CS-자료구조-이진-트리-Binary-Tree-vzdhb2sp

장점

  • 배열 기반 구현 : 배열을 사용하여 트리를 구현할 수 있어 메모리 사용이 효율적이다.

포화 이진 트리(Perfect Binary Tree)

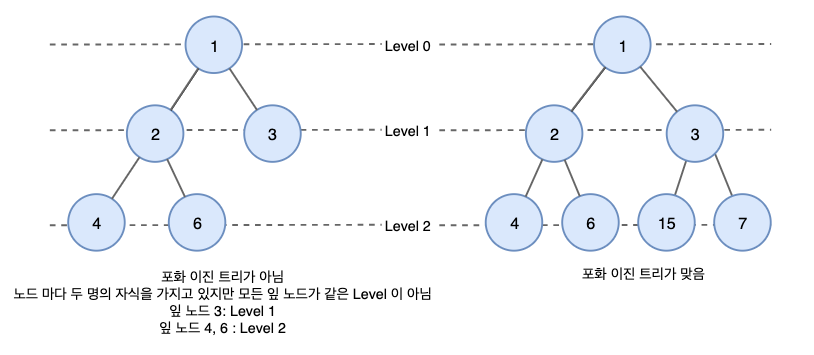
모든 레벨이 완전히 채워져 있는 이진 트리 (정 이진 트리 + 완전 이진 트리) img_4.png 사진 출처 : https://velog.io/@dlgosla/CS-자료구조-이진-트리-Binary-Tree-vzdhb2sp

장점

  • 균형적 구조 : 모든 레벨이 완전히 채워져 있기 때문에 모든 경로의 길이가 균일하게 유지된다. 따라서 최악의 경우에도 예측 가능한 성능을 제공한다.
  • 예측 가능성 : 노드의 개수가 2^k - 1개이므로, 노드의 개수를 알고 있다면 트리의 높이를 알 수 있다. 즉, 탐색 시 트리를 거쳐야 하는 노드의 수가 일정하다. 이는 모든 탐색이 일관된 성능을 보이게 하며, 최의 경우에서도 성능이 갑자기 크게 저하되지 않음을 보장해준다.

BST(Binary Search Tree) (이진 탐색 트리)

이진 탐색 트리는 다음과 같은 속성을 지닌 트리이다.

  • 각 노드에는 하나의 값이 있다.
  • 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
  • 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
  • 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다

img_8.png 사진 출처 : https://ko.wikipedia.org/wiki/이진_탐색_트리

항상 왼쪽 서브트리는 그 노드의 값보다 작은 값이, 오른쪽 서브트리에는 그 노드의 값보다 큰 값을 지니기 때문에, 특정 값을 찾고자 할 때 탐색을 효율적으로 할 수 있다.

단, 이런 효율성은 트리의 균형에 따라 달라진다. 트리가 한쪽으로 치우쳐 있을 경우, 탐색 시간이 O(n)이 될 수도 있다. (예 : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 순서로 삽입할 경우, 1을 루트 노드로 삽입하면 트리는 한쪽으로 치우쳐지게 된다.)

이것을 가리켜 트리가 편향(skew) 되었다고 한다. 이러한 문제를 해결하기 위해 나온 것이 균형 이진 탐색 트리 (Balanced Binary Search Tree) 이다.

Binary Search Tree 구현

import java.util.Scanner;

public class BinSearch {
    //요솟수가 n인 배열 a에서 key와 같은 요소를 이진 검색한다.
    static int BinSearch(int[] a, int n, int key){
        int pl = 0;
        int pr = n - 1;

        do {
            int pc = (pl + pr) / 2;
            
            if (a[pc] == key) return pc; // 일치할 경우 값 리턴
            
            else if (a[pc] < key) pl = pc + 1; // 검색 범위를 뒤쪽 절반으로 좁힘
            
            else {
                pr = pc - 1; // 검색 범위를 앞쪽 절반으로 좁힘
            }
        } while (pl <= pr);

        return -1; // 검색 실패
    }

    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);

        System.out.print("요솟수 : ");
        int num = stdIn.nextInt();
        int[] x = new int[num];

        System.out.println("오름차순으로 입력하세요.");

        System.out.println("x[0] : ");
        x[0] = stdIn.nextInt();

        for(int i = 1; i < num; i++){
            do{
                System.out.print("x[" + i + "] : ");
                x[i] = stdIn.nextInt();
            } while(x[i] < x[i - 1]); //바로 앞의 요소보다 작으면 다시 입력
        }

        System.out.print("검색할 값 : "); // 키 값을 입력
        int ky = stdIn.nextInt();

        int idx = BinSearch(x, num, ky); // 배열 x에서 키 값이 ky인 요소를 출력

        if(idx == -1) System.out.println("그 값의 요소가 없습니다.");
        else System.out.println(ky + "은(는) x[" + idx + "]에 있습니다.");
    }
}

주어진 트리가 BinaryTree인지 확인하는 코드

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
import java.util.Scanner;

public class TreeNode {
    int value;
    List<TreeNode> children;

    TreeNode(int value) {
        this.value = value;
        children = new ArrayList<>();
    }

    void addRandomChildren(int maxChildren, int maxValue) {
        Random random = new Random();
        int childrenCount = random.nextInt(maxChildren + 1);
        System.out.println("생성할 자식 노드 갯수 : " + childrenCount);
        for (int i = 0; i < childrenCount; i++) {
            this.children.add(new TreeNode(random.nextInt(maxValue)));
        }
    }

    static boolean isBinaryTree(TreeNode node) {
        // 공집합일 경우, 이진 트리임
        if (node == null) {
            System.out.println("트리(또는 서브 트리)가 공집합입니다.");
            return true;
        }

        // 자식 노드 갯수가 2개 초과일 시, 이진 트리 아님
        if (node.children.size() > 2) {
            System.out.println("자식 노드의 갯수가 2개를 초과합니다.");
            return false;
        }

        // 자식 노드 재귀 확인
        for (TreeNode child : node.children) {
            if (!isBinaryTree(child)) {
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        // 예제 트리 생성
        TreeNode root = new TreeNode(0); // 루트 노드 생성

        Scanner sc = new Scanner(System.in);
        System.out.println("루트 노드를 제외하고, 노드가 가질 수 있는 자식 노드의 최대 개수를 입력해주세요.");
        int maxChildren = sc.nextInt();

        // 루트 노드 생성
        System.out.println("루트 노드를 생성합니다.");
        root.addRandomChildren(maxChildren, 100); // 최대 maxChildern 만큼의 자식, 값은 0-100

        // 루트 노드 검사
        if (root.children.size() > 2) {
            System.out.println("루트 노드의 자식 노드 갯수가 2개를 초과합니다.");
            System.out.println("이진 트리 여부 : false" );
            return;
        }

        if (root.children.isEmpty()) {
            System.out.println("루트 노드의 자식 노드 갯수가 0개입니다.");
            System.out.println("이진 트리 여부 : true" );
            return;
        }

        // 자식 노드 생성

        int n = 1;
        System.out.printf("%d번 노드의 자식을 생성합니다.\n", n);
        for (TreeNode child : root.children) { // 자식 노드 재귀 생성
            child.addRandomChildren(maxChildren, 100);
            n++;
        }

        // 이진 트리인지 확인
        boolean result = isBinaryTree(root);
        System.out.println("이진 트리 여부 : " + result);
    }
}

면접 예상 질문

  1. 트리(Tree) 자료구조에 대해 설명해주세요.

  2. 이진 트리(Binary Tree)와 일반 트리의 차이점은 무엇인가요?

  3. 이진 탐색 트리(Binary Search Tree, BST)의 주요 속성과 작동 원리를 설명해주세요.

  4. 트리에서 균형을 유지하는 것이 중요한 이유는 무엇인가요?

  5. 트리의 깊이(Depth)와 높이(Height)의 차이점은 무엇인가요?