README.md

50 Important CNN Interview Questions

You can also find all 50 answers here 👉 Devinterview.io - CNN

1. What is a Convolutional Neural Network (CNN)?

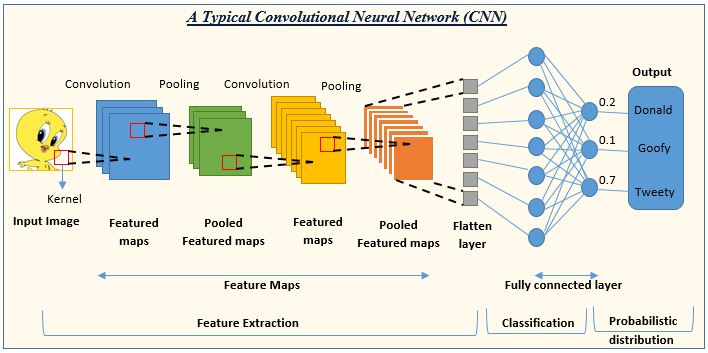
A Convolutional Neural Network (CNN) is a specialized deep-learning system designed to handle visual data by capturing spatial dependencies and hierarchies of features, which are common in images. This model diminishes the requirement for manual feature extraction, making it more efficient than traditional methods such as edge detection and gradient estimation.

Core Components

1. Convolutional Layers: These layers apply convolutional filters to extract features or patterns from the input data.

   • Filter: A small, square matrix that identifies specific features, e.g., edges.
   • Feature Map: The result of applying the filter to the input data.

2. Pooling Layers: These layers reduce spatial dimensions by either taking the maximum value from a group of pixels (max-pooling) or averaging them. This process aids in feature selection and reduces computational load.

3. Fully Connected Layers: Also known as dense layers, they process the output of previous layers to make the final classifications or predictions.

CNN Model Architecture

The typical structure comprises a series of convolutional and pooling layers, followed by one or more dense layers:

• Convolutional-ReLU-Pooling Block: These blocks are stacked to extract increasingly abstract features from the input.

• Fully Connected Layer(s): These layers, placed at the end, leverage the extracted features for accurate classification or regression.

• Output Layer: It provides the final prediction or probability distribution.

Training CNNs

Training a CNN involves:

• Forward Propagation: Data is passed through the network, and predictions are made.

• Backpropagation and Optimization: Errors in predictions are calculated, and the network's parameters (weights and biases) are updated to minimize these errors.

• Loss Function: The magnitude of error in predictions is quantified using a loss function. For classification tasks, cross-entropy is common.

• Optimizer: Techniques such as stochastic gradient descent are used to adjust weights and biases.

Common Activation Functions

• ReLU (Rectified Linear Unit): $f(x) = \max(0, x)$
• Sigmoid: $f(x) = \frac{1}{1 + e^{-x}}$, primarily used in binary classification tasks.
• Softmax: Used in the output layer of multi-class problems, it transforms raw scores to probabilities.

Regularization Techniques

To prevent overfitting, methods such as dropout and L2 regularization are employed:

• Dropout: During training, a fraction of neurons are randomly set to zero, reducing interdependence.
• L2 Regularization: The sum of the squares of all weights is added to the loss function, penalizing large weights.

Advanced Networks

• LeNet: Pioneering CNN designed for digit recognition.
• AlexNet: Famous for winning the ImageNet competition in 2012.
• VGG: Recognized for its uniform architecture and deep layers.
• GoogLeNet (Inception): Noteworthy for its inception modules.
• ResNet: Known for introducing residual connections to tackle the vanishing gradient problem.

Frameworks & Libraries

• TensorFlow: Provides an extensive high-level API, Keras, for quick CNN setup.
• PyTorch: Favored for its dynamic computational graph.
• Keras: A standalone, user-friendly deep learning library for rapid prototyping.

2. Can you explain the structure of a typical CNN architecture?

A standard CNN model is composed of several distinct types of layers that work together to extract features from images and classify them.

Common CNN Layers

1. Convolutional Layer (Conv2D)

   • Responsible for feature extraction
   • Applies a set of learned filters on input data to produce feature maps
   • Implementations such as ReLU/Leaky ReLU introduce non-linearity
   • Just like ReLU, Leaky ReLU helps with vanishing gradients, but also addresses the issue of dead neurons by having a small positive slope for negative values.

2. Pooling Layer

   • Reduces spatial dimensions to control computational complexity
   • Methods include max-pooling and average-pooling
   • Useful for translational invariance

3. Fully-Connected Layer

   • Acts as a traditional multi-layer perceptron (MLP) layer
   • Neurons in this layer are fully connected to all activation units in the previous layer
   • Establishes feature combinatorics across all spatial locations, leading to better understanding of the overall image

4. Dropout layer

   • Regularizes model by reducing the chances of co-adaptation of features
   • During training, it randomly sets a fraction of the input units to 0

5. Flattening Layer

   • Transforms the 3D feature maps from the previous layer into a 1D vector
   • Handles the subsequent input for the fully-connected layer and reduces complexity

6. Batch Normalization Layer

   • Helps stabilize and expedite training by normalizing the input layer by layer

CNN Architecture in Code

Here is the Python code:

import tensorflow as tf
from tensorflow.keras import layers, models

# Initialize the CNN model
model = models.Sequential()

# Add layers to the model
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))

# Compile the model
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# Print model summary
model.summary()

3. How does convolution work in the context of a CNN?

Convolutional Neural Networks (CNNs) use convolutional layers to extract features from input data, which could be images, text, or time series data. Let's look at how convolutional operations are carried out.

Convolutional Operation

The basic idea of convolution in the context of CNNs is to slide a filter/kernel over the input data and perform an element-wise multiplication and summation at each step. This results in a feature map that represents localized patterns in the input data.

Visual Representation

Mathematical Definition

The convolution of a $(n \times n)$ input data matrix $'X'$ with a $(k \times k)$ filter matrix $'F'$ in a single channel operation, which results in an $(m \times m)$ output matrix $'Y'$ can be defined as:

$$ Y(i,j) = \sum_{u=0}^{k-1} \sum_{v=0}^{k-1} X(i+u, j+v) \cdot F(u,v) $$

The filter $'F'$ slides over the input $'X'$ pixel-by-pixel, and at every stop of the sliding filter, the dot product between the filter ($'F'$) and the subset of input data ($X(i:i+k, j:j+k)$) is computed to get the corresponding output.

Practical Application: Feature Extraction

CNNs use the convolution operation to extract features that are then used for the final classification or prediction task:

• In the initial layers, the network might learn simple feature extractors such as edges and corners.
• Deeper layers learn to combine these simple features to recognize more complex patterns like textures and object parts.

Stride and Padding

In the convolutional operation, stride determines the number of positions the filter shifts over the input. It can be any positive integer. If the stride is $s$, The output size will be:

$$ \left\lfloor \frac{n - k}{s} \right\rfloor + 1 $$

For instance, a stride of 2 would shift the filter every two pixels.

Padding adds additional pixels around the input, usually filled with zeros. It's beneficial in retaining the spatial dimensions of the input, especially if the filter size is not evenly divisible by the input size.

Without padding, applying a large filter to the edge of an image might not capture important edge features. With proper padding, the entire edge can be covered.

Pooling Layers

In addition to convolutional layers, CNNs often include pooling layers, which help reduce the spatial dimensions of the input, thereby controlling the number of parameters and computations in the network.

Types of Pooling

• Max Pooling: Selects the maximum pixel value from a region defined by the size of the filter.
• Average Pooling: Takes the average pixel value within the defined region.

4. What is the purpose of pooling in a CNN, and what are the different types?

Pooling in Convolutional Neural Networks $CNNs$ serves the dual purpose of dimensionality reduction and feature extraction.

Pooling Mechanism

The pooling mechanism uses a filter, typically of $2 \times 2$ with a stride of $2$, to scan the input feature map.

• Max Pooling: Selects the maximum value in each window, emphasizing dominant features.
• Average Pooling: Computes the mean of values within the window, offering a smoother response.

Pooling Filter Example

Key benefits of pooling include:

1. Parameter Reduction: By reducing the size of the feature maps, pooling helps minimize the number of neural network parameters, which in turn combats overfitting.

2. Translation Invariance: The pooling process backs the network's resilience to slight positional shifts or translations in the input, which can be valuable for object recognition tasks.

3. Computation Efficiency: Pooling ascends computational efficiency during both training and inference, as it entails a more modest window of operations.

5. How do activation functions play a role in CNNs?

Convolutional Neural Networks (CNNs) are heavily reliant on activation functions to introduce non-linearities, an essential element for learning complex patterns from data.

Why Non-Linearity is Needed

Linear transformations can be represented as $f(x) = Ax + b$, where $A$ is a matrix and $b$ a vector. Without non-linear activations, the entire network would just optimize with respect to this linear transformation.

This is like stacking multiple lines, always resulting in a line, failing to capture complex data distributions typically seen in computer vision tasks.

Role in Filtering and Feature Extraction

The Convolution and Pooling steps in CNNs help identify features in an image. These operations are non-linear and are followed by the application of the activation function.

This combined non-linear operation plays a role in feature extraction such as identifying edges, textures, and more complex patterns like eyes or wheels in a visual scene.

Common Activation Functions in CNNs

1. ReLU (Rectified Linear Unit): $f(x) = \max(0, x)$

   • Benefits: Simple, computationally efficient, and effective at addressing the vanishing gradient problem.
   • Used widely, especially in hidden layers.

2. Sigmoid: $f(x) = \frac{1}{1+e^{-x}}$

   • Outputs a probability, commonly used in binary classification tasks.

3. Tanh: $f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

   • Scaled version of the sigmoid function. Outputs values in the range $(-1, 1)$.

4. Softmax: $f(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{K} e^{x_j}}$

   • Used in multi-class classification problems.
   • Maps multiple output neurons into a probability distribution.

5. Leaky ReLU: $f(x) = x$ for $x > 0$ and $f(x) = ax$ for $x \leq 0$ (where $a$ is a small constant, often 0.01 in practice).

   • A variant of ReLU that allows a small gradient through when the input is negative.

6. ELU (Exponential Linear Unit):

$$ f(x) = \begin{cases} x & x \geq 0 \\ a \times (e^x - 1) & x < 0 \end{cases} $$

• Like Leaky ReLU but smoothly differentiable everywhere.

Code Example

Here is the Python code:

from keras.layers import Activation, Conv2D, MaxPooling2D
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))

6. Can you describe what is meant by 'depth' in a convolutional layer?

In the context of a Convolutional Neural Network (CNN), 'depth' refers to the number of distinct filters applied to the input feature map.

Visual Representation

A 2D filter - essentially a small grid of numbers - processes the input feature map in 2D. When we talk about depth, we are referring to the 'third' dimension denoted by the depth axis in 3D data.

Each filter extends across the entire depth of the input feature map. When you visualize a convolution operation, think of the filter as being 3D, spanning both the height and width of the feature map as well as its depth.

Practical Application

If your input consists of RGB image data, it would have a depth of 3 (one dimension for each of red, green, and blue).

The depth of the filter is usually designed to match the input depth. For instance, in the case of RGB images, it also has a depth of 3.

Consequently, the output of one filter applied to one segment (corresponding to the depth dimension) of the input data results in a single number, just one channel in the output feature map.

The Output after Convolving

When we apply a filter, we convolve it with the input data. Let's assume the input data from the previous layer is $5 \times 5 \times 3$ (meaning a 5x5 2D grid with a depth of 3, which corresponds to, say, our 3 color channels, red, green, and blue).

If we apply ten 3D filters with a size of $3 \times 3 \times 3$, the output of each filter will be a 2D feature map of size $3 \times 3$, and we'll have ten such feature maps.

The entire output of the convolutional layer, in this case, will be a 3D tensor - it's a collection of 2D feature maps, and it will be $3 \times 3 \times 10$. Each depth slice will correspond to the result of convolving the input with one of our 10 filters. Each filter output will be a 2D array with dimensions $3 \times 3$.

Code Example: Depth in Convolutional Layers

Here is the Python code:

from keras.layers import Conv2D
# Creating a 3D Convolutional Layer
conv_layer = Conv2D(filters=10, kernel_size=(3,3), input_shape=(5,5,3), activation='relu')

# Extracting and printing layer details
_, height, width, depth = conv_layer.output_shape
print("Layer Output Dimensions: {}x{}x{}".format(height, width, depth))

7. How do CNNs deal with overfitting?

Convolutional Neural Networks (CNNs) handle overfitting through a combination of techniques that are tailored to their unique architecture, data characteristics, and computational demands.

Techniques to Mitigate Overfitting in CNNs

1. Data Augmentation: Amplifying the dataset by generating synthetic training examples, such as rotated or flipped images, helps to improve model generalization.

2. Dropout: During each training iteration, a random subset of neurons in the network is temporarily removed, minimizing reliance on specific features and enhancing robustness.

3. Regularization: $L_1$ and $L_2$ penalties are used to restrict the size of the model's weights. This discourages extreme weight values, reducing overfitting.

4. Ensemble Methods: Combining predictions from several models reduces the risk of modeling the noise in the dataset.

5. Adaptive Learning Rate: Using strategies like RMSprop or Adam, the learning rate is adjusted for each parameter, ensuring that the model doesn't get stuck in local minima.

6. Early Stopping: The model's training is halted when the accuracy on a validation dataset ceases to improve, an indication that further training would lead to overfitting.

7. Weight Initialization: Starting the model training with thoughtful initial weights ensures that the model doesn't get stuck in undesirable local minima, making training more stable.

8. Batch Normalization: Normalizing the inputs of each layer within a mini-batch can accelerate training and often acts as a form of regularization.

9. Minimum Complexity: Choosing a model complexity that best matches the dataset, as overly complex models are more prone to overfitting.

10. Minimum Convolutional Filter Size: Striking a balance between capturing local features and avoiding excessive computations supports good generalization.

8. What is the difference between a fully connected layer and a convolutional layer?

A Fully-Connected Layer (Dense Layer) and a Convolutional Layer (Convoluted Layer or "ConvLayer") are two key components in convolutional neural networks (CNNs).

Key Distinctions

Local vs. Global Connectivity

• Convolutional Layer: Locally connected, focusing on small regions and sharing weights. Promotes translation invariance.
• Fully-Connected Layer: Globally connected, linking every node in the layer with every node in the previous and following layers. No weight sharing or spatial invariance; instead, it treats each element as distinct.

Weight Sharing

• Convolutional Layer: Shares weights across space, promoting feature detection irrespective of location. This reduces the number of parameters and computational load.
• Fully-Connected Layer: Each connection between layers has a unique weight.

Spatial Awareness

• Convolutional Layer: Preserves the spatial structure of the input image through the use of filters that slide over the width and height of the input.
• Fully-Connected Layer: Does not preserve spatial information. Treats it as a one-dimensional array.

Dimensionality

• Convolutional Layer: Processes multi-dimensional data such as images or sequences.
• Fully-Connected Layer: Acts on flattened multi-dimensional inputs, such as a 1D array obtained from an image or sequence.

Role in CNNs

• Convolutional Layer: Serves as the primary feature extractor from input data, facilitating complex spatial hierarchies.
• Fully-Connected Layer: Acts as the final classifier or regression layer in the network, merging the spatial information extracted by convolutional layers into global decisions.

Visual Comparison

Convolutional Layers

A Convolutional layer operates on a multi-dimensional input, like an image, with learned filters or kernels that slide over the input, producing feature maps.

Fully-Connected Layers

A fully connected layer treats the input as a flattened 1D array, with all neurons interconnected through learned weights, carrying out the final classification or regression task.

9. What is feature mapping in CNNs?

In Convolutional Neural Networks (CNNs), Feature Mapping refers to the process of transforming the input image or feature map into higher-level abstractions. It strategically uses filters and activation functions to identify and enhance visual patterns.

Importance of Feature Mapping

Feature mapping performs two key functions:

1. Feature Extraction: Through carefully designed filters, it identifies visual characteristics like edges, corners, and textures that are essential for the interpretation of the image.

2. Feature Localization: By highlighting specific areas of the image (for instance, the presence of an edge or a texture), it helps the network understand the spatial layout and object relationships.

Convolutional Layers: The Key Element

Feature mapping typically takes place in convolutional layers, which are the fundamental building blocks of a CNN.

Each neuron in a convolutional layer is associated with a small, local region of the input volume, called the receptive field. This neuron computes a weighted sum of the activations within its receptive field, producing a single value in the output feature map.

Process Flow in Convolutional Layers

1. Convolution: The layer performs a 2D convolution operation, sliding a small filter (kernel) over the input feature map to produce an output feature map. This process enables local connectivity, meaning each neuron is connected only to a subset of the input.

2. Non-linearity: Following the convolution, a non-linear activation function, such as ReLU, is applied element-wise to introduce non-linearity to the model.

3. Pooling: Subsampling through operations like max-pooling reduces the spatial dimensions of the feature maps, leading to dimensionality reduction. This step is crucial for reducing the model's parameter count and helping it focus on the most salient features.

Concept Validation: Real-World Filters

Filter Types

• Edge Detector: Recognizes changes in pixel intensity which indicate edges.
• Blur Filter: Averages pixels to create a blurred effect.
• Sharpening: Enhances edges.

The Role of Bias in Feature Mapping

In CNNs, bias is a learnable parameter associated with each filter, independent of the input data. Bias adds flexibility to the model, enabling it to better represent the underlying data.

Compute Formula with Bias

$$y = \sigma(W \ast x + b)$$

where:

• $W$ is the filter weight.
• $\ast$ denotes the convolution operation.
• $x$ is the input.
• $b$ is the bias term.
• $\sigma$ is the activation function (e.g., ReLU).

Code Example: Feature Mapping and Bias

Here is the Python code:

import numpy as np
import tensorflow as tf

# Create input data (assumed to be a 3x3 grayscale image for simplicity)
x = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
], dtype=np.float32)

# Reshape input for compatibility with TensorFlow
x = x.reshape(1, 3, 3, 1)

# Create a 2x2 filter for edge detection (Sobel filter)
filter_weights = np.array([
    [[-1., 0.],
     [-2., 0.]]
])
filter_weights = np.transpose(filter_weights, [1, 2, 0, 0])  # Reshape for TensorFlow

# Define the bias term for the filter
filter_bias = np.array([1.0])

# Convert the filter weights and bias to TensorFlow variables
W = tf.Variable(filter_weights, dtype=tf.float32)
b = tf.Variable(filter_bias, dtype=tf.float32)

# Perform the convolution with bias
conv_result = tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='VALID') + b

# Apply ReLU activation
output = tf.nn.relu(conv_result)

# Initialize TensorFlow variables and run the session
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    result = sess.run(output)
    print("Output Feature Map with Bias:\n", result)

10. How does parameter sharing work in convolutional layers?

Parameter sharing is a fundamental aspect of Convolutional Neural Networks (CNN).

Core Mechanism: Reducing Overfitting and Computational Costs

Parameter sharing minimizes overfitting and computational demands by using the same set of weights across different receptive fields in the input.

• Overfitting Reduction: Sharing parameters helps prevent models from learning noise or specific features that might be unique to certain areas or examples in the dataset.

• Computational Efficiency: By reusing weights during convolutions, CNNs significantly reduce the number of parameters to learn, leading to more efficient training and inference.

Practical Implementation

Shared parameters in CNNs are established by using convolutional kernels (also called filters):

• A 1D kernel is essentially a single parameter, i.e., one weight.
• For a 2D kernel, each unique position corresponds to one parameter, and the kernel's dimensions determine the number of parameters.
• Analogous to 2D kernels, 3D kernels provide parameter sharing in 3D convolutions.
• Recent developments showcase the use of hypercolumns and frustum-based convolutions for fine-grained feature extraction.

Parameter Sharing and Weight Tying

In CNNs, parameter sharing ensures that the same weights are used across different input regions. Moreover, in some CNN architectures, weight tying takes this a step further where the same weights are used across layers. Variants include input-to-state, state-to-state, and output-to-output weight tying.

For instance, in Recurrent and Auto-Regressive models:

• RNNs: The same weights are employed at each timestep, ensuring that past information is leveraged consistently across the sequence.

• LSTMs: They extend parameter sharing to memory cells, regulating the flow of cell state information across time and alongside other input modulators, such as input and forget gates.

• GRUs: Introduce combined memory and forget gate units that are regulated by the same weights.

Auto-Regressive models, popular in time series and sequence tasks, iterate over their own predictions - generally one step at a time - to produce sequences. By sharing weights, these models can effectively exploit a unifying set of parameters for this tasks.

Unfolding the Mechanism: Reconstruction and Activation

Using CNNs, we can understand how convolutional transformations unfold, effecting reconstruction and activation of the input data:

1. Linear Transform: The input data matrix is linearly transformed, using pointwise products, with the kernel weights to generate a feature map.

   $$F[i, j] = \sum_m ∑_n I[i+m, j+n] * K[m, n] $$

2. Receptive Field Normalization: Input data within the receptive field is segmented and normed, and the normalized segments are pointwise multiplied with the kernel. Variants of normalizations include L1 and L2 norm.

3. Activation: The convolutional output (pre-activation) can be passed through a non-linear activation function to introduce complex, non-linear representations in the data.

   $$ A[i, j] = \sigma(F[i, j]) $$

4. Pooling and Stride Reduction: Through pooling and stride functions, the feature map is either compressed or spatially reduced. Pooling functions common to CNNs include max-pooling and average pooling.

11. Why are CNNs particularly well-suited for image recognition tasks?

Convolutional Neural Networks (CNNs) are optimized for image recognition. They efficiently handle visual data by leveraging convolutional layers, pooling, and other architectural elements tailored to image-specific features.

Image-Centric Features of CNNs

• Weight Sharing: CNNs utilize the same set of weights across the entire input (image), which is especially beneficial for grid-like data such as images.
• Local Receptive Fields: By processing input data in small, overlapping sections, CNNs are adept at recognizing local patterns.

Convolution and Pooling: Advantages for Image Data

Convolutional Layers apply a set of filters to the input image, identifying features like edges, textures, and shapes. This process is often combined with pooling layers that reduce spatial dimensions, retaining pertinent features while reducing the computational burden.

Pooling makes CNNs robust to shifts in the input, noise, and variation in the appearance of detected features.

Visual Intuition: Convolution and Pooling

• Convolution: Imagine a filter sliding over an image, detecting features in a localized manner.
• Pooling: Visualize a partitioned grid of the image. The max operation captures the most important feature from each grid section, condensing the data.

Code Example: Convolution and Max Pooling

Here is the Python code:

# Sample CNN with convolution and max pooling layers
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense

# Initialize the CNN
classifier = Sequential()

# Add a 2D convolutional layer
classifier.add(Conv2D(32, (3, 3), input_shape=(64, 64, 3), activation='relu'))

# Add max pooling
classifier.add(MaxPooling2D(pool_size=(2, 2)))

# Flatten the output prior to the fully connected layers
classifier.add(Flatten())

# Add the fully connected layers
classifier.add(Dense(units=128, activation='relu'))
classifier.add(Dense(units=1, activation='sigmoid'))

classifier.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

12. Explain the concept of receptive fields in the context of CNNs.

Receptive fields in the context of Convolutional Neural Networks (CNNs) refer to the area of an input volume that a particular layer is "looking" at. The receptive field size dictates which portions of the input volume contribute to the computation of a given activation.

Local Receptive Fields

The concept of local receptive fields lies at the core of CNNs. Neurons in a convolutional layer are connected to a small region of the input, rather than being globally connected. During convolution, the weights in the filter are multiplied with the input values located within this local receptive field.

Pooling and Subsampling

Pooling operations are often interspersed between convolutional layers to reduce the spatial dimensions of the representation. Both max-pooling and average-pooling use a sliding window over the input feature map, sliding typically by the same stride value as the corresponding convolutional layer.

Additionally, subsampling layers shrink the input space, typically by discarding every nth pixel and are largely phased out for practical applications.

Role in Feature Learning

Receptive fields play a crucial role in learning hierarchical representations of visual data.

In early layers, neurons extract simple features from local input regions. As we move deeper into the network, neurons have larger receptive fields, allowing them to combine more complex local features from the previous layer.

This stratification of receptive fields enables the network to construct representations in which higher-level neurons are sensitive to more abstract and global image properties.

Code Example: Calculating Receptive Fields

Here is the Python code:

def output_size(input_size, kernel_size, stride, padding=0):
    return ((input_size - kernel_size + 2 * padding) / stride) + 1

input_size = 32
kernel_size = 3
stride = 1
padding = 1

# Calculate output size of first convolutional layer
output_size_1 = output_size(input_size, kernel_size, stride, padding)
print("Output size of first convolutional layer:", output_size_1)

# Calculate output size of second convolutional layer
kernel_size = 3
stride = 2
padding = 0
output_size_2 = output_size(output_size_1, kernel_size, stride, padding)
print("Output size of second convolutional layer:", output_size_2)

13. What is local response normalization, and why might it be used in a CNN?

Local Response Normalization (LRN) was originally proposed for AlexNet, the CNN that won the 2012 ImageNet Challenge. However, the technique has mostly been superseded by others like batch and layer normalization.

Mechanism

LRN computes normalized activations in a local $n \times n$ neighborhood for each feature map. This process using the formula:

$$ B_{x,y}^{i} = \frac{A_{x,y}^{i}}{\left( k + \alpha \sum_{j=\max(0,i-n/2)}^{\min(N-1,i+n/2)} (A_{x,y}^j)^2 \right)^{\beta} } $$

where:

• $B_{x,y}^{i}$ is the normalized activation of the $i$th feature map at position $(x,y)$.
• $A_{x,y}^{i}$ is the original activation.
• $N$ is the number of feature maps.
• $n$ is the size of the normalization window.
• $k, \alpha, \text{and} , \beta$ are hyperparameters.

Advantages

• Improved Detectability: By enhancing the activations of "strong" cells relative to their neighbors, LRN can lead to better feature responses.
• Implicit Feature Integration: The technique can promote feature map cooperation, making the CNN more robust and comprehensive in its learned representations.

Disadvantages

• Lack of Widespread Adoption: The reduced popularity of LRN in modern architectures and benchmarks makes it a non-standard choice. Moreover, implementing LRN across different frameworks can be challenging, leading to its disuse in production networks.

• Redundancy with Other Normalization Methods: More advanced normalization techniques like batch and layer normalization have shown similar performance without being locally limited.

When to Consider LRN

Due to its limited application, LRN is best-suited for specialized cases where using more conventional normalization techniques isn't feasible or detrimentally affects model performance, which may be rare.

It might interest researchers and experimenters, especially those exploring historical CNN architectures like AlexNet, to see how modifying normalization techniques impacts network behavior and performance.

14. Can you explain what a stride is and how it affects the output size of the convolution layer?

In a convolutional neural network, 'stride' is the number of pixels by which the kernel moves as it sweeps across the input. This parameter influences the size of the output feature map.

Stride and Output Size

The dimensionality of the output of a convolutional layer is determined by the following equation:

• $W_{out} = \frac{W_{in} - F + 2P}{S} + 1$
• $H_{out} = \frac{H_{in} - F + 2P}{S} + 1$

where:

• $F$ is the filter size (width and height usually equal).
• $S$ is the stride.
• $P$ is the amount of zero-padding used.
• $W_{in}$ and $H_{in}$ are the width and height of the input.

The formula shows that:

• No striding ($S = 1$): Every adjacent field (defined by the filter) in the input is assessed.
• Striding $S &gt; 1$ means that fewer fields in the input are considered, thus reducing the output size.

Example: Image with One Channel and Two Features

Let's consider a grayscale image as the input to a convolutional layer with only $\text{one feature}$ ($1 \times 1 \times 2$):

$$ \text{Input}: \begin{pmatrix} 1 & 3 \ 1 & 1 \end{pmatrix} $$

We'll use a $2 \times 2$ filter, no padding, and two different stride values of 1 and 2 to find the $\text{Output}$ feature maps.

Stride = 1

Using stride $S = 1$, the output feature map will be:

$$ \begin{pmatrix} -2 & 2 \ -2 & 0 \end{pmatrix} $$

By applying the formula for height and width, the output values are:

$$ W_{out} = \frac{2 - 2 + 2 \cdot 0}{1} + 1 = 2, \quad H_{out} = 2 $$

Stride = 2

With a stride of 2 ($S = 2$), the output image and size are:

$$ \text{Output}: \begin{pmatrix} -2 \end{pmatrix}, \quad W_{out} = \frac{2 - 2 + 2 \cdot 0}{2} + 1 = 1, \quad H_{out} = 1 $$

15. How do dilated convolutions differ from regular convolutions?

Dilated convolutions, also known as atrous convolutions, offer a unique alternative to traditional convolutions, especially advantageous for CNNs with large receptive fields.

How Do They Differ?

Dilated convolutions differ from traditional ones in these key aspects:

1. Filter Application: While regular convolutions apply the filter to all spatial dimensions, dilated convolutions skip some dimensions, yielding sparse feature maps.

2. Field-of-View Expansion: Dilated convolutions achieve a wider receptive field without using larger filter sizes. This expansion is controlled by the dilation rate.

Understanding Dilation Rates

The dilation rate, denoted as $d$, indicates the spacing between filter weights while applied on the feature map. A dilation rate of 1 corresponds to the standard convolution, with all adjacent pixels being evaluated.

Visualize how the dilation rate affects filter weights placement:

Dilation Rate = 1	Dilation Rate = 2

The Impact of Dilation

• Receptive Field Enlargement: Using dilated convolutions allows for a larger effective receptive field, making these convolutions effective for tasks that require long-range dependencies.
• Data Sparsity: The sparsity introduced by dilated convolutions can be beneficial in tasks like contour detection in images or generating music with deep learning techniques, auto-regressive models, or WaveNet.

Use Cases in CNN Architectures

• Image Segmentation: Dilated convolutions are used in the encoder-decoder model to provide detailed segmentations.
• WaveNet: This speech synthesis model adopts dilated convolutions to capture context in high-resolution audio waveforms.
• ASPP: The Atrous Spatial Pyramid Pooling module in models such as DeepLab for semantic segmentation utilizes dilated convolutions at multiple rates to ensure a broad context for classification.

Code Example: Dilated Convolutions

Here is the Python code:

# Importing necessary libraries
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Conv2D

# Defining the input
input_data = np.array([[
    [1, 2, 3, 4, 5, 6, 7, 8],
    [9, 10, 11, 12, 13, 14, 15, 16],
    [17, 18, 19, 20, 21, 22, 23, 24],
    [25, 26, 27, 28, 29, 30, 31, 32],
    [33, 34, 35, 36, 37, 38, 39, 40],
    [41, 42, 43, 44, 45, 46, 47, 48],
    [49, 50, 51, 52, 53, 54, 55, 56],
    [57, 58, 59, 60, 61, 62, 63, 64]
]])

# Setting up dilated convolution in Keras
dilated_conv = Conv2D(filters=1, kernel_size=3, dilation_rate=2, use_bias=False)

# Using the dilated convolution on the input data
output_data = dilated_conv(input_data)

# Displaying results
print("Original Input:\n", input_data)
print("Output after Dilated Convolution:\n", output_data)

Explore all 50 answers here 👉 Devinterview.io - CNN