给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
- 1.对于该题的最近的公共祖先定义:对于有根树T的两个结点
p、q,最近公共祖先LCA(T,p,q)表示一个结点x,满足x是p和q的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先. - 2.二叉搜索树是若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 3.所有节点的值都是唯一的。
- 4.
p、q为不同节点且均存在于给定的二叉搜索树中。
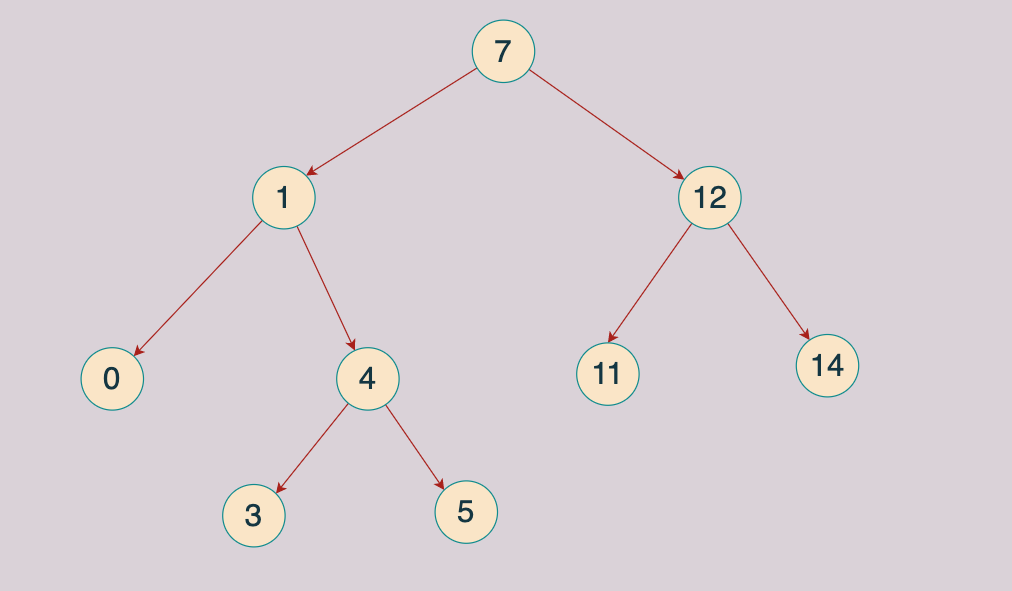
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5},如下图:
示例 1
输入: {7,1,12,0,4,11,14,#,#,3,5},1,12
输出: 7
说明:
节点1 和 节点12的最近公共祖先是7
示例 2
输入: {7,1,12,0,4,11,14,#,#,3,5},12,11
输出: 12
说明:因为一个节点也可以是它自己的祖先.所以输出12
何为二叉树查找树?
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
也就是像下面这个:
题目已经保证了,两个节点 p,q 都在树上,我们取出根节点 7 ,假设小于 7 ,则在左子树,如果大于 7 ,则在右子树。
那么需要查找的两个节点,但凡有一个等于根节点,它们的父节点就是根节点,因为一个节点的父节点可以是自身(题目有说明)。
如果一个大于根节点,一个小于更节点,其最近公共祖先也是根节点。
如果两个都大于,或者两个都小于,怎么办?
当然是递归,如果两个都小于,那么就取当前的左子树进行递归,直到符合要求。比如查找,3 和 5,由于 3 和 5 都小于 7,那么取左子树 1 下面的进行递归:
Java 代码如下:
class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public class Solution68 {
public int lowestCommonAncestor(TreeNode root, int p, int q) {
TreeNode result = commonAncestor(root, p, q);
return result == null ? -1 : result.val;
}
public TreeNode commonAncestor(TreeNode root, int p, int q) {
// 等于空
if (root == null) {
return null;
}
if (root.val == p || root.val == q) {
// 有一个值等于根节点
return root;
}
// 在左子树
if (p < root.val && q < root.val) {
return commonAncestor(root.left, p, q);
} else if (p > root.val && q > root.val) {
// 两个都在右子树
return commonAncestor(root.right, p, q);
} else {
return root;
}
}
}C++ 代码如下:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
int lowestCommonAncestor(TreeNode *root, int p, int q) {
TreeNode *result = commonAncestor(root, p, q);
return result == NULL ? -1 : result->val;
}
TreeNode *commonAncestor(TreeNode *root, int p, int q) {
// 等于空
if (root == NULL) {
return NULL;
}
if (root->val == p || root->val == q) {
// 有一个值等于根节点
return root;
}
// 在左子树
if (p < root->val && q < root->val) {
return commonAncestor(root->left, p, q);
} else if (p > root->val && q > root->val) {
// 两个都在右子树
return commonAncestor(root->right, p, q);
} else {
return root;
}
}
};假设这道题条件改一下,如果不是二叉搜索树,怎么办?
如果不是二叉搜索树,那么我们不能直接判断出它在左子树,还是在右子树。不如暴力点,先在左子树中找,如果右子树没找到,说明都在左子树,如果左子树没找到,说明都在右子树,如果两个都分别存在,说明当前节点就是他们的父节点。
Java 代码如下:
public class Solution68 {
public int lowestCommonAncestor(TreeNode root, int p, int q) {
TreeNode result = commonAncestor(root, p, q);
return result == null ? -1 : result.val;
}
public TreeNode commonAncestor(TreeNode root, int p, int q) {
if (null == root) {
return null;
}
if (root.val == p || root.val == q) {
return root;
}
TreeNode left = commonAncestor(root.left, p, q);
TreeNode right = commonAncestor(root.right, p, q);
if (left == null) {
return right;
} else if (right == null) {
return left;
} else {
return root;
}
}
}C++ 代码如下:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
int lowestCommonAncestor(TreeNode *root, int p, int q) {
TreeNode *result = commonAncestor(root, p, q);
return result == NULL ? -1 : result->val;
}
TreeNode *commonAncestor(TreeNode *root, int p, int q) {
// 等于空
if (root == NULL) {
return NULL;
}
if (root->val == p || root->val == q) {
// 有一个值等于根节点
return root;
}
TreeNode* left = commonAncestor(root->left, p, q);
TreeNode* right = commonAncestor(root->right, p, q);
if (left == NULL) {
return right;
} else if (right == NULL) {
return left;
} else {
return root;
}
}
};