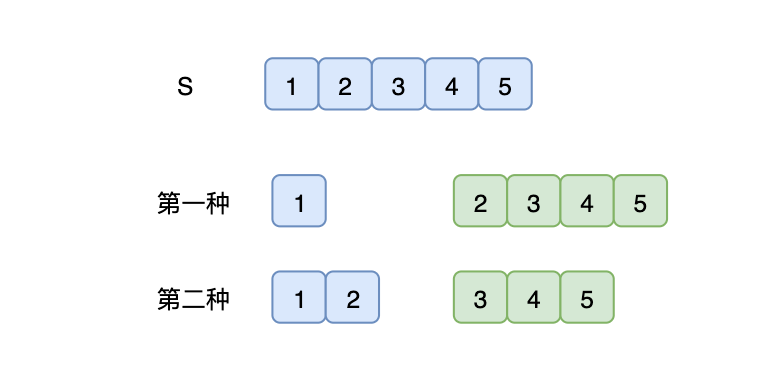
有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。
现在给一串数字,返回有多少种可能的译码结果
示例1
输入:"12"
返回值:2
说明:
2种可能的译码结果(”ab” 或”l”) 示例2
输入:"31717126241541717"
返回值:192
说明:
192种可能的译码结果 仔细观察,就会发现上面的编码从 1 到 26,也就是可能一次译码使用是 1 位,也可能是一次译码用了 2 位,比如 12 ,可以第一次用 1,2 分开分别译码,也可以把 1,2 合并起来进行译码。
假设一个字符是S,第一次拆解就有两种情况,然后分别对后面的部分分别译码,使用递归即可:
Java 代码实现如下:
public class Solution46 {
public int solve (String nums) {
return recursion(nums.toCharArray(), 0);
}
public int recursion(char[] nums, int start){
if(start == nums.length){
return 1;
}
if(nums[start] == '0')
return 0;
// 使用一位字符译码
int count1 = recursion(nums,start+1);
int count2 = 0;
// 符合两位字符的译码
if((start < nums.length-1)
&& (nums[start] == '1' || (nums[start] == '2' &&nums[start+1] <= '6'))){
count2 = recursion(nums,start+2);
}
return count1 + count2;
}
}C++ 代码实现如下:
class Solution {
public:
int solve(string nums) {
return recursion(nums, 0);
}
int recursion(string nums, int start) {
if (start == nums.size()) {
return 1;
}
if (nums[start] == '0')
return 0;
// 使用一位字符译码
int count1 = recursion(nums, start + 1);
int count2 = 0;
// 符合两位字符的译码
if ((start < nums.size() - 1)
&& (nums[start] == '1' || (nums[start] == '2' && nums[start + 1] <= '6'))) {
count2 = recursion(nums, start + 2);
}
return count1 + count2;
}
};但是上面的代码时间复杂度太高了,只要字符稍微长一点,运行时间就超过限制了:
这道题其实可以用动态规划,为什么这么说?
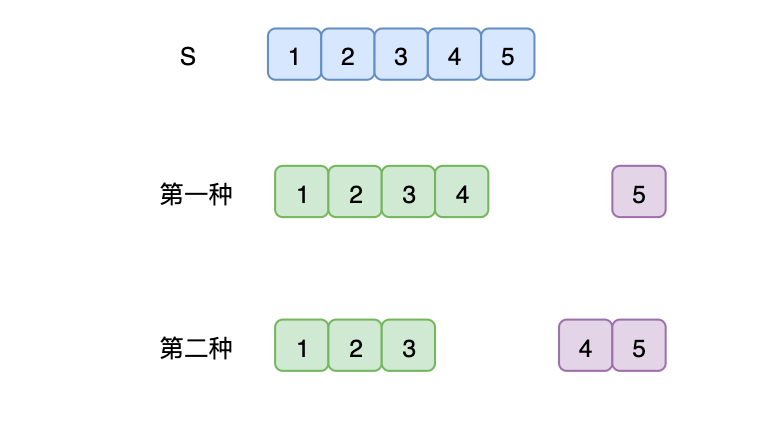
我们将过程逆推,要想求得当前的字符串的译码类型,其实有两种,最后一个单独翻译,另外一种是倒数最后两个字符合起来翻译,这两者之和就是我们所要求的结果。
而要求前面的值,需要求更前面的值,最后一定会求得一个字符和两个字符的结果。其实这就是动态规划里面说的状态变化。递归其实就是逆推,这样会导致很多重复的计算。动态规划,则是从小数值计算到大数值。
既然我们知道是动态规划,定义dp[i]为数字串从左到右第i个数字结尾的当前数字串所拥有的翻译方法数,接着就需要找出状态转移方程:
- 如果
i=0,dp[i]=1 - 否则
- 如果nums[i]=0,说明需要和前面一个字符一起翻译
- 如果i==1,以以10或者20开头,
dp[i] = 1 - 否则,数字串中存在10或者20的情况下,当前译码数等于后退两步的译码数,
dp[i] = dp[i-2];
- 如果i==1,以以10或者20开头,
- 否则,在符合字符范围内,
dp[i]=dp[i-1]+dp[i-2]
- 如果nums[i]=0,说明需要和前面一个字符一起翻译
Java 代码实现如下:
import java.util.*;
public class Solution {
/**
* 解码
* @param nums string字符串 数字串
* @return int整型
*/
public int solve(String nums) {
int len = nums.length();
if (len == 0 || nums.charAt(0) == '0')
return 0;
int[] dp = new int[len];
dp[0] = 1;
for (int i = 1; i < len; i++) {
if (nums.charAt(i) == '0') {
if (nums.charAt(i - 1) == '1' || nums.charAt(i - 1) == '2') {
if (i == 1) {
dp[i] = 1;
} else {
dp[i] = dp[i - 2];
}
}
} else if (nums.charAt(i - 1) == '1'
|| (nums.charAt(i - 1) == '2' && nums.charAt(i) >= '1' && nums.charAt(i) <= '6')) {
if (i == 1) {
dp[i] = 2;
} else {
dp[i] = dp[i - 1] + dp[i - 2];
}
} else {
dp[i] = dp[i - 1];
}
}
return dp[len - 1];
}
}C++ 代码如下:
class Solution {
public:
int solve(string nums) {
int len = nums.size();
if (len == 0 || nums[0] == '0')
return 0;
vector<int> dp(len, 0);
dp[0] = 1;
for (int i = 1; i < len; i++) {
if (nums[i] == '0') {
if (nums[i - 1] == '1' || nums[i - 1] == '2') {
if (i == 1) {
dp[i] = 1;
} else {
dp[i] = dp[i - 2];
}
}
} else if (nums[i - 1] == '1'
|| (nums[i - 1] == '2' && nums[i] >= '1' && nums[i] <= '6')) {
if (i == 1) {
dp[i] = 2;
} else {
dp[i] = dp[i - 1] + dp[i - 2];
}
} else {
dp[i] = dp[i - 1];
}
}
return dp[len - 1];
}
};时间复杂度: 遍历计算所有的数组,O(n)
空间复杂度:使用额外的数组保存计算结果,因此空间复杂度为O(n)