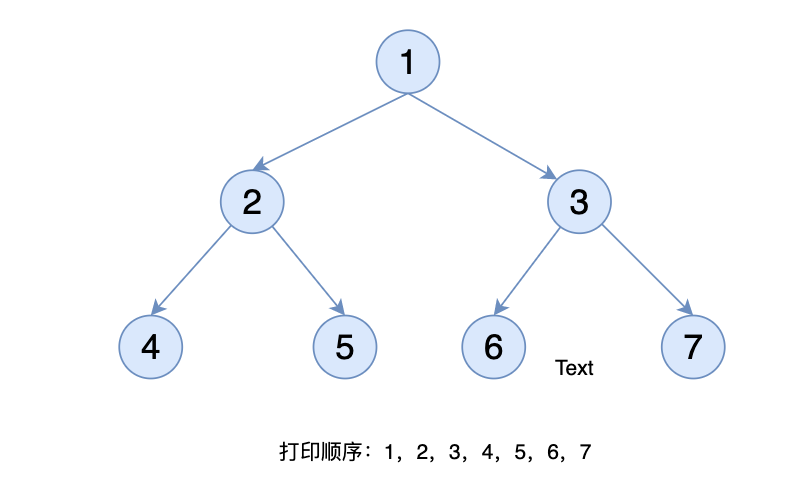
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
主要的思路是借助队列,先把当前元素放进队列,然后不断取出元素,取出元素的时候,同时处理其左子树和右子树,将其放到队列中。直到队列是空的。
众所周知,队列的特点是先进先出,也就是我们可以保证,根节点先进去,然后根节点取出来,打印根节点,同时如果根节点的左节点不为空,则将左节点放进去队列,右节点如果不为空,同样放进去队列中,然后又取出队列的第一个元素,打印,将它的左右节点不为空的加到队列中,这样循环下去即可...
PS:LinkedList是双向队列,queue.add()是在队列后面添加元素,queue.pollFirst()是将第一个元素取出队列。
Java 实现代码如下:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> results = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
if (root != null) {
queue.add(root);
while (!queue.isEmpty()) {
TreeNode treeNode = ((LinkedList<TreeNode>) queue).pollFirst();
results.add(treeNode.val);
if(treeNode.left!=null){
((LinkedList<TreeNode>) queue).add(treeNode.left);
}
if(treeNode.right!=null){
((LinkedList<TreeNode>) queue).add(treeNode.right);
}
}
}
return results;
}
}C++ 代码实现如下:
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode *root) {
vector<int> results;
deque<TreeNode *> myQueue;
if (root != NULL) {
myQueue.push_back(root);
while (myQueue.size()>0) {
TreeNode *treeNode = myQueue.front();
myQueue.pop_front();
results.push_back(treeNode->val);
if (treeNode->left != NULL) {
myQueue.push_back(treeNode->left);
}
if (treeNode->right != NULL) {
myQueue.push_back(treeNode->right);
}
}
}
return results;
}
};- 时间复杂度:O(n),二叉树的每个节点都遍历一次
- 空间复杂度:O(n),二叉树的每个节点入队列一次