23.链表中环的入口结点.md

23.链表中环的入口节点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

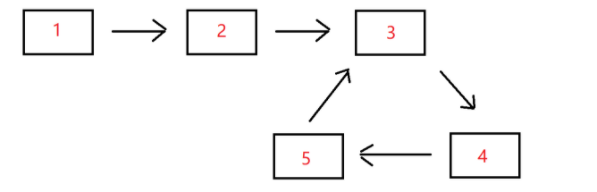
例如，输入{1,2},{3,4,5}时，对应的环形链表如下图所示：

可以看到环的入口结点的结点值为3，所以返回结点值为3的结点。

给定的链表节点的结构：

 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}

思路 & 解答

第一种是直接使用 HashSet,遍历链表的时候，如果 HashSet 中不包含，则添加到 HashSet中，如果链表中包含，说明已经回到环的第一个节点。Java代码实现如下：

    public ListNode EntryNodeOfLoop(ListNode pHead) {
        HashSet set = new HashSet();
        while(pHead!=null){
            if(set.contains(pHead)){
                return pHead;
            }else{
                set.add(pHead);
                pHead = pHead.next;
            }
        }
        return null;
    }

C++ 代码实现如下：

class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        unordered_set<listnode*> myset;
        while (pHead) {
            if (myset.find(pHead) == myset.end()) {
                myset.insert(pHead);
                pHead = pHead->next;
            }
            else {
                return pHead;
            }
        }
        return NULL;
    }
};

当然，上面的做法时间复杂度为O(n)，由于借助了一个hashSet，空间复杂度也为O(n)。

那假设我们不需要使用额外的空间呢？怎么做呢？

使用快慢双指针，一个一次走一步，一个一次走两步,当两个重合在一起的时候，这时候，并不是环的入口节点。只能说明两个指针，一个比另外一个多走了若干圈，可能是一圈，可能是2，3圈。

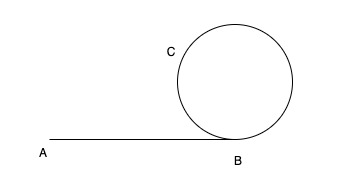
比如上面的，如果开始节点是A，环的入口是B，相遇的节点是C，那么慢指针走的应该是：S= AB+BC

快指针走的是：2S = AB+(BC+CB)*n+BC，假设多走了n圈

2(AB+BC) = AB+(BC+CB)*n+BC

AB+BC = (BC+CB)*n

假设n =1，那么AB = CB,也就是当前位置到环的入口的长度，等于链表头到环的入口的位置。

因此相遇之后，我们讲一个快指针移动到链表头，两个指针每次一步，直到相遇，这个时候，相遇的节点就是换的入口节点。

Java 实现如下：

    public ListNode EntryNodeOfLoop(ListNode pHead) {
        ListNode quick = pHead;
        ListNode slow = pHead;
        while (quick != null && slow.next != null) {
            quick = quick.next;
            slow = slow.next.next;
            if (quick == slow) {
                quick = pHead;
                while (quick != slow) {
                    quick = quick.next;
                    slow = slow.next;
                }
                return quick;
            }
        }
        return null;
    }

C++ 代码实现如下：

class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        ListNode *quick = pHead;
        ListNode *slow = pHead;
        while (quick != NULL && slow->next != NULL) {
            quick = quick->next;
            slow = slow->next->next;
            if (quick == slow) {
                quick = pHead;
                while (quick != slow) {
                    quick = quick->next;
                    slow = slow->next;
                }
                return quick;
            }
        }
        return NULL;
    }
};

时间复杂度：O(n) 空间复杂度：O(1)